四角锥台形人工鱼礁斜面倾角变化对流场效应的影响
2022-07-02吕泽砚朱文斌唐伟尧管青龙刘莉莉张纹瑄傅鑫洋
吕泽砚,朱文斌,唐伟尧,管青龙,刘莉莉,张纹瑄,傅鑫洋
(浙江海洋大学水产学院,浙江舟山 316022)
人工鱼礁是人工投放于海底的渔业工程设施,可以有效地吸引鱼群,为鱼类提供适宜栖居、繁殖及躲避敌害的场所,从而有效地增殖鱼类,养护渔业资源,提高渔业资源修复效率,改善水域生态环境[1-5]。许多沿海国家建立专门的组织,系统地实施沿海渔业修复工程项目,并加大人工鱼礁的科学研究和开发投入。
由于人工鱼礁的投放可以改变海域局部流场,所产生的上升流及涡流的影响可以改变沉积物中营养物质在水域中的分布[6-10]。因此,在人工鱼礁流场效应研究过程中,掌握其周围流态的变化尤为关键。目前,关于人工鱼礁的流场效应研究主要分为数值模拟与模型试验,数值模拟主要集中在对不同结构特性和不同工况下人工鱼礁所在的海域流场分布进行分析,而模型试验主要分为水槽试验[11-13]、PIV 模型试验等。刘洪生等[14]和李珺等[15]借助水槽实验,验证了人工鱼礁流场效应数值模拟研究的可行性;随着数值模拟技术在人工鱼礁流场效应研究的深入,在礁体开孔情况[16-19]、礁体形状[20-22]、礁体布设间距[23]、投放个数与组合方式[24-26]等诸要素对人工礁体流场效应的影响研究方面,取得了一定进展。其中单个礁体的研究均表明礁体形状的变化对绕流情况有显著影响。
人工鱼礁的设计需要同时考虑流场效应以及造礁材料的成本问题。鱼礁按外观可分为正方体形、多面体形、锥形、圆筒形、半圆形等多种形状,对锥形鱼礁而言,倾斜角是影响鱼礁周围流场的因素之一,不同的倾斜角会对上升流效应及流场变化有较大影响。当前,国内关于不同倾斜角情况下的鱼礁流场效应研究未见报道。因此,本研究以四角锥台形鱼礁为例,在保持鱼礁等底等高的情况下,预设5 种不同的斜面倾角,建立计算流体动力学(CFD)模型,通过有限元分析软件(ANSYS)对其周围流态进行仿真模拟,揭示不同倾斜角变化对人工鱼礁流场效应的影响,以期为四角锥台形人工鱼礁的设计提供参考依据。
1 材料与方法
1.1 计算流体动力学模型
该模拟计算的流体范围为长30 m、宽16 m、高16 m 的长方体区域,来流方向水平从左至右(图1)。计算所用鱼礁模型为正四角锥台形人工鱼礁,底面正方形边长为3 m,高度为3 m,在等底等高的情况下,通过改变顶面正方形边长以改变斜面倾角,由此得到5 个鱼礁模型(表1)。表1 中倾斜角在文章中指的是礁体侧面与底面所成的夹角,即斜面倾角,边长比(α)为正四角锥台形鱼礁上表面正方形边长(D)与下表面正方形边长之比(L),即α=D/L。等距改变顶面边长得到5 个边长比为0.2、0.4、0.6、0.8、1,对应5 种情况的倾斜角分别为68.2°、73.3°、78.7°、84.3°、90°。由于本研究只考虑倾斜角作为单一变化因素,考虑到开孔状态对流场的干扰,故模型做无孔设计。图2 和图3 分别为倾斜角73.3°(即上底边1.2 m,上下正方形边长比为0.4)的人工鱼礁的正视图与俯视图。鱼礁底部所置地面设为Z=0 m 的X-Y 平面,坐标原点在鱼礁底部中心点处。鱼礁迎流面底边离计算域入口8.5 m(礁体高度的2.8 倍),鱼礁背流面底边离计算域出口18.5 m(礁体高度的6.2 倍),礁体上表面离计算域顶部13 m(礁体高度的4.3 倍),礁体中心点到计算域两侧的距离为8 m(礁体高度的2.6 倍)。

图1 流体计算域Fig.1 Fluid computational domain

图2 礁体俯视图Fig.2 Vertical view of artificial reef

图3 鱼礁正视图Fig.3 Front view of artificial reef

表1 四角锥台形人工鱼礁的结构参数表Tab.1 Structure parameters of artificial reef
1.2 控制方程
该研究为探究鱼礁周围的流场效应的时间平均流特性,假定模型中流体为粘性不可压缩流体。水流控制方程采用定常、不可压缩流动下的连续性方程和Navier-Stokes 方程(N-S 方程)[27]:
连续方程:

动量方程:
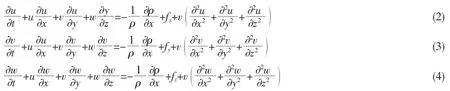
式中:u、v、w 分别为x、y、z 方向上的速度分量,m·s-1;v 为流体的运动学黏性系数,m2·s-1;t 为时间,s;ρ 为流体密度,kg·m-3;p 为压强,Pa;fx、fy、fz分别为x、y、z 方向上的单位质量力,m·s-2。
1.3 计算区域的网格划分
在计算区域的网格划分上,应用计算软件的自适应网格划分方式,划分成四面体非结构化网格。礁体附近区域最大层数设为8,增长率设为1.2,使数值模拟时可捕捉礁体的几何细节;在其他区域网格最大尺寸设为0.6 m。
1.4 边界条件
边界条件的设置,进口条件均设置为速度进口。通常情况下,近岸海水流速为1 m·s-1以内,以杭州湾为例,潮流平均速度约为0.2 m·s-1,而在涨落潮时平均速度达0.8 m·s-1[28]。故设置4 种流速分别为0.2、0.4、0.6 以及0.8 m·s-1。出口条件设置为压力出口。计算域两侧面以及顶面设置为对称边界条件。所有固体均采用无滑移条件。
1.5 数值算法
计算在ANSYS fluent 平台上完成。压力速度耦合用SIMPLEC 算法,压力项处理则用standard 差分格式[35],各方程的空间离散均采用QUICK 格式[36],计算残差值取10-5,计算的最大迭代步数在多次计算过程中平均500 步以后转为平稳,所以取500 步。
2 结果与分析
上升流会把深水区大量的海水营养盐(磷酸盐、硝酸盐等)带到表层,为鱼类生长带来丰富的饵料,因此,上升流显著的海区经常会形成著名的渔场。此外,水流流经礁石时,在礁石后面会产生一个漩涡区,即背涡流,涡流速度动态稳定。许多研究表明,鱼类常常聚集在珊瑚礁周围,因为其背流区内的不同水层更容易相互混合,其营养盐以及溶解盐也会高于正常水域,可以为鱼类提供有利的生长环境[29-30],且背涡流的影响效应与背涡区内部流态的范围大小、漩涡强度及大小等因素相关。因此,上升流以及背涡流的整体规模、涡量强度、速度方向等参数是衡量人工鱼礁效益的重要指标。
2.1 不同速度下的上升流与背涡流
文章以表1 中模型c(边长比0.6,倾斜角78.7°)为计算模型,对不同速度下的礁体周围流态进行了数值模拟。图4、图5、图6 分别为不同流速(0.2、0.4、0.6、0.8 m·s-1)下礁体周围水流在y=0 m 平面(侧面图)的速度矢量分布、涡量分布以及z=0.5 m 平面(俯视图)的速度矢量分布。为对各个速度下的情况进行合理比较,将各种情况下的比色棒所代表的速度统一大小区间。由于4 种来流速度是逐渐增大的,因此图4 和图6 中的4 幅图在主色调上有明显差异。
从速度矢量分布来看,不同来流速度,相同倾斜角的情况下,鱼礁周围流场的变化趋势相近,具体表现为流体变化的速度方向和影响范围相似,但是流速大小有明显差异(图4、图6)。另外,4 种速度下,涡量最大处均出现于鱼礁迎流面与上表面交汇处,还可以清晰地看出涡量较大处的规模随来流速度的增大同步增长,且其分布于后方延长处(图5)。

图4 4 种不同来流速度下y=0 平面上的速度矢量分布图(α=0.6)Fig.4 Velocity vector distribution on the plane y=0 at 4 different inflow velocities (α=0.6)
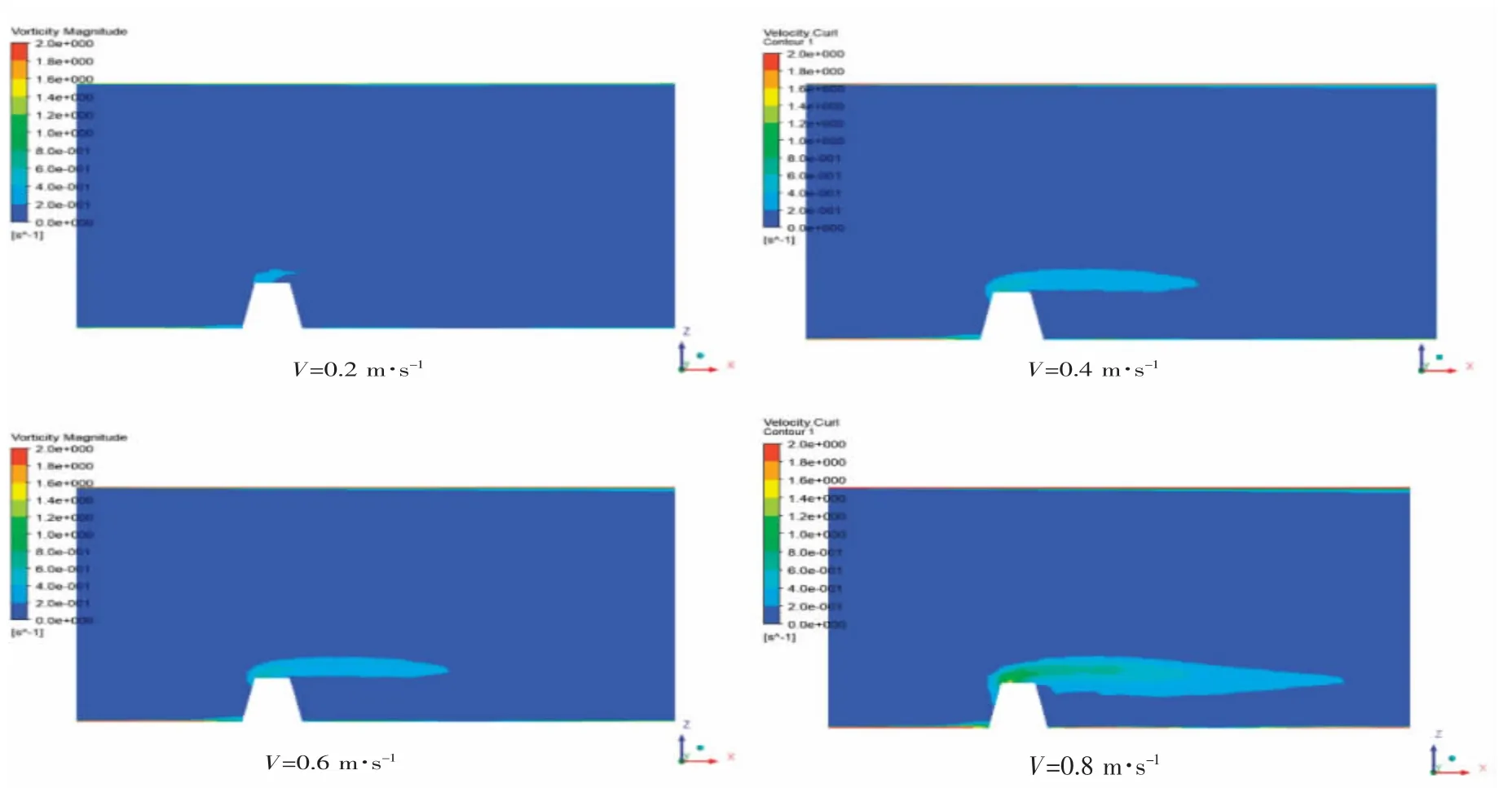
图5 4 种不同来流速度下y=0 平面上的涡量分布云图(α=0.6)Fig.5 Vorticity distribution cloud maps on the y=0 plane at four different inflow velocities (α=0.6)

图6 4 种不同来流速度下z=0.5 m 平面上的速度矢量分布图(α=0.6)Fig.6 Velocity vector distribution on the plane z=0.5 m at 4 different inflow velocities (α=0.6)
2.2 不同倾斜角下的上升流、背涡流、侧向流
根据礁体倾斜角的不同,迎流面的上后方会形成规模大小不等的上升流,由图7 可知,倾斜角大的鱼礁绕流的影响高度以及宽度都大于倾斜角小的绕流,且上升流规模大小随着倾斜角的增大而增大,这是由于随着迎流面积的增大,阻水能力增强所导致的。
从侧视角度(y=0 m 平面)来看,鱼礁后方的背涡流是一个顺时针漩涡,且随着鱼礁倾斜角的增大,它的基本形态不变,规模略微增大,涡心则向上偏移,且水平高度始终低于鱼礁顶面高度(图7)。

图7 5 种不同倾斜角下y=0 m 平面上的速度矢量分布图(v=0.4 m·s-1)Fig.7 Velocity vector distribution on the plane y=0 m at 5 different inclination angles (v=0.4 m·s-1)
鱼礁周围水体不仅会形成上升流,还会形成侧向流,且该平面内的速度最大处也出现在侧向流内,侧向流规模随着倾斜角的增大而增大,如图8 所示。在礁体迎流面两侧后方均会形成2 个方向相反的漩涡,这两个漩涡会形成1 个大漩涡区(即背涡区),且在相同来流速度下,倾斜角越大,其背涡区内的两个相反漩涡均更明显。背涡区的宽度以及长度均随倾斜角的增大而增大,且增幅较大。另外,当倾斜角越大,其后方的流态更为杂乱,这可能是由于倾斜角大的鱼礁在z=0.5 m 平面上方的体积更大,导致其对与z=0.5 m平面鱼礁后方的流态影响更为明显。

图8 5 种不同倾斜角下z=0.5 m 平面上的速度矢量分布图(v=0.4 m·s-1)Fig.8 Velocity vector distribution in the plane z=0.5 m with 5 different inclination angles(v=0.4 m·s-1)
图9 为5 种不同倾斜角下y=0 m 的平面上的涡量分布云图,该图显示不同倾斜角的鱼礁涡量最大值均出现在迎流面与鱼礁上表面相交处,但涡量范围差异并不明显,且除迎流面上方与上表面相交处的一小段弧形外,其余区域的涡量几乎为0。

图9 5 种不同倾斜角下y=0 m 平面上的涡量分布云图(v=0.6 m·s-1)Fig.9 Vorticity distribution cloud maps on y=0 m plane under 5 different inclination angles (v=0.6 m·s-1)
3 讨论与分析
3.1 相同倾斜角下的产生的展向涡和流向涡与背涡流的联系
当来流受到无孔礁体斜面的阻挡,流场有一个主要的流向时,流经礁体上表面的水体在其上方形成三角状涡旋区,产生了一个横向的涡,该涡旋与SWEARINGEN,et al[37]提到的对流向涡的概念相符合。而发现因无孔礁体斜面阻挡,来流在礁体斜面形成一对附着在其上的涡旋区,涡的方向和此流向垂直的涡旋也与WILLIAMSON[34]提到的展向涡描述相符。在稳定流中,由于鱼礁的不同面间构成交线(如迎流面与顶面)导致流体分离。随着流体连续流动,不断有动态稳定漩涡产生在分离点下游的壁面上,且不断从壁面上脱落,形成尾迹流。而脱落的漩涡将随流体对流发生粘性扩散,正是因为粘性扩散作用,漩涡的涡流强度在运动过程中不断减弱,直至消亡。从礁体壁面脱落的漩涡带有大量能量,该能量的产生与消耗具体表现是在礁体上施加一个阻力。同一倾斜角的鱼礁,在不同来流速度作用下,其周围所产生的流速大小、涡量大小有明显差异,将展向涡和流向涡与背涡流流场进行对比观察后发现,展向涡宽度与背涡流流场宽度近似相等,流向涡高度大于展向涡高度,流向涡涡心位置处的涡流高度与背涡流的高度近似相等,展向涡和流向涡长度近似相等,并且与背涡流的长度近似相等,与李晓磊等[31]的研究描述高度相似。而速度方向及影响规模等变化的差异不大,这与黄远东等[20]的研究结果一致。
3.2 倾斜角对上升流影响
OGAWA[2]、黄远东等[17]、何文荣等[22]和姜少杰等[32]将水流Z 方向速度分量与来流速度之比大于5%的水域作为上升流区域,本研究中亦据此选取上升流数据。
通过分析y=0 m 平面内的Z 方向的速度分量分布,求得上升流参数Hm/H(最大高度Hm 与礁体高度H 之比),得到上升流作用高度与礁体倾斜角之间的关系。图10 为在4 种不同来流速度下,各礁体所形成的最大上升流高度与礁体高度之比的折线图。根据前人的研究,得到梯形人工鱼礁Hm/H 值为2.49,箱形人工鱼礁Hm/H 值为2.63,姜少杰等通过对正六棱柱式人工鱼礁的模拟计算得到Hm/H为2.85,而文章中正四角锥台形鱼礁Hm/H 范围在2.25~2.8 之间,与前人的结论相近。当来流速度相同时,随着倾斜角的增加,曲线a(倾斜角68.2°)变化到曲线b(倾斜角73.3°)的过程中,上升流作用最大高度(Hm)与礁体高度(H)之比Hm/H 增速较大,而在曲线d(倾斜角84.3°)之后,虽然Hm/H 依然在增加,但是增速明显放缓。a、b 两种情况在低速条件下(0.2~0.4 m·s-1),其速度增加使Hm/H 有一定的提高,但大多数情况下,随着速度的增大,上升流最大高度与鱼礁高度之比Hm/H 几乎不变化,即来流速度的变化与上升流最大高度无明显的相互关系。
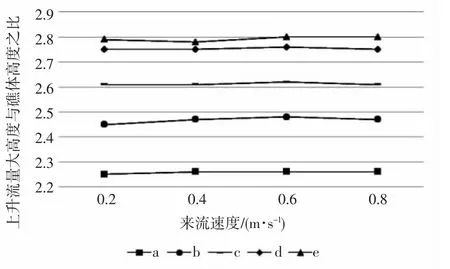
图10 不同倾斜角、不同来流速度下Hm/HFig.10 The ratio of maximum upwelling height to reef height under different inclination angles and different inflow velocities
3.3 倾斜角对背涡流影响
本研究中数值计算试验的背涡流模拟结果与TENEDA[30]采用流体显示技术,在低雷诺数时圆柱绕流产生的圆柱尾涡(双涡)的结果相吻合,TENEDA的试验结论目前仍是数值模拟工作者验证算法准确性的标准之一。漩涡的流速分布为由外向内逐渐减小,涡心处流速趋近于零,该结论与李晓磊等[31]的研究结果一致。
对背涡流的最大涡量值进行分析,如图11 所示,随着来流速度的增大,最大涡量值也会随之增大,且其呈线性关系。而来流流速相同的情况下,随着倾斜角的增大,最大涡量值呈现出一种先增后减的趋势,且当倾斜角为78.7°时,相较于其余4 种情况,最大涡量值达到峰值。通过与何文荣等[22]的金字塔型鱼礁后方背涡流情况进行比较发现,文章中5 种倾斜角的鱼礁的背流区高度均高于金字塔型鱼礁的背流区,这是由于本研究中的鱼礁的背流面面积均大于金字塔型鱼礁,且迎流面与地面的夹角同样大于金字塔型鱼礁。
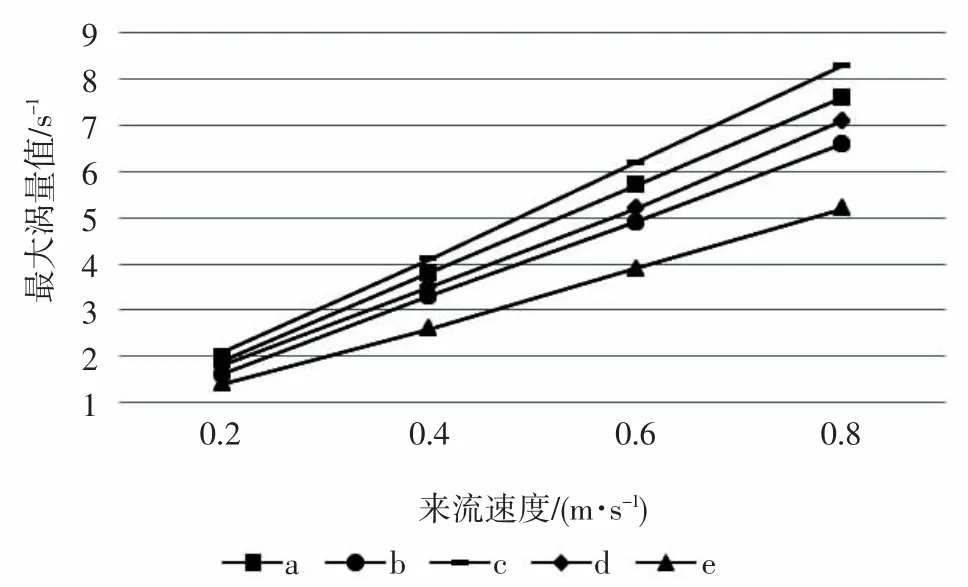
图11 不同倾斜角、不同来流速度下在y=0 平面的最大涡量值(s-1)Fig.11 The maximum vorticity value in the y=0 plane under different inclination angles and different inflow velocities (s-1)
4 结论
文章基于ANSYS 有限元分析软件,对不同倾斜角的四角锥台形人工鱼礁在水流中的三维流场效应进行了数值仿真。文中对不同流速情况下同一倾斜角鱼礁礁体周围流态情况进行了分析,并在同一流速下改变礁体倾斜角,就上升流和背涡流的水动力学特性进行比较。由此得出以下结论:
(1)在不同来流速度下,同种倾斜角鱼礁周围流场流速大小、涡量大小有明显差异,但是流体变化趋势即速度方向和影响范围相似。
(2)通过分析y=0 m 平面以及z=0.5 m 平面上流体的速度分布,揭示倾斜角对人工鱼礁的流场效应具有显著影响:1)礁体迎流面与上表面交汇处形成流动分离点,在礁体上表面形成小漩涡区,在礁体后方形成尾涡区。2)最大上升流高度与礁体高度之比以及上升流的规模大小均随倾斜角的增大而增大,其值与来流速度大小无明显关联。3)鱼礁的倾斜角越大,其背流区规模越大。4)随着倾斜角的增大,鱼礁背部的尾涡基本形态不变,规模略微增大,涡心向上偏移,且水平高度始终低于鱼礁顶面高度。5)倾斜角越大,鱼礁后方流态越杂。
(3)通过分析y=0 平面上流体的涡量分布,得出:1)鱼礁迎流面上方与上表面相交处为涡量值最大处,其他区域的涡量几乎为0。2)来流速度相同的情况下,随倾斜角的增大,最大涡量值呈现一种先增大后减小的趋势,相较于另外4 种情况,当倾斜角为模型c 情况下(78.7°),最大涡量值达到峰值。
本研究尚存在一定不足之处,首先是未能开展模型试验与数值模拟结果进行对比验证。此外,为单纯研究倾斜角的影响,鱼礁被设计为无孔模型,避免开孔后流体干扰,但是,实际应用中的鱼礁势必为有孔设计。以上问题在后续的研究工作中将进一步修正和完善,为人工鱼礁的优化设计提供更全面的参考依据。
