Degenerate s-Extended Complete and Incomplete Lah-Bell Polynomials

Hye Kyung Kimand Dae Sik Lee

1Department of Mathematics Education,Daegu Catholic University,Gyeongsan,38430,Korea

2School of Electronic and Electric Engineering,Daegu University,Gyeongsan,38453,Korea

ABSTRACT Degenerate versions of special polynomials and numbers applied to social problems,physics,and applied mathematics have been studied variously in recent years.Moreover,the(s-)Lah numbers have many other interesting applications in analysis and combinatorics.In this paper,we divide two parts.We first introduce new types of both degenerate incomplete and complete s-Bell polynomials respectively and investigate some properties of them respectively.Second,we introduce the degenerate versions of complete and incomplete Lah-Bell polynomials as multivariate forms for a new type of degenerate s-extended Lah-Bell polynomials and numbers respectively.We investigate relations between these polynomials and degenerate incomplete and complete s-Bell polynomials,and derive explicit formulas for these polynomials.

KEYWORDS Lah-Bell numbers and polynomials; s-extended Lah-Bell numbers and polynomials;complete s-Bell polynomials;incomplete s-Bell polynomials; s-Stirling numbers of second kind

1 Introduction

For nonnegative integersn,k,ssuch thatn≥k,thes-Lah numberLs(n,k)counts the number of partitions of a set withn+selements intok+sordered blocks such thatsdistinguished elements have to be in distinct ordered blocks [1–5].Whens=0,the Lah numbers appears non-crossing partitions,Dyck paths as well as falling and rising factorials [6].As multivariate forms for ordinary Bell polynomials and Stirling numbers of the second kind,respectively,both the complete and incomplete Bell polynomials play important role in combinatorics and number theory.Recently,many mathematicians have been studying various degenerate versions of special polynomials and numbers as well as enumerative combinatorics,probability theory,number theory,etc.[7–17].In [7],as an example considering the psychological burden of baseball hitters,it well expresses the starting point of degenerate special polynomials and numbers being studied by many scholars.Also,both the complete and incomplete Bell polynomials are multivariate forms for Bell polynomials and Stirling numbers of the second kind,respectively.Beginning with Bell [18],these polynomials have been studied by many mathematicians [1,16,19,20].Recently,Kwon et al.[16] introduced the degenerate incomplete and completes-Bell polynomials and Kim et al.[20] introduced the incomplete and completes-extended Lah-Bell polynomials,respectively.With this in mind,we want to study the degenerate versions of complete and incomplete Lah-Bell polynomials as multivariate forms for a new type of degenerates-extended Lah-Bell polynomials and numbers respectively.In Section 2,we consider new types of degenerate incomplete and completes-Bell polynomials respectively different from those introduced in [16] for our goal.We study several properties and explicit formulas for them.In Section 3,we define both degenerate incomplete and completes-extended Lah-Bell polynomials associated with a new type of degenerates-extended Lah-Bell polynomials respectively,and derive relations between these polynomials and degenerate polynomials in the first part.We also investigate explicit formulas for degenerate complete and incompletes-extended Lah-Bell polynomials,respectively.

First,we introduce some definitions and properties we needed in this paper.

For a nonnegative integers,thes-Stirling numbersS(s)2(n,k)of the second kind are given by the generating function

Whens=0,,k)=S2(n,k)are the Stirling numbers of the second kind which are the number of ways to partition a set withnelements intoknon-empty subsets.

From (8),it is to see that [15,16] the generating function of thes-Bell polynomials is

Furthermore,the incompletes-Bell polynomials.

Bn+s,k+s(β1,β2,···:ν1,ν2,···)are given by the generating function

Whens=0,Bn+0,k+0(β1,β2,···:ν1,ν2,···)=Bn,k(β1,β2,···,βn－k+1)are the incomplete Bell polynomials.From (10),we obtain immediately that [16]

whereΛ(n,k,s)denotes the set of all nonnegative integers(ki)i≥1and(si)i≥0such that

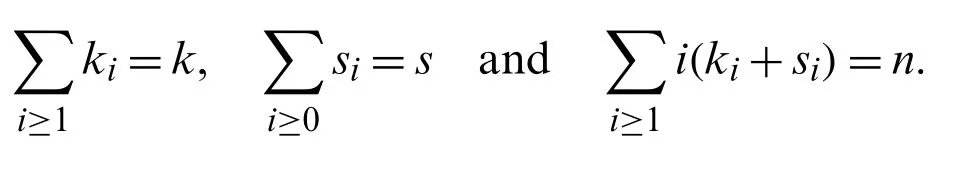
The combinatorial meaning of the incompletes-Bell polynomials is in the reference [18].

The completes-Bell polynomialsB(s)n (x1,x2,··· :y1,y2,···)are given by the generation function

whereexp(t)=et.

Whens=0,B(0)n (β1,β2,···:ν1,ν2,···)=Bn(β1,β2,···,βn)are the complete Bell polynomials.

Letn,k,sbe nonnegative integers withn≥k.It is well known that [2] an explicit formula and the generating function ofs-Lah BellLs(n,k)are given by,respectively

and

Whens=0,L0(n,k)=L(n,k)are the unsigned Lah-numbers.

Kim et al.[2] introduced thes-extended Lah-Bell polynomialsLbn,s(x)given by the generating function

Whenx=1,are called thes-extended Lah-Bell numbers.Whens=0,Lbn,0(x)=Lbn(x)are the Lah-Bell polynomials.

Forλ∈R,the degenerate exponential function is defined by

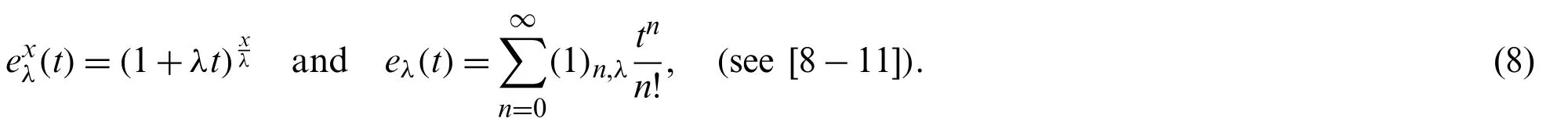
where(x)0,λ=1 and(x)n,λ=x(x－λ)(x－2λ)···(x－(n－1)λ).

The degenerate fully Bell polynomials are given by

Whenλ→0,Beln,λ(x)=beln(x).

In addition,the partially degenerate Bell polynomials are given by

Whenλ→0,Beln,λ(x)=beln(x).

2 A New Type of Degenerate Complete and Incomplete s-Bell Polynomials

In this section,we introduce new types of degenerate completes-Bell polynomials and degenerate incompletes-Bell polynomials different from (9) and (10),respectively.We also give some identities and explicit formulas for these polynomials.

For our goal,we introduce a new type of the degenerate extendeds-Bell polynomials defined by

Whenx=1,beln,s,λ=beln,s,λ(1)are called the degenerate extendeds-Bell numbers.

When limλ→0eλ(x(et－1))esλ(t)=exp(x(et－1))exp(t)=

Whens=0,beln,0,λ(x)=beln,λ(x)are the degenerate Bell polynomials.

Theorem 2.1.Forn,s∈N ∪0,we have

Proof.From (1),(8) and (11),we observe that

By comparing with the coefficients of both side of (12),we get the desired result.

Theorem 2.2.Forn,s∈N ∪0,we have

Proof.From (8) and (11),we observe that

By comparing with the coefficients of both side of (13),we get the desired result.

First,we define a new type of the degenerate complete Bell polynomialsBλn(β1,β2,···,βn)associated with the degenerate Bell polynomialsbeln,λ(x)by

and a new type of the degenerate incomplete Bell polynomials1,β2,···,βn－k+1)associated with some degenerate Stirling numbers defined by

Theorem 2.3.Forn≥k≥0,we have

In particular,we haveWλn(x,x,···,x)=beln,λ(x).

Proof.From (3),(4) and (14),we have

Therefore,by comparing with coefficients of both sides of (16),we have the desired result.

In particular,from (16),we have

Thus,by comparing with coefficients of both sides of (17),we have

Wλn(x,x,...,x)=beln,λ(x).

In next theorem,we obtain a new type of degenerate Stirling numbers of second kind(1)k,λS2(n,k).

Theorem 2.4.Forn≥k≥0,we have

In particular,we get1,1,...,1)=(1)k,λS2(n,k).

Proof.From (8),(14) and (15),we observe that

Therefore,by comparing with coefficients of both sides of (18),we have what we want.

In addition,from (18),we get

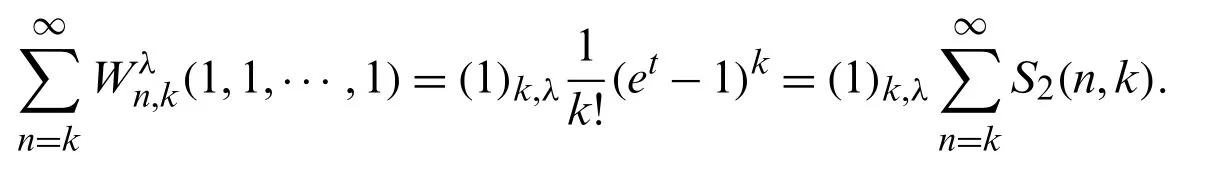
Thus,we have1,1,···,1)=(1)k,λS2(n,k).

Next,forλ∈R,we consider a new type of degenerate incompletes-Bell polynomials defined by

From (4) and (19),we have the following explicit formula

Forn≥k≥0,we have

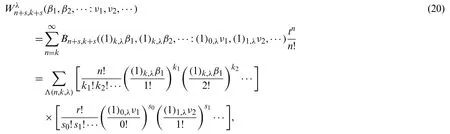
whereΛ(n,k,s)denote the set of all nonnegative integers(ki)i≥1and(si)i≥1such that

Naturally,we define a new type of the degenerate completes-Bell polynomials by

whereλ∈R andn,k∈N withn≥k.

We note that

From (19) and (21),we note that

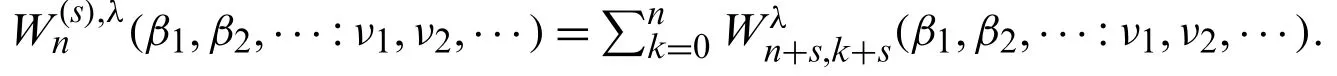
Theorem 2.5.Forn,k,s≥0 withn≥k,we have

Proof.From (1),(8) and (19),we have

Therefore,by comparing with coefficients of both side of (22),we obtain the desired result.

In Theorem 2.5,we obtain a new type of degenerates-extended Stirling number of second.

Theorem 2.6.Forn≥k≥0,we have

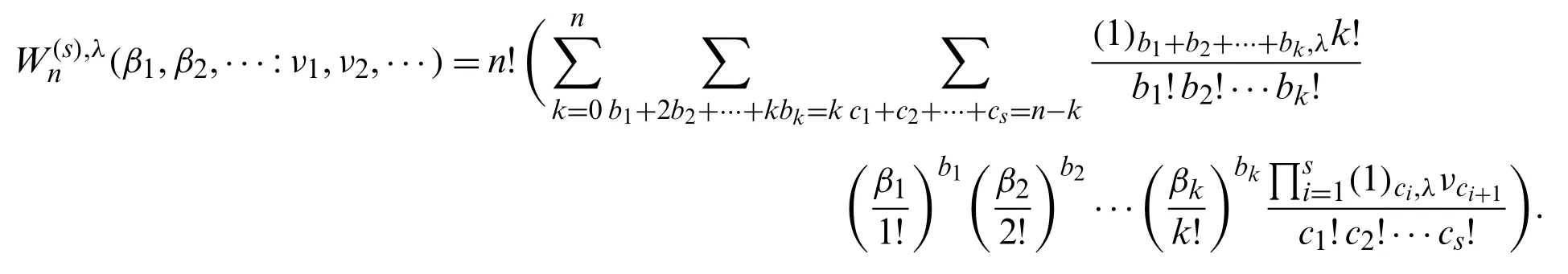
Proof.By using (8),we observe that

From (23) and (24),we get

On the other hand,from (21),we have

Thus,by comparing with coefficients of (25) and (26),we have what we want.

Next,we consider the extended degenerate completes-Bell polynomials defined by the generating function

Theorem 2.7.Forn≥k≥0,we have

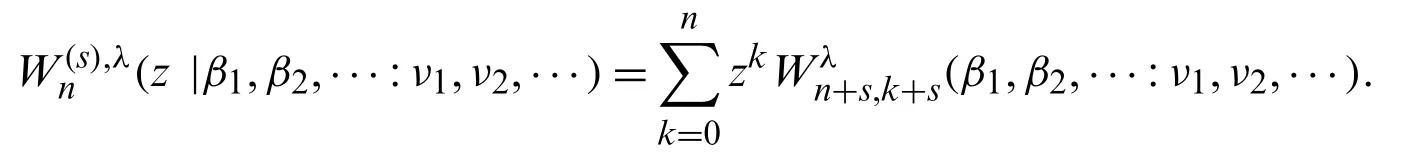
Whenz=1,we get

Proof.From (19) and (27),we have

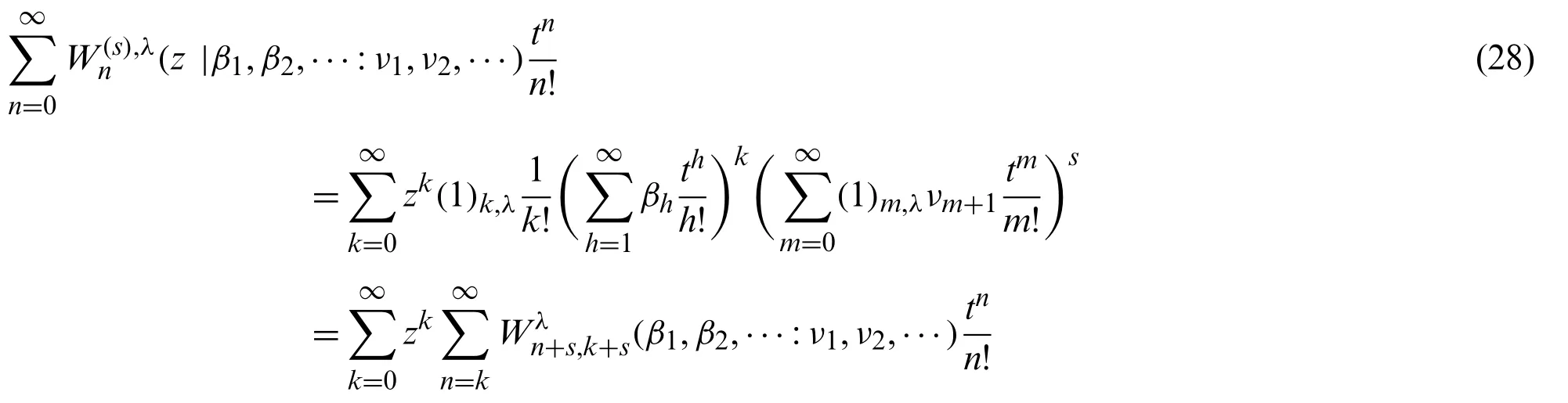
Thus,by comparing with coefficients of both sides of (28),we have what we want.

Theorem 2.8.Forn,k,s≥0 withn≥k,we have

Proof.From (27),we observe that

On the other hand,from (11),we get

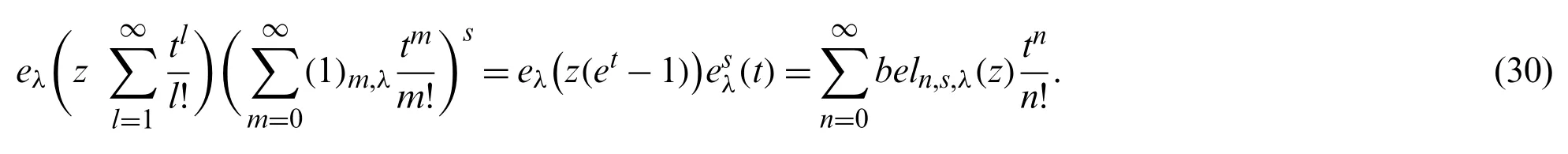
Thus,from (29) and (30),we get the desired result.

3 Degenerate s-Extended Complete and Incomplete Lah-Bell Polynomials

In this section,we introduce a new type of the degenerate Lah-Bell polynomials different from Kim-Kim’s in [8] and define both thes-extended complete and incomplete degenerate Lah-Bell polynomials associated with a new type of the degenerate Lah-Bell polynomials.We also demonstrate some interesting properties related to these polynomials and explicit formulas for them.

We consider a new type of the degenerate Lah-Bell polynomialsLbn,λ(x)given by the generating function

Whenx=1,Lbn,λ(1)=Lbn,λ (n≥0)are called the degenerate Lah-Bell numbers (see Figs.1 and 2).

Whenλ→0,Lbn,λ(x)=Lbn(x).

In view of the ordinary Bell polynomials,the degenerate 2s-extended Lah-Bell polynomials are defined by the generating function

Whenx=1,Lbn,2s,λ=Lbn,2s,λ(1)are called the degenerate extended 2s-extended Lah-Bell numbers numbers.Whens=0,the degenerate completes-extended Lah-Bell polynomials are the degenerate Lah-Bell polynomials.

Next,we introduce the degenerate complete Lah-Bell polynomialsLWλn(x1,x2,···,xn)defined by the generating function

We note that

From (31),we haveLWλn(x,···,x)=Lbn,λ(x)andLWλn(1,1,···,1)=Lbn,λ.

From (20) and (34),we get

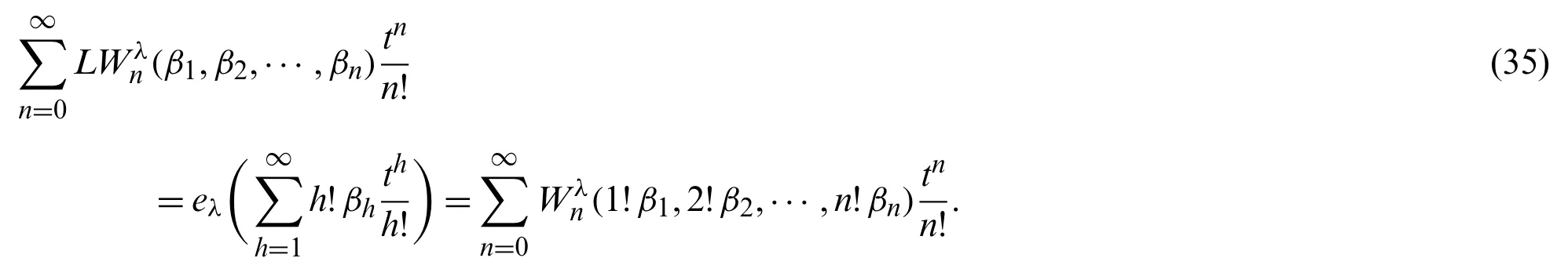
By (14),(15),(35) and Theorem 2.3,we obtain the following theorem.

Theorem 3.1.Forn≥k≥0,we have

Naturally,we can define a new type of the degenerate incomplete Lah-Bell polynomials

1,β2,···,βn－k+1)are defined by the generating function

Note that whenλ→0,1,1,···,1)=Lbnare the Lah-bell numbers.

From (15) and (36),we observe that

Theorem 3.2.Forn≥k≥0,we have

Proof.

From (8),(36) and (37),we observe that

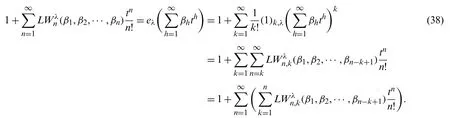
Therefore,by comparing with coefficients of both side of (38),we get the desired identity.

We define the degenerates-extended incomplete Lah-Bell polynomials

1,β2,···:ν1,ν2,···)by the generating function

Whens=0,the degenerate incompletes-extended Lah-Bell polynomials are the degenerate incomplete Lah-Bell polynomials.

From (19) and Theorem 2.5,we get easily the following explicit formula.

Theorem 3.3.Forn≥k≥0,we have

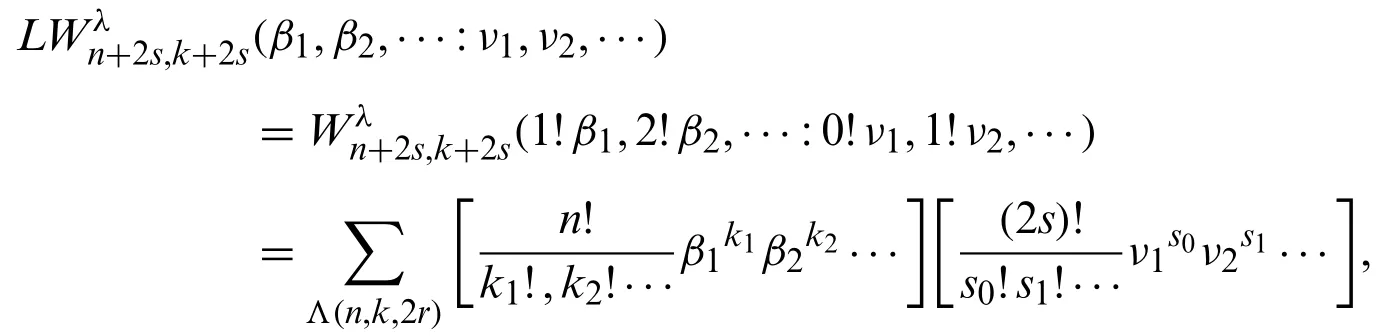
whereΛ(n,k,2s)denote the set of all nonnegative integers {ki}i≥1and {si}i≥0such that

We also define the degenerates-extended complete Lah-Bell polynomials

|β1,β2,···:ν1,ν2,···)by the generating function

Theorem 3.4.Forn≥k≥0,we have

Whenx=1,we have

Proof.From (32) and (39),we have

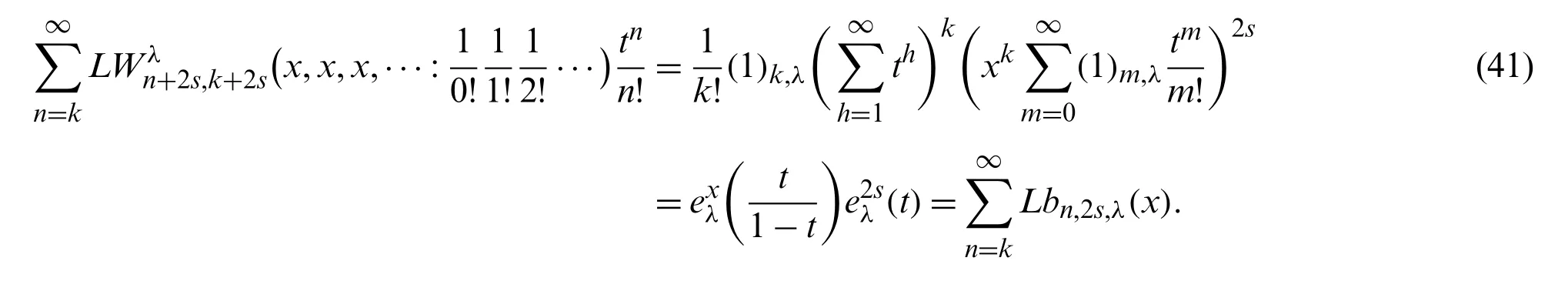
Therefore,by comparing with coefficients of both side of (41),we get the desired result.

From (19),(39) and (40),we note that

forn≥k≥0.

Theorem 3.5.Forn≥k≥0 ands≥0,we have

Proof.From (17),we have

and

By (42) and (43),we have

Therefore,by comparing with coefficients of both side of (44),we get the desired result.

Remark.We recall the degenerate Lah-Bell numbersLbn,λas follows (31):

In the following figures (x-axis=t,y-axis=in which the simulation program uses Fortran language,We can see the changeLbn,λdepending onλ.

Figure 1:Degenerate Lah-Bell numbers when λ=0.1 and λ=0.5,respectively

Figure 2:Degenerate Lah-Bell numbers when λ=1.0 and λ=2.0,respectively

4 Conclusion

In this paper,we introduced both the degenerates-extended incomplete and complete Lah-Bell polynomials associated with a new type of degenerates-extended Lah-Bell polynomials.We demonstrated some combinatorial identities between these polynomials and polynomials introduced in Section 2,and explicit formulas for them respectively.In addition,we obtained new types of the degenerate Stirling numbers ands-extended Stirling numbers of the second kind in Theorem 2.4 and 2.5,respectively.

Special polynomials have been applied not only in mathematics and physics,but also in various fields of application [1,3,6,9,17,18,22–27].In recent years,one of our research areas has been to explore some special numbers and polynomials and their degenerate versions,and to discover their arithmetical and combinatorial properties and some of their applications.We intend to study various degenerate polynomial and numbers using several means such as function generation,combinatorial methods,umbral calculus,differential equations,and probability theory.

Acknowledgement: The authors would like to thank the referees for the detailed and valuable comments that helped improve the original manuscript in its present form.Also,the authors thank Jangjeon Institute for Mathematical Science for the support of this research.

Ethics Approval and Consent to Participate: The authors declare that there is no ethical problem in the production of this paper.

Consent for Publication: The authors want to publish this paper in this journal.

Funding Statement: This work was supported by the Basic Science Research Program,the National Research Foundation of Korea (NRF-2021R1F1A1050151).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.