基于zonotope的离散时间Markov跳变系统的状态区间估计

荆苗苗，李晓航

(上海工程技术大学 电子电气工程学院,上海 201600)

0 引 言

在大多数控制策略中，例如滑模控制[1-2]，自适应控制[3]和其他一些控制方法[4]，准确地估计系统状态非常重要。然而，对于大多数系统来说，状态的测量是困难的。因此，具有未知输入系统的观测器设计(通常称为未知输入观测器(UIO))是现代控制理论中讨论最重要和最有意义的问题之一。此外，基于混沌的安全通信设计中的外部干扰，执行器故障或保密通信中的有效信息都可以视为系统的未知输入。因此，未知输入观测器在许多领域都有着重要的应用价值，包括容错控制设计，故障诊断和隔离以及基于混沌同步的安全通信等[5-8]。自从20世纪70年代未知输入观测器被提出以来，已经受到了学者们广泛的关注，并提出了很多设计方法[9-12]。例如，文献[9]在观测器匹配条件不满足的前提下，基于构造辅助输出的方法，提出一种状态和未知输入同时估计的未知输入观测器设计方法。文献[10]针对过程和测量中均出现未知输入的线性连续系统，提出了一种全阶PI观测器，不仅可以估计出系统状态，还可以估计未知的输入。文献[11]考虑具有未知输入不匹配的线性系统，通过引入未知输入建模来解耦不匹配的未知输入。

马尔科夫跳变系统(Markov jump systems，MJS)是由几个子系统或模态组成，这些子系统或模态可以从一种模态随机切换到另一种模态。在实际应用中，马尔科夫跳变系统可以用来描述由系统受到外界干扰、元件故障或维修、突发环境因素干扰导致的随机突变的情况。目前，马尔科夫跳变系统在制造业控制系统、容错系统、航空航天等领域得到了广泛的应用，并且在稳定性分析[13]，控制器设计[14-15]，故障诊断和容错控制[16]等方面取得了大量的研究成果。

集员估计可以有效地处理未知但有界的不确定性带来的影响[17]。常用的几何体有区间、椭球、平行多面体和中心对称多胞体(zonotope)，其中基于中心对称多胞体的方法因其计算量小，保守性低，从而吸引了很多学者的关注[18-21]。文献[17]研究了集员估计在故障诊断和容错控制上的应用；文献[18]提出了一种将未知输入观测器与集员方法相结合进行鲁棒故障诊断的方法，通过解耦部分未知输入对状态估计大小的影响，从而降低鲁棒状态估计的保守性。此外，文献[19]提出了一种基于zonotope的动态系统集成员方法，其中在求解凸优化问题时，每个样本区域的体积都达到最小。实际上，系统由于建模的不确定性、未知扰动以及测量噪声的存在，会降低故障诊断的准确性，从而造成一些无法估量的结果，而集员估计可以通过假设干扰和噪声有界，利用几何体近似可行集来有效地处理由鲁棒估计产生的误差，因此，本文考虑使用集员估计方法来估计误差的区间，从而提供可靠的估计信息。

本文研究了离散马尔科夫跳变系统在仅知道部分转移概率边界的情况下的状态区间估计问题。首先，提出了一种新的状态转移概率，其中每个转移概率值是未知的，或者边界是已知的。在此基础上，提出了一种降维未知输入观测器的设计方法，分析系统的鲁棒稳定性能并给出观测器存在的充分条件。与已有的Markov跳变系统分析方法相比，本文所提出的方法更具有一般性和实用性。然后通过中心对称多胞体计算出状态的区间估计，所求得的系统的状态值更加准确。最后，通过数学仿真，验证了该方法的有效性。

符号说明：对于矩阵A，AT和A⊥代表矩阵A的转置矩阵和正交补，A>0(A<0)表示矩阵A为正定(负定)矩阵，He(A)用来表示He(A)=A+AT。文中的星号*表示对称矩阵中相应位置的转置。

1 系统模型

考虑具有未知输入的线性离散时间马尔科夫跳变系统，即

(1)

(1)式中：xk∈Rn；uk∈Rm；yk∈Rp分别为状态，输入和输出向量。dk∈Rq为未知输入。矩阵A(rt)∈Rn×n,B(rt)∈Rn×m,D(rt)∈Rn×q和C(rt)∈Rp×n为适当维数的矩阵。{rk,k≥0}是在有限集R={1,2,…,N}内的离散时间状态的马尔科夫过程，具有如下状态转移概率，即

Pr(rk+1=j|rk=i)=πij

(2)

在本文中，假设系统的一部分转移概率是可量测的，因此，转移概率矩阵∏的形式为

(3)

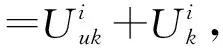
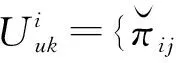
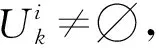
定义1一个m维中心对称多胞体Z⊂Rn是超立方体Bm=[-1,1]m在R中的映射,即

Z=p⊕HBm={p+Hz:z∈Bm}

(4)

(4)式中：⊕表示闵可夫斯基和，常向量p∈Rn称为Z的中心，H∈Rn×m称为Z的生成矩阵，为了简化，本文用〈p,H〉来描述中心对称多胞体Z。

性质1在中心对称多胞体的运算中，有如下性质：

〈p1,H1〉⊕〈p2,H2〉=〈p1+p2,[H1H2]〉

Le〈p,H〉=〈Lp,LH〉.

性质2对于中心对称多胞体Z，包围它的最小间隔向量可以由Box(S)=[a,b]表示，其计算方式为

(5)

(5)式中：Hij是第i行第j列的元素。

为降低中心对称多胞体的维数，本文采用文献[22]中提到的一种约化算子方法，将中心对称多胞体的阶数降低到一个范围内。定义降阶后的中心对称多胞体为Res(H)，(6)式成立。

Z=〈p,H〉⊆〈p,Res(H)〉

(6)

(6)式中：Res(H)∈Rn×l是由文献[22]提出的降阶方法获得的新生成的矩阵，n≤l≤m是中心对称多胞体的最大阶数。

假设1不失一般性，假设系统(1)的状态变量初值，未知输入均为未知但有界，且满足

(7)

定义2[23]对于uk≡0，dk≡0，以及任意初始条件x0∈in和r0∈R，有

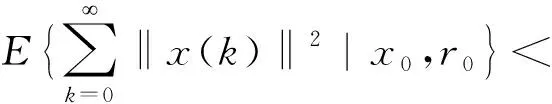
(8)

(8)式中：E表示数学期望，则系统(1)是随机稳定的。

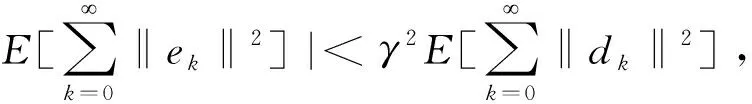
引理1(Finsler引理)[24]对向量x∈Rn，矩阵L∈Rn×n和U∈Rn×m，以下描述等价：

①xTLx<0，∀x≠0，U⊥x=0；

②U⊥L(U⊥)T<0；

③∃Y∈Rm×n使得L+UY+YTUT<0；

其中，U⊥为任意满足U⊥U=0的矩阵。

2 降维观测器设计

针对系统(1)，本节将提出一种离散时间Markov跳变系统的降维观测器设计方法，考虑系统(1)，当rk=i，系统模型表示为

(9)

(9)式中：A(rt)、B(rt)、C(rt)、D(rt)分别由Ai、Bi、Ci、Di表示。

分解系统向量xk=[x1(k)x2(k)]T,其中，x1(k)∈Rp。同时分解(3)中的系数矩阵

(10)

(11)

(10)—(11)式中：Ai,11∈Rp×p,Bi,1∈Rp×m,Di,1∈Rp×q。

不失一般性，假设Ci=[Ip0]，可以得到

θ1(k)=x1(k)=y(k)

(12)

θ2(k)=[KiIn-p]x(k)=Kix1(k)+x2(k)=

Kiy(k)+x2(k)

(13)

由(13)式可知

θ2(k+1)=[KiIn-p]xk+1=

(KiAi,12+Ai,22)θ2(k)+

[(KiAi,11+Ai,21)+Ki(Ai,22-KiAi,12)]y(k)+

(KiBi,1+Bi,2)u(k)+(KiDi,1+Di,2)d(k)

(14)

设计如下降维观测器系统：

(15)

(KiAi,12+Ai,22)ek+(KiDi,1+Di,2)dk

(16)

3 主要结论

考虑运用鲁棒方法对系统(1)进行H∞性能分析。有如下定理。

定理1如果对于给定标量γ>0，η和矩阵Gi∈R(n-p)×(n-p)，Wi∈R(n-p)×(n-p)，使得对于∀i∈S，下列线性矩阵不等式成立：

(17)

(18)

(17)—(18)式中：

KiAi,12)};

φ2=ηGi(Di,2+KiDi,1);

δ1=-Pi+I+He{ηGi(Ai,22+KiAi,12)};

δ2=ηGi(Di,2+KiDi,1);

(19)

将(16)代入(19)可得

E[ΔV(ek,rk)]≤

(20)

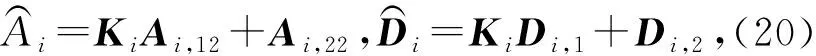
(21)

(21)式中：

在零初始条件下，针对系统(3)，考虑以下函数，并引入如下的H∞性能指标γ，定义函数

通过计算，进一步可得

(22)

(22)式中：

(23)

(24)

则

如果有Ωi,1<0和Ωi,2<0，可得

(25)

(26)

(25)—(26)式中：

根据引理1，(25)式和(26)式等价于存在矩阵Gi使得下式成立

(27)

(28)

定义

(29)

将(29)分别代入(27)和(28)式，可以得到

(30)

(31)

(30)—(31)式中：

φ2=ηGi(Di,2+KiDi,1)；

δ1=-Pi+I+He{ηGi(Ai,22+KiAi,12)}；

δ2=ηGi(Di,2+KiDi,1)；

注意GiKi=Wi.

(30)式、(31)式分别等价于(23)式、(24)式。由此，可以得到J≤V(e0,r0)，即在零初始条件下J≤0。定理1证明结束。

在得到状态的估计后，定理2通过zonotope理论给出误差e(k)的上下界，然后可以通过以下方式计算状态的准确间隔：

(32)

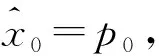
(33)

(33)式中：h=1,2,…,n,j=1,2,…,s，s是Hi(k)的列，Hi(k)满足如下递归方程

ex(0)∈〈0,H0〉

由性质1和误差系统(16)可以推导出

e(k+1)∈Λ(k+1)=

(KiAi,12+Ai,22)⊙〈0,Hi(k)〉⊕

(KiDi,1+Di,2)⊙〈0,Hd〉

从而有

e(k+1)∈Λ(k+1)=〈0,(KiAi,12+

Ai,22)Hi(k)〉⊕〈0,(KiDi,1+Di,2)Hd〉=

〈0,[(KiAi,12+Ai,22)Hi(k) (KiDi,1+Di,2)Hd]〉

以此类推，可以得到

Λ(k+1)=

即Λ(k+1)=〈0,Hi(k+1)〉, 其中，

根据定义1和性质2，可以得到误差e(k)的边界为

(h=1,2,…,n)

(34)

(34)式中：e(k)+，e(k)-代表e(k)的上界和下界。因此，状态的区间估计计算如下

(35)

定理2证明结束。

4 仿 真

为了证明本文所提方法的有效性，考虑如下具有2个模态的数值Markov跳变系统，相关参数为

根据定理1，可以求得

P1=15.105 8,P2=172.581 1,

K1=-2.141 3,K2=-1.598 5,

W1=-106.359 7,W2=-92.423 5。

图1 本文与文献[15]的结果对比Fig.1 Comparison of the results in [15] with this paper

图2 本文与文献[15]的结果对比Fig.2 Comparison of the results in [15] with this paper

P1=1.396 1,P2=10.361 0,

K1=-1.960 3,K2=-0.747 5,

W1=-7.134 3,W2=-3.056 7。

仿真结果如图3—图4所示。由图3—图4可知，本文所提出的方法可以很好地适用于部分已知转移概率的MJS，具有一般性和实用性。

图3 系统状态x1及其上下界的估计Fig.3 System state x1and estimation of its upper and lower bounds

图4 系统状态x2及其上下界的估计Fig.4 System state x2and estimation of its upper and lower bounds

5 总 结

本文针对存在未知输入的线性离散系统，设计了一种基于未知输入的降维观测器。首先通过李亚普诺夫函数使设计的降维观测器是可行的，基于中心对称多胞体理论表示系统状态的区间估计，并利用中心对称多胞体的性质来处理未知输入的不确定性。然后通过所设计的降维观测器估计出系统状态的上下边界。最后，通过一个数值仿真验证了所提方法的有效性。本文所提出的区间估计方法，由于中心对称多胞体的计算量小，保守性低，使得系统的状态估计更加准确。但是本文只研究了线性离散系统的区间估计方法，如何将本文所提出的方法推广到更具一般性的非线性系统中，是下一步要研究的方向。