基于动态稳定域的车辆横纵向稳定性协同控制*

丛森森，高 峰，许述财

（1.清华大学苏州汽车研究院（相城），苏州 215133；2.清华大学，汽车安全与节能国家重点实验室，北京 100084）

前言

随着感知技术和智能算法的发展，智能车辆（intelligent vehicle，IV）得到了迅速发展。通过完备的交通环境感知和精准的车辆控制算法，IV 可以有效地提升道路安全。从控制理论角度来看，车辆稳定控制的重点是运动学和动力学控制。车辆动态稳定性对车辆运动学控制有着重要影响，可进一步提升车辆安全性。因此，研制一套完善的车辆动态横纵向稳定性控制器具有重要意义。

在理想横摆角控制和电子稳定控制ESC等稳定控制理论中，基于稳定域的稳定性控制作为一种直观可靠的方法得到了广泛研究。通常车辆稳定域可以通过侧倾指数等稳定性指标或相平面区域阈值来定义。基于稳定域的控制通常在车辆失去稳定状态的临界时主动干预，可由接近稳定域边界的车辆状态表示。因此，基于稳定域的控制既可开发出独立的车辆控制方法，又可与其他控制目的相结合。

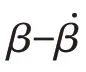
虽然基于稳定域的车辆稳定性控制方法已得到广泛应用，但其在稳定性控制方面仍有一些不足。首先，虽然稳定域边界被准确清晰的推演，但在实际应用过程中缺乏直观简便的描述。由于不同稳定域相对于不同车速和转向角度可显著移动，在面对不同转向角度和车速时因缺乏直观表达而难以实际应用。其次，虽然车辆稳定状态由稳定域外被控制回稳定域内，但只有在车辆状态离开稳定域后才触发控制策略。对于IV 而言，即使是轻微或暂时不稳定的车辆状态也会存在安全隐患。最后，在固定车辆动力学参数基础上，车辆稳定域近似不变，基于不同车况下的动态稳定域对车辆进行动态限幅控制能有效降低车辆失稳的可能性。

因此，为解决这些不足，设计了基于动态稳定域的横纵向稳定性协同控制策略。本文结构如下：第1 章介绍所采用的车辆动力学和轮胎模型。第2 章中，首先分析车辆横向稳定性，其次，基于基础稳定域偏移设计动态稳定域，并基于动态稳定域进行动态限幅控制修正稳定域；最后，提出一种辅助前轮转向控制（auxiliary front-wheel steering control，AFC）和DYC 设计动态滑膜横纵稳定控制模型。第3 章中，通过Matlab/Simulink 与CarSim 联合仿真验证所提车辆横纵稳定控制算法的有效性。

1 车辆动力学与轮胎模型

1.1 车辆横向动力学

令、V、V和分别为车辆质量、纵向速度、横向速度和横摆角速度，F(=fl，fr，rl，rr)分别为车辆4 轮横向力，为前轮转角，为从质心到前轮轴距离，为从质心到后轮轴距离，为轮距的一半，F为AFS 产生的侧向力，为DYC 产生的偏航力矩。则四轮车辆动力学模型如图1所示。

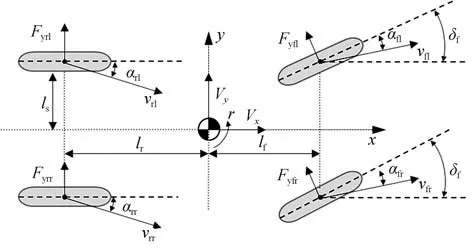
图1 四轮车辆模型

车辆横向稳定性分析和控制设计均采用四轮车辆动力学模型。具有状态变量V和的车辆横向动力学如下所示。

在研究极端条件下车辆横向稳定性，特别是当轮胎侧向力在大侧偏角下饱和时，轮胎横向力不能通过线性近似计算。因此，轮胎侧偏角的计算应与车辆前轮转向角保持相同。

1.2 二维LuGre轮胎模型

本文中采用一种改进的二维LuGre 轮胎模型，其优点是能够准确地描述轮胎的非线性耦合力，且模型参数易于标定。通过改进的二维LuGre 轮胎模型进行侧向力计算。

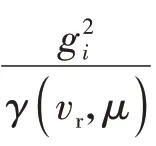
假设路面附着系数可以估计。为保证所提控制方法的有效性，采用与仿真中使用CarSim 轮胎模型相同的LuGre 轮胎模型进行标定，则轮胎模型间的一致性对比如图2所示。

图2 LuGre和CarSim轮胎模型横向力对比

2 动态稳定域分析与稳定控制

2.1 基于投影法的横向稳定性分析

在考虑横纵向稳定性和轮胎特性基础上，本文根据文献［20］和文献［25］中的车辆横向稳定域，分析车辆横向稳定性并设计相应的稳定性控制策略。

通过对车辆操纵稳定性和轮胎稳定性的综合评价，利用局部线性化方法估计得出上图车辆横向稳定域。相较于文献［10］～文献［12］中等其他车辆稳定性评价标准，本文车辆稳定域更为全面。并且，通过合理的控制器设计可保证车辆稳定性和操纵性能。

如图3 所示，在V=25 m/s、=0.75 且=0时，车辆横向稳定域由V-闭合不规则相平面表示。稳定域由4 个边界组成，根据不同车辆操纵稳定性标准，其中两个边界定义为转向过度边界，另两个边界定义为转向不足边界。边界关于原点近似中心对称。稳定域受V、和的影响而变化。

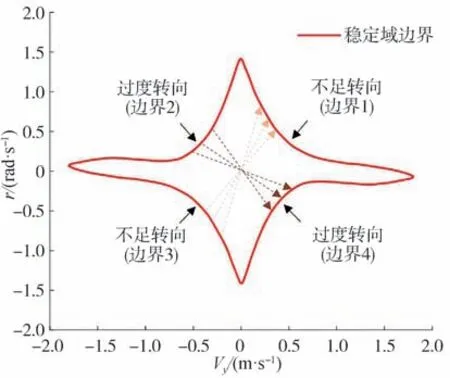
图3 车辆横向稳定域估计［20］

给定上图稳定域，可以通过计算车辆状态点(V，)和区域边界之间的相对距离来分析车辆横向稳定状态。由于稳定域的边界不规则，现有分析方法不适用，因此，提出一种投影法来进行稳定性分析，如图4所示。

图4 投影法与边界最近点

由于边界2 和3 分别与边界1 和4 关于原点对称，因此多项式= f(V)，=1，2 即可描述稳定域边界，在计算最近边界点(V，)时，有

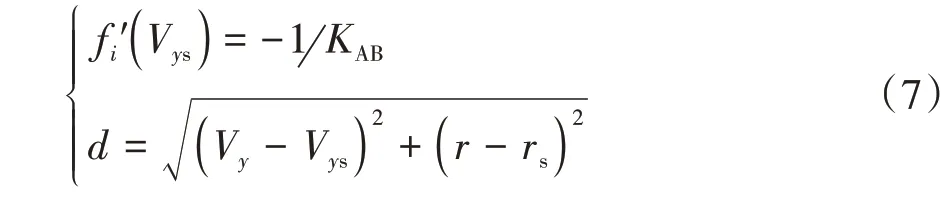
判断车辆失稳方法如表1 所示。稳定域内任意点到稳定域边界最短距离为

表1 基于稳定域的车辆失稳判断方法

2.2 基于基础稳定域偏移的动态稳定域设计

式中和为动态稳定域控制系数，=1.1，=1。横纵向域稳态修正系数、V为

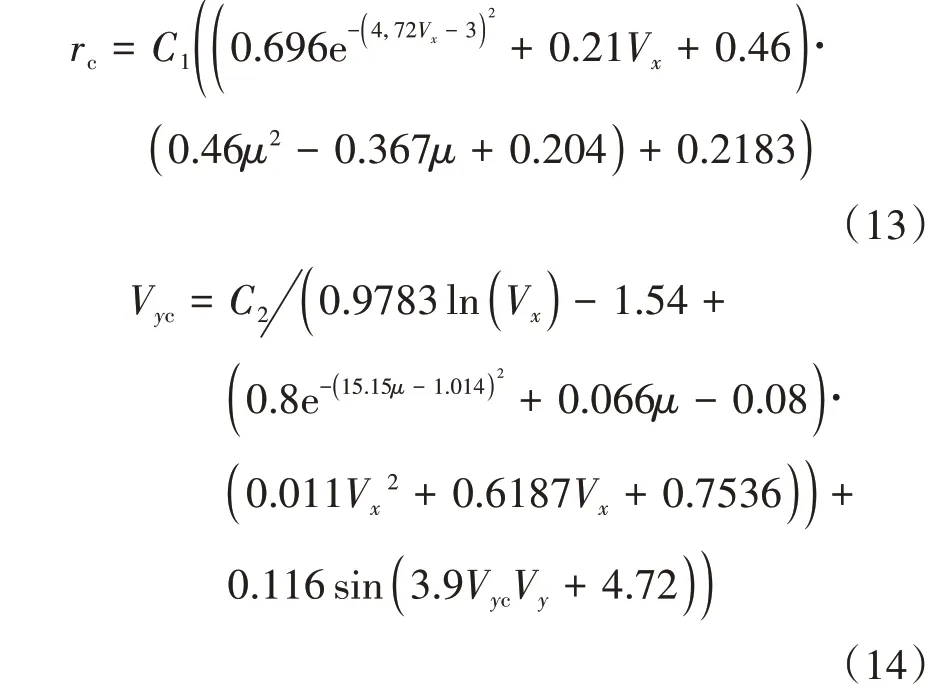
且当V＜0 令V=0。当V和一定时，和V为常数。

为使车辆在临界稳定域仍然可控，通过和将稳定域适当缩小，如图5 所示。和将原动态域适当缩小为虚线所示的动态域。在实际控制过程中，适当的动态域缩小使稳态控制算法提前介入，有利于车辆实时稳定性响应。

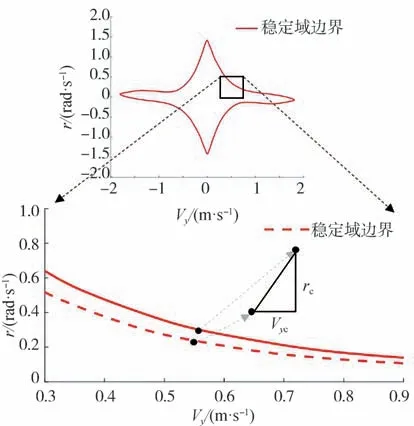
图5 修正的动态稳定域边界

当V和一定时，动态稳定域边界=f(V，V，，)可表示为

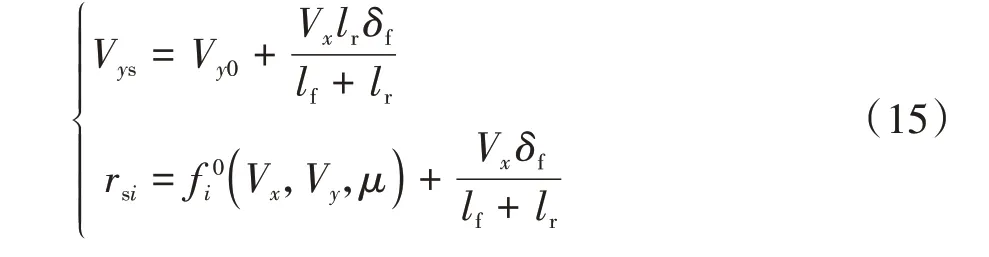
2.3 纵向稳定性限幅控制

平衡点能准确反映车辆的可控状态。若平衡点越趋于离开甚至不在动态稳定域中，则表示越不能回到稳定点。因此，平衡点是否在稳定域内能直接说明车辆的可控性。

图6 不同转角的动态稳定域平衡点

式中为期望前轮转角。则期望减速度：

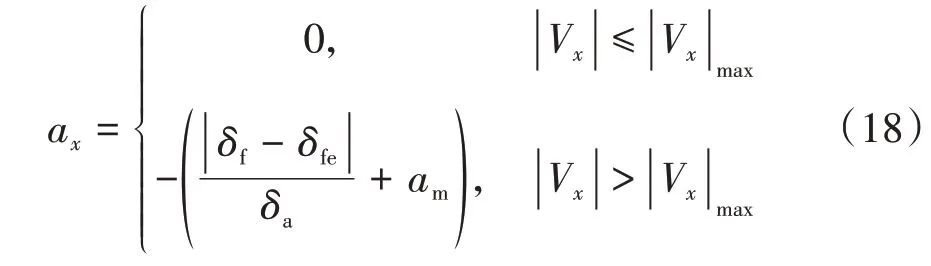
式中：为转角修正系数，间接决定转向角速度；为最小制动常数。

2.4 滑模横纵稳定控制

当不可控因素干扰致车辆失稳，即车辆状态点超出动态稳定域边界时，根据(V，)对车辆进行辅助前轮转角控制和横摆力矩控制，使得车辆趋于稳定状态。

设计滑模面：

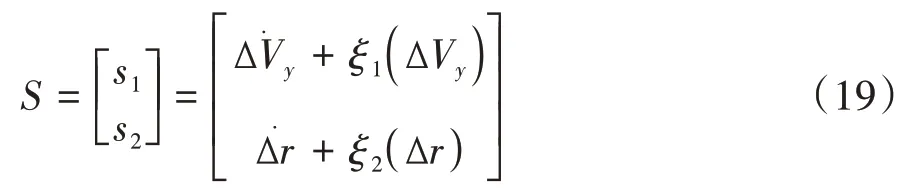
式中和为正常数。

设计趋近率为

定义Lyapunov 函数为=/2 ＞0 并代入式（19）得：

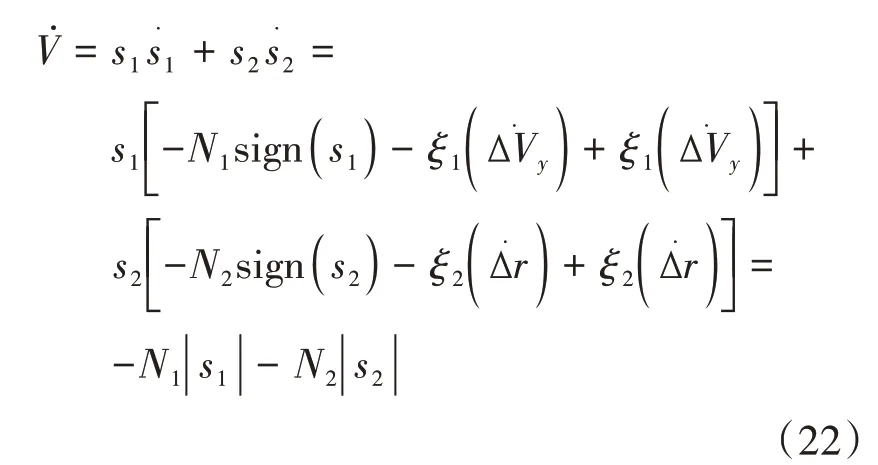
将趋近率代入动力学方程得：

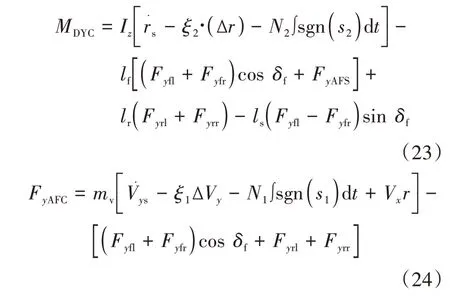
前轮转角主动抵消量：

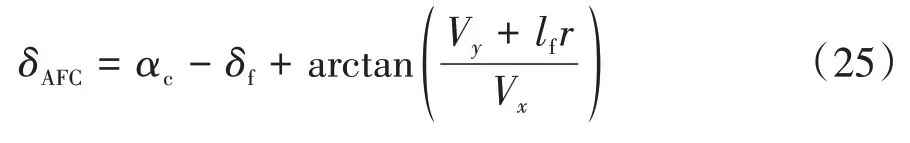
式中：由车辆总横向力F+ F+ F代入轮胎横向力方程反求解出α；δ＜3°。

车身横摆力矩控制4轮制动力：

3 仿真与分析

在横纵向控制过程中，为验证基于动态稳定域的车辆稳定控制设计，分别在Matlab/Simulink 仿真环境中设计高速转向场景和高速双车道轨迹控制场景，联合CarSim进行仿真控制。

表2 车辆和LuGre轮胎模型关键参数

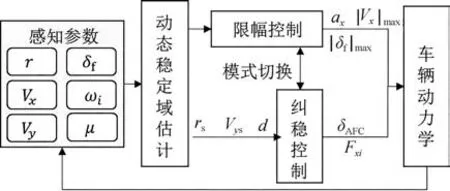
图7 车辆稳定性控制流程

3.1 高速转向稳定控制

车辆高速行驶时，不可靠的转角输入直接影响车辆的横向稳定性。高速转向场景中，通过前轮转角的阶跃输入触发转角限幅控制，使得车辆在安全的前轮转角下进行转向。

设计初始车速为120 km/h，=0.8，对车辆设计的前轮转角输入和实际前轮转角如图8 所示。设计的前轮转角下，若车辆无稳定控制，则会出现因操作不当造成的车辆失控或侧翻；在限幅控制模式下，车辆根据车速计算出允许的极限前轮转角输入。实际车辆稳定域轨迹如图9所示。

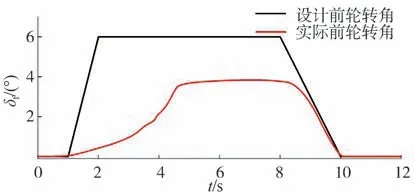
图8 高速转向场景前轮转角输入

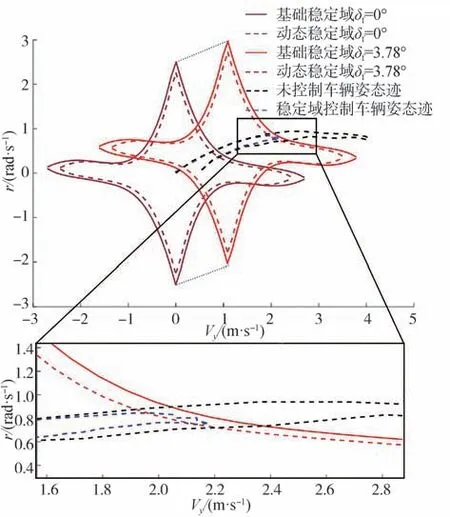
图9 高速转向稳定域轨迹图

稳定域轨迹中，由于在初始速度下无制动和加速控制，动态稳定域边界随车速的缓慢降低略有变化。因此，允许的前轮转角输入动态增加。

3.2 高速双车道轨迹控制

车辆在高速行驶时，若必须按照道路允许的区间行驶，则车辆必须优先满足前轮转角输入控制。仅进行限幅控制无法满足车辆稳定性需求。因此车辆进入纵向协同稳定控制。设计初始车速仍为120 km/h，在期望轨迹下进行前轮转向输入，对车辆进行横纵协同稳定控制。设计前轮转角输入如图10所示。

图10 设计前轮转角输入图

在设计前轮转角输入下，利用动态稳定域约束下的滑膜稳态横纵向控制得出车辆轨迹如图11所示。

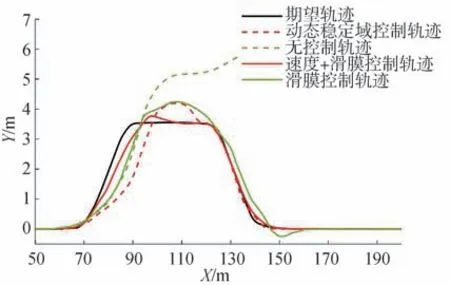
图11 双车道轨迹对比

图11 中，无控制的车辆趋于失控，而基于动态稳定域的滑膜横纵控制的车辆轨迹能良好的满足车辆理想轨迹需求。

图12 为横纵协同稳定控制的实时车速，在期望轨迹下，前轮转角输入后使得纵向控制降低车速，以满足转角的控制需求。

图12 双车道场景稳定控制的实际车速

动态稳定域会随前轮转角和车速的变化而变化，其稳定域边界如图13 所示。图中，无约束的传统滑模控制车辆姿态迹已超出稳定域边界，车辆短暂处于失稳状态。基于动态稳定域的横纵控制姿态迹稳定的处于稳定域边界内，双车道轨迹控制理想。

图13 轨迹控制稳定域图

4 结论

本文中提出一种基于动态稳定域修正的车辆横纵稳定综合控制方法。首先，为分析基于基础稳定域的车辆稳定性状态，提出一种投影法的车辆稳定性分析方法。该分析方法可实时应用于车辆横纵向稳定性控制。其次，根据基础稳定域设计偏移指数的动态车辆稳定域。根据动态稳定域设计纵向加速度控制策略。最后，基于动态稳定域提出AFC 和DYC相结合的动态滑模控制。通过选取以动态裕度为滑膜面的稳定区域边界设计车辆横纵向稳定控制模型，保证了车辆轨迹始终控制在所采用的稳定区域。通过Matlab/Simulink 和CarSim 的联合仿真，验证了基于动态稳定域的车辆横纵向稳定性控制方法的有效性。在实际车辆横纵协同控制应用中，精确的轮胎模型标定直接决定控制模型的有效性和鲁棒性。基于车身垂向稳定性的动态稳定域的控制设计将在今后的工作中完成。