一类具有时滞的两种新冠病毒并行传播的SIR 模型研究

金薇 廖新元 佘智凤

(南华大学数理学院,衡阳,421001)

1 引言

自伊藤给出随机微分方程的概念后,人们发现随机模型相比于确定性模型更具有现实意义,越来越多的学者通过随机微分方程建立传染病模型研究其传播机制[1–4]. Liu Qun 等人考虑到临时免疫和潜伏期,在经典的传染病模型中加入时滞项[5,6]. Wei Ming 等人[7]提出了一类具有潜伏期的两种疾病并行传播的的SIR 模型.

自2020 年以来,2019 新型冠状病毒(2019 nCoV,简称新冠病毒)及它的变异型德尔塔新冠病毒迅速肆虐全球,给人们的生命造成了极大的威胁[8].疫苗接种是预防新冠肺炎最便捷、最有效的手段.考虑到疫苗的时效性和新冠病毒的变异型,本文在[6,7]的基础上建立一个新的新冠病毒SIR 模型.

本文将首先在第二节建立新冠病毒和它的变异型两者并行传播的SIR 模型,然后在第三节通过构造Lyapunov 函数证明此模型全局正解的存在唯一性,并在第四节给出疾病灭绝性和持久性的充分条件,最后在第五节通过数值模拟验证本文的主要结论.

2 模型的建立

自新型冠状病毒肺炎出现到现在为止,虽然很多人都接种了疫苗,但是病毒在传播过程中发生了变异,这无疑给目前的研究带来了很大的困扰.考虑到疫苗的时效性和病毒的变异型,本文建立如下的SIR 模型:

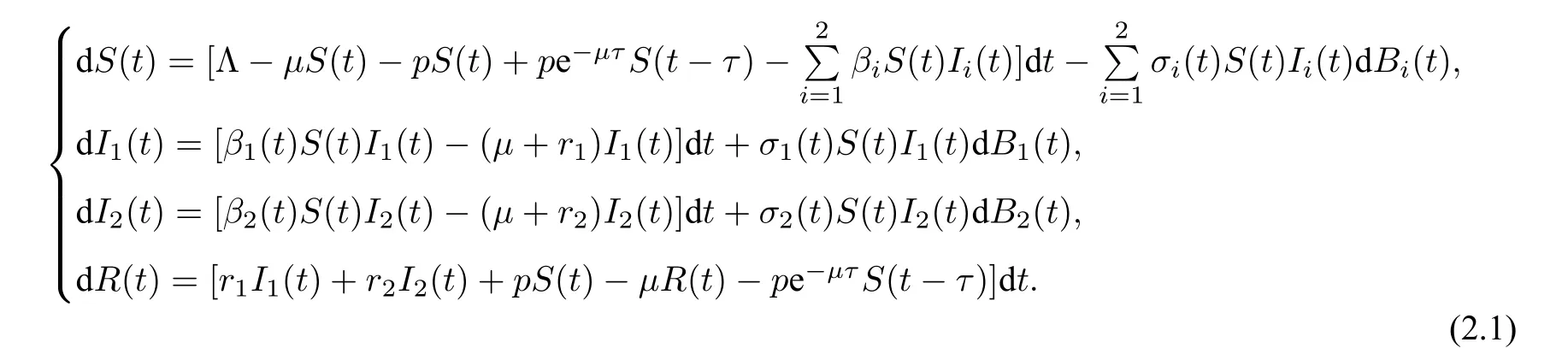
其中S(t),I1(t),I2(t),R(t)分别表示在t时刻的易感者数量、未变异的新冠病毒感染者数量、变异型新冠病毒感染者数量和免疫者数量;参数Λ,µ分别表示人群总体的出生率和死亡率,p表示疫苗接种率,β1,β2分别表示新冠肺炎与其变异型的传播系数,r1,r2分别表示患该两种肺炎人群的恢复率;τ表示疫苗的有效期,在t −τ时刻接种过疫苗的易感者在t时刻丧失免疫力再次成为易感者,由于这部分人群仍存在死亡率,故其在t时刻还活着的概率是e−µτ.

由模型(2.1)可得

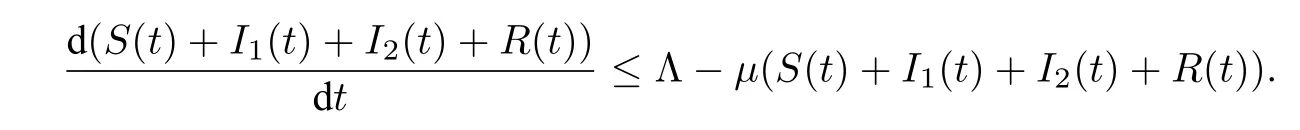
故

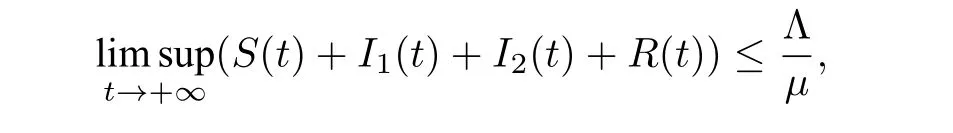
即

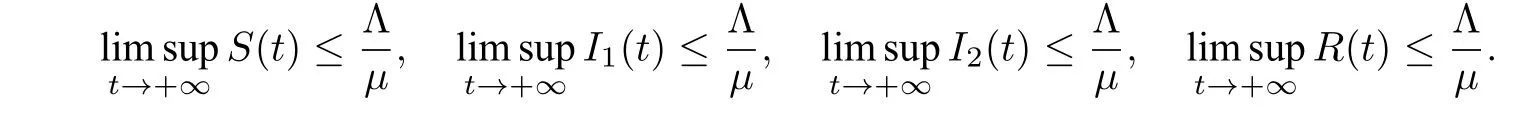
注意到前三个方程不依赖第四个方程,不失一般性,我们仅讨论由前三个方程构成的简化模型.

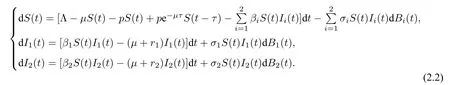
令(Ω,F,{F}t≥0,p)表示带有滤子{F}t≥0,p且满足通常条件(单调递增、右连续且包含所有的P 零集)的全概率空间.对区间[0,∞)上的可积函数f(t),定义〈f(t)〉=f(s)ds,t>0.

3 全局正解的存在唯一性

定理3.1对于任意的初值(S(0),I1(0),I2(0)),模型(2.2)依概率1 存在全局唯一正解.

证明由于模型(2.2)的系数满足局部Lipschitz 条件,因此对于任意初值(S(0),I1(0),I2(0)),模型(2.2)存在一个局部解(S(t),I1(t),I2(t)),t ∈[−τ1,τe),其中τe是爆破时刻.要证明此解是全局的, 只需证明τe=∞. 为此, 取n0充分大, 使得(S(0),I1(0),I2(0))∈[,n0]. 对任意正整数n>n0,定义停时

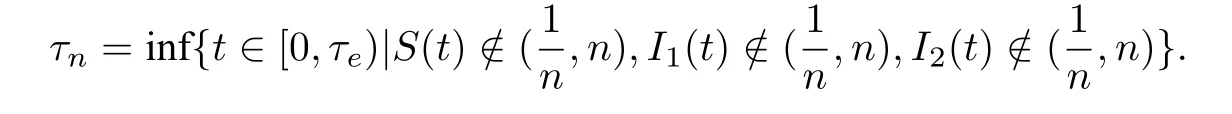
当n增大时,τn是递增的.令τ∞=τn. 接下来证明τ∞=∞.利用反证法,假设τ∞<∞,则存在正整数T>0 和ε ∈(0,1),使得

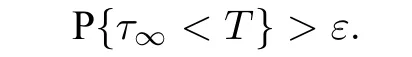
从而,存在正整数n1>n0,使得

定义如下的C3函数V:→R+:

由It^o 公式可得

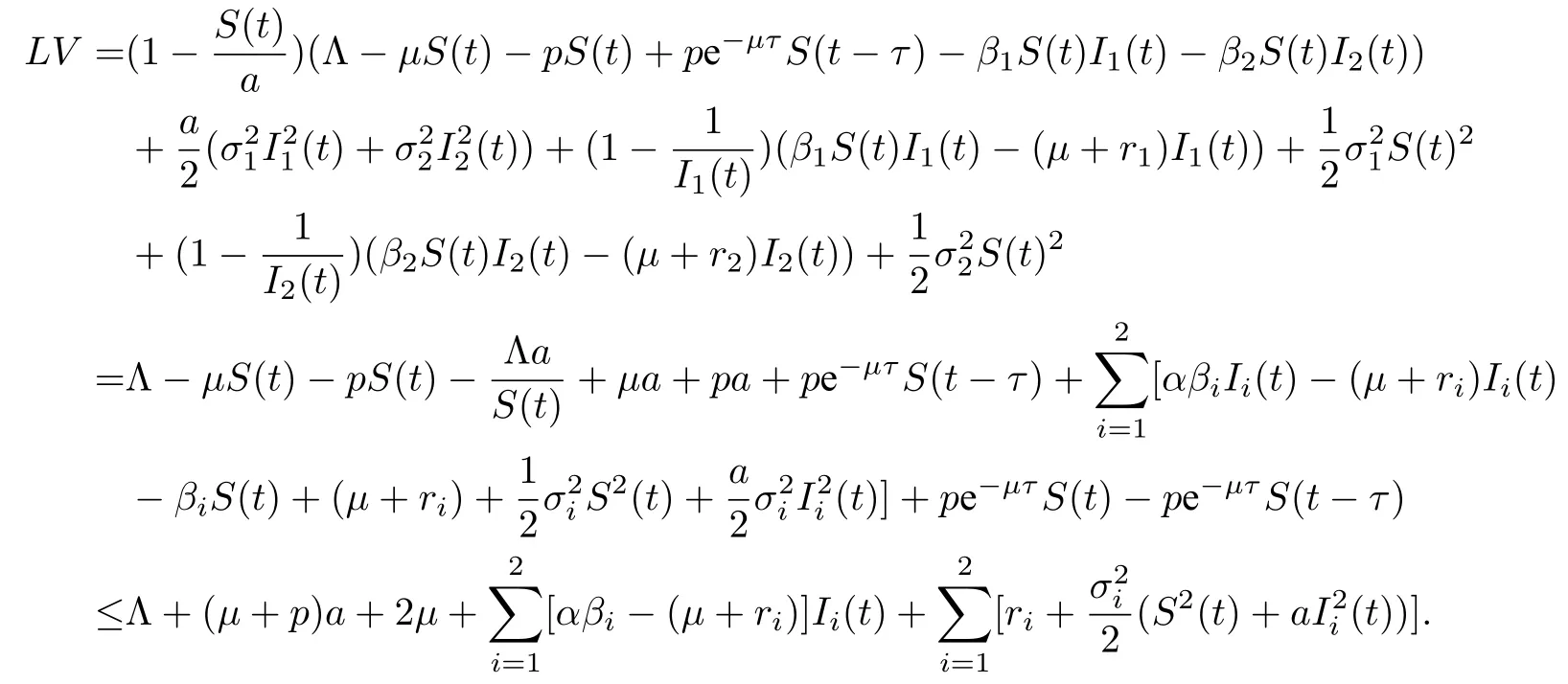
取a=min{},则αβi ≤µ+ri(i=1,2). 因此

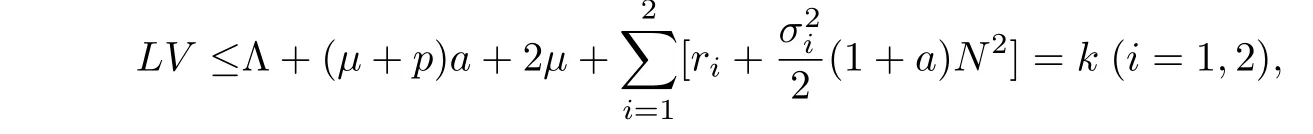
其中k>0 是一个常数.从而

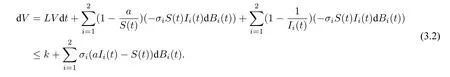
对(3.2)式两边同时从0 到τn ∧T积分,并取期望得

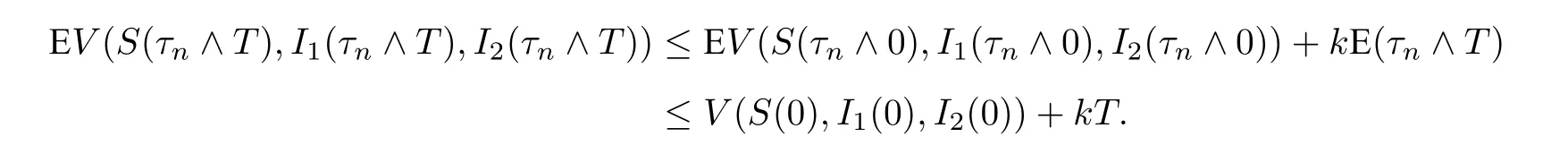
令Ωn={τn ≤T},n ≥n1.由(3.1)式可知,P(Ωn)≥ε.注意到对每个ω ∈Ωn,有S(τn,ω)或I1(τn,ω)或I2(τn,ω)等于或n,且pe−µτS(s)ds恒为正,因此

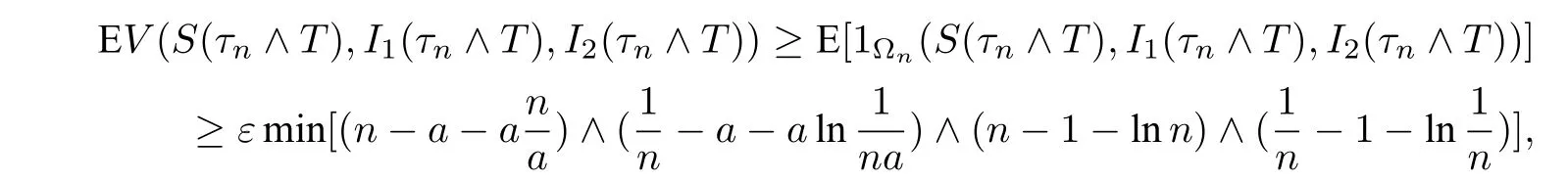
其中1Ωn是Ωn的示性函数.

令k →∞得

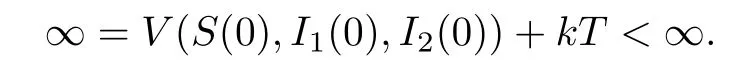
这不可能成立,因此假设不成立,故τ∞=∞.定理3.1 证毕.

4 疾病的灭绝性和持久性

4.1 疾病的灭绝性

引理4.1([9]) 设M={Mt}t≥0是M(t)=0 的实值连续局部鞅.则有

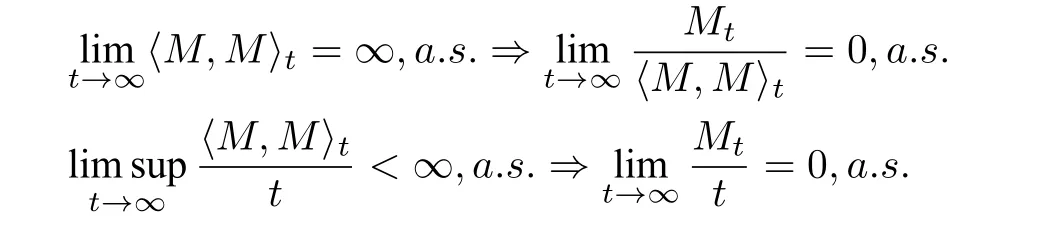
定理4.1设(S(t),I1(t),I2(t)) 是初始值为(S(0),I1(0),I2(0)) 的模型(2.2) 的解. 若R1<1,R2< 1,≤min{}(i= 1,2),a.s.成立, 则I1(t) =I2(t)=0.其中

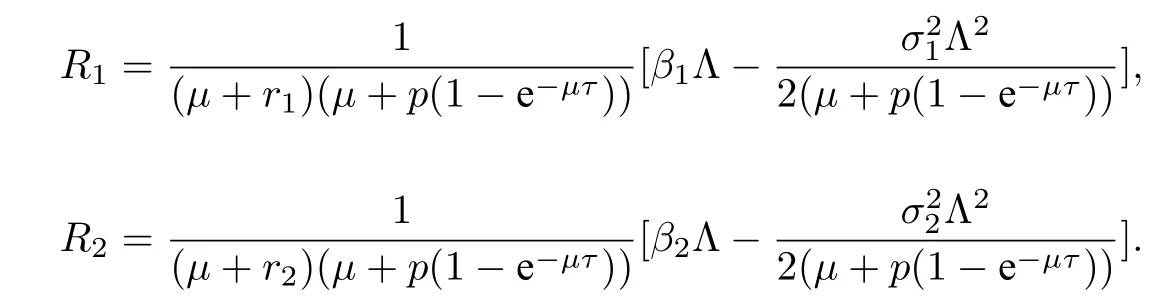
证明由模型(2.2)可得

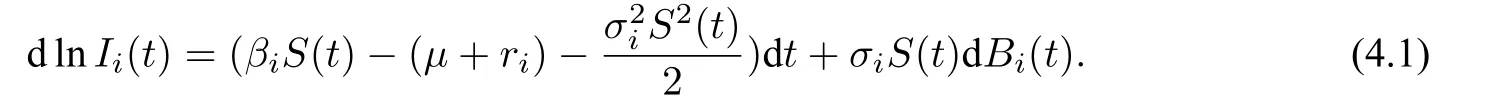
将(4.1)式两边从0 到t积分,再除以t得

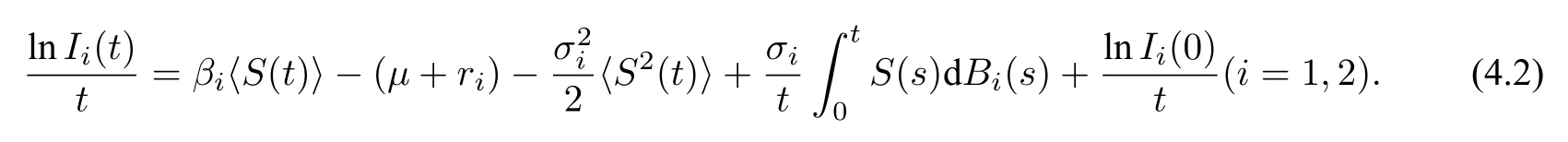
对上式两边从0 到t积分,再除以t得

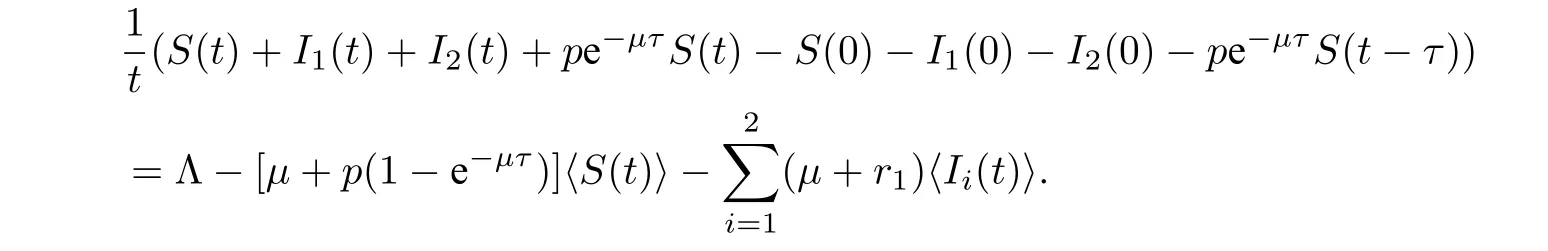
故

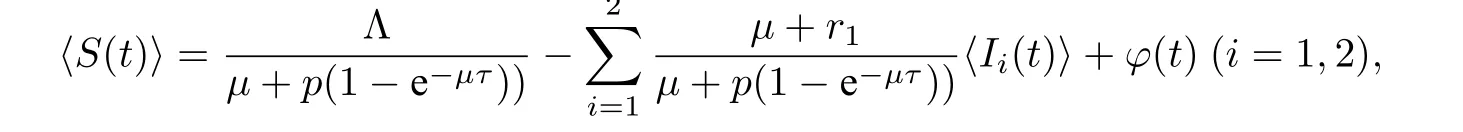
其中

其中

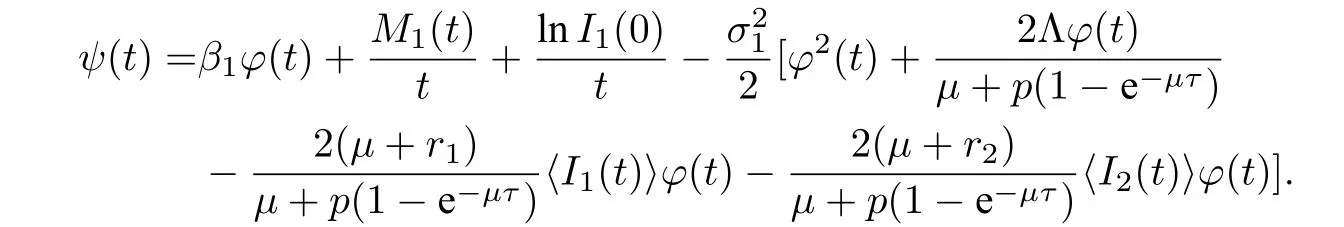
由(4.3)式可得

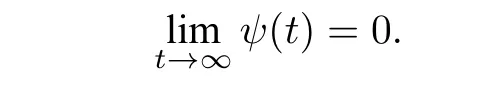
若

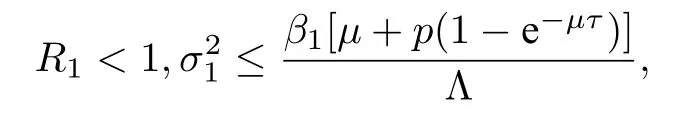
则

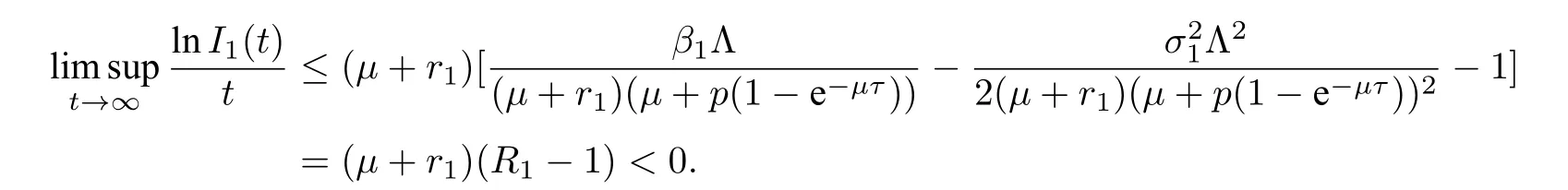
4.2 疾病的持久性

定理4.2设(S(t),I1(t),I2(t))是初始值为(S(0),I1(0),I2(0))的模型(2.2)的解. 若

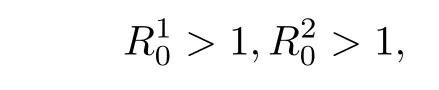
则新冠肺炎及其变异型都持久,且I1(t)和I2(t)满足

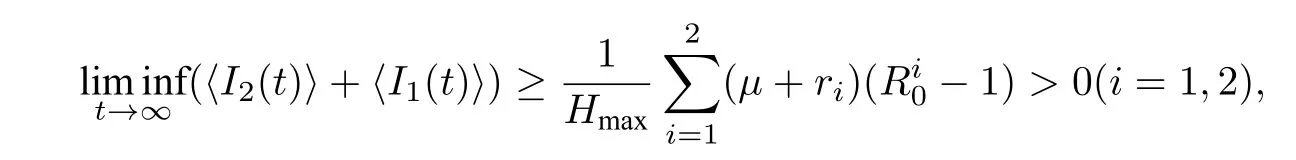
其中

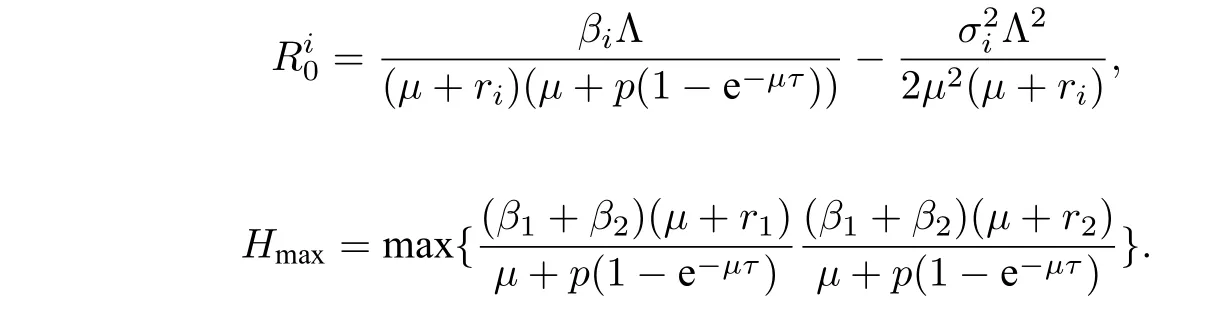
证明 定义V1=lnI1(t)+lnI2(t).由It^o 公式可得

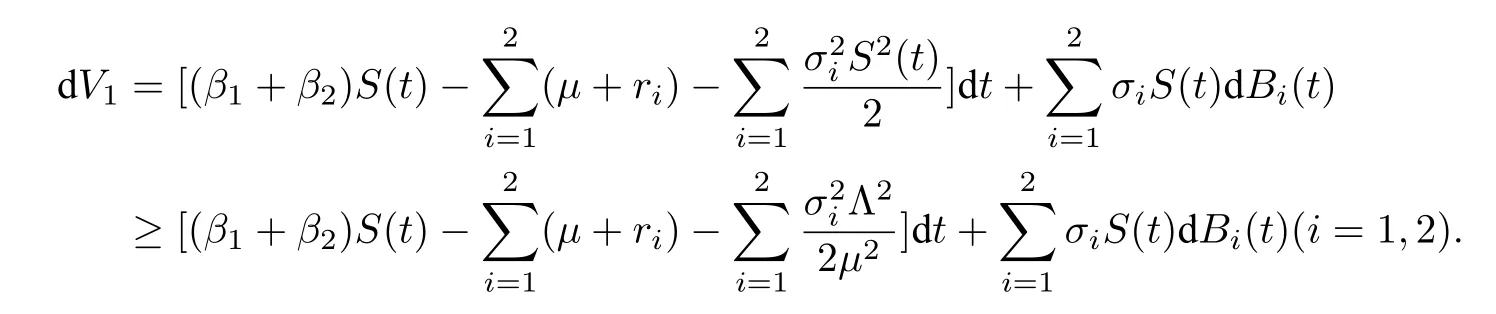
将上式两边从0 到t积分,再除以t得

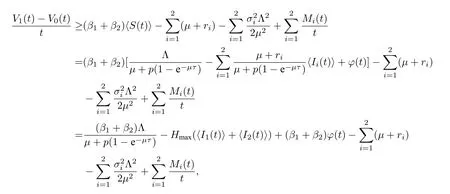
其中

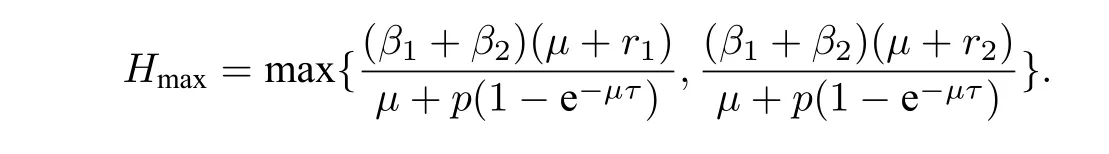
故

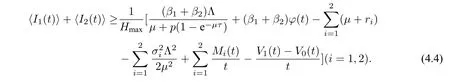
又

对(4.4)式取极限便得

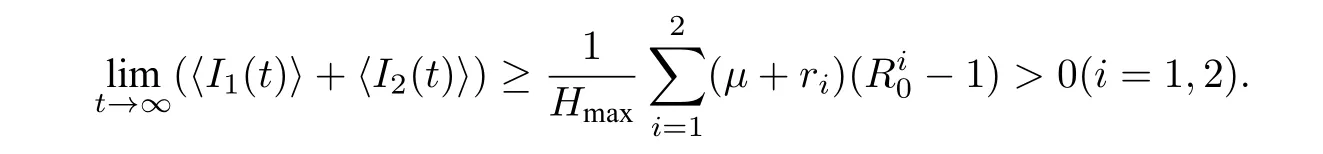
定理4.2 证毕.

5 数值模拟

利用Euler Maruyama 方法[11]对本文的SIR 模型进行数值模拟,从而验证主要结论.参考文献[12,13],对本文参数进行取值.

1.取Λ = 0.25,µ= 0.18,p= 0.25,β1= 0.45,β2= 0.55,r1= 0.15,r2= 0.5,σ1= 0.25,σ2=0.2.计算可得R1=1.42,R2=0.877,=1.359,=0.858,≤0.398,≤0.487.此时新冠肺炎持久,而其变异型灭绝,如图1 所示.

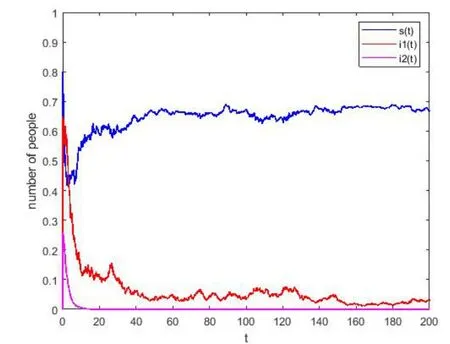
图1 新冠肺炎持久而其变异型灭绝

2.取Λ = 0.25,µ= 0.18,p= 0.25,β1= 0.45,β2= 0.55,r1= 0.35,r2= 0.15,σ1= 0.25,σ2=0.2.计算可得R1= 0.884,R2= 1.806,= 0.846,= 1.767,≤0.398,≤0.487.此时新冠肺炎灭绝,而其变异型持久,如图2 所示.

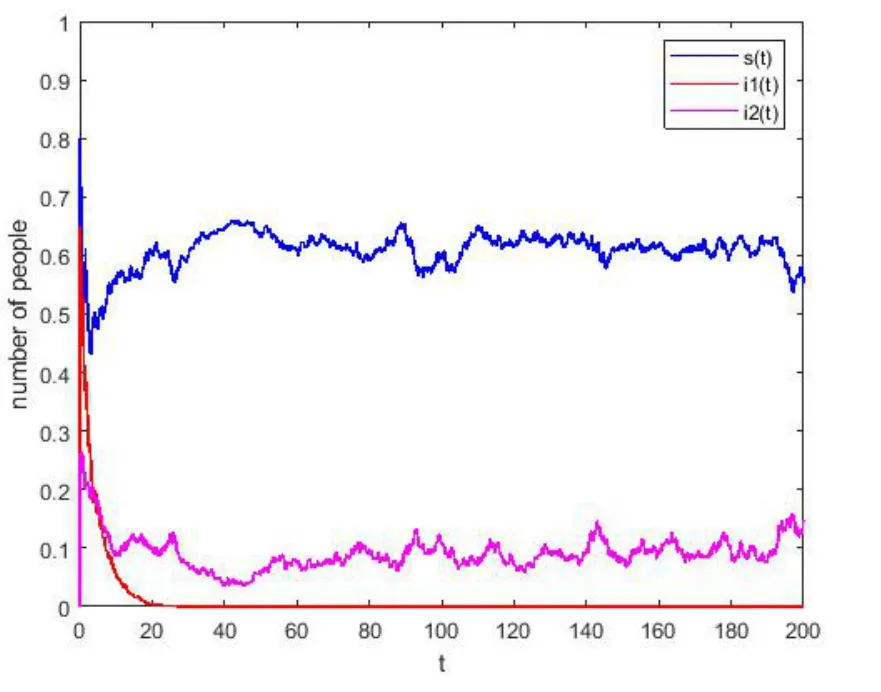
图2 新冠肺炎灭绝而其变异型持久

上述结果表明:当R1<1 且R2<1 时,新冠肺炎及其变异型灭绝.当>1 且>1 时,新冠肺炎及其变异型持久.这与定理4.1 和定理4.2 的结论相符.

3.保持情形1 的其他参数不变,让σ1从0.25 增大至0.68,则R1=0.646,=0.19,此时新冠肺炎由持久变为灭绝,而其变异型的灭绝性不变.如图3 所示.

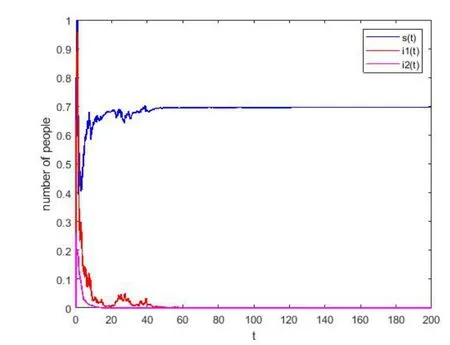
图3 σ1 =0.68 时,新冠肺炎及其变异型均灭绝

4.保持情形2 的其他参数不变,让σ2从0.2 增大至0.7,则R2= 0.935,= 0.452,此时新冠肺炎的灭绝性不变,而其变异型由持久变为灭绝.如图4 所示.

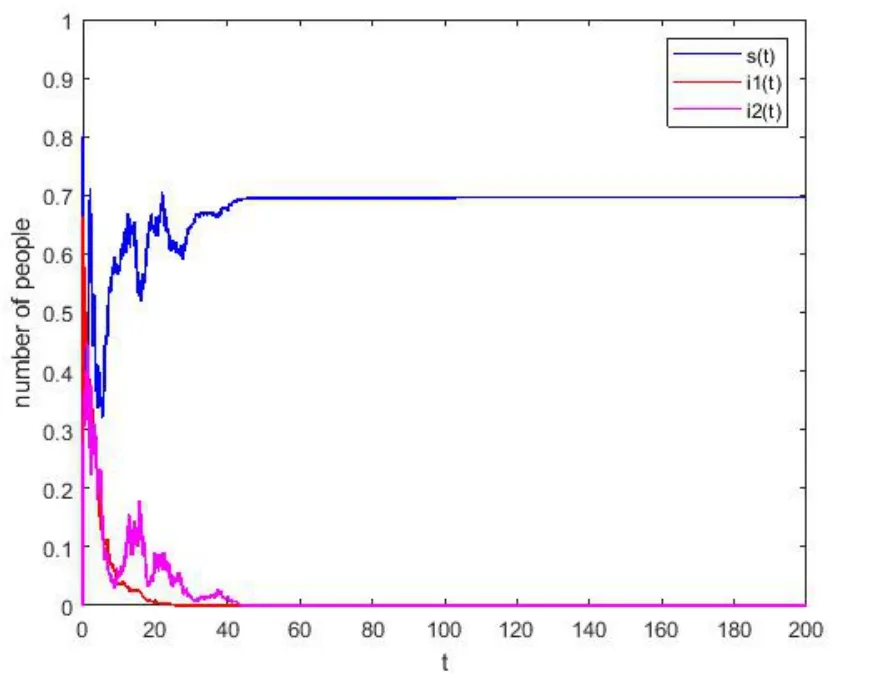
图4 σ2 =0.7 时,新冠肺炎及其变异型均灭绝

综上可知:噪声强度越大,新冠肺炎及其变异型灭绝的时间越短.这说明环境干扰有利于控制疾病传播.