适用于高压直流输电的组合型基频开关主动换相换流器功率因数控制策略研究

栾轲栋，李耀华，李子欣，赵 聪，王 平

(1.中国科学院电力电子与电气驱动重点实验室，中国科学院电工研究所，北京 100190；2.中国科学院大学，北京 100049)

1 引言

基于晶闸管的电网换相换流器(Line Commutated Converter，LCC)[1,2]高压直流输电技术(High Voltage Direct Current，HVDC)，具备传输容量大、输电走廊面积小、适用于异步电网互联、器件串联均压技术较为成熟等优点。但是，由于晶闸管属于半控型功率半导体器件，其开通时刻和关断过程均受到外部电路条件的约束，即LCC的触发角滞后于自然换相点，使得LCC传输的有功功率和无功功率之间相互耦合，无法实现独立控制，交流侧需配置大量的无功补偿和滤波装置。此外，LCC无法实现黑启动，且存在换相失败风险[3]。在风电和光伏等新能源并网输送以及孤岛供电等领域，LCC的应用受到了严重限制。

相比于LCC技术，电压源型换流器(Voltage Source Converter，VSC)选用全控的功率半导体器件，基于VSC的高压直流输电技术灵活性和可控性更强[4]，不存在换相失败风险，具备黑启动能力，可实现有功和无功功率解耦控制，便于构建直流电网。高压直流输电场合，两电平和三电平VSC存在器件串联均压困难、谐波含量大、dv/dt引起的电磁干扰严重且运行效率较低等问题[5]。随着模块化多电平换流器(Modular Multilevel Converter，MMC)的发明，基于MMC的VSC-HVDC以其结构模块化、谐波含量低、可靠性高以及效率高等诸多优点获得了广泛应用[6-8]，已经成为VSC-HVDC技术中的主流方案，并在国内外多个HVDC工程获得应用。尽管如此，MMC自身仍存在一些问题和不足，MMC除了需要使用数量较多的功率半导体器件之外，对子模块储能电容要求较高[9,10]，使得MMC体积及重量大，需要采用阀塔安装的形式，且造价相对昂贵。全桥型MMC或者由半桥子模块和全桥子模块混合的MMC相对于半桥型MMC能够实现直流短路故障自清除，但是使用的功率半导体器件数量更多，进一步增加了成本。

主动换相换流器(Actively Commutated Converter，ACC)和LCC的电路拓扑较为类似，本质上也属于电流源型换流器[11]。不同的是，ACC采用可自关断的全控逆阻型功率半导体器件，其开通和关断不再受外部电路条件的限制，因此ACC不存在换相失败的风险、具备黑启动的能力，能够向无源网络供电、实现有功功率和无功功率的解耦控制，且交流侧所需的无功补偿装置和滤波器也相对较少[12,13]。相对于MMC，ACC使用的功率半导体器件较少，且无需大量的储能电容，可以减轻换流阀的重量，采用悬挂安装的形式，相对地减小换流站的体积和占地面积，降低工程成本。此外，ACC同样可以灵活控制直流侧电压、电流，具备直流短路故障抑制能力。

在高压直流输电场合，ACC换流阀的桥臂可采用一定数量的自关断逆阻型功率半导体器件串联构成，其中，自关断逆阻型功率半导体器件可以是压接式对称型IGCT/IGBT或由压接式非对称型IGCT/IGBT与二极管串联组成[14]。功率半导体器件串联使用时，存在功率半导体器件静态、动态均压问题，ACC的开关频率受到一定的限制[15]。目前，相关文献对于ACC在HVDC系统的应用也开展了一定的研究，文献[16]对一端采用LCC、一端采用ACC 的背靠背混合直流输电系统进行了研究，并对其功率传输特性、基本控制策略、启动方法、潮流翻转策略和故障工况下的控制策略进行分析和设计；文献[17]针对ACC 的有功功率与无功功率耦合关系复杂导致功率因数难以控制的问题，提出一种基于dq 坐标系的间接电流控制方法，实现了有功功率和无功功率的解耦控制，并分析了变流器的稳定运行范围，指出了ACC 无功功率受限于有功功率的原因；为了降低开关频率的同时降低输出电流的谐波含量；文献[18]提出了一种根据“虚拟相电流”对应的二值逻辑“虚拟触发信号”生成ACC实际触发信号的特定谐波消除调制方法(Selective Harmonic Elimination，SHE)，能够在不同调制度下保持开关信号类型的一致性，有效消除特定次谐波，开关频率降低到350 Hz；文献[19]基于SHE的思想提出了一种适用于九电平ACC的调制策略，实现了ACC基频开关调制，但是其中每台并联的三电平ACC触发控制时刻相互关联，无法实现每台ACC触发时刻独立，实现较为复杂；文献[20]提出通过移相的方法实现ACC基频开关运行并减小交流侧谐波，并没有考虑交流侧参数对于网侧功率因数的影响；文献[21]提出了基频开关ACC的直流输电系统协调控制方法和功率运行范围，并与PWM工作模式下的功率运行范围进行了对比。

本文针对由两台ACC直流侧串联、交流侧并联组成的组合型ACC，提出一种开关频率为50 Hz的基频开关高功率因数运行方法。与LCC不同，基频开关ACC的触发时刻不受外部电路条件约束，具备触发角超前和触发角滞后两种工作模式，使得组合型基频开关ACC具备调节有功功率和无功功率的能力，能够工作在高功率因数运行状态。此外，本文分析了基于电网电压定向时ACC的功率传输特性，在此基础上，为了进一步提高网侧功率因数，引入功率因数补偿角对基频开关ACC的触发角进行调整，使组合型基频开关ACC的网侧运行在单位功率因数附近。仿真和实验结果均验证了本文理论分析及所提出的功率因数控制方法的正确性和有效性。

2 组合型基频开关ACC及控制方法

2.1 组合型基频开关ACC

组合型基频开关ACC的基本电路拓扑如图1所示，组合型基频开关ACC由两台三电平ACC模块交流侧并联、直流侧串联构成。每台三电平ACC模块由6个桥臂构成，上、下两个桥臂构成一个相单元。两台三电平ACC模块的高压直流侧通过直流滤波电抗器Ldc串联连接，交流侧通过两台变压器并联连接后经过二阶LC滤波电路连接交流电网。

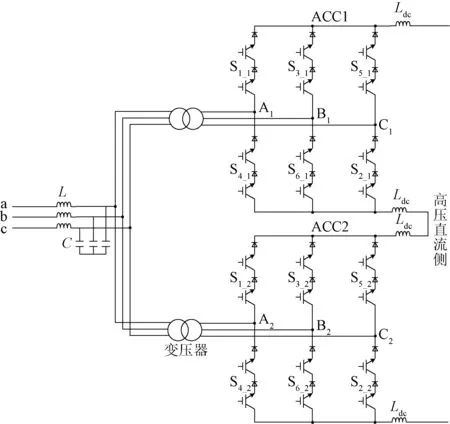
图1 组合型基频开关ACC电路拓扑Fig.1 Combined ACC with switching frequency of 50 Hz circuit topology

以图1所示的三电平ACC模块为例，正常工作时，ACC某一相单元的上桥臂导通、下桥臂关断时，该相输出的电流为Idc，记为状态1；上桥臂关断、下桥臂导通时，该相的输出电流为-Idc，记为状态-1；上、下桥臂的开关管同时导通或关断时，该相输出电流为0，记为状态0。不考虑叠流时间，ACC的开关约束条件为三相上下桥臂中有且仅各有一个桥臂处于导通状态，开关状态sk和开关约束条件可以表示为：

(1)

sa+sb+sc=0

(2)

ACC工作在50 Hz开关模式下，为满足开关约束条件式 (2)，在每个开关周期T内，每个桥臂导通时间均为T/3。根据导通桥臂所处的位置，将ACC一个开关周期T内的开关状态分为六种，六种开关状态轮换交替，每个开关状态持续时间为T/6。

50 Hz开关模式下，ACC的导通桥臂轮换顺序与LCC桥臂轮换次序相似，可以参考LCC触发角控制的工作模式。与LCC不同的是，ACC使用可自关断的全控型功率半导体器件，器件的开关和关断时刻不再受到外部电路条件的限制，即ACC的触发角起始时刻可以与LCC一样滞后于自然换相点，称为滞后触发模式，此外，ACC的触发角起始时刻还可以超前于自然换相点，称为超前触发模式。

以交流侧线电压Uac的过零点作为自然换相点，此时刻记为零时刻。滞后触发模式下，触发角为α时，1号开关状态导通桥臂S6、S1起始时刻对应的角度为α，结束时刻对应的角度为60°+α，以此类推可以得到滞后触发模式下其他5种开关状态的导通角度。同样地，超前触发模式下触发角为α时，1号开关状态导通桥臂S6、S1起始时刻对应的角度为-α(即360°-α)时，结束时刻对应的角度为60°-α，同样可以推导出超前触发模式下其余5种开关状态的导通角度。基频开关ACC的开关状态对应的导通桥臂以及导通角度见表1。

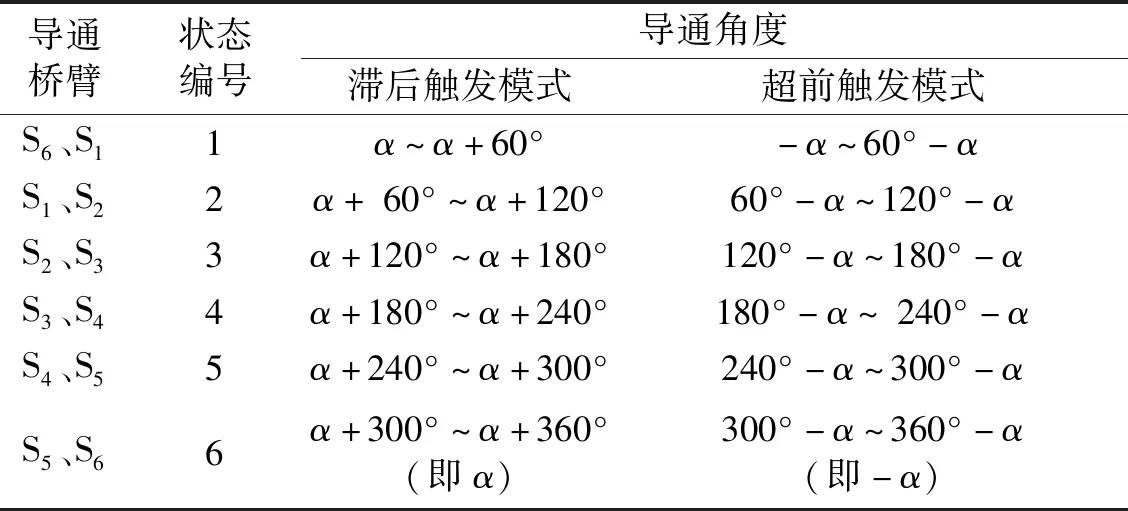
表1 基频开关ACC开关状态Tab.1 Switch state of ACC with switching frequency of 50 Hz

以图1所示的组合型基频开关ACC的a相输出电流为例进行说明，其中直流电流为Idc，ACC1采用滞后触发模式，ACC2采用超前触发模式。

ACC1和ACC2的a相输出电流分别如图2(a)、图2(b)所示，ACC1和ACC2输出电流IACC1、IACC2中基波含量可以用式(3)、式(4)表示：

(3)

(4)

式中，θ为交流侧线电压Uac的相位；α为触发角。

组合型基频开关ACC的a相输出电流IACC为ACC1和ACC2输出电流之和，如图2(c)所示，其中的基波分量如式(5)所示：

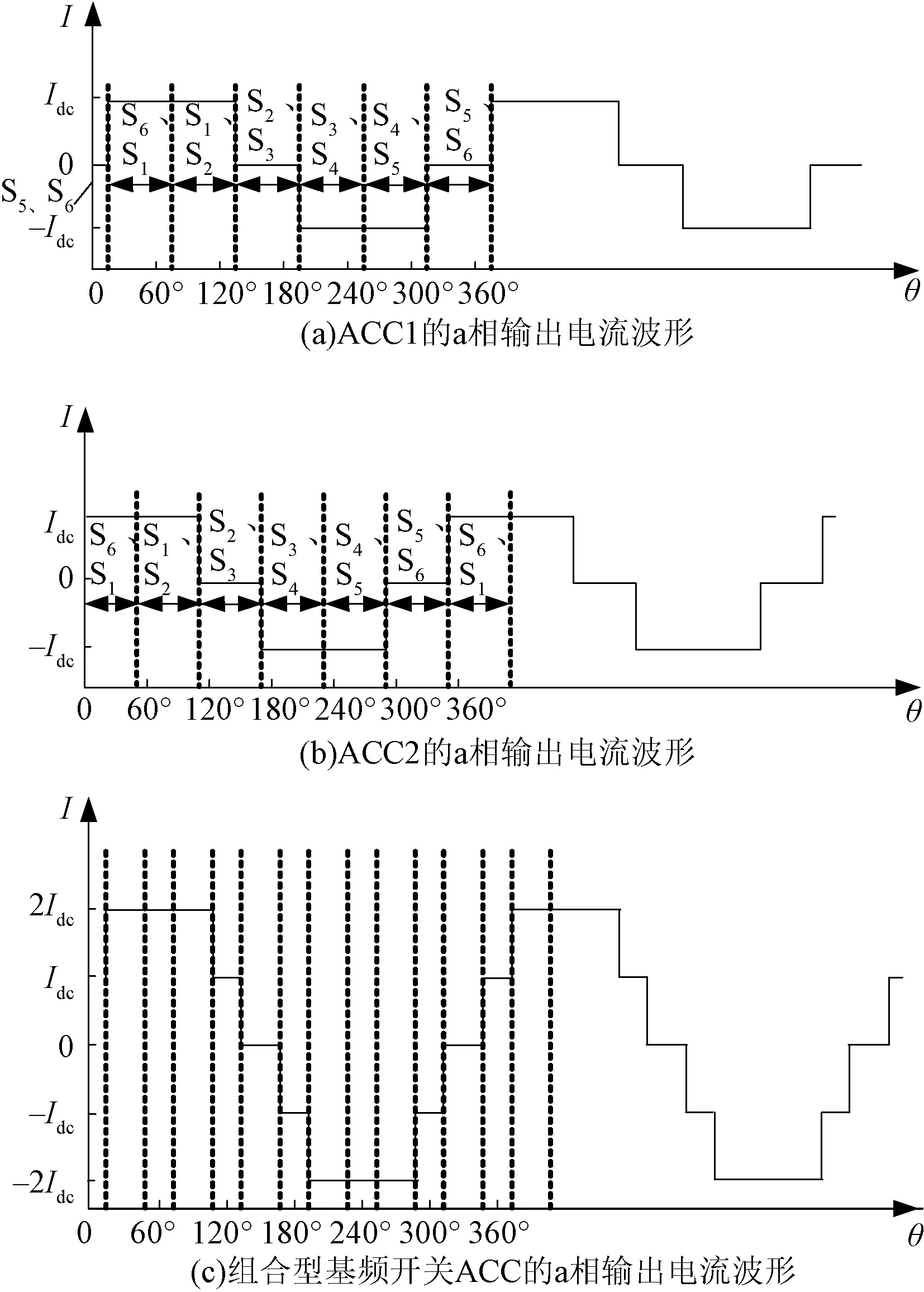
图2 组合型基频开关ACC输出电流波形Fig.2 Output current wave of combined ACC with switching frequency of 50 Hz

(5)

可以看出，组合型基频开关ACC输出电流的基波含量相位与触发角α大小无关，超前于交流侧线电压Uac的相位π/6，即组合型基频开关ACC交流侧输出电流能够与交流侧相电压保持同相位。基波含量幅值与触发角α的余弦值大小正相关。

组合型基频开关ACC工作在上述工作模式时，一个开关周期内，模块ACC1、ACC2的开关导通状态及直流侧电压Udc1、Udc2见表2，其中vij为ACC交流侧线电压。

从表2中可以看出，ACC1和ACC2的直流侧电压均为6脉波，组合型基频开关ACC的直流侧电压为12脉波，是ACC1、ACC2直流侧电压之和。一个周期内，组合型基频开关ACC直流侧电压Udc的平均值用式(6)表示，其中Uline为交流侧线电压幅值。

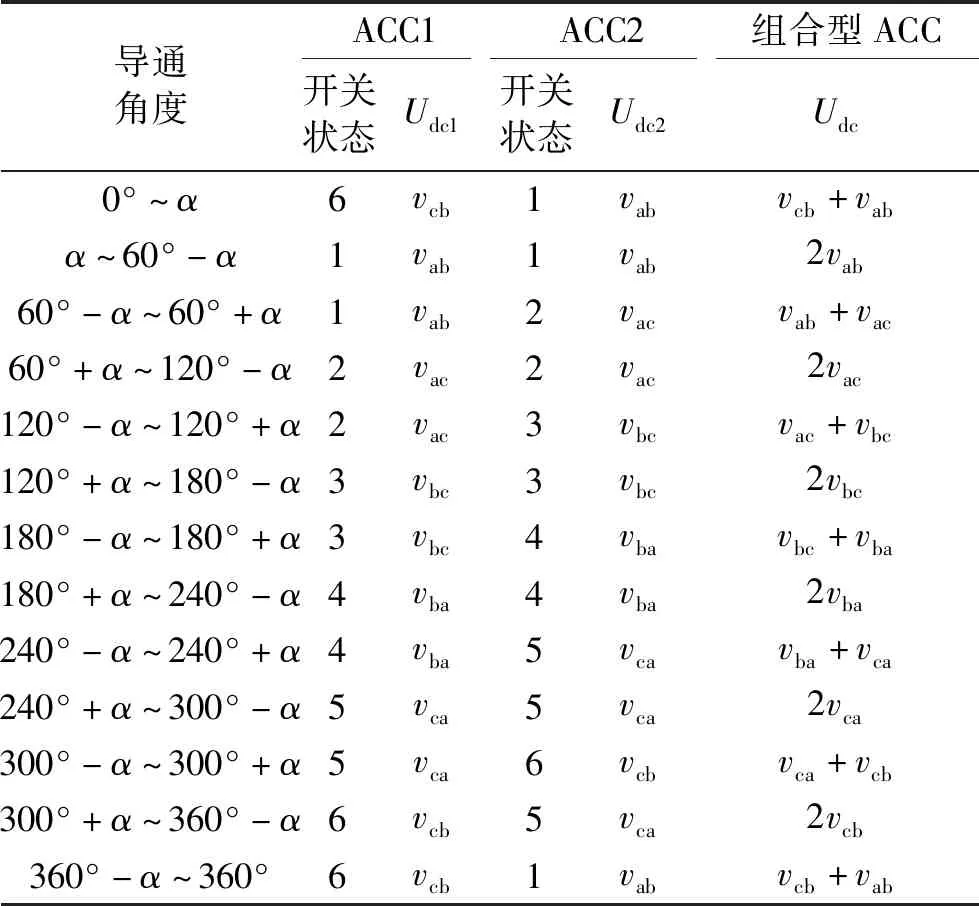
表2 组合型基频开关ACC工作状态Tab.2 Switch state of combined ACC with switching frequency of 50 Hz

(6)

2.2 直流侧电压控制

组合型基频开关ACC的直流电压控制框图如图3所示，直流电压控制环将采集到的直流电压Udc_measure与直流电压给定值Udc_ref比较，通过PI控制器调节得到触发角，ACC1采用滞后于过零点触发，ACC2采用超前于过零点触发，从而直接控制直流电压Udc的大小。

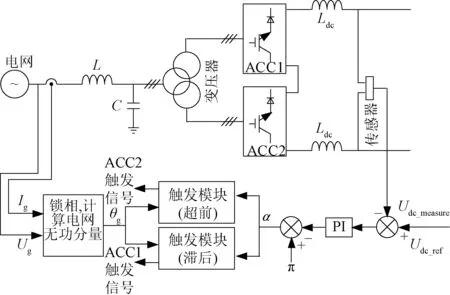
图3 组合型基频开关ACC控制框图Fig.3 Control block diagram of combined ACC with switching frequency of 50 Hz

典型的组合型基频开关ACC的电路拓扑如图1所示，其中交流侧的三相LC滤波器，一方面可以滤除组合型基频开关ACC输出电流的高次谐波，另一方面还具有辅助ACC开关器件换流的功能。

首先定义d-q坐标系下变量X=Xd+jXq，根据KVL和KCL，可以得到d-q坐标系下组合型ACC交流侧电压电流之间的关系：

Ug=UC+UL

(7)

Ig=Iout+IC

(8)

式中，Ug、Ig分别为交流侧电网电压、电流；IC、UC分别为交流滤波电容C的电流、电压；UL为交流滤波电感L两端电压；Iout为组合型ACC输出电流。

基于电网电压定向的同步旋转坐标系中，根据式(7)、式(8)画出d-q坐标系下各变量间的关系如图4所示。

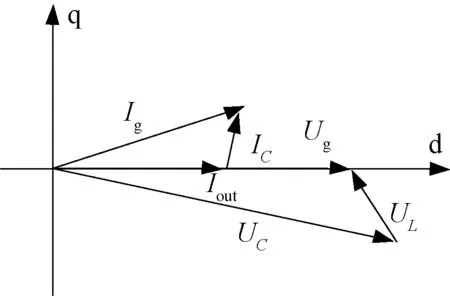
图4 基于电网电压定向的ACCFig.4 Diagram of ACC based on grid voltage orientation

如图4所示，传输功率时换流阀直接相连的滤波电容电压UC的相位和交流电网电压Ug相位存在差异，由于电容电流IC的作用，使得系统具有超前的功率因数。

组合型ACC的交流侧等效电路拓扑如图5所示，基于基尔霍夫定律可以得到：

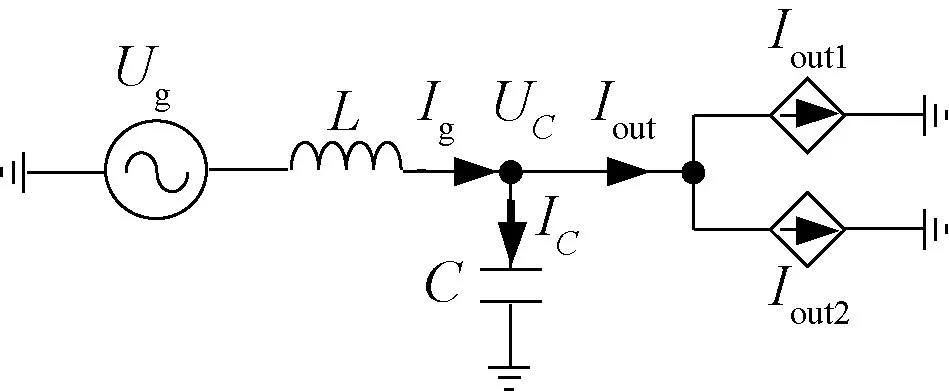
图5 组合型ACC的交流侧等效电路拓扑Fig.5 AC side equivalent circuit topology of combined ACC

(9)

式中，ω为电网电压角频率。

交流侧电网电流Ig、电容电压UC与组合型ACC输出电流Iout、电网电压Ug和交流侧LC滤波参数之间的关系可以表示为：

(10)

组合型ACC的两台ACC触发信号分别为α1和α2时，组合型ACC输出电流Iout为两台ACC的输出电流Iout1、Iout2之和：

(11)

结合式(9)～式(11)，可以得到电网电流Ig和电容电压UC：

(12)

式中，θC为电容电压UC的相位。

由式(6)可知，直流侧电压只受到触发角控制，基于电网电压锁相时，ACC触发角计时零点为交流侧电网线电压Ug_line的过零点，此时，ACC1和ACC2的直流侧电压分别为：

(13)

式中，UC_line为交流侧电容线电压有效值，式(13)可以看出基于电网电压锁相时，ACC1和ACC2的直流侧电压存在差异。

2.3 组合型基频开关ACC网侧功率因数控制方法

图6为在上述分析的基础上，引入了功率因数补偿角，强迫组合型ACC交流输出电流Iout的q轴分量与电容电流IC的q轴分量相抵消，这样可以实现交流电网侧的单位功率因数运行。

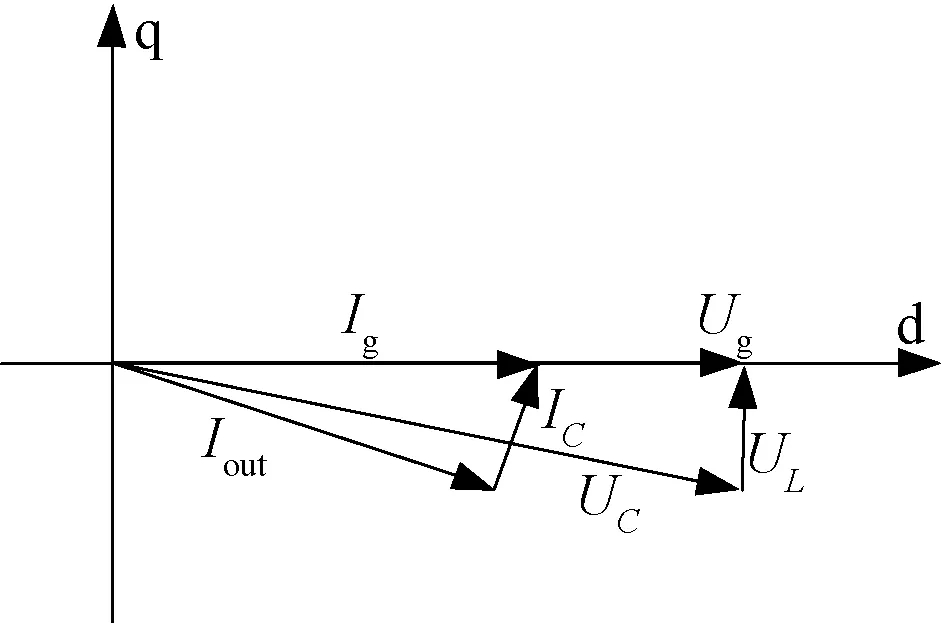
图6 加入功率因数控制后基于电网电压定向的ACCFig.6 Diagram of ACC based on grid voltage orientationafter adding power factor control

网侧单位功率因数运行时电容电压的相角θC满足：

(14)

式中，Im和Um分别为交流侧电网电流、电压的幅值。

本文提出的功率因数控制框图如图7所示，整个控制系统由两个控制环构成。直流电压控制环将采集到的直流电压Udc_measure与直流电压给定值Udc_ref比较，通过PI控制器调节得到触发角初始值，从而直接控制直流电压Udc的大小。在功率因数控制环中将网侧电网电流Ig在同步旋转坐标系下的q轴分量Igq作为一个反馈量与给定值Igq_ref(通常设为0)比较，通过PI控制器调节得到功率因数补偿角β。将ACC1的触发角设定为初始触发角α，且采用滞后于过零点触发，将ACC2的触发角设定为初始触发角加上功率补偿角之后得到的补偿触发角，且采用超前于过零点触发。

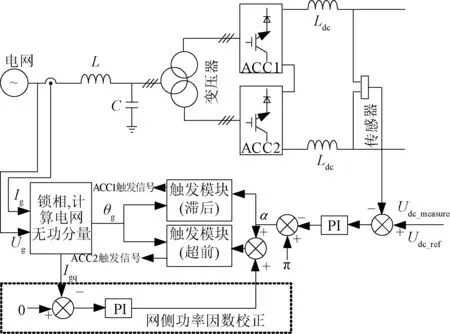
图7 引入功率因数控制后组合型基频开关ACC控制框图Fig.7 Control block diagram of combined ACC after introducing power factor control

引入功率因数补偿角β后，基于电网电压定相ACC1和ACC2的直流侧电压可以表示为：

(15)

由式(15)可以看出，基于电网电压锁相时ACC1、ACC2的直流侧电压引入功率因数补偿角后相较于采用功率因数控制前的不平衡度有所减轻，且能够实现网侧最大功率因数运行。

为了保证ACC1、ACC2传输的功率差值在一定可控范围内，需要对功率因数补偿角β的大小进行限制。即引入功率因数补偿角β后的ACC1、ACC2的直流侧电压需要满足：

(16)

式中，η为直流侧电压不平衡度。

3 仿真与实验验证

为了验证本文提出的直流侧电压控制及功率因数控制策略的正确性，在PSCAD/ETMC中搭建了基于组合型基频开关ACC的双端背靠背高压直流输电系统仿真模型，主电路参数见表3。

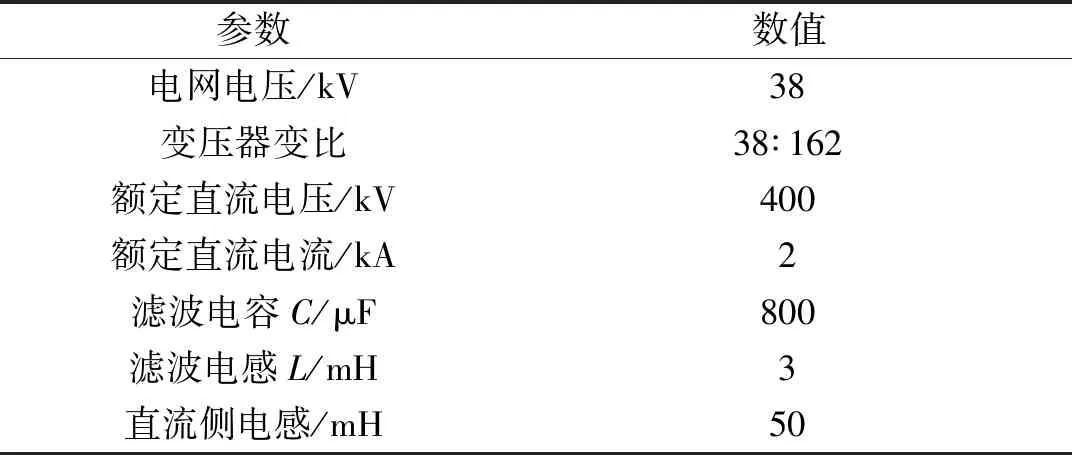
表3 ACC主电路参数Tab.3 Main circuit parameters of ACC

仿真模型中，受端组合型基频开关ACC控制直流输电系统直流电流，送端组合型基频开关ACC控制直流电压，20 s之前采用传统的直流侧电压控制，20 s时投入网侧功率因数控制，结果如图8所示。

组合型基频开关ACC直流侧电压如图8(a)所示，直流电压达到额定值，未加入网侧功率因数校正时，ACC1和ACC2的直流电压存在不平衡，投入网侧功率因数控制后，直流电压仍保持为额定值，ACC1、ACC2的直流电压不平衡度降低，ACC1、ACC2传输功率大致相等；图8(b)为受端交流侧电压、电流的dq轴分量，可以看出20 s加入网侧功率因数控制后，网侧电流的q轴分量降为0，基本实现网侧单位功率因数运行。图8(c)和图8(d)是组合型基频开关ACC交流侧电压、电流波形，可以看出，组合型基频开关ACC的a相输出电流Ia_ACC为五电平，未加入网侧功率因数控制时，组合型ACC输出电流Ia_ACC与交流侧电网a相电压Uga基本同相位，加入网侧功率因数控制后，Ia_ACC依然为五电平电流波形，Ia_ACC相位滞后于Uga，图8(e)和图8(f)分别为加入网侧功率因数控制前后网侧a相电流Iga与网侧a相电压Uga，加入网侧功率因数控制之前，网侧电流Iga相位超前于Uga，加入网侧功率因数控制之后Iga相位与Uga基本保持一致，实现网侧单位功率因数运行。额定工况下的网侧有功功率和无功功率如图8(g)所示，20 s之前未加入网侧功率因数控制，有功功率为800 MW，无功功率约为-375 MVar，加入网侧功率因数校正后，能够保持传输的有功功率一致，无功功率降到了0 Var，实现网侧单位功率因数运行。仿真结果与前面的理论分析一致。

为了验证本文所提出的基频开关调制策略和网侧功率因数控制方法的正确性，搭建了如图9所示的实验平台。

图9 ACC实验平台Fig.9 Experimental prototype of ACC

实验平台有控制保护机箱、两台ACC模块ACC1和ACC2、采样板、IO板、变压器及LC滤波电路组成，ACC模块桥臂选用的IGBT型号为ABB压接型器件ST1500GXH24，二极管为英飞凌的压接型器件D1600U45X122。实验平台电气参数见表4。

表4 实验参数Tab.4 Experimental parameters

实验中，组合型基频开关ACC作为整流器，控制直流侧电压，图10(a)、图10(b)为未加入网侧功率因数控制的实验波形，图10(c)、图10(d)为加入网侧功率因数控制的实验波形。从图10中可以看出，实验结果与仿真结果类似，ACC工作在基频开关状态，功率半导体器件的开关频率为50 Hz，ACC1的a相输出电流IACC1_a为三电平，未加入网侧功率因数控制时网侧交流线电压Uab与交流电流Iga和Igb的差值Iga-Igb存在相位差，Iga-Igb相位超前于Uab，直流侧电压Udc1与Udc2不平衡；投入网侧功率因数控制后，Iga-Igb与Uab相位基本一致，实现了单位功率因数运行，且直流侧电压Udc1与Udc2不平衡度降低。

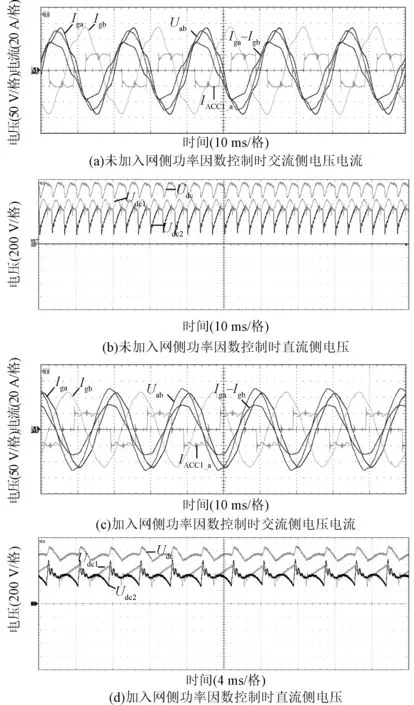
图10 实验波形Fig.10 Experimental waveforms

4 结论

本文针对由两台ACC直流侧串联、交流侧并联组成的组合型ACC，提出一种开关频率为50 Hz的基频开关高功率因数运行方法，并在此基础上，分析了基于电网电压定向时ACC的功率传输特性，为了进一步提高网侧功率因数，引入功率因数补偿角对基频开关ACC的触发角进行调整，使组合型基频开关ACC运行在网侧单位功率因数附近。仿真和实验结果均验证了本文理论分析及所提出的功率因数控制方法的正确性和有效性。