两种土壤墒情预报模型在沧州地区的应用及评价

韩红亮， 王雪梅

（杨凌职业技术学院，陕西 杨凌 712100）

“节水优先” 是新时代治水方针的重要内容，我国农业用水量占总用水量的60%以上， 因此做好农业节水对促进全国节水工作具有重要意义，通过做墒情预报提前预测土壤含水量， 进而采取精准、 及时的灌溉措施是促进农业节水的有效措施，所谓墒情，即土壤含水率。 土壤墒情预报的研究已有200 多年的历史，取得了一系列的成果。 发展至今， 墒情预报的主要方法有确定性模型和随机性模型，确定性模型主要包括水量平衡模型、土壤水动力学模型、SPAC 水热耦合传输模型等，随机性模型主要包括数理统计模型、 随机水量随机模型随机土壤水动力学模型等[1]。 1802 年道尔顿（Doulton） 提出了道尔顿蒸发蒸腾量计算公式，说明了影响作物腾发量的影响因素包括气象因素、土壤因素和作物因素。 1948 年彭曼（Penman）提出了Penman 公式，为计算参考作物腾发量提供了计算模型。1963 年蒙特斯（Monteith）在研究作物蒸发蒸腾时引入表面阻力的概念， 导出了Penman-Monteith 公式。 Jackson 等[2]基于植冠温度的研究，提出了作物水分胁迫指数（CWSI）的概念，该指数的提出， 证明了缺水指数与土壤含水量有较好的关系；1985 年Hargreaves 和Samain 共同提出了Hargreaves 模型[3]，尚松浩将Hargreaves 公式进行了修正，并提出了Hargreaves 的通用模型。 康绍忠[4-5]将土壤水分的模拟分为趋势项、周期项和时间项，提出了时间序列模型。Danior[6]研究了在土壤多样性和腾发量不确定性条件下， 土壤墒情的时间和空间方面的预报。 黄冠华等[7]利用彭曼公式，将作物系数拟合成随时间变化的函数， 来预测土壤含水率，精度在95%以上；茆智[8]提出了预测腾发量的指数模型， 该模型用多年气象数据来预测今后的参考作物腾发量，当代一些学者仍在使用[9-10]。尚松浩等[11]采用土壤水分消退指数曲线建立了土壤墒情预报的经验模型。 以上模型在墒情预报工作中有着较为广泛的应用， 取得了较好的实践效

果[12-13]。

但不同的预测方法在精度上存在着差别，甚至有的预测方法本身就存在着地域性的限制。 为帮助基层遴选较为简便操作的墒情预报模型，本文以沧州地区的土壤墒情的变化规律为研究对象，对比了2 种土壤墒情预报方法，在一定程度上可以为北方地区土壤墒情预报提供理论依据，对该地区的节水灌溉具有一定的现实意义。

1 材料与方法

1.1 试验区概况

试验区位于河北省南皮县冯家口镇， 距沧州市约40km 处[14]，地处北纬38°06′，东经116°40′。试验区为典型环渤海缺水盐渍化类型区， 土壤多为脱盐潮土，有部分盐化潮土和滨海盐土，耕地土壤为轻质壤土，土壤田间持水量32%（体积含水率），土壤干容重1.49g/cm3。 海拔在8m 左右，年降水量400—550mm。

南皮生态农业试验站内36 个实验小畦 （测坑），均为2.2m×3.0m 无底测坑。 共A、B 、C、D 等4个系列，每系列9 个测坑。其中A 系列和C 系列安装了遮雨棚，36 个小畦中均种植棉花。由于实验时部分测坑被占用， 且有2 个测坑试验期间不慎进水，故本文选取A1—A5，A8 共6 个连续测坑开展试验。

该试验站装有自动气象监测系统， 监测内容包括日照、 风速、 气温、 湿度等； 土壤墒情采用Dviner 快速测量系统监测，由工作人员每日监测土壤含水率； 试验站工作人员进行每天的天气状况记录。 本文研究的数据均来自试验站1954—2016年的气象数据、2018 年天气记录， 以及2018 年墒情监测站测得的数据。

本文开展的墒情预报， 是对逐日土壤含水率的预报。

1.2 研究方法

1.2.1 用ET0 指数模型预测土壤墒情

指数模型是利用沧州地区多年的气象数据来预测今后的该地区参考作物腾发量， 通过计算作物的蒸发量，来预测土壤逐日的含水率。

参考作物腾发量计算采用FAO 推荐的彭曼公式：

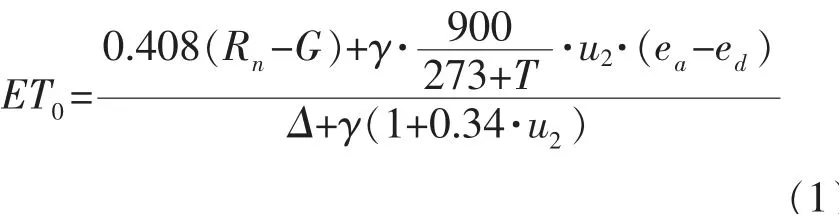
式中：ET0为参考作物蒸发蒸腾量，mm/d；

Δ 为温度-饱和水汽压关系曲线上在T处的切线斜率，kpa/℃；T为平均气温，℃；ea为饱和水汽压，kPa；ed为 实 际 水 汽 压，kPa；Rn为 净 辐 射，MJ/m2·d；G为土壤热通量，MJ/m2·d；u2为2m 高处的风速，m/s；γ 为温度表常数，kPa/℃（可由高程和温度计算得出）。

茆智于1995 年提出的ET0的指数模型：

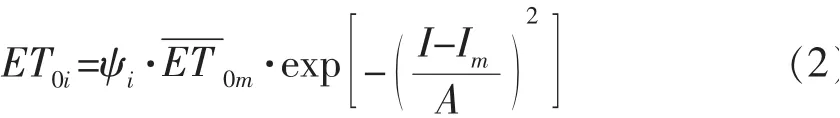
式中：ET0m为多年平均最大旬参考作物腾发量平均值，mm/d；I为日序数（元月1 日为1）；Im为历年中出现之日的序数；A为经验参数， 华北平原取112；ψi第i天天气类型的修正系数。

作物实际腾发量的计算公式：

式中：ET0为参考作物蒸发蒸腾量，mm /d；KC为作物系数；KS为土壤水分修正系数，按（4）计算。

式中：θi第i日实际土壤含水率， 以占田间持水量的百分数计，%；θc土壤水分胁迫临界含水率，旱作物为占田间持水量的60%；ε 经验系数， 旱作物为0.89。

1.2.2 用消退指数法预测土壤墒情

在有水分胁迫的条件下， 蒸腾量与土壤含水率之间近似直线关系：式中：W为根系层贮水量，mm；t为时间，d；k为土壤水分消退指数。

在不考虑降水及灌溉的条件下：

式中：Wt，Wt+1分别为第t天和第t+1 天的土壤根系层贮水量，mm。

由前期的水分资料，使用式（5）、（6）来拟合消退指数的发展变化规律曲线，再用式（7）来反推其后的消退变化：

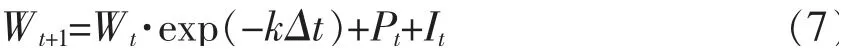
2 墒情预报的分析和比较

2.1 用ET0 指数模型法预测土壤墒情

我国泊头气象站距离试验区15km， 两地的气象资料具有一致性。 借用沧州泊头站1954—2016年的气象资料，通过式（1）计算逐日的参考作物腾发量， 计算每年的参考作物腾发量最大旬的平参考作物腾发量，求其均值即式（2）的ET0m，每年发生的ET0m日序数（每年的1 月1 日的日序数为1，依次类推）， 多年发生ET0m日序数的平均值即Im。即可求得式（2）的各个参数。 然后式（3）计算逐日腾发量。

经计算， 该地区多年平均最大旬参考作物腾发量平均值为7.42mm/d， 对应的历年中出现ET0m之日的序数为163，发生在6 月上旬，则计算得到该地区ET0i的计算式为

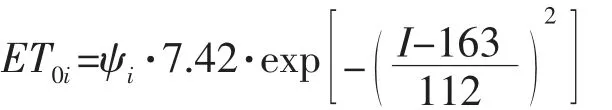
根据2018 年的天气记录，查的天气类型修正系数见表1。

2018 年5 月28 日到6 月16 日棉花处于苗期生长阶段， 此阶段内棉花的作物系数为0.731，此阶段的土壤系数由式（4）根据当日的根系层平均含水率逐日计算。 试验站土壤的田间持水量为32%（体积含水率），故

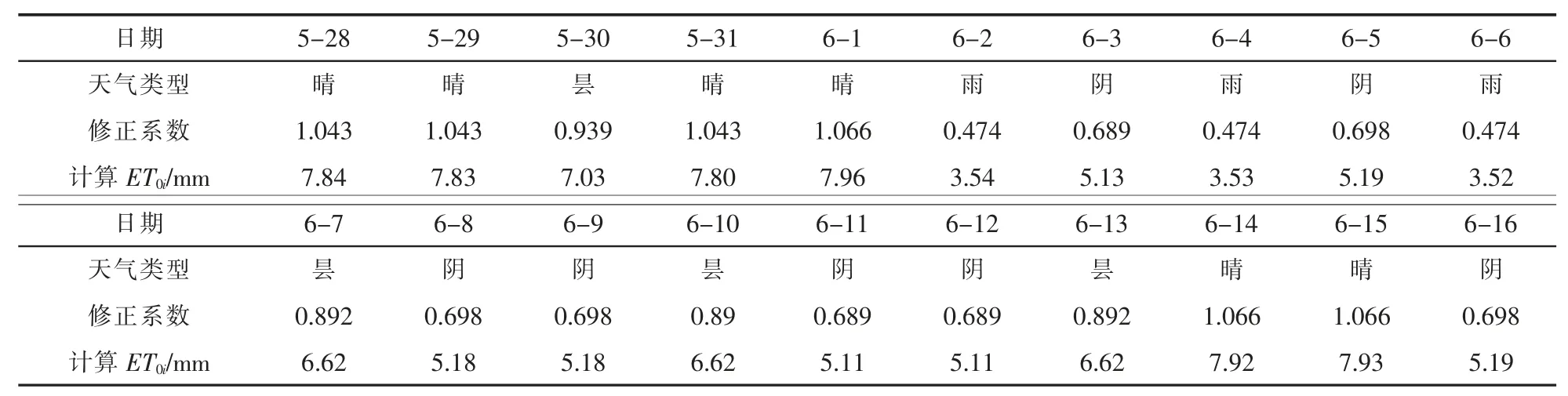
表12018 年试验站天气情况及修正系数

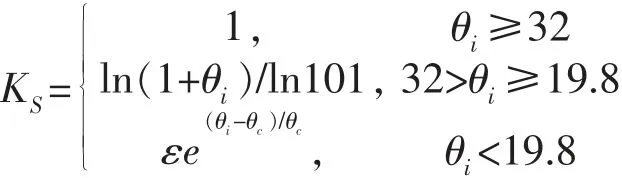
式中：θi为土壤体积含水率，%。

以2018 年5 月28 日为起始日期， 逐日预测各畦的土壤含水率，并与6 月8 日，6 月16 日各畦的实测墒情进行比较。 由于该期间A6、A7、A9 畦下雨时不慎进水， 故不再对这三个畦的墒情做预报。 预测各畦6 月8 日和6 月16 日的土壤含水率见表2。

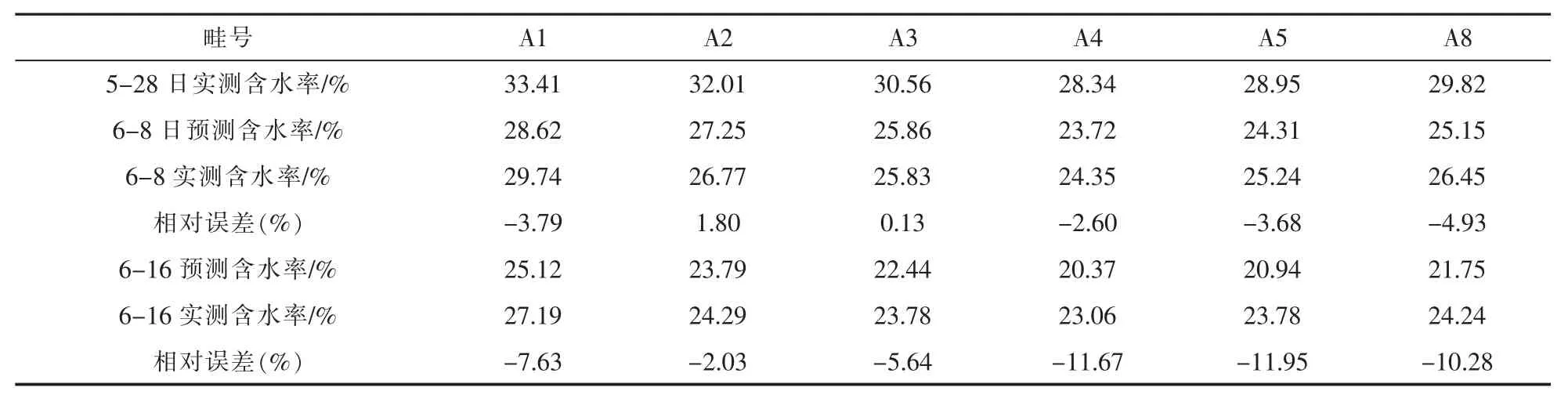
表2 指数模型法预测结果

2.2 用消退指数模型预测土壤墒情

根据A1—A8（除A6、A7、A9外）各畦的4 月22日—5 月28 日（此阶段各测畦均未灌水）日的作物根系层的贮水量（水层深度），计算逐日的消退指数值，将消退指数的变化拟合成与时间的函数，然后根据此函数的变化趋势， 计算未来的消退指数值，最后使用式（7）计算未来某天的贮水量，并计算土壤的平均含水率（期间无灌水，故P=0，I=0）。

拟合的A系列的6 个小畦消退指数曲线，如表3。

表3 消退指数拟合曲线

根据拟合成的消退指数函数，由式（7）计算6月8 日和6 月16 日的土壤贮水量和土壤含水率，计算结果见表4。

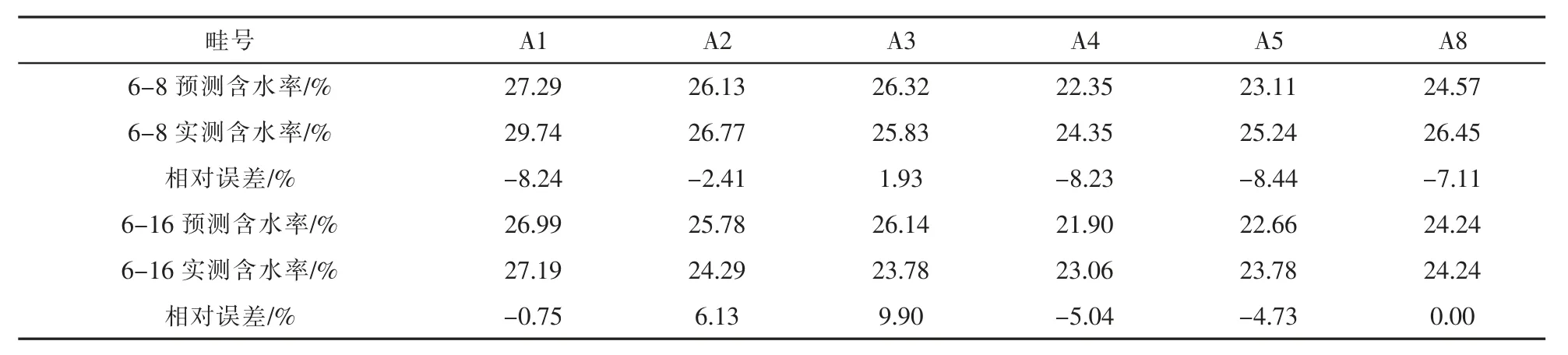
表4 消退指数法预测结果

2.3 比较分析

（1） 分别将两种预报方法的预测值与实测值比较，采用t检验方法将墒情的预测值与实测值进行比较，进而反映两种模型的预测精度。 经比较，发现这两种方法对6 月8 日墒情的预测， 均无显著性差异， 对6 月16 日的预测， 误差均值有显著性差异，分析结果见表5。

表5 两种方法预测精度比较表

（2）用最小二乘法分析两种方法的预报误差，即对各畦预测误差的平方和进行比较，结果表明，对6 月16 日墒情的预测，前者的误差平方和大于后者误差平方和， 可见指数模型法在预测初期效果较好，预测后期误差比消退指数法要大，计算结果见表6。

表6 预测方案误差平方和

3 结论

（1）经过t检验分析，两种预测方法的预测值与相应的实测值均无显著性差异， 证明两种方法均适用于沧州地区的墒情预报。

（2）通过对两种方法预报精度的t检验，表明在预测较长时间的墒情时， 消退指数法的预报精度要高于指数模型法。

4 有待研究的问题

指数模型预测墒情的基本原理， 是通过计算逐日作物腾发量来预测含水率， 因为每天的预测值都可能有一定的误差， 所以， 当预测时段较长时，该模型的误差可能会逐渐增大，如何解决这个问题，有待继续研究。 □