全因子试验设计的土坝变形参数全局敏感性分析

孙一清,杜一峰,杨庆庆,王桂智,甘 磊,周东昊,陈官运,冯先伟

(1.河海大学 水利水电学院，江苏 南京 210098;2.上海市松江区水务管理所，上海 201699;3.扬州市勘测设计研究院有限公司，江苏 扬州 225007;4.江苏省水利勘测设计研究院有限公司，江苏 扬州 225127)

1 研究背景

大坝是重要的水利工程建筑物，由于存在各种外部和内部载荷，必然会产生相应的变形，大坝变形达到临界极限时，可能会发生严重破坏甚至完全坍塌[1]，所以有必要对大坝变形进行实时监测及数值模拟研究。在众多坝型中，土坝是世界上最古老的坝型之一[2]，其中均质土坝最为经济实用，因此关于均质土坝的变形研究较多[1,3-6]。其中，Guo等[6]将克里金替代模型、蒙特卡洛模拟、sobol敏感性分析法与一阶可靠性方法相结合，调查了输入变量在土坝稳定性研究中的重要性；Dong等[4]以中国某高土石坝为例，采用邓肯-张E-B模型进行静力分析，并通过与监测数据对比发现该模型能够较好地描述土石坝的变形。可见，对于土坝的研究已经不再局限于有限元分析，越来越多的学者开始就方法和本构模型对土坝的稳定性进行研究。

在土石坝变形计算较为常用的本构模型中[7]，弹塑性模型的参数很难获得，计算过程也非常复杂。在非线性弹性模型中，邓肯-张模型(Duncan-Chang E-v模型或Duncan-Chang E-B模型)常被用于分析大坝的结构性态[8]，其中，邓肯-张E-B模型中每个参数均具有清晰的物理和几何意义，不仅可以通过常规三轴剪切试验简单地获得[9]，还可以通过智能算法进行反分析。但该模型参数的反演需要建立参数与变形结果之间的目标函数，最后转化为多目标优化问题[10]，并且需要大量的模拟数据作为支撑，因而研究者们逐渐开始采用敏感性分析方法对模型参数进行研究。在考虑输入参数的不确定性对模型响应输出的影响程度时，通过敏感性分析可以给出系统中各参数的重要程度[6]，即可忽略对结果影响不显著的参数，仅考虑对结果影响显著的重要参数，从而提高研究效率[11]。早期更多地采用单因素进行敏感性分析，该方法属于局部敏感性分析的一种[12]，现有的局部敏感性分析方法主要包括有限差分敏感性分析法、场景分解和广义龙卷风图、蜘蛛图和单向灵敏度函数以及基于微分的方法等[13]。但上述方法在不同程度上具有线性、正态性和局部变化的局限性[14]。事实上，广义的敏感性分析方法还包括全局敏感性分析方法，与局部敏感性分析相比，全局敏感性分析不仅可以反映出每个因素的影响，还可以反映所有因素相互作用的影响[15]。全局敏感性分析方法可以分为基于回归的方法、基于试验设计和筛选设计的方法、基于方差的方法和基于元模型的方法等[16]。

近年来，敏感性分析越来越多地被应用于大坝工程研究中。Li等[17]利用基于方差的全局灵敏度分析方法，从3个不同的层面对大坝的静力性能进行了分析；Liang等[18]采用具有近似矩估计的拉丁超立方体抽样(Latin hypercube sampling，LHS)方法研究高拱坝地震稳定性能的参数敏感性；Chen等[19]用修正的莫里斯法初步分析了耦合E-v和修正Burgers模型中参数的灵敏度；Yao等[10]用响应面法代替人工神经网络，描述了E-B模型参数与大坝沉降之间的敏感性关系；Ren等[20]以陕西省某土石坝为例，采用Morris方法研究了热液耦合模型参数对土石坝温度场的敏感性；Lakehal等[21]以均质土边坡为例，采用中心组合设计试验方法，研究了E-B模型参数与安全系数之间的敏感性。与上述敏感性分析方法一样，全因子试验设计同样属于试验设计和筛选设计方法中的一种[22]，其虽然需要较多的试验次数，但优点是可以得到准确可靠的结果，并计算出所有因素的主效应和交互效应，主效应即一个因素各水平变化造成结果变化的程度，且该变化程度不受其他因素各水平变化的影响，交互效应即一个因素各水平变化造成结果变化的程度，且该变化程度受其他因素各水平变化的影响。Golshani等[23]以尾矿坝中的煤精矿为研究对象，采用全因子设计分析酸碱度、粒度等因素对于煤精矿硫还原的敏感性影响；Kadeethum等[24]采用全因子试验设计，针对多孔介质裂缝中流体力学对于油井产能的影响进行了统计敏感性分析。

目前，全因子试验设计鲜有被用于水工程领域的案例，且多数水工程中的敏感性分析方法未考虑因素间的交互效应，因而缺少对因素的全局敏感性分析。本文以甘肃省某黄土均质坝为研究对象，通过有限元法分析程序构建反映土石坝结构的静力分析模型，求解大坝位移变化，再借助Plackett-Burman试验设计对均质土坝变形参数进行显著性筛选，并利用全因子试验设计对影响均质土坝变形的显著参数进行全局敏感性分析，最后建立了相应的回归模型，以期为黄土均质坝变形模拟计算参数的选取提供参考。

2 敏感性分析方法

以黄土坝壳全计算区域为研究对象，采用全局敏感性分析方法研究坝料密度和邓肯-张E-B模型参数对黄土均质坝的敏感性。在全局敏感性分析中，由于全因子试验设计只能考虑至多5个因素的敏感性以及因素间的交互效应，所以有必要先对考察因素进行科学合理地显著性筛选，而Plackett-Burman试验设计可以实现这一过程，经筛选后再进行全因子试验，以得到全局敏感性分析结果。全局敏感性分析方法具体过程如下：

(1)Plackett-Burman试验设计。利用Plackett-Burman试验设计对8个计算参数进行试验设计，运用方差分析法分析结果，筛选掉其中不显著的参数，保留显著的参数。

(2)全因子试验设计。对通过Plackett-Burman试验设计保留下来的参数进行全因子试验设计，对这些参数进行主效应分析和交互效应分析，绘制出等值线图及响应曲面图，最后使用方差分析，寻找敏感性较强的几个参数及其组合。

方差分析借助统计量F值来判定显著性，其计算方法如下：

(1)

式中：MSi为各因素的均方；MSe为误差的均方。

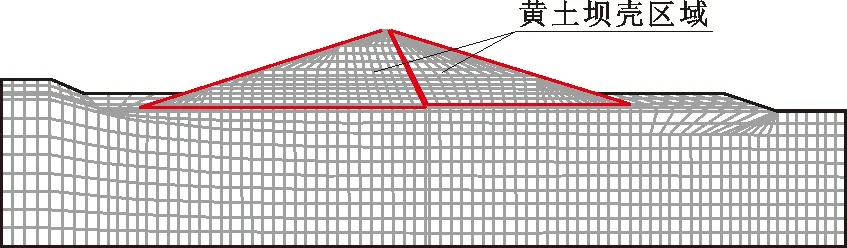
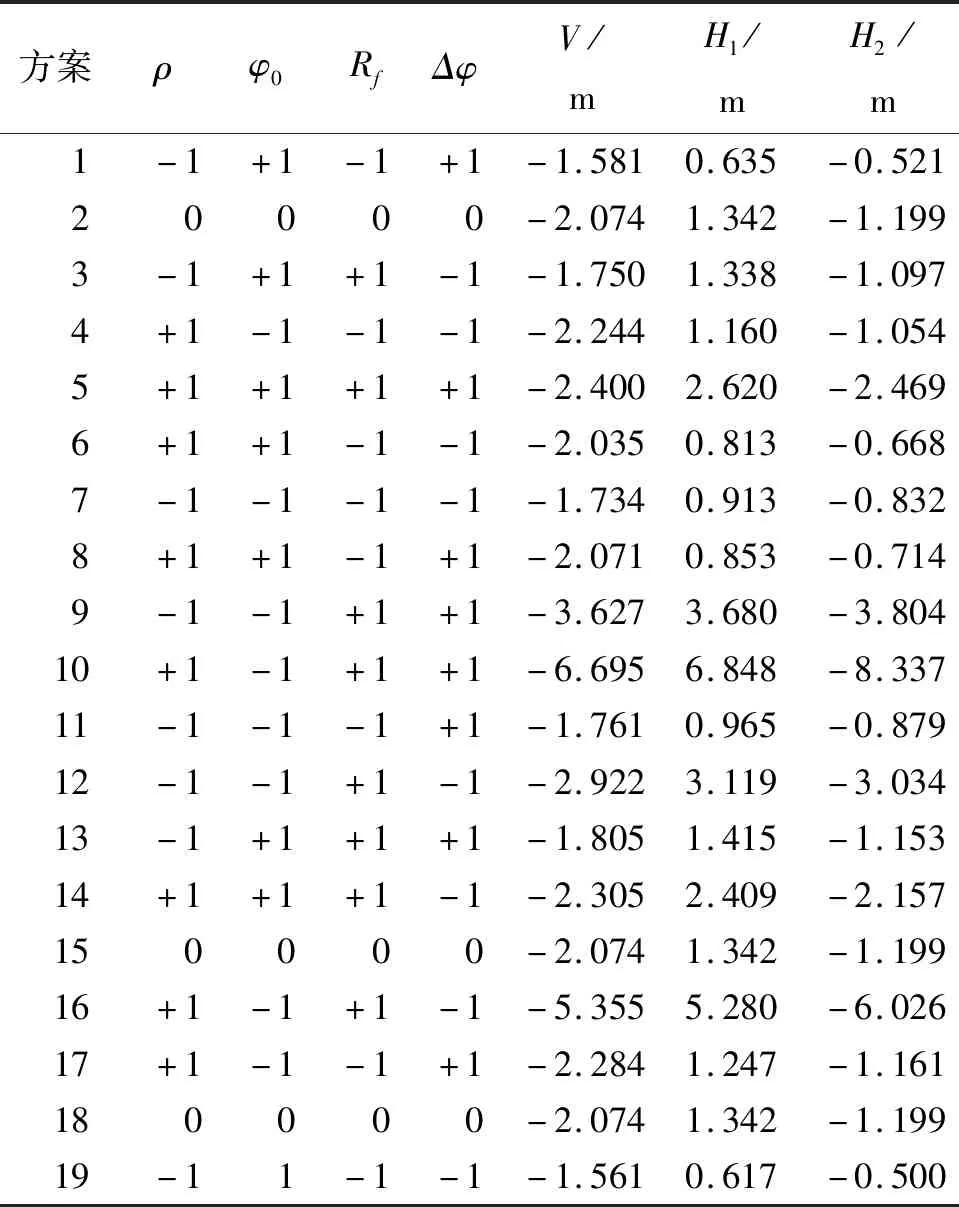
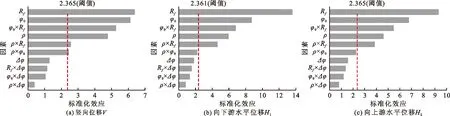
若Fi>F0.01，说明该因素影响明显显著，记为“**”；若F0.01>Fi>F0.05，说明该因素影响显著，记为“*”；若F0.05>Fi>F0.1，说明该因素有影响，记为“☉”；若F0.1>Fi>F0.2，说明该因素有一定影响，记为“△”；若Fi

邓肯-张E-B模型共有10个参数，分别为黏聚力C、初始内摩擦角φ0、摩擦角Δφ、破坏比Rf、初始弹性模量基数K、初始体积模量基数Kb、初始弹性模量指数n、初始体积模量指数m、卸荷再加荷时的弹性模量基数Kur、卸荷再加荷时的弹性模量指数nur。在参数选择时，由于黄土土坝施工填筑过程中，坝壳室中处在荷载状态，且黄土颗粒为散粒体材料，故参数C、Kur和nur不参与讨论，同时施工过程中坝料密度ρ也是一个影响黄土坝壳变形的因素，因此选择ρ、φ0、Δφ、Rf、K、Kb、n、m这8个参数进行敏感性分析。

2.1 Plackett-Burman试验设计

Plackett-Burman试验设计被广泛应用于实际工作中，其主要作用是筛选试验因素。分别对多个影响试验指标强弱程度不详的试验因素取高(+1)低(-1)两个水平，借助试验设计表格研究试验因素多个水平间变化对于试验指标的影响，筛选出对试验指标影响显著的试验因素，以便减少后续研究的工作量。Plackett-Burman试验设计按规则生成，排列可具有不唯一性，实际研究中需保留3个以上虚拟变量，即对于M次试验，所研究因子应小于等于M-4个。且试验次数M应为4的倍数，但不包括2的幂次方。常用的取值为M=12、20、24、28、36等。

2.2 全因子试验设计

全因子试验设计不仅可以分析考察因素对于试验指标的敏感性，得到敏感性排序，还可以有效地估计出所有因素的主效应和各阶交互效应，生成交互效应较强组合的等值线图和响应曲面图，并对结果进行方差分析。全因子试验设计要求对所考察的全部因素的全部水平至少进行一次试验，其分析结果真实可靠。在需要考虑因素之间交互效应以获得较精确的分析结论时，常选择全因子设计。全因子试验设计通常不超过5个因素且水平为2。

3 工程实例

某水库大坝工程为黄土均质坝，最大坝高为125.00 m，坝顶高程为1 653.00 m。正常蓄水位为1 650.00 m，总库容为1.40×108m3。形成的有限单元网格共有11 324个结点和10 877个单元。黄土均质坝模型范围及有限元网格划分见图1，坝体各料区的计算参数取值如表1所示，分级加载及蓄水过程如表2所示。大坝运行期坝体典型断面的位移分布如图2。整体来看，该坝的变形分布符合一般均质土坝的分布规律，竣工期坝体水平位移以坝轴线为中线对称分布，运行期坝体水平位移在水压力的作用下稍有偏移；竖向位移呈现均匀下降趋势，位移最大值在坝体高度的2/3处，且运行期最大值大于竣工期最大值。

图2 实例工程运行期坝体典型断面位移分布(单位：mm)

表1 实例工程坝体有限元静力计算参数

表2 实例工程有限元计算分级加载及蓄水过程

图1 实例工程黄土坝模型范围及有限元网格划分

4 敏感性分析

4.1 Plackett-Burman试验

对ρ、φ0、Δφ、Rf、K、Kb、n、m这8个参数进行Plackett-Burman试验设计，每个参数考察两个水平，高水平(+1)取试验设计参数的1.2倍，低水平(-1)取试验设计参数的0.8倍，如表3所示。具体试验方案和试验结果(竖向位移V、向下游水平位移H1和向上游水平位移H2)如表4所示，分析结果如表5所示。

表3 Plackett-Burman试验各因素水平

表4 Plackett-Burman试验方案及各方案试验结果

由表5中试验分析结果可以看出，通过Plackett-Burman试验设计对8个变形计算参数进行筛选，各参数关于竖向位移V的敏感性排序为Rf>φ0>ρ>Δφ>n>Kb>m>K，其中对于竖向位移影响明显显著的参数为Rf、φ0和ρ，影响显著的因素为Δφ；各参数关于向下游水平位移H1的敏感性排序为Rf>φ0>ρ>Δφ>n>m>K>Kb，其中对于向下游水平位移影响明显显著的参数为Rf和φ0，影响显著的参数为ρ和Δφ；各参数关于向上游水平位移H2的敏感性排序为Rf>φ0>Δφ>ρ>n>Kb>m>K，其中对于向上游水平位移影响明显显著的参数为Rf和φ0，影响显著的参数为ρ和Δφ。

表5 各参数关于坝体不同方向位移的试验敏感性分析结果

综合来看，Rf、φ0、ρ和Δφ这4个参数对于黄土均质坝变形的影响更加显著，因而在计算参数中需要重点考虑，而n、Kb、m和K这4个参数可以视为对大坝变形无影响。

4.2 全因子试验

对上述Plackett-Burman试验设计筛选出的对黄土均质坝变形影响显著的参数Rf、φ0、ρ和Δφ进行全因子试验设计，研究该4个参数两两之间的交互效应。每个参数考察两个水平，高水平(+1)取试验设计参数的1.2倍，低水平(-1)取试验设计参数的0.8倍。具体试验方案及结果如表6所示。

表6 全因子试验方案

4个参数对大坝各方向变形的主效应如图3所示。由图3(a)和3 (c)可知，造成竖向位移和向上游水平位移变化差异明显的参数为ρ、φ0和Rf，且随着ρ和Rf的增大，竖向位移和向上游水平位移的数值显著减小，随着φ0的增大，竖向位移和向上游水平位移的数值显著增大；而无论其他3个参数如何改变，造成竖向位移和向上游水平位移的数值变化差异不明显的参数为Δφ。由图3(b)可知，造成向下游水平位移的数值变化差异明显的参数为ρ、φ0和Rf，且随着ρ和Rf的增大，向下游水平位移的数值显著增大，随着φ0的增大，向下游水平位移的数值显著减小，而无论其他3个参数如何改变，造成向下游水平位移的数值变化差异不明显的参数为Δφ[25]。

图3 4个参数对大坝各方向变形的主效应图

4个参数两两交互对大坝变形的效应如图4所示。由图4可以看出，对于竖向位移、向下游水平位移和向上游水平位移来说，仅有ρ×Rf和φ0×Rf两组交互效应的效应线相对角度明显较大，说明ρ×Rf和φ0×Rf的交互效应显著[26]，即一个因素各水平变化造成结果的差异会受另一因素各水平变化的影响，而ρ×φ0、ρ×Δφ、φ0×Δφ、Rf×Δφ4组交互效应的效应线相对角度较小，说明交互效应不显著。

图4 4个参数两两交互对大坝变形的效应图

由交互效应分析可知，ρ×Rf和φ0×Rf两组效应需要重点关注。设定另外两个变量在最佳参数时，绘制两组效应下大坝竖向位移、向下游水平位移和向上游水平位移的等值线，如图5所示。由图5可看出，在保持φ0为26°和Δφ为5°不变时，随着ρ和Rf的增大，竖向位移和向上游水平位移的数值逐渐减小(位移量增大)，而向下游水平位移的数值逐渐增大(位移量增大)；保持ρ为17 g/cm3和Δφ为5°不变，随着φ0的减小和Rf的增大，竖向位移和向上游水平位移的数值逐渐减小(位移量增大)，而向下游水平位移的数值逐渐增大(位移量增大)。再对ρ×Rf和φ0×Rf两组交互效应下绘制竖向位移、向下游水平位移和向上游水平位移相应的响应曲面图，如图6所示。由图6可见，对于3个方向的位移而言，ρ和Rf越大，则位移越大，当ρ为20.4 g/cm3、Rf为0.9时，位移达到最大值；φ0越小、Rf越大，则位移越大，当φ0为20.8°、Rf为0.9时，位移到达最大值。

图5 ρ×Rf和φ0×Rf两组交互效应下大坝各方向位移等值线 图6 ρ×Rf和φ0×Rf两组交互效应下大坝各方向位移响应曲面

方差分析结果见表7，表7中方差分析结果为不同参数及其组合的敏感性统计量Fi值，Fi值越大则敏感性越强。由于Plackett-Burman试验筛选出的显著参数Rf、φ0、ρ和Δφ相互之间的三阶及四阶交互效应显著性太小，在此不予分析。

表7 4个参数及其交互效应敏感性的方差分析结果

由表7可知，对于竖向位移，Rf、φ0、ρ和Δφ4个参数及其交互效应的敏感性排序为Rf>φ0>φ0×Rf>ρ>ρ×Rf>ρ×φ0>Δφ>Rf×Δφ>φ0×Δφ>ρ×Δφ，其中，Rf、φ0、φ0×Rf和ρ的影响明显显著，ρ×Rf和ρ×φ0的影响显著；对于向下游水平位移，Rf、φ0、ρ和Δφ4个参数及其交互效应的敏感性排序为Rf>φ0>φ0×Rf>ρ>ρ×Rf>ρ×φ0>Δφ>Rf×Δφ>φ0×Δφ>ρ×φ0。其中，Rf、φ0、φ0×Rf和ρ×Rf的影响明显显著，ρ×φ0有影响；对于向上游水平位移，Rf、φ0、ρ和Δφ4个参数及其交互效应的敏感性排序为Rf>φ0>φ0×Rf>ρ>ρ×Rf>ρ×φ0>Δφ>Rf×Δφ>φ0×Δφ>ρ×φ0。其中，Rf、φ0、φ0×Rf和ρ×Rf的影响明显显著，ρ×φ0有影响。

通过方差分析得到4个参数及其交互效应的敏感性排序为Rf>φ0>φ0×Rf>ρ>ρ×Rf>ρ×φ0>Δφ，与前文Plackett-Burman试验分析得到的敏感性排序Rf>φ0>ρ>Δφ相符合。而φ0×Rf和ρ×Rf的敏感性是需要重点关注的。

将方差分析结果绘制成大坝变形标准化效应的Pareto图，如图7所示。由Pareto图可以更加直观地观察判断出各因素的显著性。其判断方法是：如果某因素对应的矩形条超过标准化效应阈值，则该因素为显著影响因素[25]。

图7 大坝变形标准化效应的Pareto图

由图7可知，Rf、φ0、ρ3个参数的主效应显著，φ0×Rf、ρ×Rf的二阶交互效应显著，Δφ及其余二阶效应均不显著，与前文中主效应及交互效应分析结果一直。将Δφ及其余二阶项剔除，对大坝变形标准化效应的Pareto图中显著的因素建立回归模型。

竖向位移的回归模型为：

V=7.89+0.269ρ-0.441φ0-15.05Rf-

0.570ρ·Rf+0.766φ0·Rf

(2)

向下游水平位移的回归模型为：

H1=-7.61+0.455ρ+0.437φ0+14.62Rf-

0.817ρ·Rf+0.784φ0·Rf

(3)

向上游水平位移的回归模型为：

H2=8.94+0.633ρ-0.579φ0-16.91Rf-

1.107ρ·Rf+1.026φ0·Rf

(4)

对于竖向位移回归模型，R2=0.8905，R2(预测)=0.7198，R2(调整)=0.8358；对于向下游水平位移回归模型，R2=0.9493，R2(预测)=0.8702，R2(调整)= 0.9239；对于向上游水平位移回归模型，R2=0.9171，R2(预测)= 0.7877，R2(调整)= 0.8756，表明各方向位移的回归模型的拟合性较优。

综合来看，Rf、φ0、φ0×Rf、ρ、ρ×Rf对黄土均质坝变形敏感性更强，可以在考虑交互效应的正交试验中重点考察。

5 结 论

为了全面探究大坝变形参数对于均质土坝变形的影响，本文选取甘肃省某黄土均质土坝作为案例，通过有限元分析程序建立了均质土坝静力分析模型，分析了该坝在竣工期和运行期的位移变化规律；使用Plackett-Burman试验设计对邓肯-张E-B模型参数及坝料密度进行对于大坝变形的显著性筛选；对筛选出的显著参数进行全因子试验设计，研究对于均质土坝变形影响显著的参数及其组合，得到以下主要结论：

(1)该土坝的变形分布符合一般均质土坝的分布特点，竣工期坝体水平位移呈对称分布，运行期坝体水平位移在水压力的作用下由对称分布逐渐向下游变形。竖向位移呈现均匀下降趋势，最大值在坝体高度的2/3处。

(2)对于Plackett-Burman试验设计中的ρ、φ0、Δφ、Rf、K、Kb、n、m这8 个参数，需要重点考虑的是Rf、φ0、ρ和Δφ，而n、Kb、m和K4个参数可以视为对大坝变形无影响。

(3)在全因子试验设计中分别进行了主效应分析、交互效应分析、方差分析，并且对交互效应明显显著的参数组合进行等值线图和响应曲面图分析，并建立相应的回归模型。得到的结论是：被筛选出的4个参数中，Rf、φ0和ρ3个参数的主效应明显显著，且ρ和Rf、φ0和Rf两个参数的交互效应敏感性不能被忽视。