基于Kmeans-EMD与IWOA-Elman的碾压速度异常值检测与修正

乔天诚，佟大威，王佳俊，关 涛，吴斌平

(天津大学 水利工程仿真与安全国家重点实验室，天津 300072)

1 研究背景

目前，水利工程建设已逐步趋于智能化。由于在大坝建设过程中的压实质量实时评价可有效弥补事后评价的低时效性，极大提升工程质量的控制水平与效率，因而其评价方法得到了广泛研究[1-2]。筑坝碾压监控系统可实现对施工过程的有效控制，为压实质量评价奠定数据基础，因此该系统已普遍应用于大坝施工过程[3-5]。但碾压监控系统仅侧重对碾压速度的整体把控，即动态采集与调整，却未实现对碾压速度异常值的检测与修正，因而无法保障所采集的碾压速度数据的质量。

大坝填筑碾压速度是评价其压实质量的重要指标[6-7]，在监控过程中，碾压速度的本质是依托GPS(global positioning system)定位设备采集的连续时间序列，但GPS定位设备存在定位漂移、数传延迟等问题，且人为因素与仓面平整度也会导致数据异常。异常值不仅会影响碾压速度的数据质量，还易降低压实质量的评价精度，但当前尚缺乏相关分析方法，无法有效实现碾压速度的异常值检测与修正，故开展基于Kmeans-EMD与IWOA-Elman的碾压速度异常值检测与修正研究具有重要意义。

异常值是导致数据质量降低的重要因素，在各行业内均得到极大重视，其相关研究也取得了丰硕成果，如孤立森林算法[8]、移动小波树[9]、LOF指数法[10]、箱线图法[11]等均被成功应用于异常值检测。但由于碾压速度具有较强的时序变化特征，平稳性较差，其加速与减速阶段的交互影响不利于基于统计学方法的异常值检测，故本文通过Kmeans算法[12]与EMD(empirical mode decomposition)[13]从定性与定量两个角度检测碾压速度中的异常值，以保障异常值检测的精度。

尽管异常值检测是确保数据质量的基础，但异常值检测却会破坏原有的数据序列结构，因此异常值修正同样是确保数据质量的重要部分。异常值修正可确定异常位置下的合理取值，保障数据的完整性，提高数据可靠性[14]。碾压速度作为一维时间序列，其异常值修正通常需依托同序列的其他数据并结合预测模型实现，如支持向量机[15]、径向基神经网络[16]、极限学习机[17-18]、长短期记忆神经网络[19]、Elman神经网络[20]等均可用于异常值修正。而其中，Elman神经网络承接层的设定使其具有更高的敏感性和更强的动态信息记忆与处理能力[21]，故本文将基于Elman神经网络实现碾压速度的异常值修正，并利用鲸鱼优化算法(whale optimization algorithm，WOA)优化Elman神经网络的初始权值与阈值，同时针对WOA存在的不足进行改进，形成IWOA-Elman神经网络。

综上所述，本文将基于Kmeans算法、EMD、IWOA-Elman神经网络开展有关碾压速度异常值检测与修正的研究：首先，结合碾压速度的时序变化特征，利用Kmeans算法与EMD从定性与定量两个角度检测碾压速度中的异常值；进而，为保障碾压速度数据的完整性与可靠性，确保良好的数据序列结构，利用IWOA-Elman神经网络构建碾压速度异常值修正模型，从而提高碾压速度的数据质量，为压实质量高精度评价奠定良好的数据基础。

2 研究方法

本文结合Kmeans算法与EMD对碾压速度进行异常值检测，并利用IWOA-Elman神经网络构建碾压速度异常值修正模型，以提高碾压速度的数据质量，研究框架如图1所示，具体研究方法如下：

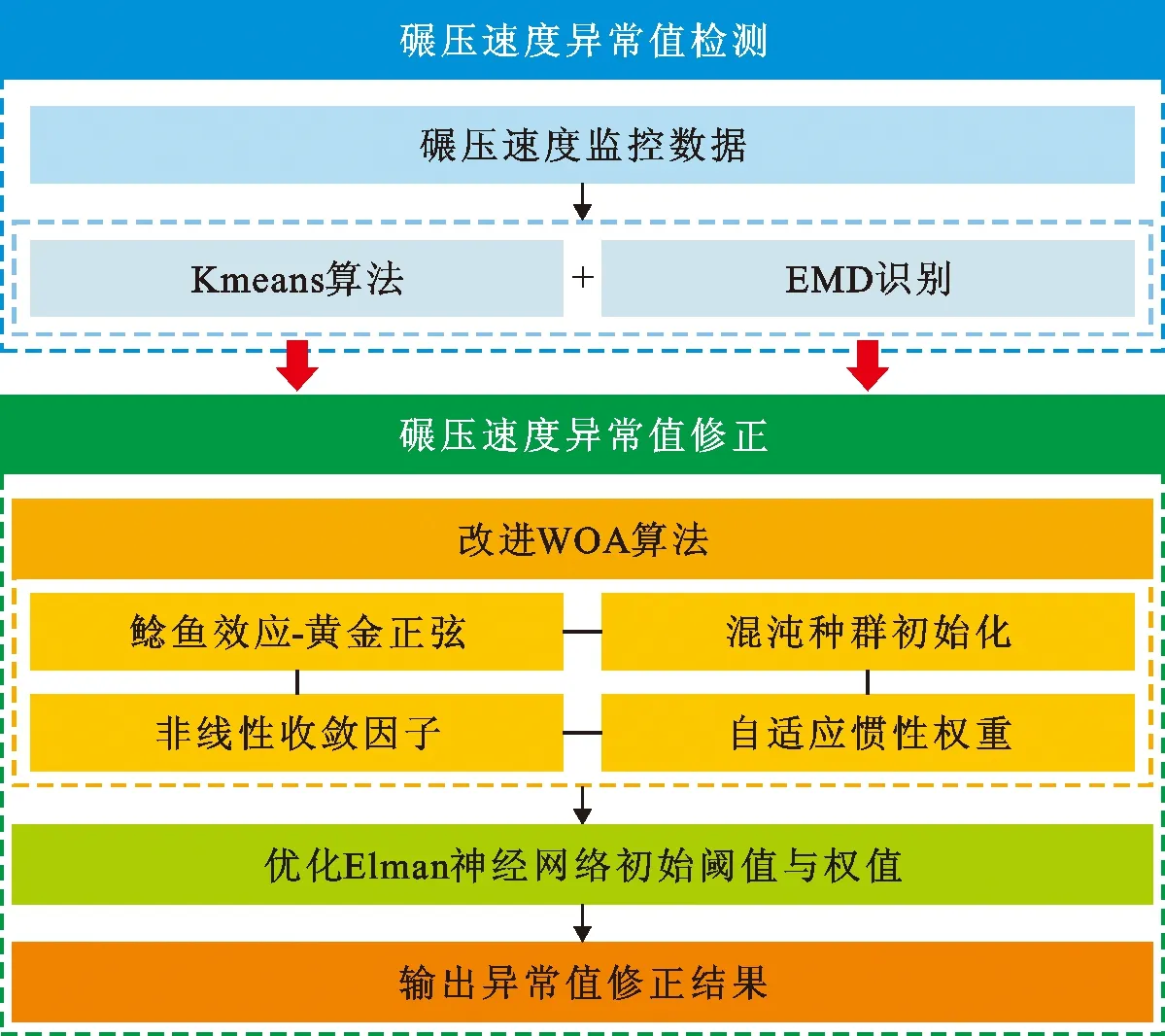
图1 筑坝碾压速度异常值检测与修正的研究框架

(1)本文研究基于西南地区某心墙堆石坝工程开展，考虑到心墙堆石坝心墙区压实质量对大坝整体建设质量有重要影响，故选择心墙区凸块碾压机速度监控数据为研究对象；

(2)本文通过以下4方面内容实现对碾压速度异常值的检测与修正：①结合碾压速度的时序变化特征，先后利用Kmeans算法与EMD对碾压速度中的异常值做初步定性与精细定量检测，保障异常值检测的精度；②利用混沌种群初始化、非线性收敛因子、自适应惯性权重与鲶鱼效应-黄金正弦改进WOA，弥补WOA在解决复杂优化问题时收敛速度慢、收敛精度低的不足；③利用IWOA(improved whale optimization algorithm)优化Elman神经网络的初始阈值与权值，提高Elman神经网络的泛化能力与预测精度，强化网络稳定性，避免输出结果陷入局部最优；④基于IWOA-Elman神经网络构建碾压速度异常值修正模型，保障数据的完整性与可靠性；

(3)将本文提出的碾压速度异常值检测与修正方法应用于选定的心墙区凸块碾压机速度监控数据中，验证本文方法的有效性，并通过与箱线图法及Elman神经网络、BP神经网络的对比，验证本文异常值检测与修正方法的优越性。

3 碾压速度异常值检测与修正方法

3.1 基于Kmeans-EMD的碾压速度异常值检测

3.1.1 基于Kmeans算法的异常值初步定性检测 Kmeans算法又称K均值算法，是一类典型的基于距离的聚类算法，因结构清晰、收敛速度快而被广泛应用于聚类及异常值检测问题中[22-23]。

Kmeans算法的基本思想是在碾压速度数据集D={X1，X2，…，Xm}中选取K个样本作为簇心，即质心Zj(j=1，2，…，K)，进而计算各样本Xi(i=1，2，…，m)与K个质心间的欧式距离dij，并将各样本划分至所距最近质心的所在簇，得到K个簇Cj(j=1，2，…，K)，然后逐步计算新簇质心，并重复上述步骤，直到聚类准则函数收敛，聚类准则函数如式(1)所示。

(1)

E值表征了聚类后所得各簇的最小化平方误差，E值越小则簇中碾压速度数据围绕质心越紧密，簇内相似度越高，聚类效果越好，因此各簇内碾压速度数据均应表现出聚集性，但异常值会因不满足碾压速度的基本变化特征而偏离质心位置，表现出离群性，故可结合这一特性实现异常值的初步定性检测，从而弱化异常值对EMD分解结果的影响。

3.1.2 基于EMD的异常值精细定量检测 EMD是一种针对非线性、非平稳时间序列的自适应分解方法，在使用时无需设定任何基函数，仅依托序列自身的时间尺度即可将数据分解为若干不同频率的子序列，即本征模态函数(intrinsic mode function，IMF)和代表趋势项序列的残差余项(residual，R)[24]。

EMD在应用时需确定碾压速度序列v(t)的均值vm(t)及v(t)与vm(t)间的差值h1(t)，若h1(t)满足：①极值点的数目与过零点的数目相等或至多相差1；②上、下包络线均值为0。则令c1(t)=h1(t)，并以c1(t)为IMF第一分量，若不满足，则视h1(t)为待分解序列v(t)，重复上述过程直至满足要求。而后，从v(t)中分离出c1(t)，得到余项序列r1(t)=v(t)-c1(t)，再令r1(t)为待分解序列，并依次重复上述步骤，得到c2(t)，c3(t)，…，cn(t)，若残差余项rn(t)为常数或单调函数，则分解结束，得到n个IMF分量和残差余项rn(t)。

IMF分量较原碾压速度序列有更简单的波动规律，其中，高频分量反映了碾压速度序列中的高频与噪声信息，残差余项R与低频分量则分别粗略和细致地描述了碾压速度序列的变化趋势。

为实现异常值的精细定量检测，本文首先利用经Kmeans算法剔除异常值后的碾压速度序列v(t)组成序列v′(t)；其次，利用EMD对v′(t)进行分解，得到v′(t)的各IMF分量及余项R；再次，由后至前选择m个分量进行叠加，构成序列m(t)，以弱化噪声影响，保留变化趋势；最后，分析v′(t)与m(t)间的偏离程度d(t)，d(t)的计算如式(2)所示，并定义偏离程度阈值d0，当d(t)>d0时认为该时刻对应的值为异常值。

(2)

3.2 基于IWOA-Elman神经网络的碾压速度异常值修正模型

3.2.1 IWOA简介 IWOA是WOA的改进，WOA是受座头鲸狩猎行为启发提出的一种智能算法，具体可参考Mirjalili等[25]的描述。WOA通过模拟座头鲸狩猎时的包围式捕猎、气泡网式捕猎和随机式捕猎行为搜索最优解，在寻优过程中所需参数少、全局收敛性强，相比粒子群算法、遗传算法等优化算法，不仅易于实现，亦能满足精度要求，适用于本文对Elman神经网络初始阈值和权值的优化[25-26]。

但本文对Elman神经网络初始阈值和权值的优化属多参数复杂优化问题，而WOA在解决此类问题时，仍存在收敛速度慢、收敛精度低、后期开发能力较弱的缺陷，且算法本身的趋同性易导致搜索陷入局部最优。

针对上述问题：

(1)本文利用混沌机制初始化WOA种群[27]，通过随机遍历搜索空间的方式强化种群个体的多样性，提高初始种群质量，强化算法的搜索效率与寻优能力，以避免因随机初始化种群造成的可行解搜索范围变大、搜索速度降低、寻优精度下降等问题。该方法在实现过程中首先随机生成实数向量Xi，而后根据公式(3)生成其余个体初始位置。

Xi+1=mod(Xi+1/5-(4π)-1·sin(2π·Xi),1)

(3)

式中：Xi为第i个体的位置；mod为求余函数。

(2)本文引入非线性收敛因子a[28]，以解决收敛因子若通过线性方式由2递减至0则难以适应实际优化搜索过程的问题，进而有效平衡全局与局部搜索，非线性收敛因子如公式(4)所示。

(4)

式中：a为收敛因子；t为当前迭代次数；tmax为最大迭代次数；μ为衰减系数，μ>0，本文取0.6。

(3)本文提出一种自适应惯性权重策略，使种群可以根据搜索情况改变收敛速度，以快速收敛至全局最优解。该策略可在搜索前期获得较大步长，提高搜索效率，而在后期获得较小步长，提高寻优精度，自适应惯性权重如公式(5)所示。

(5)

式中：w为惯性权重；t为当前迭代次数；tmax为最大迭代次数；wmin为惯性权重的最小值，本文取0.4；wmax为惯性权重的最大值，本文取0.9。

(4)本文结合鲶鱼效应策略[29]对WOA进行改进，若最优解在规定迭代次数内没有进化，则更新种群内适应度较差的90%个体的位置，以恢复种群活力，提高算法跳出局部最优的能力，避免算法早熟。其中，位置更新过程引入黄金正弦算法实现[30]，如公式(6)～(9)所示。

X(t+1)=X(t)·│sin(r1)│-r2·sin(r1)·D

(6)

D=│x1·Pt-x2·X(t)│

(7)

x1=-π+(1-V)·2π

(8)

x2=-π+V·2π

(9)

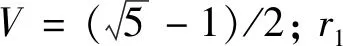
3.2.2 IWOA-Elman神经网络模型 本文以均方根误差(root mean square error，RMSE)作为适应度函数评价IWOA的寻优情况，并利用寻优结果优化Elman神经网络的初始阈值与权值[31-32]，以提高Elman神经网络的泛化能力，弥补传统Elman神经网络通过随机方式生成初始阈值与权值易导致模型训练过程收敛稳定性下降的不足，避免输出结果陷入局部最优，提高神经网络的预测精度，IWOA-Elman神经网络模型的构建步骤如图2所示，具体解释如下：

(1)初始化WOA参数并根据Elman神经网络拓扑结构确定鲸鱼群搜索维度，本文鲸鱼群搜索维度为Elman神经网络阈值与权值的数量和：

K=E·F+F·H+F+H

(10)

式中：K为鲸鱼群搜索维度；E为输入层神经元个数；F为隐含层神经元个数；H为输出层神经元个数。

(2)利用混沌机制初始化鲸鱼个体位置；

(3)计算各鲸鱼个体初始位置适应度，并记录当前适应度最优个体的所在位置X′及其适应度Y′；

(4)引入非线性收敛因子及自适应惯性权重，更新鲸鱼个体的a、w等参数；

(5)依据WOA包围式捕猎、气泡网式捕猎和随机式捕猎行为的执行条件，确定当前行为模式，得到鲸鱼个体更新后的位置；

(6)经位置更新后，再次确定各鲸鱼个体的适应度，并记录具有最优适应度个体的位置X及其适应度Y，若Y优于已有的Y′则更新Y′与X′，反之则进入步骤(7)；

(7)判断Y′在规定迭代次数下是否进化，若进化则进入步骤(8)，反之则引入鲶鱼效应-黄金正弦对适应度较差的90%个体的位置进行更新，再进入步骤(8)；

(8)则重复执行步骤(4)～步骤(7)，直到满足迭代终止条件时，认为算法已生成最优解，此时最优解保存于X′；

(9)利用最优解X′优化Elman神经网络的初始阈值与权值，实现IWOA-Elman神经网络模型的构建。

4 实例工程应用

以西南地区某心墙堆石坝心墙区凸块碾压机速度监控数据为研究对象，共采集到1 423个连续的碾压速度序列点，其碾压速度数据值=实际碾压速度(km/h)×100，在此基础上，利用本文所提方法开展碾压速度的异常值检测与修正。

4.1 异常值检测结果

对碾压速度而言，其异常值通常表现为异常大值或异常小值，而异常小值多由变换条带的正常工作流程导致，且异常大值对应的超速情况会使单位时间内填筑料的碾压功输入不足，相比变换条带的减速阶段更易导致填筑料压实不充分，从而影响压实质量评价结果[33]，故本文的异常值检测主要面向碾压速度中的异常大值，并基于Kmeans算法与EMD实现。

4.1.1 基于Kmeans算法的异常值检测结果 本文通过对碾压机工作状态(速度稳定、加速与减速)的区分与试验分析，判断当Kmeans算法簇个数为3时即可解释不同的数据情况，亦可确保聚类结果稳定，Kmeans算法异常值检测结果如图3所示。

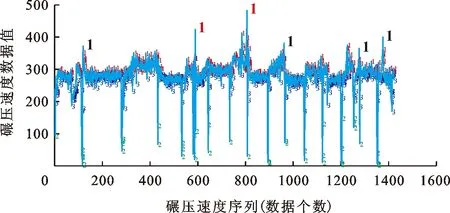
图3 基于Kmeans算法的碾压速度异常值检测结果

由图3可知，碾压速度中的异常大值均体现在1号簇，且图中放大的红色标号位置，即序列589和806位置为明显异常大值，可将其定义为异常值；而放大的黑色标号位置则为模糊异常大值，无法直接通过Kmeans算法判断，需经EMD的二次分析。

4.1.2 基于EMD的异常值检测结果 由于Kmeans算法仅能定性检测异常值，以弱化明显异常大值对EMD分解结果的影响，却无法实现对模糊异常大值的判断，故本文在将Kmeans算法检测出的异常值剔除后，利用EMD对组成序列v′(t)进行分解，共获得10个分量，包括9个IMF分量与余项R，如图4所示，进而利用选定的IMF分量与余项R构建新序列，并结合公式(2)进一步判断异常值位置，实现异常值的精细定量检测。

图4 碾压速度序列的EMD分解结果

根据前文3.1.2节中的描述与试验分析，本文选定m值为5，即利用后4个IMF分量与余项R构建序列m(t)，并确定偏离程度阈值d0为0.35。EMD异常值检测结果如图5所示，图5中圆圈对应的序列位置为异常值所在位置，黑色实线为利用IMF分量与余项R构建的序列m(t)。

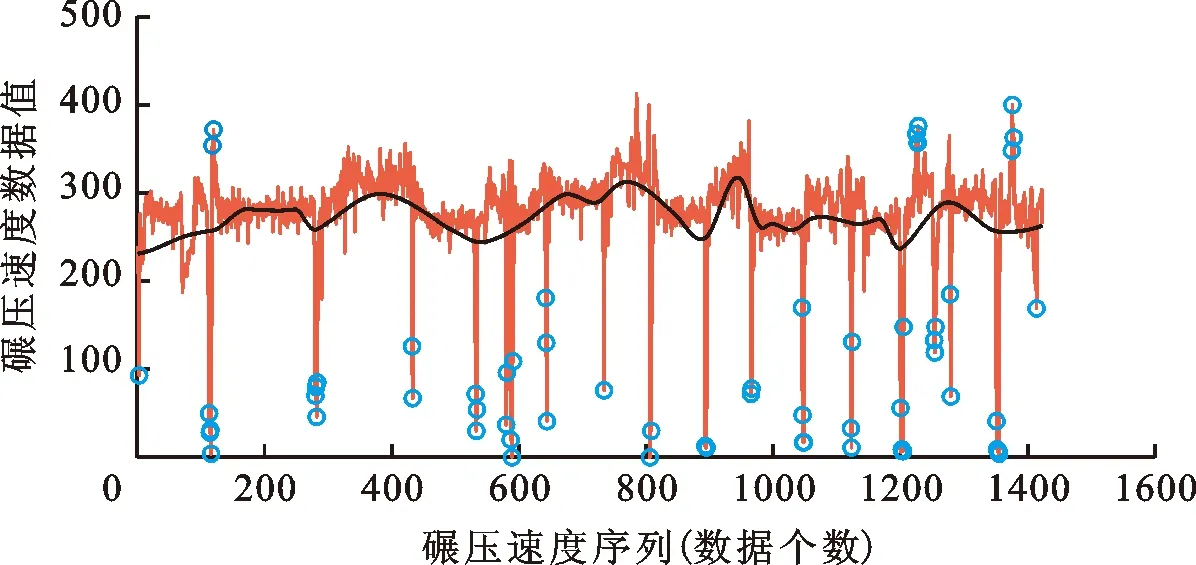
图5 基于EMD的碾压速度异常值检测结果

如图5所示，EMD异常值检测通过去除高频与噪声分量实现对碾压速度的滤波处理，有效避免了对异常大值的误判。EMD异常值检测结果表明碾压速度序列中118、120、1 225、1 226、1 227、1 228、1 375、1 376和1 378位置均为异常值，应予以剔除。

4.1.3 Kmeans-EMD对异常值检测的优势 本文以箱线图异常值检测方法[34]作为对比，论证Kmeans算法与EMD联合运用于异常值检测的优势。箱线图异常值检测结果如图6所示。本文所用碾压速度数据对应的箱线图上限与下限分别为351.5和219.5，即图6中两虚线之外的序列位置均为箱线图所检测的异常值。由图6可知，尽管箱线图可基于统计学原理实现异常值检测，却没有考虑碾压速度的时序变化特征，易将连续超速值均检测为异常值，故本文异常值检测方法具有更高的检测精度。

图6 基于箱线图的碾压速度异常值检测结果

4.2 IWOA-Elman神经网络异常值修正结果

为确定异常值位置下碾压速度的合理取值，以保障数据的完整性，强化数据的可靠性，本文构建了IWOA-Elman神经网络碾压速度异常值修正模型。设定鲸鱼种群数为10，最大迭代次数为500，规定迭代次数为20，Elman神经网络隐含层神经元为5，训练函数为traingdx，碾压速度数据总数为1 423。为实现对碾压速度序列的预测，并考虑到碾压速度序列预测组构建时不应过多影响原序列的完整性[35]，且前10个数据中不含异常值，本文以10个碾压速度序列为一组，将各组的10个碾压速度序列作为输入数据，预测下一组中第1个碾压速度数据值。经上述处理，本文共得到1 413组数据，规定前1 300组为训练集，后113组为测试集，输出序列中不包括原碾压速度序列中的前10个数据值。IWOA-Elman神经网络测试集输出结果如图7所示。

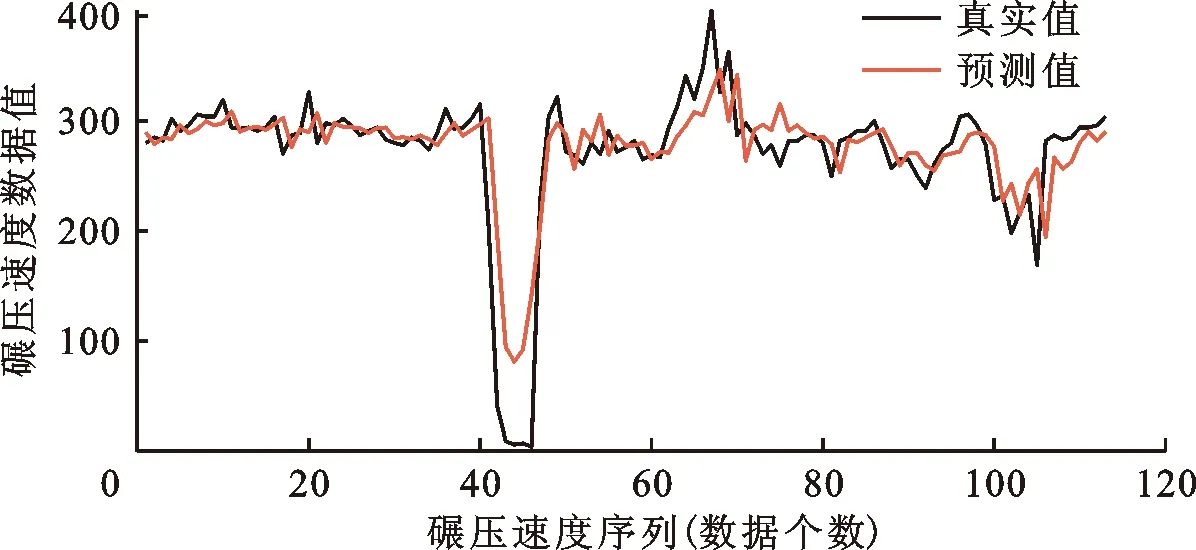
图7 IWOA-Elman神经网络碾压速度测试集输出结果

由图7可知，IWOA-Elman神经网络可较好拟合真实值情况，尽管变更条带的减速过程在数值表现上的时间相关性较弱，在一定程度上影响了IWOA-Elman神经网络的拟合效果，但相关性分析表明测试集相关系数仍达到0.907 75，且在与Elman神经网络及BP神经网络的对比中体现出优越性，相关系数对比结果如表1所示，即IWOA-Elman神经网络在碾压速度序列的拟合上具有较高的鲁棒性与拟合精度，其修正结果亦可有效体现碾压速度的时间相关性。

表1 不同神经网络形式的测试集相关系数对比

利用IWOA-Elman神经网络碾压速度异常值修正模型获取碾压速度序列中118、120、589、806、1 225、1 226、1 227、1 228、1 375、1 376和1 378位置的预测值并对原碾压速度序列进行替换，替换后各位置下碾压速度数据值分别为310.2、279.6、339.9、361.2、322.3、304.3、310.8、328.7、312.5、323.7及303.0。

为评价替换后的数据质量，对替换后的碾压速度再次进行Kmeans聚类，结果如图8所示。由图8可知，经异常值检测与修正后，碾压速度数据质量得到明显提升，不存在异常大值，可为压实质量高精度评价提供良好的数据基础。

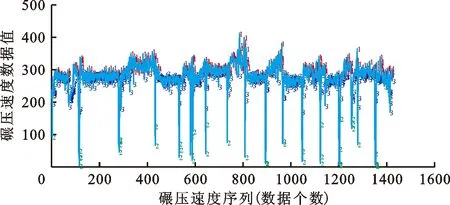
图8 以碾压速度修正值替换后Kmeans异常值检测结果

4.3 讨 论

本文研究在综合考虑碾压速度时序变化特征的基础上，实现了基于Kmeans-EMD的碾压速度异常值检测和基于IWOA-Elman神经网络的异常值修正，相较于传统方法，本文方法具有更高的异常值检测与修正精度，不仅可确保更好的数据完整性与可靠性，还可为压实质量高精度评价提供良好的数据基础，能有效弥补当前有关碾压速度数据异常值检测与修正研究的空白，提高了碾压速度的数据质量。但本文异常值检测与修正方法不适用于碾压速度缺失较多的状况，且由于碾压施工过程工艺情况复杂，其超速与减速阶段间可能存在复杂的相互影响，而本文仅通过单位时间内填筑料碾压功的输入情况判断异常值检测主要面向的数据类型，后续研究还需深入探讨碾压速度与压实质量间的相关关系，以准确界定碾压速度异常值检测的数据范围。

5 结 论

目前在大坝坝体填筑施工中，尚无碾压速度异常值的检测与修正方法，因而难以确保碾压速度的数据质量，还易导致压实质量评价精度的降低。针对这一现状，本文开展了基于Kmeans-EMD与IWOA-Elman的碾压速度异常值检测与修正研究，得到的主要结论如下：

(1)提出基于Kmeans算法与EMD的异常值检测方法：首先利用Kmeans算法对碾压速度进行聚类，通过将明显异常大值定义为异常值，实现对异常值的初步定性检测；再利用EMD对处理后的碾压速度序列进行分解，并通过选用的IMF分量与余项R构建新序列，实现基于偏离程度阈值d0的异常值精细定量检测。实例工程应用结果表明，Kmeans算法和EMD的联合运用相比箱线图法可更高精度地检测碾压速度中的异常值，有助于提高数据质量。

(2)构建IWOA-Elman神经网络碾压速度异常值修正模型：首先，利用混沌种群初始化、非线性收敛因子、自适应惯性权重与鲶鱼效应-黄金正弦改进WOA，弥补WOA在解决复杂优化问题时收敛速度慢、收敛精度低的不足；其次，利用IWOA优化Elman神经网络的初始阈值与权值，提高Elman神经网络的泛化能力，强化网络稳定性，避免输出结果陷入局部最优；最后，基于IWOA-Elman神经网络实现碾压速度的异常值修正，确保数据的完整性和可靠性。实例工程应用结果表明，IWOA-Elman神经网络的预测结果与原碾压速度数据间拟合情况良好，相关系数达到0.907 75，相比常规模型不仅可实现更有效的异常值修正，保障数据序列结构，还可为压实质量高精度评价奠定良好的数据基础。