投资型环境规制对绿色全要素生产率的非线性影响
2022-07-01范博凯
杨 书,范博凯,顾 芸
(1. 北京大学光华管理学院,北京 100871;2. 首都经济贸易大学城市经济与公共管理学院,北京 100070)
改革开放四十多年来,中国人均GDP 从1978 年的155 美元增加到2021 年的1.25 万美元,实现了历史性跨越。从经济学角度看,这个发展过程先后经历了要素驱动和投资驱动阶段,且正迈入创新驱动发展阶段,经济发展逐步从高速增长转向高质量发展阶段。经济高速增长是要素投资驱动型的粗放增长,与资源浪费、环境污染、生态破坏等问题相伴而行。为此,党的十八大报告提出要大力推进生态文明建设,努力建设美丽中国;党的十八届五中全会提出“创新、协调、绿色、开放、共享”的新发展理念;党的十九届六中全会提出“绿色成为普遍形态”的理念。为应对全球气候变化和促进绿色转型,习近平在第七十五届联合国大会上宣布中国将采取更加有力的政策措施,二氧化碳排放力争于2030年前达到峰值,努力争取2060 年前实现碳中和。《2030 年前碳达峰行动方案》进一步明确,到2025 年,非化石能源消费比重达到20%左右,单位国内生产总值能源消耗比2020年下降13.5%,单位国内生产总值二氧化碳排放比2020 年下降18%。显然,要实现绿色低碳转型目标,环境规制是重要举措之一。自第一次全国环境保护会议确立环境管理方针以来,中国环境规制政策经历了从无到有、从初设到完善、从附属到独立的过程,环境规制为我国生态文明建设提供了制度基础和保证机制。实际上,在高速增长和高质量发展两个不同阶段,经济发展模式的底层逻辑不同,故而环境规制的绿色转型发展影响具有差异性。因此,将资源和环境要素纳入绿色转型发展研究,探讨不同发展阶段的区域绿色发展特征,从不同视角揭示环境规制对绿色全要素生产率的影响机制,对于推动绿色高质量发展具有重要意义。
1 文献综述
环境规制与绿色全要素生产率关系的研究是一个热门话题。“波特假说”从动态角度出发,认为一定程度的环境规制可以激发企业的创新补偿效应,不仅能抵消遵循成本的损耗,而且能够产生技术扩散和结构升级效应,进而促进经济增长[1]。此后,国内外学者纷纷利用不同国家、地区或产业的数据检验“波特假说”。从现有文献来看,环境规制与绿色全要素生产率间存在何种关联未有定论,主要包括“促进说”“抑制说”和“非线性说”。如高艺等[2]采用空间计量模型实证发现,公众参与型环境规制对绿色全要素生产率起显著促进作用,而命令控制型和经济激励型环境规制对绿色全要素生产率起抑制作用。关海玲等[3]测算了2005—2017 年中国省级工业绿色全要素生产率,并基于空间杜宾模型证实环境规制与工业绿色全要素生产率呈正相关关系。
“非线性说”则考虑了环境规制与绿色全要素生产率之间的非线性关系,认为环境规制对绿色全要素生产率的影响存在倒“U”型关系或“U”型关系,即环境规制强度对绿色全要素生产率呈先促进后抑制或先抑制后促进的作用。例如,李玲等[4]将制造业分为重度污染、中度污染和轻度污染行业,实证发现不同行业的环境规制强度与绿色全要素生产率之间均存在倒“U”型关系。殷宝庆[5]认为中国省级环境规制强度与制造业绿色全要素生产率整体上呈倒“U”型关系,且这种关系在清洁型和非清洁型制造业中均成立。刘和旺等[6]和蔡乌赶等[7]则认为中国省级层面市场型环境规制对绿色全要素生产率的倒“U”型影响更突出。此外,宋典等[8]认为即使在技术引进、模仿创新路径下,环境规制对工业绿色全要素生产率亦呈现先促进后抑制的作用。分区域来看,李德山等[9]认为我国东、中、西及东北部城市环境规制与绿色全要素生产率间皆呈倒“U”型关系。
上述研究认为环境规制与绿色全要素生产率间存在倒“U”型关系,另有研究认为两者间存在“U”型关系。如罗能生等[10]基于动态空间杜宾模型实证发现中国省级“治理投入型”环境规制与绿色全要素生产率之间存在“U”型关系。高苇等[11]基于省级矿业发展层面的研究发现,命令控制型和市场激励型环境规制对矿业绿色发展表现出先抑制后促进的直接效应。许梦博等[12]测算了2002—2018 年工业绿色全要素生产率,并基于动态空间计量模型实证发现中国中部和西部地区的费用型规制与工业绿色生产率之间呈“U”型关系。此外,吴磊等[13]认为公众自愿型和市场激励型环境规制短期抑制绿色全要素生产率增长,而长期则起促进作用。
在环境规制的衡量方面,部分研究以单一指标表征,另有部分研究则讨论了执行主体不同的异质型环境规制,相关指标的选择则各不相同。例如,许梦博等[12]划分了命令控制型、费用型以及投资型环境规制;关海玲等[14]划分了正式和非正式环境规制;肖权等[15]划分了命令控制型、市场激励型以及自主型环境规制;吴磊等[13]划分了命令控制型、市场激励型以及公众自愿型环境规制。其中,以“(工业)环境污染投资总额”为代表的投资型环境规制是这类研究的关注重点,也更能直接反映政府治理环境的成本。
关于绿色全要素生产率的测算。新近研究多采用以数据包络分析法(DEA)为代表的非参数方法,比如吴翔[16]采用三阶段DEA模型和Malmquist指数相结合的方法测算了绿色经济效率,该方法的优点在于无须事先设定函数形式和不需考虑环境要素的价格信息。然而,传统的DEA模型不能解决非期望产出问题。通常非期望产出的处理方法主要有投入产出转置法、倒数转换法、正向属性转换法和方向距离函数法等,其中部分研究将非期望产出作为投入或者取倒数作为产出纳入生产效率评价模型[17-18]。为解决这一问题,Chung 等[19]提出了DDF 模型,但该模型假设期望产出的扩张以及投入要素和非期望产出的缩减严格等比例,这可能导致“松弛偏误”[20]。因此,非径向方向距离函数(NDDF)被发展出来,放松了等比例变化的假设条件[21-22]。此外,基于松弛变量的、非径向、非角度的SBM模型也可解决“松弛偏误”问题,不少学者利用该模型测算绿色全要素生产率。此外,以随机前沿分析方法(SFA)为代表的参数方法和索罗余值方法亦可测算绿色全要素生产率。总体而言,相较于索罗余值法和随机前沿分析法,基于DEA方法的全要素生产率测算考虑了多投入、多产出的线性规划思想,更易比较决策单元与技术进步前沿面之间的距离,一定程度上摆脱了索罗余值法等的先验生产函数设定偏误,因此受到众多研究者的青睐。
已有关于环境规制与绿色全要素生产率的研究尚存一定局限性:一是不同主体的环境规制对绿色全要素生产率的作用机制存在差异,“一概而论”的研究未能深入剖析投资型环境规制——政府主导的环境规制对绿色全要素生产率的异质影响机制;二是多数研究忽视环境规制的空间外部性,即忽略了环境规制影响绿色全要素生产率的空间效应;三是绿色全要素生产率的测算有待完善,相关研究较少综合考虑技术进步因素、人力资本和创新投入,也较少考虑碳排放问题。鉴于此,文章可能的贡献在于:一是针对性地研究投资型环境规制与绿色全要素生产率之间的影响机制,采取空间计量模型和多重门槛模型分析投资型环境规制对绿色全要素生产率的非线性影响,分别检验考虑空间效应后和考虑门槛效应后的影响机制异同;二是以2012年为分界点,区别看待经济发展的高速增长阶段和高质量发展阶段,探讨其不同发展阶段的非线性影响特征;三是在绿色全要素生产率的测算方面采用考虑松弛变量的SBM 模型,纳入人力资本投入和创新投入,并引入大气污染与碳排放等非期望产出,一定程度上提高了绿色全要素生产率的测算精度。
2 理论机制与特征事实
2.1 理论机制分析
环境规制影响绿色全要素生产率的理论机制比较复杂,一方面依据Porter 等[1]提出的“创新补偿效应”,一定程度的环境规制有利于企业的技术创新升级、降低环境污染,进而提升绿色全要素生产率;另一方面,Lanoie等[23]提出“遵循成本效应”,环境规制将直接提高企业生产成本,部分挤出创新投资,长期来看并不利于绿色全要素生产率增长。故当环境规制的执行成本大于创新补偿时,环境规制将不利于提高绿色全要素生产率,而反之则有利。然而,环境规制与绿色全要素生产率在企业层面的影响机制,可能并不适用于探讨区域层面上以政府为主导的投资型环境规制问题。因此,文章基于区域内部和区域间双视角分析投资型环境规制与绿色全要素生产率间的影响机制。
从区域内部来看,投资型环境规制与绿色全要素生产率间可能存在非线性关系。一方面,投资型环境规制可以通过改善生态环境提高绿色全要素生产率,抑或由于环境治理投资效率较高,间接提高绿色全要素生产率。一般而言,单位GDP 能耗越高,环境污染越严重,投资型环境规制对绿色全要素生产率促进作用的边际贡献更大。另一方面,投资型环境规制可能囿于无法满足环境治理需要,较难通过改善生态环境来提高绿色全要素生产率;抑或投资型环境规制强度过高,政府所负担的治理环境成本加重,挤占政府财政的生产保障支出,从而不利于提高绿色全要素生产率。通常来说,单位GDP 能耗下降则环境污染随之改善,相应投资型环境规制的边际作用可能下降,此时过重的环境规制手段不利于绿色全要素生产率的提高。从区域间来看,本地区投资型环境规制和绿色全要素生产率可能会对其他地区的绿色全要素生产率产生正向溢出效应或虹吸效应。一方面,投资型环境规制可以通过改善本地生态环境吸引其他地区的企业或劳动力,使得其他地区的企业数量下降或劳动力减少,其他地区的经济总量趋于下降,从而不利于其他地区的绿色全要素生产率提高。另一方面,投资型环境规制可能通过改善本地生态环境吸引更多清洁型产业和创新型企业,提高本地人力资本积累,提升本地知识溢出强度,从而通过知识溢出渠道促进其他地区的绿色全要素生产率提高;考虑到大气循环和水循环等自然因素的区域关联性,本地生态环境的改善可能同时优化了其他地区的生态环境,间接提高其他地区的绿色全要素生产率。当然,绿色全要素生产率的空间效应可能由于经济集聚机制或知识溢出效应,引致其他地区绿色全要素生产率增长乏力或协同增长。
综上,文章提出如下命题:①投资型环境规制与绿色全要素生产率之间可能存在非线性关系;②不同单位GDP 能耗条件下,投资型环境规制对绿色全要素生产率的影响具有异质性影响特征;③本地区投资型环境规制强度的增加有可能损害或提高其他地区的绿色全要素生产率;④本地区绿色全要素生产率对其他地区绿色全要素生产率可能产生溢出效应或虹吸效应。
2.2 特征事实分析
不同发展阶段和不同地区的投资型环境规制具有差异性。从时间角度来看,中国工业污染治理完成投资额占GDP 比重在2001—2011 年间呈“U”型变化趋势,而在2012—2019 年间则大体上呈下降趋势。可能的原因是,党的十八大之后,国家顶层设计治理环境污染问题,由“先污染后治理”的老路走向节能减排绿色发展之路,加大了污染减排、绿色技术创新和发展绿色产业等污染源头上的防治力度。从区域角度看,东部地区的工业污染治理完成投资额占GDP 比重自2011 年起低于中西部地区,与中国东部与中西部地区的产业结构分布特征以及绿色技术应用现状相吻合(图1)。基于此差异性特征,后续研究应开展相应机制的时空异质性分析。
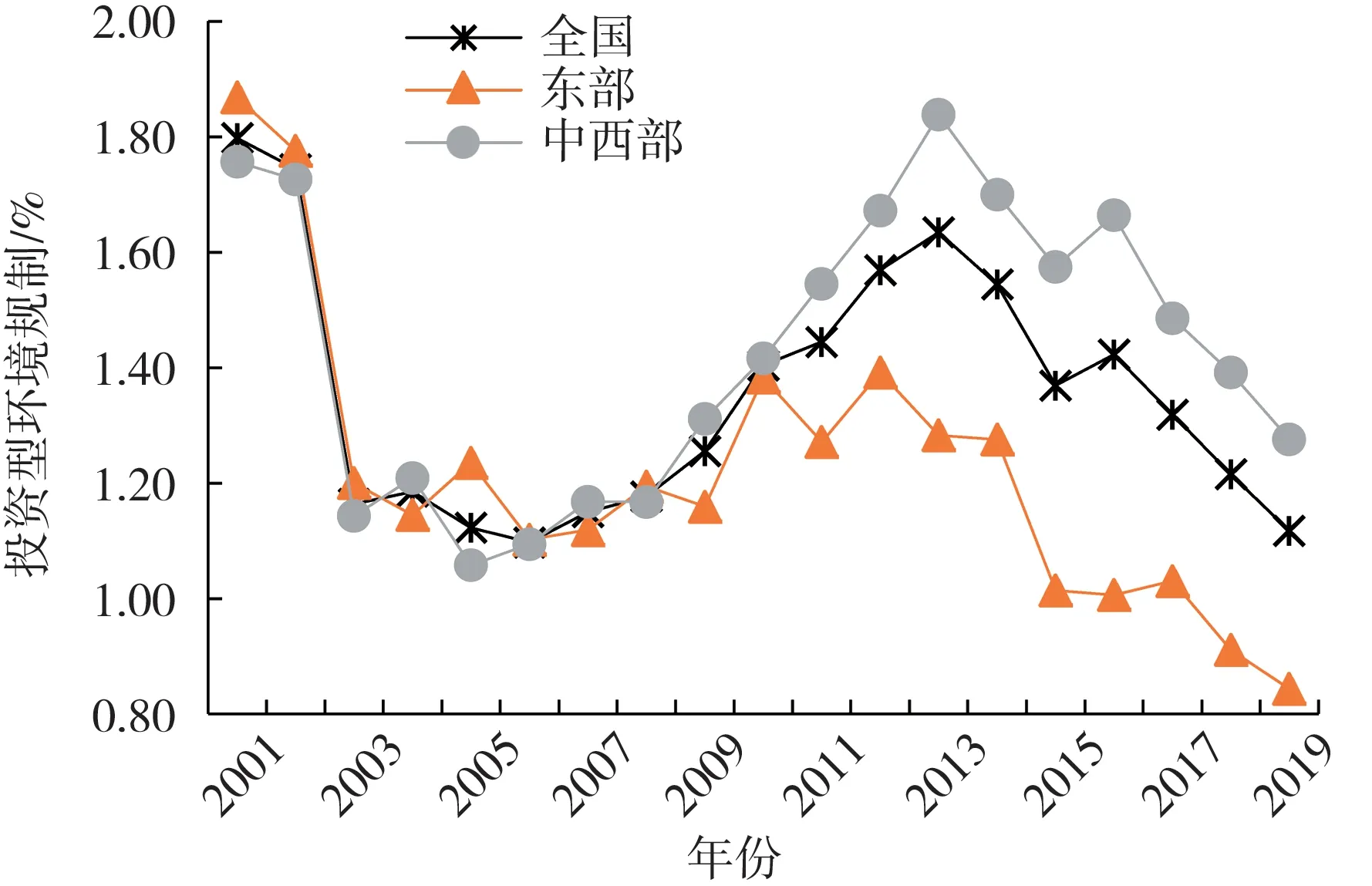
图1 投资型环境规制变化趋势图(2001—2019年)
进一步地,相关性分析表明,投资型环境规制与绿色全要素生产率之间存在非线性关系(图2)。具体来看,2001—2019年间,随着投资型环境规制强度提高,绿色全要素生产率呈由上升转为下降的倒“U”型趋势,且投资型环境规制与绿色全要素生产率在2001—2011年和2012—2019年两个时段均呈现倒“U”型关系。当然,这种关系是否可信仍需进一步实证检验。
3 绿色全要素生产率测算与分解
3.1 基于SBM模型的绿色全要素生产率测算方法
由于经典径向DEA 模型要求投入要素按固定比例同步增长,难以衡量生产要素之间因发展环境、发展阶段不同而导致的具有显著差异性的边际技术替代率,因此忽略了超大规模市场下发达地区与落后地区的增长路径不统一的问题。文章借鉴Tone[24]提出的基于松弛变量的SBM 模型,该模型对每种要素均增加松弛变量的设定,能够较好地解决处于不同生产阶段的各要素之间投入变动不等比例问题。具体来说,以省域范围作为基本决策单元,假定在同一时间段内,每一决策单元均使用M 种投入要 素,生 产 出N 种 期 望 产 出y =,以 及J 种 非 期 望 产 出

其中:i表示对应的省级单位,zti表示各时间截面上观测值的权重,zti= 1,zti≥0 表示可变的规模报酬(VRS)。借鉴Fukuyama 等[20]SBM 模型处理方法,在VRS 条件下,构建包含非期望产出的当期SBM 方向性距离函数。若将StV各要素权重变量和为1的约束去掉,则退化为CRS条件下的方向性距离函数。


3.2 指标选取与数据来源
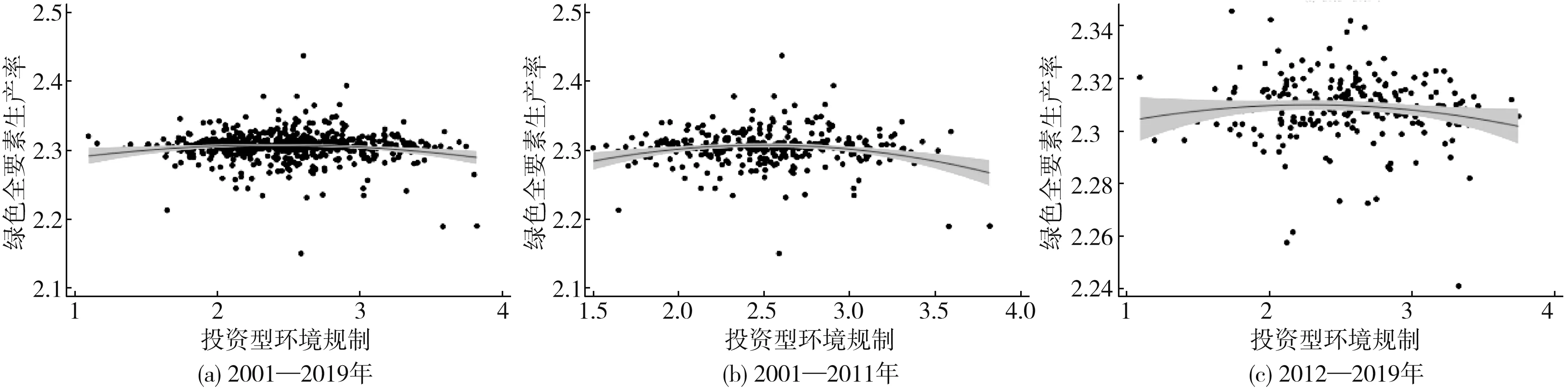
图2 投资型环境规制与绿色全要素生产率相关性拟合图
绿色全要素生产率测算的准确性主要受投入、产出指标选择的影响,依据已有研究探讨,同时为降低因指标选取片面、缺失等因素造成测算结果失真的可能性,投入指标选择以兼顾全面性和美好生活导向性为宗旨,纳入三类经济要素和一类资源要素,产出指标包含期望和非期望两大类,同时兼顾了总量和结构特征。具体来说:①期望产出。借鉴多数文献指标选择经验,选用各省份以1985 年为基期的可比价GDP 衡量。②非期望产出。有关非期望产出的选择,不同文献之间差异性较大,但主要集中于工业污染排放层面,如考虑工业三废排放[26]、涉及工业SO2和COD[27]、仅考察二氧化碳排放[28]、仅考虑工业SO2[29]。为实现碳达峰和碳中和目标,同时考虑到大气污染已成为环境污染的主要组成部分,若经济发展的非期望产出仅局限于工业污染排放则偏离高质量发展的初衷,因此效率测算模型中非期望产出应包含碳排放和PM2.5浓度,以同时考察经济发展伴随的气候变化和环境污染双重非期望约束,其中PM2.5原始浓度气象栅格数据来自达尔豪斯大学,碳排放数据来自CEADs 数据库。③劳动要素投入。采用各省份城镇就业人员数指标代理,数据来自《中国劳动统计年鉴》,部分缺失数据已做线性插值处理。④资本要素投入。资本投入分为两类,一类为经固定资产投资形成的固定资本存量,一类为人力资本存量,分别用以表征绿色效率变动中的实物资本和知识资本作用强度。固定资本存量采用单豪杰的计算方法所得;人力资本存量数据来自《中国人力资本指数报告》数据库,该指标在衡量人力资本方面具有更高的准确性,且更贴近实际的人力资本存量值。⑤技术要素投入。与现有不考虑技术要素投入的效率测算方式不同,在此考虑以专利授权量衡量的技术投入对产出效率的影响,以期测算结果更加真实。分省专利授权量数据来自国家知识产权局。⑥资源要素投入。经济活动与能源消耗密切相关,采用能源消耗总量代理经济发展中的资源要素投入量,数据已折算为标准能源单位,数据来自《中国能源统计年鉴》。文中,东部、中部和西部地区的划分依据参照国家统计局统计制度及分类标准。其中,东部地区包括北京、天津、河北、辽宁、上海、江苏、浙江、福建、山东、广东和海南11 省份;中部地区包括山西、安徽、江西、河南、湖北、湖南、吉林和黑龙江8 省份;西部地区包括内蒙古、广西、重庆、四川、贵州、云南、西藏、陕西、甘肃、青海、宁夏和新疆12省份。囿于数据可得性,研究不涉及港澳台地区。
3.3 测算结果及分解分析
表1展示了2001—2011年和2012—2019年两个阶段中国绿色全要素生产率(GTFP)增长率、纯效率变动(TECH)、技术进步(BPC)和规模效率变动(SECH)。经济进入新常态(2012 年)前后比较可知,全国绿色全要素生产率增长率由0.1%增至0.62%,涨幅约为520%,其中技术进步的全国均值由负转正,是其增长的主要动力。该测算值低于相关文献结果[28,30-31],主要原因有二:其一是相关文献忽略了创新和人力资本对经济增长的贡献,其绿色全要素生产率测算结果包含两者的增长贡献,故其估算值高于实际值;其二是研究区间不同,多数研究未探讨新常态前后高速增长阶段和高质量发展阶段的特征差异。实际上,不同发展阶段绿色全要素生产率增长的驱动机制并不相同,如高速增长的2001—2011年阶段,规模效率变动是绿色全要素生产率增长的主导动力,西部绿色全要素生产率增长较快、东部次之、中部均值为负;2012 年后的高质量发展阶段,技术进步成为绿色全要素生产率增长的主导动力,中部绿色全要素生产率增长由负转正,且居于首位,西部次之,东部第三。综合而言,在高质量发展阶段,绿色全要素生产率快速提升且省域间差距缩小,技术进步主导全国绿色全要素生产率增长。
4 基于空间计量模型的实证检验
4.1 空间计量模型选择
根据理论机制分析,投资型环境规制对于绿色全要素生产率的影响具有空间外部性,在此采用空间计量模型检验投资型环境规制对绿色全要素生产率的空间影响。空间计量模型的一般形式为:
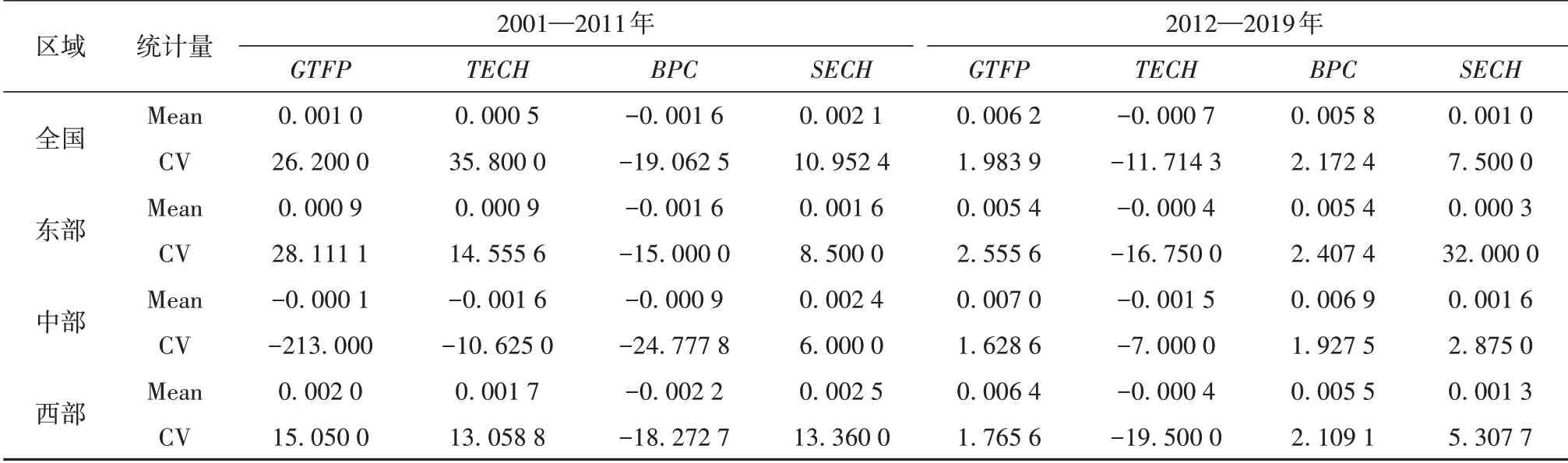
表1 中国绿色全要素生产率分时间段描述

当λ = 0,上式简化为SDM 模型;当λ = 0,且δ = 0,则为SAR模型;当τ = 0,且δ = 0,则为SAC模型;当τ = 0时,则为SDEM 模型;如果τ=ρ= 0,且δ = 0,则为SEM 模型。ρ为空间自相关系数;δ表征解释变量空间效应强度;λ为空间误差自相关系数;vit为随机干扰项;w′i为空间权重行向量。在空间权重矩阵的选择上,采用Queen邻接权重矩阵和地理距离权重矩阵。地理距离权重矩阵的元素取值随地区间空间距离增加呈指数形式衰减,具体设定如下:

其中:δ为空间关联的距离衰减参数,在此取值为1;dij为i省省会城市到j省省会城市的欧氏距离。
4.2 变量选取与数据来源
文章主要考察投资型环境规制对绿色全要素生产率的影响,因此核心解释变量为投资型环境规制。罗能生等[10]、许梦博等[12]选取(工业)环境污染投资总额这一绝对量指标衡量“治理投入型环境规制”或“投资型环境规制”,该指标与地方GDP总量密切相关,故不能较好地反映地区的投资型环境规制水平。此外,考察中国污染排放结构不难发现,以重工业和能源业为主的工业污染是我国污染排放的最主要来源,因此针对工业的污染治理投资对于考察中国整体的投资型环境规制具有良好代表性。鉴于此,文章借鉴杨丹等[32]的研究,以工业污染治理完成投资额占GDP比重衡量投资型环境规制(environ_r)(下文简称为“环境规制”),其中的工业污染治理完成投资包含了工业废水、废气、固体废物、噪声等治理项目的投资;同时,考虑到投资型环境规制与绿色全要素生产率之间可能存在非线性关系,在计量模型中一并纳入投资型环境规制二次项。
控制变量主要选取衡量经济发展能源依赖强度的单位GDP能耗(energy_g)、劳均研发支出(rd_l)、劳均人力资本(human_e)、人力资本投入结构(human_c)、创新质量(patent_q)、创新产出效率(patent_e),同时纳入创新产出效率与技术合同成交总额(pat)交互项(patent_e×pat)考察创新成果转换效率对绿色全要素生产率的影响。其中:①已有文献对于研发强度的设定因各有侧重而不尽相同,借鉴杨林等[33]以结构指标衡量单位产值研发强度的思想,以研发支出与城镇就业人员比值衡量劳均研发支出(rd_l),衡量全社会的平均研发强度。②周茂等[34]证实在物质资本匮乏条件下,人力资本的扩张可通过技术进步和要素再配置渠道显著促进制造业出口升级,且已有文献证明技术进步具有绿色偏向性[35],为检验人力资本与物质资本相对结构变化对绿色全要素生产率的影响,以实际劳动力人力资本存量与实际物质资本存量比值代理人力资本投入结构(human_c)变量。③人力资本水平反映了劳动力模仿技术、吸收知识和创新创造的能力,是衡量劳动力技能水平较为合适的代理指标[36],以人力资本与城镇就业人员数的比值代理劳均人力资本(human_e)。④借鉴黎文靖等[37]、李延喜等[38]的研究经验,创新质量(patent_q)以发明专利申请量与专利申请量比值衡量,创新产出效率(patent_e)以专利授权量与R&D人员全时当量比值衡量。
此外,文章还控制了每单位GDP 的外商投资企业投资总额、市场化指数、第二产业增加值占GDP 比重、人均GDP、城市生活成本指数、政府财政支出占GDP 比重等可能的影响因素,以求最大限度地避免遗漏变量。相关研究数据来自《中国统计年鉴》《中国环境统计年鉴》、中央财经大学《中国人力资本指数报告》和CNRDS 数据库;市场化指数[39]来自《中国分省份市场化指数报告(2018)》,部分缺失数据使用报告推荐计算方法插补完善;城市生活成本指数来自《中国人力资本指数报告》[40]。
4.3 空间相关性分析
经济变量具有空间相关性是空间计量模型顺利开展的前提,在此采用多权重面板数据Moran’sI指数检验中国省域绿色全要素生产率及其主要影响因素是否具有空间相关性。表2展示相关结果,中国省域绿色全要素生产率及其主要影响因素均呈现较强且显著的空间正相关性,集聚特征明显。其中,GTFP的空间相关性在不同空间权重测度下的结论保持稳健;环境规制(environ_r)的空间相关性相对较弱,Queen邻接权重空间相关强度小于地理距离权重;单位GDP能耗(energy_g)的空间相关特征最强;以劳均研发支出(rd_l)衡量的知识溢出的空间相关性仅次于能源消耗;劳均人力资本(human_e)表现出较强的空间集聚特征。
4.4 基准回归结果分析
为准确刻画环境规制对绿色全要素生产率的空间影响,依次采用邻接权重和距离权重下的SAR、SEM 和SDM模型估计相关参数,结果见表3。环境规制的一次项系数显著为正,二次项系数显著为负,这一结果在各类模型中均保持稳健。可见,在全国层面上,环境规制与绿色全要素生产率存在倒“U”型关系,适当的环境规制有助于提高绿色全要素生产率,但超过最优环境规制强度后(工业污染治理完成投资额占GDP 平均比重为1.35%),其对绿色全要素生产率的改善功效逐步衰减。如对于河北、山西、内蒙古、青海等“生态欠账”积累已久省份,短期内较强的环境规制能够显著降低污染排放,但对改善绿色全要素
生产率的作用有限。从列(1)—列(2)的空间滞后项来看,其系数分别为0.158 和4.772,且通过了5%和10%的显著性水平检验,表明本区域绿色全要素生产率与其邻近地区(相邻和距离相近的周边区域)的绿色全要素生产率之间存在空间互动机制。从列(3)—列(4)的空间误差系数λ来看,其估计值分别为0.177和5.665,表明地理相关权重吸收的空间误差冲击正向促进绿色全要素生产率。此外,基于地理距离权重测得的分省绿色全要素生产率空间效应半径约为465 km,空间误差冲击的距离衰减半径位于90~120 km和410~491 km区间内。

表2 2001—2019年相关变量Moran’s I指数

表3 空间计量回归结果——基准回归
从控制变量估计结果来看,单位GDP能耗(energy_g)和人力资本投入结构(human_c)的系数显著为负,表明单位GDP能耗越高和人力资本投入结构越差,绿色全要素生产率则越低;劳均人力资本(human_e)、创新质量(patent_q)和创新产出效率(patent_e)的系数显著为正,表明劳均人力资本、创新质量和创新产出效率正向促进绿色全要素生产率增长。创新成果转换效率对绿色全要素生产率的促进机制尚未体现。
SDM 模型估计结果显示,邻地环境规制增强显著促进本地绿色全要素生产率增长,而在距离权重刻画下这一影响强度由正转负且不显著。一定程度表明相邻区域间的环境规制更多呈现“以邻为伴”模式,有利于本地绿色发展,而在较大空间范围内距离相近区域间的环境规制可能呈现“以邻为壑”模式,阻碍本地绿色发展;邻近地区单位GDP能耗的升高有利于本地绿色全要素生产率提升,即增大与邻近区域间经济发展的能源依赖落差,降低本地能源依赖强度,有助于实现本地绿色增长;邻近地区劳均人力资本增强显著抑制本地绿色全要素生产率增长,表明人力资本的虹吸效应不利于区域绿色协调发展;邻近地区劳均研发支出增大显著促进本地绿色全要素生产率增长,研发支出扩张引致的知识溢出有利于区域绿色协调发展。综上而言,环境规制的空间协同治理显著促进本地绿色全要素生产率提升,强化知识溢出渠道、合理配置人力资本和环境规制协同治理是促进中国绿色全要素生产率增长的有效渠道。
4.5 稳健性检验
为确保研究稳健性,将技术要素投入的专利授权量更替为专利申请量,GTFP值由全局GML指数更替为相邻参比GML指数,重新估计相关参数以检验实证结论的稳健性。从稳健性检验结果来看(限于篇幅,留存备索),environ_r和environ_r2的估计结果与基准回归结果一致,即环境规制与绿色全要素生产率呈现倒“U”型关系。同时,其他控制变量和空间效应的估计结果与基准回归结果也基本一致,表明研究结果较为稳健。
4.6 时空异质性分析
为探讨环境规制对绿色全要素生产率的时空异质性影响,在此依据发展阶段和地理区位划分子样本,借助空间杜宾模型分析相应机制的时空异质性。
由表4 可知,在高速增长阶段(2001—2011 年)和高质量发展阶段(2012—2019 年),环境规制及其二次项系数与基准回归结果基本一致,但在高速增长阶段,投资型环境规制对绿色全要素生产率的促进强度高于高质量发展阶段,这意味着高质量发展阶段的绿色全要素生产率提高将愈发依赖创新等其他影响因素。此外,在高质量发展阶段,邻近地区绿色全要素生产率的提升显著促进本地绿色全要素生产率增长,这一促进强度高于高速发展阶段。这一经验证据表明,高质量发展阶段的绿色全要素生产率具有更突出的空间依赖特征,空间一体化的绿色发展是这一阶段的主要特征。

表4 不同发展阶段和不同区域的空间杜宾模型回归结果
分区域来看,东部和中西部地区的environ_r 和environ_r2系数方向与基准回归结果基本一致,且中西部的回归系数明显高于东部。这一证据表明,环境规制对绿色全要素生产率的影响与区域经济发展水平密切相关,经济发展水平相对落后地区的绿色全要素生产率受投资型环境规制的影响较大,而经济发展水平相对发达地区的绿色全要素生产率受创新等其他因素的影响更大。综合而言,环境规制对绿色全要素生产率的影响具有非线性时空异质性特征。
5 基于多重门槛模型的实证检验
5.1 多重门槛模型设定
根据理论机制分析,经济发展的能源依赖特征是影响投资型环境规制功效发挥的重要因素。单位GDP能耗是反映地区经济发展能源依赖强度的良好指标。此外,单位GDP能耗在一定程度上亦可反映绿色技术进步水平和产业结构优化特征,即单位GDP能耗越低,意味着地区绿色技术进步水平越高,高能耗产业比重越小。因此,文章以单位GDP 能耗作为门槛变量,采用多重门槛模型检验环境规制影响绿色全要素生产率的影响机制,计量模型设定如下:

式中:下标i、t分别表示省份和年份;ui和γt分别表示个体和时间固定效应,为保证回归结果的稳健,采用了仅省份固定、省份时间双向固定两种模型;εit为随机干扰项。y为被解释变量,即绿色全要素生产率;Xit为控制变量。energy_git为门槛条件变量,即单位GDP 能耗;th表示门槛值;I(·)为示性函数,当energy_git和th 满足括号内条件时,取值为1,否则为0。
5.2 回归结果分析
表5报告了多重门槛模型的回归结果,列(1)—列(3)仅控制省份固定效应,列(4)—列(6)控制省份、时间双向固定效应。列(1)和列(4)中的单一门槛模型结果显示,跨过门槛值后,environ_r的回归系数由显著为负转为不显著为负;列(2)和列(5)的双门槛模型结果显示,跨过第二门槛值后,environ_r 的回归系数由显著为正转为不显著;列(3)和列(6)的三重门槛模型结果显示,当跨过第三门槛值时,environ_r 回归系数的有效大小未出现显著变化。综合来看,当energy_g>3.337 时,环境规制对绿色全要素生产率的影响并不显著;当energy_g 位于3.337~1.662 区间时,环境规制对绿色全要素生产率的影响显著为正;当energy_g<1.662 时,即低于每万元GDP 消耗0.53 t 标准煤,环境规制对绿色全要素生产率的影响显著为负。换言之,随着单位GDP能耗的下降,环境规制对绿色全要素生产率的影响由不显著转为显著,且由积极影响转为消极影响。在现实中,随着《完善能源消费强度和总量双控制度方案》和《2030年前碳达峰行动方案》的落实,以投资型环境规制提升绿色全要素生产率的发展模式逐步式微。需要注意的是,2020 年中国每万元GDP 消耗0.49 t标准煤,已低于0.53 t标准煤门槛值。

表5 多重门槛模型回归结果
6 结论与建议
文章立足生态文明建设要求和绿色发展理念,首先在分析投资型环境规制影响绿色全要素生产率的理论机制基础上,基于纳入碳排放、PM2.5等非期望产出的SBM模型,测算2001—2019年省级层面绿色全要素生产率,并从纯效率、技术进步和规模效率角度分解三者贡献,揭示其不同发展阶段的驱动特征差异;而后针对环境规制与绿色全要素生产率间具有非线性关系的特征事实,基于SAR、SEM 和SDM 空间计量模型和多重门槛模型,分析投资型环境规制对绿色全要素生产率的非线性影响。研究发现:①全国层面,与2001—2011 年相比,2012—2019 年绿色全要素生产率增长从0.1%增至0.62%,技术进步是其主要驱动力;绿色全要素生产率的区域差距呈现缩小趋势。②在考虑空间效应后,投资型环境规制与绿色全要素生产率间存在显著倒“U”型关系,且相对于高速发展阶段和中西部地区而言,高质量发展阶段和东部地区的投资型环境规制影响更弱。③中国省域绿色全要素生产率具有显著的空间相关特征,投资型环境规制对绿色全要素生产率具有显著的正向空间促进效应,且不同时期、不同区域的空间促进效应具有异质性。④投资型环境规制对绿色全要素生产率的影响具有随能源依赖强度变动的非线性门槛效应,当单位GDP 能耗低于一定门槛条件后,弱化投资型环境规制方能促进绿色全要素生产率提高。
基于以上结论,尝试提出如下对策建议:
(1)科学把握、综合评估投资型环境规制对绿色全要素生产率的非线性门槛影响。一方面,要注重投资型环境规制政策的动态调整性,随着中国各省单位GDP 能耗的不断下降,各地政府应基于本地实际情况动态调整政策力度。另一方面,要注重投资型环境规制政策的区域异质性,对于能耗水平过高的区域而言,要合理选择投资型环境规制方式,坚决遏制高污染、高能耗项目盲目发展,落实能耗双控要求;对于能耗水平较高的区域而言,要充分发挥投资型环境规制的引领作用,以投资型环境规制撬动绿色转型发展;对于能耗水平较低的区域而言,要鼓励积极创新多元市场化环境规制方式,切实打好不同环境规制方式的“组合拳”,避免投资型环境规制政策的实施给当地经济发展带来治污负担,降低其挤出创新投资的风险。
(2)要充分利用投资型环境规制的空间溢出效应。一方面,要从国家宏观层面探索区域协同高效的环境规制和跨区生态补偿政策,构建国家层面支持、地方政府主导、区域间协同配合的空间联动体系,不断优化投资型环境规制政策举措,切实提升投资型环境规制效益,力争从制度上避免因经济利益冲突而导致的区域环境低效治理问题;另一方面,要探索区域间横向投资型环境规制合作机制,鼓励邻近区域构建环境规制的跨界合作网络体系,促进区域间自然资源的合理利用和环境治理的提质增效。
(3)要充分发挥绿色技术对于实现绿色高质量发展的根本性作用。一方面,强化绿色技术转型,重视绿色技术自主创新,探索制定支持绿色技术研发的长期性政策,加大低碳、负碳等绿色技术创新研发力度,支持绿色低碳技术的研发、推广和应用,推动数字经济的创新发展;同时加大对绿色低碳发展的宣传、推广工作,推动更多企业、市民参与到节能减排的实践中来,普及绿色低碳基础知识,倡导节能减排生活和生产方式。另一方面,要搭建绿色技术共商共建共享机制,引导企业主动参与创新链、产业链、价值链分工合作,推进创新链与产业链紧密融合,加快生产高端化、产品高端化、产业链高端化,促进产业发展向低碳、绿色、高端优化升级。
