超高压交叉线路空间电磁环境分析

马明智，杨昌杰

(甘肃电通电力工程设计咨询有限公司，甘肃 兰州 730050)

0 引 言

超高压输电线路产生的工频电磁污染引起了社会各方面关注，公众对电磁环境问题的关注已成为电网发展的主要制约因素之一。因此，超高压输电线路的电磁环境问题成为线路设计的重要控制因素。目前，国内对超/特高压输电线路电磁环境公众暴露限值控制标准为：工频电场限值4 kV/m，工频磁场限值100 μT，线下耕地、园地、牧草地、养殖水面等场所工频电场限值10 kV/m[1]。随着输电网的大量建设，超高压输电线路工程不可避免地与相对电压等级较低的输电线路产生交叉跨越，而交叉区域电磁环境问题比较复杂，其计算需要建立三维模型。相对于二维场，三维空间的电磁环境计算尚未有成熟的解析方法。目前，电磁环境的计算，主要有应用于微分方程型数学模型的有限元法和应用于积分方程型数学模型的逐次镜像法、模拟电荷法、矩量法等[2-7]。

下面采用有限元法，依托实际工程建立模型，分析超高压交叉输电线路下方工频电磁场的特征，研究影响其强度的相序排列及交叉角等因素；采用屏蔽线降低电磁污染超标的交叉线路场强强度，并对屏蔽线架设位置采用混沌变参数粒子群算法(chaotic particle swarm optimization algorithm with variable parameters，CPSO)进行寻优[3]，为输电线路设计提供指导依据。

1 研究模型

架空输电线路空间工频电磁场受导线对地高度、相间距离、分裂导线结构尺寸、导线布置形式、架空地线以及周围环境等诸多因素影响。电力系统大多采用通用设计塔型，这里以同塔双回750 kV输电线路与单回330 kV输电线路交叉情况为研究对象，建立相应模型，分析线路电磁环境特征以及导线不同相序排列与线路交叉角对工频电磁环境的影响。

交叉输电线路空间布置及相序排列方式如图1所示。所研究模型为：上层750 kV线路采用双回路鼓型铁塔，导线每相为6分裂排列，相邻子导线分裂间距为400 mm，导线采用JL/G1A-400/50钢芯铝绞线，地线采用1×19-13.5-1270-B镀锌钢绞线；下层330 kV线路采用单回路猫头、干字型铁塔，导线每相为双分裂水平排列，分裂间距400 mm，导线采用JL/G1A-300/40钢芯铝绞线；组合相序排列方式共6种。图1中：A1—C1表示750 kV同塔双回线路的1回导线，A2—C2表示 2回导线，D1、D2分别为1、2回线路地线；A3—C3表示330 kV导线，D3为其地线。根据排列方式不同，上层750 kV可排出Ⅰ～Ⅵ六种，下层330 kV可排出1～6六种。

在输电线路三维电磁环境计算中，采用有限元法，将空间网格剖分成许多细小四节点三棱锥(四面体)单元，空间场量的计算可表示为：

(1)

(2)

式中：L为空间三棱锥划分数量；Ui为第i个三棱锥顶点场量；Nei为第i个三棱锥的插值基函数；pi、qi、ri、si、Ve为由三棱锥顶点坐标计算出的系数。

工程用麦克斯韦方程组微分型式可表示为：

∇·D=ρ

(3)

∇·B=0

(4)

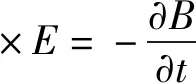
(5)

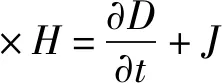
(6)

引入矢量磁位，满足

B=∇×A

(7)

相应有关场量的辅助方程为

D=εE,B=μH,J=σE

(8)

式(3)至式(8)中：E为电场强度；D为电位移；B为磁通密度；H为磁场强度；ρ为电荷密度；ε为介电常数；μ为磁导率；σ为电导率；J为电流密度；t为时间。

以麦克斯韦微分方程组导出用于有限元处理电磁问题的微分方程，计算过程能考虑任意塔形和导线布置，准确计算空间任一点的电磁场强度数值解。

2 交叉线路电磁感应影响要因分析

为考察交叉线路三维电磁环境，在图1所示的空间模型中，以线路下方离地面1.5 m处某平面为考察区域，将目标区域划分成N×N的小方形域，求取每个域的电磁场加权平均值，权重系数应反映每个小区域的重要程度。区域目标函数F可表示为

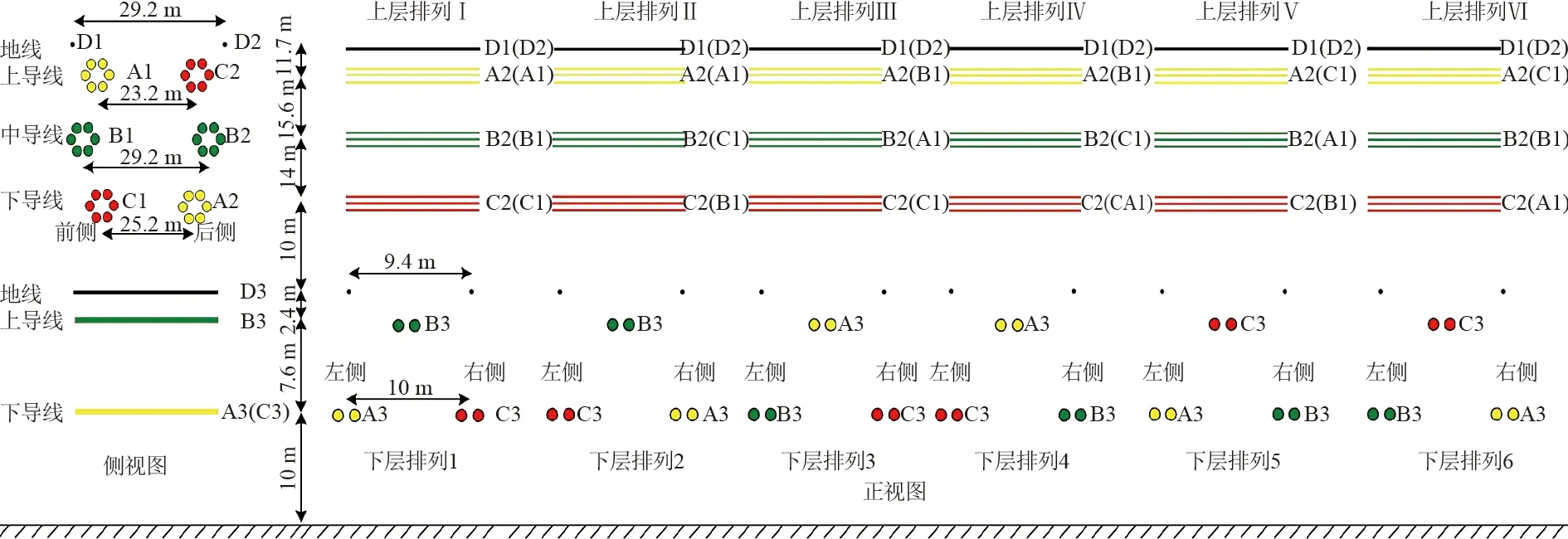
图1 交叉输电线路空间布置方式及相序排列

(9)

式中：Ej为第j个小方域电场强度或磁感应强度；kj为权重系数，∑kj=1，kj∈[0,1]。

2.1 导线相序排列方式对工频电磁场影响

2.1.1 导线相序排列方式对工频电场影响

对图1所示的交叉输电线路相序排列方式进行组合，根据式(9)求线下-40 m～40 m的正方形区域目标值F，线路交叉角取90°，计算结果如表1所示。

表1 不同相序排列方式下区域电场强度 单位：kV/m

图2绘制出了考察区域内电场强度E值。

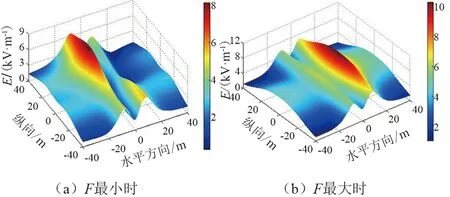
图2 交叉线路下方E值

由表1及图2可以看出，交叉输电线路线下工频电场受上层相序排列方式影响较大。当上层双回线路采取同相序排列时，线下加权平均场强都较大(4.58～6.9 kV/m)；当上层双回线路采取逆相序排列时，线下加权平均场强都较小(4.01～4.88 kV/m)，实际工程中可以采取上层线路逆相序排列方式。

2.1.2 导线相序排列方式对工频磁场影响

与工频电场相似，求解线下区域目标值F，计算结果如表2所示。

表2 不同相序排列方式下区域磁感应强度 单位：μT

图3绘制出了考察区域内磁感应强度B值。

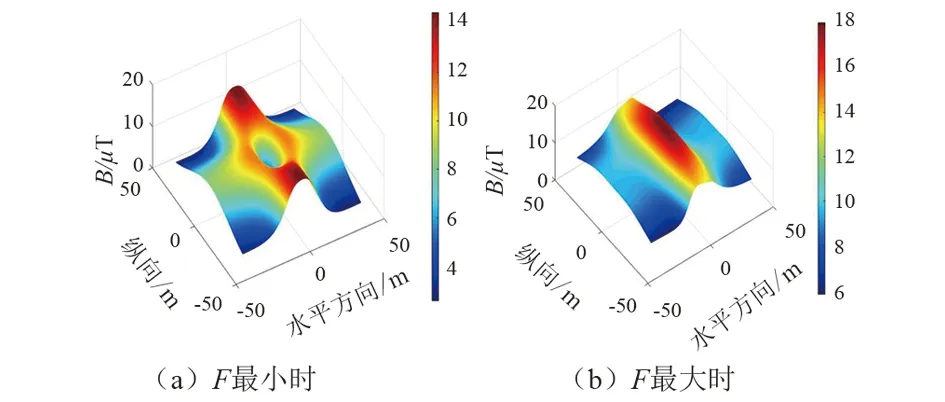
图3 交叉线路下方B值

由表2及图3可以看出，交叉输电线路线下工频磁场受上层相序排列方式影响较大。当上层双回线路采取同相序排列时，线下加权平均场强都较大(13.82～13.91 μT)；当上层双回线路采取逆相序排列时，线下加权平均场强都较小(9.86～13.54 μT)。因此，在实际工程中推荐采取双回路逆相序排列方式。

2.2 线路交叉角对工频电磁场影响

利用2.1所得结果，考察工频电场区域目标值F最小时的相序布置方式，区域目标值F随角度变化情况。目标区域函数值F随线路交叉角变化情况如图4所示。

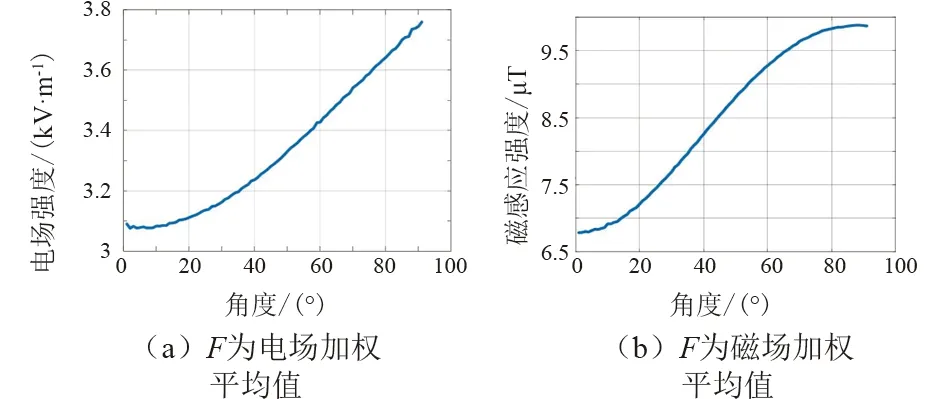
图4 目标区域函数值F随线路交叉角变化情况

由图4可见，随交叉角的增大，目标区域函数值F也相应增大。为提高输电通道本质安全，相关部门要求重要输电线路交跨角不宜小于45°，其线路下方电磁环境如图5所示。

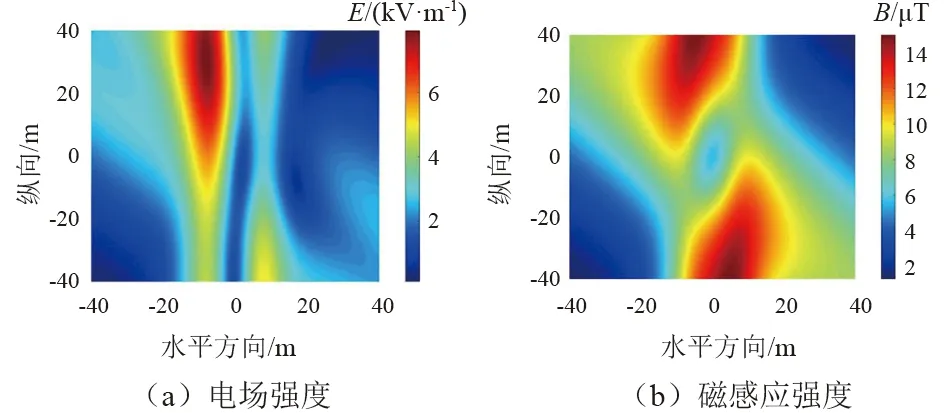
图5 交叉角45°时线路下方电磁环境

3 屏蔽措施

由上述内容可知，交叉线路下方电场强度受相序排列组合及交叉角影响，区域目标值F最小时，线下场强呈现的马鞍面加权平均场强不超标，而沿下层线路方向单侧场强超出标准要求。因此，采用在导线下方架设屏蔽线的方式减小地面工频电场。对屏蔽线架设位置采用CPSO算法进行寻优，实现屏蔽优化设计。

3.1 CPSO算法

标准粒子群优化算法(particle swarm optimization,PSO)的数学描述为：假设在一个d维的目标搜索空间中，有m个代表潜在问题解的粒子组成的一个种群S={X1,X2,…,Xm}，该种群中的第k个元素Xk={xk1,xk2,…，xkd}，表示第k个粒子在d维空间的一个矢量点。用Pkd(pk1,pk2,…,pkd)记录第k个粒子自身搜索到的最优点。而在这个种群中，搜索到的最好值记为g，则Pgd=(Pg1,…,Pgd)。可以用Vk(vk1,vk2,…,vkd)表示第k个粒子的速度。PSO算法采用式(10)实现。

(10)

式中：rand()产生(0,1)之间的随机数；w为惯性权重系数；c1、c2为每个粒子的学习因子；t-1、t为粒子运动时刻。

惯性权重系数取以时间为变量的非线性函数，如式(11)所示。

w(t)=(wmax-wmin)×tan(0.875×

(11)

式中：titer为最大进化代数；t为当前进化数；K为控制因子；wmax、wmin为惯性权重区间上、下限。

PSO算法存在易陷于局部最优、优化计算精度低、后期收敛慢的缺点。故根据混沌运动的随机性、遍历性等特点，采用混沌控制参数变化的粒子群优化算法进行寻优计算。混沌(chaos)是由确定方程得到的非确定随机运动状态，具有随机性、便利性及规律性等特点，能在一定范围内不重复地遍历所有状态。逻辑斯谛方程是一个典型的混沌系统，其公式为

xn+1=μxn(1-xn)

(12)

式中：μ为混沌控制参数;xn为混沌变量，xn∈[0，1]。

CPSO算法具体的流程描述如图6所示。

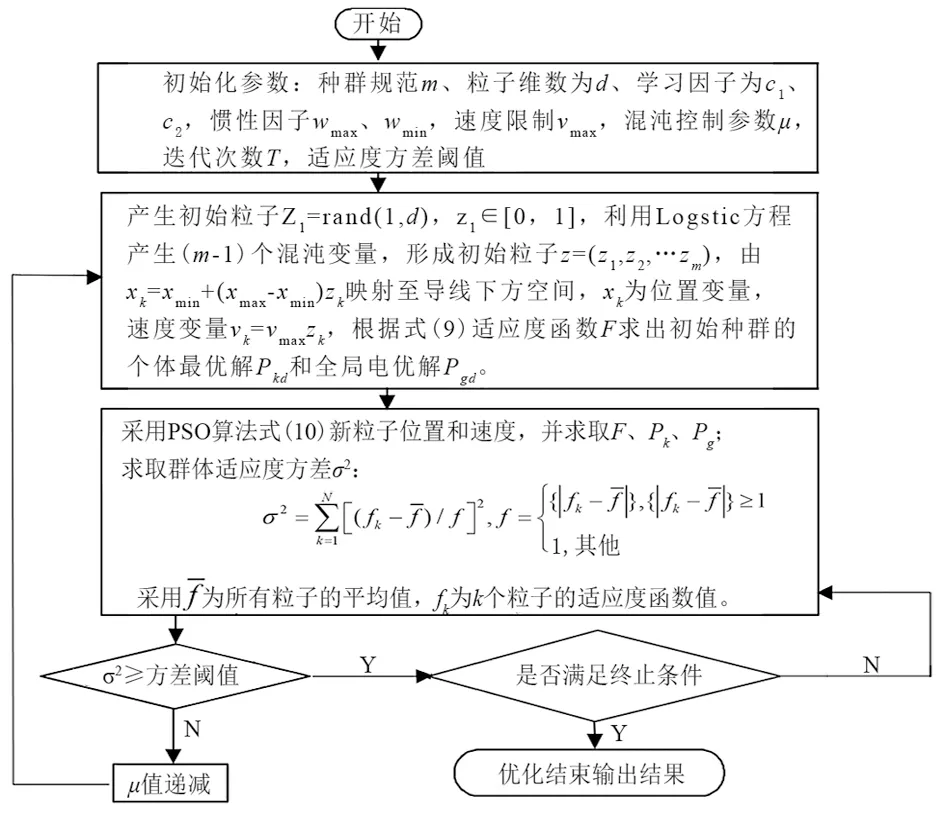
图6 CPSO算法流程

由于混沌变量的遍历性和随机性有助于增强种群的搜索能力，在算法运行过程中，根据种群的收敛情况，动态地减小式(12)中混沌控制参数μ，降低混沌运动对种群结构的破坏，摆脱陷入局部最优的困境。

3.2 CPSO算法优化屏蔽仿真实验

以区域目标函数F作为CPSO算法的适应度函数，并沿下层线路方向架设屏蔽线，屏蔽线高度lh在[0，20]区间取值，水平位置lp在[-30，30]区间取值。分别对架设单根及两根屏蔽线的位置进行寻优，得到适应度函数收敛曲线，如图7所示。由图可见，混沌变参数粒子群优化算法在保证算法能摆脱局部最优的基础上，明显提高了收敛性能。

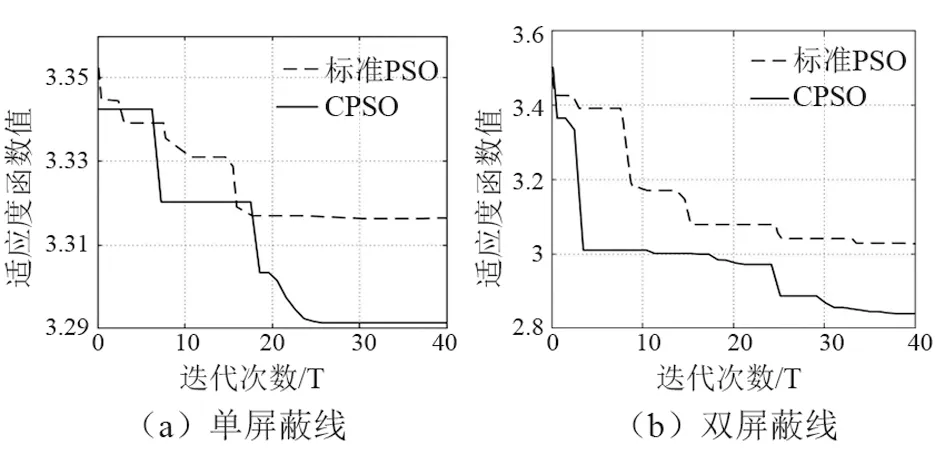
图7 适应度函数收敛曲线

对屏蔽线架设位置通过CPSO算法寻优，得到的架设位置为：单屏蔽线lh=2.32 m、lp=-8.49 m；双屏蔽线lh1=3.12 m、lp1=7.80 m、lh2=2.32 m、lp2=-8.50 m。架设屏蔽线后，考察-40 m～40 m正方形区域内，交叉线路下方场强如图8所示。

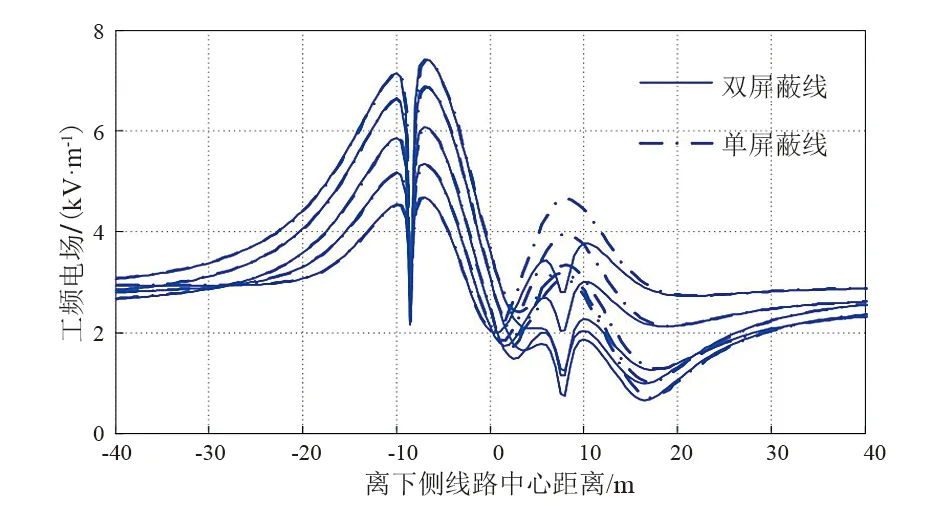
图8 架设屏蔽线后线路下方不同横断面E值

架设屏蔽线后交叉线路下方E值如图9所示。可以看出，CPSO寻优位置基本在畸变的马鞍面电场峰值附近，架设单屏蔽线可以将加权场强均值从3.91 kV/m降至3.29 kV/m，而架设双屏蔽线降可至2.85 kV/m，场强峰值位置处降低较明显，屏蔽效果良好。

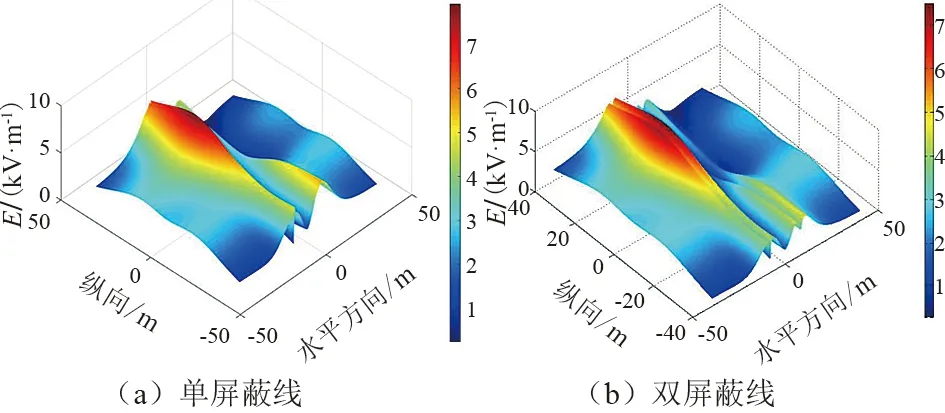
图9 架设屏蔽线后交叉线路下方E值

4 结 论

上面采用有限元法，通过一系列仿真实验，在构造的区域目标函数基础上，研究线路相序布置和交叉角对空间电磁环境的影响，并给出可用于工程的相序排列方式及交叉角建议：为简化设计难度，在满足设计要求时，上层双回路宜采用逆相序布置，交叉角可适当减小，以降低空间电磁污染。

采用架设屏蔽线的方式改善地面电磁环境，并引入混沌变参数粒子群算法，对屏蔽线架设位置进行目标寻优，寻优过程中，动态减小混沌控制参数值，使算法在迭代过程中逐步减弱混沌运动，进而在保留混沌粒子群优化算法优点的基础上，又增添了粒子群体的多样性，实现快速跳出局部最优点，寻找全局最优解。通过CPSO算法对屏蔽线架设位置寻优，实现区域电磁环境屏蔽效果最优。