一种适用于深部煤岩的甲烷损失气量计算方法

宋利红 杨 宇 徐启林 张 昊 吴 翔

1.成都理工大学能源学院 2.阿德莱德大学澳大利亚石油学院 3.中联煤层气有限责任公司

0 引言

研究甲烷在煤岩中的扩散规律，对于预测煤与甲烷突出危险性等都具有重要现实意义[1]。而煤层含气量的测定准确性程度是一个亟待解决的基础科学问题[2]。含气量由扩散（损失）气量、解吸气量及残余气量三部分组成，后两者可在解吸罐中测量，于是损失气量就成了确定含气量的关键[3]。国内外对甲烷扩散进行了大量实验和理论模型研究。在国内外煤岩甲烷扩散理论模型中，多以定浓度外边界条件下的甲烷扩散为假设条件，代表性的工作有：①张飞燕及韩颖[4-5]等人研究了定扩散系数Fick扩散，将煤屑看成一种理想吸附剂，然后假设扩散系数为定值。②李建功[6]得出：随解吸时间延长，不同形状煤屑内部甲烷有效扩散逐渐近似于球形。而考虑外边界浓度变化的模型较少，且相比于Freundlich吸附方程，应用Langmuir方程，需要应用数值求解累积的甲烷逸散量[7-8]。

目前，对于非密闭取心工艺的测试结果，通常采用USBM法计算损失气量。在深部煤层取样过程中，当煤岩从储层提至井口附近浅表地层段时，煤岩心的外表压力可从几、几十兆帕降为大气压，压力变化导致煤岩外表面浓度的变化。而USBM法中将煤岩外表面浓度视为0的假设条件与实际有较大差别。当煤层取样深度较小时，USBM法的计算结果较为准确[9]；但对于深部煤层气井，由于甲烷初期解吸并非呈线性规律或USBM法中与时间平方根的线性规律，计算误差也将随深度而增大。因此，对损失气量的计算进行改进，对准确评价深部煤层含气量具有重要意义。

综上所述，基于前人成果，本文将井筒与解吸罐情景结合起来综合研究煤岩中甲烷扩散，构建了变浓度外边界条件的解吸扩散数学模型，并将其计算结果与前人的研究对比。在此基础上，采用最优化方法计算煤岩在井筒提升过程的损失气量，与常用USBM法对比分析计算结果。

1 在现场取样和测试过程中的甲烷扩散特征

1.1 煤岩心在提升过程的甲烷扩散特征分析

如图1所示，在取心后向上提的过程中，煤岩外表面压力等于相应位置的钻井液静液柱压力。

图1 直井井筒中煤岩提升过程示意图[10]

在煤岩提升过程中，假设钻遇煤岩层时刻为t1、开始取样时刻t2，其他重要的时间节点如图2所示，包括：开始起钻时刻t3、煤岩提至井深一半时刻t4、提出井口时刻t5、装罐结束时刻t6。在取心后期，由于钻铤和取心器具卸扣时间较长，所以，煤岩提升位置与上提时间是非线性关系。

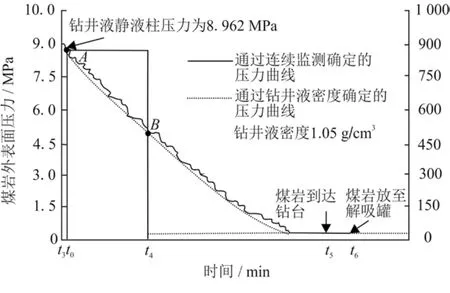
图2 煤岩样品提升过程中外表面压力变化示意图

假定煤岩储层被气体饱和。在岩心上提到某一深度时，钻井液的静液柱压力等于原始地层压力，煤岩中的甲烷就会发生解吸扩散，该深度对应的时刻称为零时刻t0。在USBM法中，零时刻定义为煤样被提升到离井口一半深度处的时刻。在A点时（图2），钻井液的静液柱压力等于原始地层压力，而USBM法中设置的零时刻点为B点。因此，当煤层越深，A与B两点间的距离越大，USBM法计算偏差也越大。

1.2 解吸罐中甲烷扩散特征分析

煤作为一种复杂孔裂隙体，甲烷在煤体中的扩散存在5种类型（菲克、诺森、过渡型、表面和晶体扩散）。目前国内研究煤屑中甲烷扩散理论，大多以菲克扩散模型为基础，而对其他4种类型的扩散规律研究较少[11]。研究中所涉及的煤屑甲烷扩散实质为甲烷气体分子从煤固体表面脱附的过程，因此煤屑甲烷扩散受浓度差影响。在甲烷开始扩散前，煤屑内部各点的甲烷浓度为吸附平衡时的浓度，甲烷球向流动场长度不大于煤屑半径时，煤屑中心的甲烷浓度为吸附平衡时的浓度。

在煤矿井下实际工程中，大多由定容容器测定气体压力变化来算煤屑甲烷扩散量。这从数学物理角度来分析，定容条件下的煤屑甲烷扩散，其数学模型的外边界浓度应为随时间变化的函数，而非定值。在本文中，假定煤屑为球形进行甲烷扩散规律研究。

2 井筒与解吸罐中的甲烷扩散数学模型

2.1 甲烷扩散模型的构建

煤样中的甲烷扩散属于气体分子不规则热运动与孔隙管道表面碰撞的综合作用结果，可利用热传导相关的数学物理方程对煤屑甲烷扩散问题进行理论分析。文中基于Fick第二扩散定律，结合煤储层特征、甲烷赋存状态与扩散运移规律，对井筒和解吸罐中甲烷解吸扩散模型做出如下假设：

（1）煤样为球形颗粒的集合；

（2）煤屑为均质、各向同性多孔介质体；

（3）甲烷扩散流动遵从质量守恒定律和连续性原理；

（4）忽略煤岩在提升过程中温度的变化。

（5）假设煤层被气体所饱和，可用Freundlich吸附方程表示甲烷浓度与压力的关系[12]。

（6）忽略煤岩提升到井口至转入解吸罐密封前的地面暴露时间。

（7）假设煤岩在井筒提升过程中，其提升高度h与时间t近似成二次多项式关系。且将提升过程中煤岩所在深度的钻井液柱静液柱压力等于原始地层压力时的时刻定义为甲烷解吸扩散的零时间t0。

在不考虑瞬间暴露解吸过程对甲烷扩散影响下，不同坐标系甲烷扩散数学模型为:

式中C为煤岩中甲烷的浓度，g/cm3；D为扩散系数，cm2/h；t为时间，h；r为甲烷气体到煤屑中心的距离，cm；当S=0，1，2时，表示煤屑形状为板状、柱状与球体时的甲烷扩散。

本文研究的是针对s=2时的球形煤屑甲烷扩散。即式（1）简化得[13]：

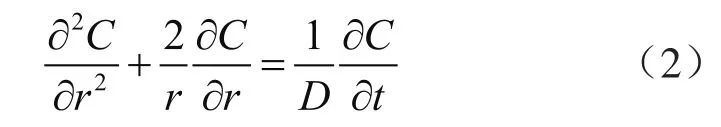
基于模型假设条件，甲烷扩散方程的初始条件和边界条件如下。

①初始条件

式中Ci为煤岩中甲烷的初始浓度，g/cm3；R为煤岩半径，cm。

②内边界条件

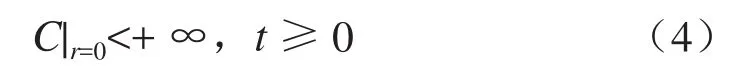
③外边界条件

由如图1和图2所示，在岩心提升过程中，岩心提升距离h与时间t之间可以近似为二项式关系：

式中h为岩心在井筒中提升的高度，m；Z0为钻井液的静液柱压力等于原始地层压力时的深度，m；t为时间（从零时间t0开始计），h；m、n为系数。

井筒中，钻井液压力（p）与煤岩上提深度（Z）满足静压公式：

另外，在井筒中，岩心外表面压力等于同深度处泥浆静液柱压力。由式（5）、（6）可得，岩心外表面压力（p）为：

式中a，b为系数；pi为原始煤层压力，MPa。

甲烷浓度可用Freundlich等温吸附方程来描述，即Cb(t)=knpm，则

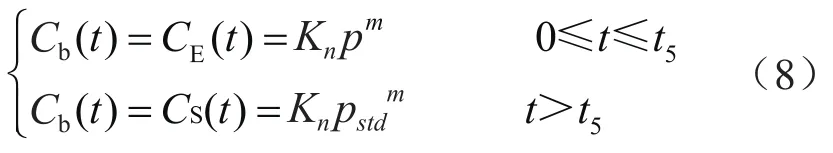
式中CE(t)为井筒中煤岩甲烷在t时间的浓度，g/cm3；CS(t)为解吸罐中煤岩甲烷在t时间的浓度，g/cm3；pstd为大气压力，即0.1 MPa；t5为煤岩提至井口的时间（从零时间t0开始计时），h；Kn和m是可根据等温吸附测试得到且与吸附剂、吸附质的种类及性质有关的等温吸附常数，Kn一般大于0，m是小于1的正数。

综上所述，极坐标系下煤岩在井筒与解吸罐中甲烷扩散数学模型为：

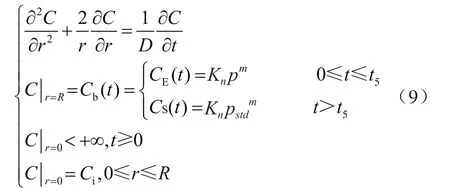
2.2 甲烷扩散模型的求解

Carslaw[14]等认为，扩散运动类似于热传导运动，于是，对于方程（1）将采用数理方程的求解方法进行求其解析解。

2.3 定浓度外边界的模型求解

3 甲烷扩散规律与扩散气量分析

3.1 计算思路

在煤岩含气量的现场测试中，煤岩含气量是残余气量、解吸罐中的解吸气量和井筒中扩散（损失）气量之和。由于现场一般不计量井筒中的损失气量，可根据解吸罐中的解吸气量推测井筒中损失气量。图3为最优化方法求井筒损失气量的基本流程。

图3 拟合求损失气量流程图

3.2 解吸罐中甲烷扩散气量计算

据调研知，解吸罐中煤屑甲烷扩散规律的表征有两种方式：①用累计甲烷扩散气量表示；②用甲烷扩散速度表示。下面将分析研究由累计甲烷扩散气量来表征其扩散规律的情况。

图4是结合某实际煤层气藏X样品已有数据基础上，采用Matlab软件编程进行三次样条插值的结果。其中取B=6.579 7 10-51/h，煤岩半径R=7.3 cm，甲烷初始浓度Ci=0.018 g/cm3，甲烷浓度Cb（t）=0.007 7（0.348t2-3.423t+8.67）0.39。

图4 煤屑甲烷扩散规律模拟结果图（解吸罐中）

本研究条件下得到的扩散时间与扩散率的曲线关系与杨其銮等人采用塞文斯特（p.G.Sevenster）提供的数据范围拟合的结果相似，都是在B=6.579 7 10-6～6.579 7 10-3范围，本文具体取值为B=6.579 7 10-51/h。

3.3 煤岩心在提升过程的甲烷扩散气量计算

以某煤层气藏的X样品为例：煤岩质量2 866 g，密度为1.75 g/cm3，扩散系数为3.55 10-4cm2/h，煤岩折算成球形半径约为7.3 cm。取心深度为880 m，原始地层压力8.67 MPa，地层温度45 ℃。钻井液密度为1.05 g/cm3，由测试得解吸气含量与残余气含量之和为4.87 cm3/g。在深度838 m处钻井液的静液柱压力与原始地层压力相等。因此，将煤岩被提至838 m处的时刻设为零时间。从零时间至煤岩被提至井口，共耗时5 h，即：t5=5 h。因煤岩在地面暴露时间较短，于是该时间不计入扩散量计算。

由前述可知，煤屑吸附甲烷的压力与时间近似成二项式关系，其拟合结果如图5所示。

图5 压力与时间的拟合关系曲线

可知，对于煤屑吸附甲烷压力与时间关系式p=at2+bt+pi中，a=0.387，b=-3.68，pi=9.28 MPa， 即p=0.387t2-3.68t+9.28。

甲烷浓度可以用Freundlich等温吸附方程来描述，图6是用Freundlich等温吸附方程来拟合不同压力下的煤屑甲烷浓度，具体结果如下。

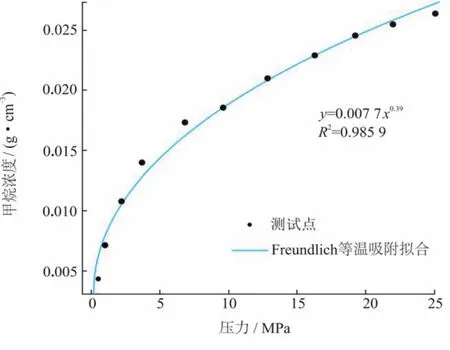
图6 煤屑中甲烷浓度与压力关系图

由图6可知，甲烷浓度与压力之间的关系为：C=0.007 7p0.39。即 ：K=0.0077，m=0.39。

煤岩在解吸罐中完整解吸数据如图7所示。取其解吸罐内前3 h的解吸数据进行损失气量拟合。

图7 解吸罐中煤样的累计甲烷解吸时间与解吸量关系图

依最优化算法，采用式（36）对解吸罐中解吸气量进行拟合，得Ci=0.051 g/cm3，拟合效果如图8所示，其相关系数为0.997，精度较高。

图8 实测解吸气量拟合效果图

将拟合的煤岩初始含气浓度Ci代入式（30），得到煤岩在井筒提升过程中损失气量为2 951 cm3。

图9为用USBM法拟合得到的损失气量，值为2 712 cm3，得知该结果小于本文扩散模型的计算结果。

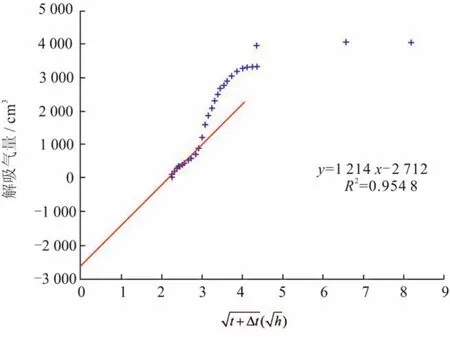
图9 USBM法计算损失气量图（∆t为煤岩提升时间）

图10为USBM法与本文二项式计算模型的损失气量计算结果对比。

图10 不同方法下X样品的损失气量图

由于煤样在钻井液静液柱压力与原始储层压力相等时就开始解吸，但USBM 法假定解吸的零时间t0为样品被提升到离井口一半深度时的时间，因此USBM 法采用的损失气时间小于实际的损失气时间（损失气时间越长，得到的损失气量越大）。另外，USBM法采取的直线外推法是根据在大气压力下收集的解吸速率和解吸气量来计算损失气量的，即USBM 法试图通过人为地推迟零时间点来减少实际的损失气时间，这种方法一般会造成计算的损失气量偏低。

4 结论

基于Fick扩散定律建立了煤岩在井筒与解吸罐中外边界浓度变化的甲烷扩散模型，并通过数理方程求解方法求得了其解析解。在此基础上，与前人构建的解吸罐中定边界浓度扩散模型进行对比，得出本文所建扩散模型更具有普适性，综合性强的特点。

依据所建扩散模型，用最优化方法对解吸罐中的实测解吸数据进行拟合，进而可推测出井筒中损失气量。

由于本文建立的扩散模型考虑了煤岩提升过程中岩心外表面压力随时间变化的非线性特征，这可以更加准确地表征煤层气藏中甲烷在取心提升过程中的扩散规律。因此，与USBM法相比，本文模型计算的井筒中甲烷损失气量更准确可靠。