含锯齿状结构面的岩质边坡稳定性拟动力分析

2022-07-01孙树林高诗钦龚郴彬

河北工程大学学报(自然科学版) 2022年2期

潘浩，孙树林，高诗钦，龚郴彬

(河海大学地球科学与工程学院，江苏南京 211100)

边坡稳定性是建筑、交通、水利水电以及矿产开发等各项工程中最常遇到的地质灾害之一，每年不仅给我国带来巨大的经济损失，也严重危害了人民的生命财产安全，所以研究边坡稳定性具有非常重要的经济和社会意义。

结构面的性质对岩体稳定性有着非常重要的影响，其剪切力学特性是工程地质领域的重要研究内容之一。李海波[1]通过对混凝土试件直剪发现锯齿状结构面的峰值剪切强度随着法向应力、初始起伏角以及岩壁强度的增大而增大。沈明荣等[2]研究了规则锯齿型结构面剪切强度及变形等力学特性。Homand等[3]分析了剪切前后节理表面面积的衰减变形规律，定量描述了低法向应力循环剪切条件下齿状节理面磨损随法向应力增强的特性。Seidel等[4]通过加工的规则锯齿状节理面直剪试验及能量分析，发现在有效法向应力增大的情况下剪胀角发生明显减少。这些试验为研究含有锯齿状结构面的岩质边坡稳定性提供了新的角度。近几十年来，世界各国的学者针对边坡安全提出了很多分析方法，如拟静力法[5]、拟动力法[6]、数值模拟分析法[7]、Newmark滑块位移分析法[8]以及概率分析法[9]等。其中拟动力法是利用正弦波来模拟土体中地震波的传播情况，土体竖直方向上受到的地震力变化则通过放大系数进行计算[10]。Nimbalkar 等[11]通过拟动力法分析了加筋土挡墙曲线破裂面的边坡稳定性。Ghosh[12]通过拟动力法分析了倾斜挡土墙的土压力分布情况。阮晓波等[13]基于拟动力法研究了挡土墙的主动土压力，得到了地震条件下主动土压力的计算公式以及临界破裂角的解析解。拟动力法得到的结果展现了地震力随时间的变化以及土体中地震波的传播情况，更好地反映了边坡的动态稳定性。

综上所述，本文使用改进拟动力法对具有锯齿状结构面的岩体进行稳定性分析，综合考虑了地下水作用、坡顶荷载、地震作用以及锚固效应等一系列条件的影响，推导了锯齿状结构面岩体的安全系数，分析了滑面倾角、锚固效应、地震作用、起伏角等相关因素对锯齿状结构面岩体边坡稳定性的影响。

1 改进的拟动力法基本理论简介

Bellezza等[14]基于岩质材料为Kelvin-Voigt粘弹性介质对传统拟动力法进行了改进，但他提出的这种改进方法主要是针对边坡高度对地震加速度的影响，而对岩体的刚度和阻尼、边坡结构的刚度和几何形状、岩体深度等影响地震加速度的因素研究不足。为了更好地展现各种因素综合作用产生的效应，进而引入了放大系数f。通过Bellezza的研究可以知道考虑放大系数后，任意时间t下岩体任意深度z处地震作用引起的水平ah(z,t)和垂直av(z,t)加速度分别为：

SsSsz)cos(ωt)+(SsCsz-CsSsz)sin(ωt)]

(1)

SpSpz)cos(ωt)+(SpCpz-CpSpz)sin(ωt)]

(2)

式中：

Cs=cos(ys1)cosh(ys2)

Ss=-sin(ys1)sinh(ys2)

Cp=cos(yp1)cosh(yp2)

Sp=-sin(yp1)sinh(yp2)

Vs=(G/ρ)1/2

VP=[2G(1-υ)/ρ(1-2υ)]1/2

其中：υ为泊松比；ρ为岩体密度；D为岩石的阻尼比；G为岩体的剪切模量；ω=2π/T：ω为角速度，T为震动周期；H为边坡高度；f为地震放大系数；kh为水平地震系数；kv为竖向地震系数。

由图1可知任意深度z处薄层单元体的质量为：

(3)

所以边坡所受的水平地震力Qh和竖向地震力Qv大小分别为：

(4)

(5)

将ah(z,t)、av(z,t)以及m(z)代入，则：

SsSsz)cos(ωt)+(SsCsz-CsSsz)sin(ωt)]×

(6)

SpSpz)cos(ωt)+(SpCpz-CpSpz)sin(ωt)]×

(7)

2 计算公式推导

2.1 计算模型建立

根据Hoek和Bray[15]给出的典型岩石边坡作为计算模型，主要考虑锚固力、地震力、坡顶荷载、结构面作用以及静水压力对边坡稳定性的影响，同时为了计算的需要以及地震力的传播进行如下假设：岩质边坡为Kelvin-Voigt材料；边坡的剪切模量是不变的；岩质边坡是刚性的，其破坏方式为平面滑动破坏。

坡体的几何要素如图1所示：坡脚为∂，坡高为H，张裂缝深度为h，在自身重力G、地震力、坡顶荷载q以及静水压力的作用下，形成了滑动体ABCO，其中滑动面OC与水平面的夹角为θ，锚索与水平面的夹角为α，T1为锚索预设拉力值。

图1 加锚边坡平面滑动受力分析Fig.1 Plane sliding force analysis of anchoring slope

2.2 推导安全系数计算公式

黄达[16]在Mhor-Coulomb屈服准则的基础上，为了使抗剪强度公式一方面反映锯齿状结构面的啃断效应，另一方面反映其爬坡效应，引入了结构面起伏角，提出了锯齿状结构面的剪切强度公式：

τ=σntan(φb+0.155β)+0.012βCb

(8)

式中：τ为峰值剪切强度；φb为平滑结构面的基本摩擦角；σn为法向应力；β为结构面起伏角；Cb为完整岩石的黏聚力。

由图一中的几何关系可得：

(9)

(10)

所以滑块ABCO的重力为：

(11)

地下水对边坡BC和OC边的作用力分别为W1和W2：

(12)

(13)

式中：γw为水的重度。

所以可以计算得到OC滑动面上的正应力σn为：

(14)

锯齿状滑动面上的剪应力为：

τ=σntan(φb+0.155β)+0.012βCb

(15)

进而可以得到滑动面上抗滑力Fr为：

Fr=τL=[(G+ql+Qv)cosθ-(W1+Qh)×

sinθ-W2+T1sin(α+θ)]tan(φb+

0.155β)+0.012βCbL

(16)

坡体的下滑力Fi为:

Fi=(G+ql+Qv)sinθ+(W1+Qh)cosθ-

T1cos(α+θ)

(17)

然后利用极限平衡分析法对坡体进行分析，可得到安全系数Fs为:

[(G+ql+Qv)cosθ-(W1+Qh)sinθ-W2]/

[(G+ql+Qv)sinθ+(W1+Qh)cosθ-T1cos(α+θ)]+

[T1sin(α+θ)]tan(φb+0.155β)+0.012βCbL]/

[(G+ql+Qv)sinθ+(W1+Qh)cosθ-T1cos(α+θ)]

(18)

3 算例及参数敏感性分析

如图1岩质边坡经典模型所示，基本参数如下：坡高H=10 m、岩石阻尼比D=0.3、黏聚力Cb=12 kPa、地震周期T=0.3 s、坡顶荷载q=60 kN/m、横波波速Vs=2 900 m/s、纵波波速Vp=3 900 m/s、放大系数f=1.2、水平地震加速度系数kh=0.3、竖向地震加速度系数kv=0.15(Qv竖向地震力方向向下为正，向上为负)、锚固力T1=400 kN、锚固角α=20°、水位深度hw=1 m、起伏角β=25°、边坡倾角∂=60°、滑动面倾角θ=20°、内摩擦角φb为30°、岩体重度γ为26 kN/m3，计算出Fs=1.268。研究参数变化时取值如表1所示。

表1 计算参数Tab.1 Calculation parameters

利用Matlab软件根据公式(18)计算出相应的安全系数Fs，其结果如图2—图13所示。

3.1 静态稳定性参数分析

由图2可以看出：其他条件一定时，边坡安全系数随着水位深度的增加而逐渐下降，呈近似线性关系，曲线斜率随着水位深度增加略有增加，水位深度从0增加到2 m时，安全系数Fs从1.31降低到1.21，减小了7.6%，因此在边坡施工过程中要做好排水工作，尽量减小地下水的影响。从图3可以看出：边坡安全系数随着边坡倾角的增大而降低，曲线斜率逐渐减小，说明Fs随着边坡倾角的增大下降速率逐渐减缓。当边坡倾角从40°增加到80°时，安全系数Fs从1.37降到1.23，减小了10.2%，当边坡倾角达到65°后，其对安全系数的影响的比较轻微。

图2 水位深度hw对边坡安全系数的影响Fig.2 Influence of water level depth hwon safety

图3 边坡倾角∂对边坡安全系数的影响Fig.3 Influence of slope angle ∂ on safety factor factor of slope of slope

由图4、图5可以看出：岩体起伏角与安全系数呈近似直线关系，Fs随着β的增大而增大。图4中：随着锚固力逐渐增加，直线的斜率逐渐增大。当T1=0时，随着β从10°增大到45°，Fs从0.932增加到1.143，增加了0.211；在T1=200、400、600和800 kN情况下，Fs分别增加了0.236、0.263、0.295以及0.333。说明随着锚固力增大，起伏角β对边坡稳定性的影响也在增大。由图5可知，随着锚固角的增大，直线的斜率略微减小。随着β从10°增大到45°，在α=10°、20°、30°、40°、50°、60°、70°以及80°的情况下、Fs分别增加了0.264、0.263、0.26、0.255、0.25、0.243、0.236以及0.229。锚固后起伏角对安全系数的影响有所增加，但这种影响随着锚固角的增大而逐渐减小。锚固前后，Fs的变化率随着起伏角β的增大变化不大，其范围在22.6%～22.8%之间。

图4 不同锚固力T1下β对边坡安全系数的影响Fig.4 Influence of β on safety factor of slope under

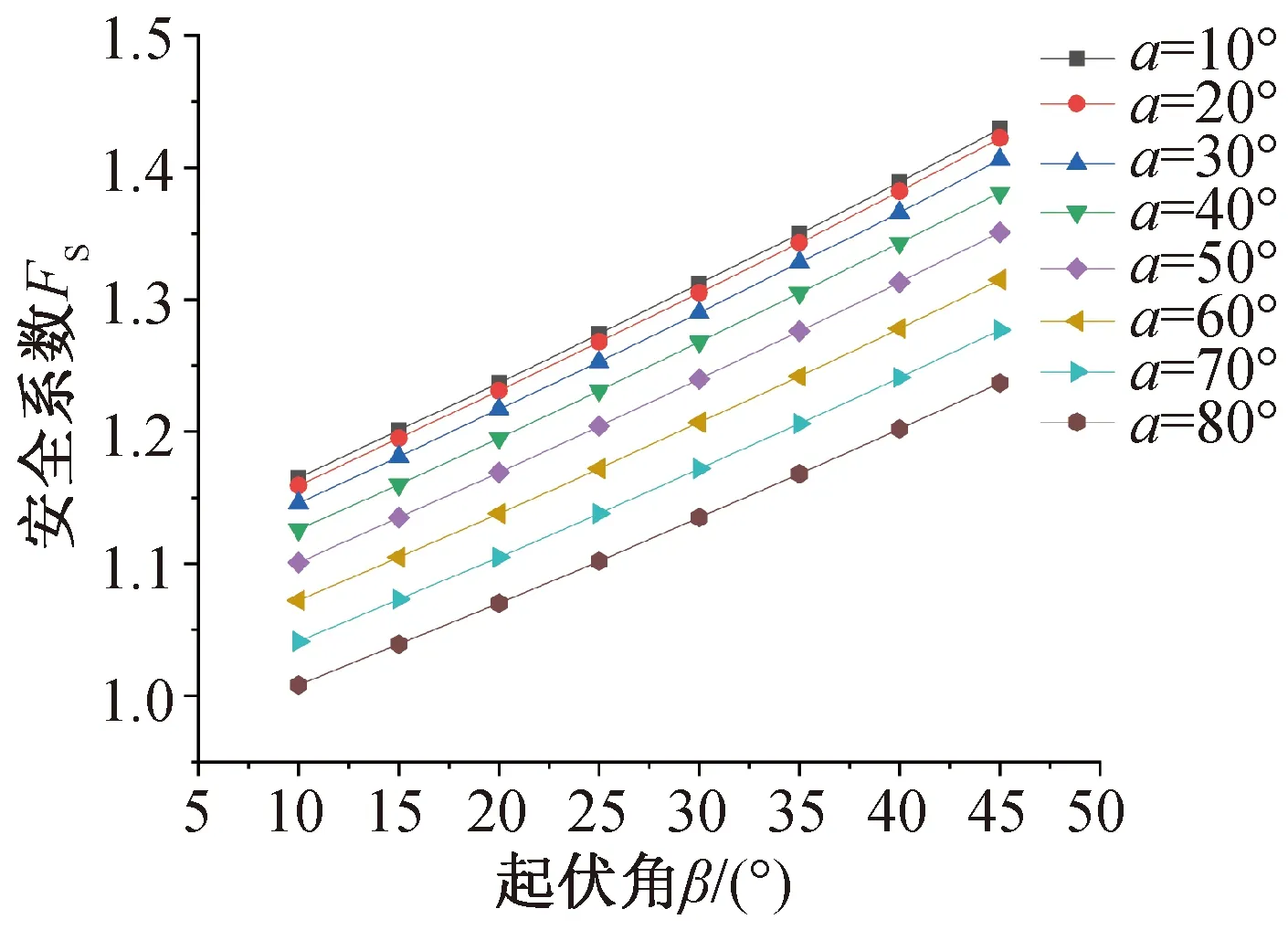
图5 不同锚固角α下β对边坡安全系数的影响Fig.5 Influence of β on safety factor of slope at different different anchorage force T1 anchoring angle α

由图6可以看出：当内摩擦角从20°增加到40°时，Fs从0.84增加到了1.82，增加了116.7%，曲线斜率越来越大，说明随着内摩擦角的增大，其对边坡稳定性的影响越来越强烈。对比其他因素，内摩擦角对Fs的影响远远大于其他因素对边坡稳定性的影响，在边坡抗滑稳定性分析中起着至关重要的作用。由图7可知：安全系数Fs随着滑动面倾角的增大逐渐减小，并且曲线的斜率越来越小，说明随着滑动面倾角的增加安全系数下降的速率越来越慢。当θ从16°增加到30°时，Fs从1.43下降到1.00，降低了30.1%。由图8可知：边坡安全系数随着土体重度的增大而减小，呈近似线性关系，当土体重度从22 kN/m3增加到29 kN/m3时，Fs从1.33降低到1.23，降低了7.5%，说明土体重度对安全系数的影响相对有限，安全系数在不同土体重度下的变化相对较小。

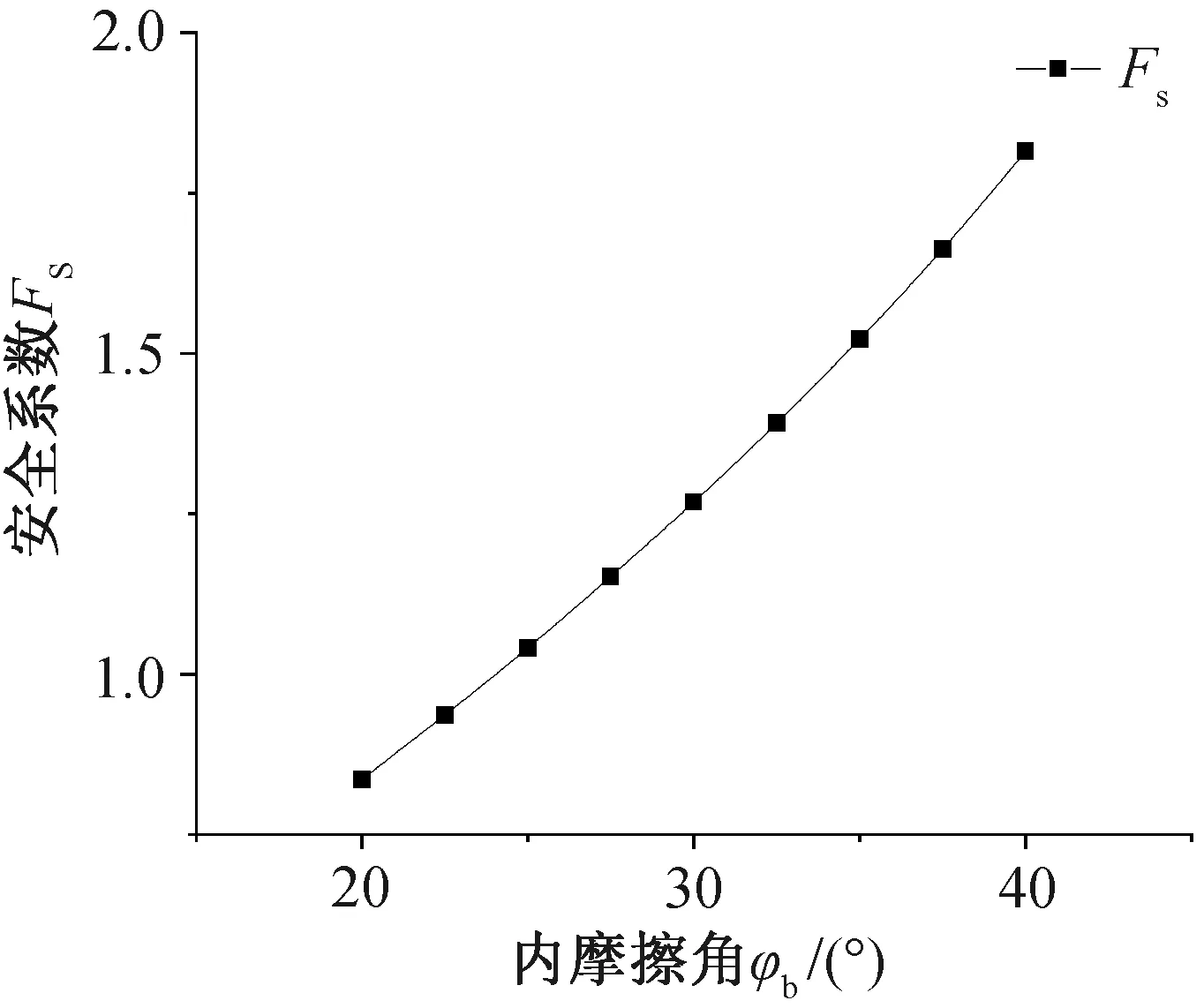
图6 内摩擦角φb对边坡安全系数的影响Fig.6 Influence of internal friction angle φbon

图7 滑动面倾角θ对边坡安全系数的影响Fig.7 Influence of dip angle θ of sliding planesafety factor of slope on safety factor of slope

图8 土体重度γ对边坡安全系数的影响Fig.8 Influence of soil weight γ on safety factor of slope

3.2 锚固参数分析

由图9可知：当保持锚固角不变时，边坡安全系数随着锚固力增大而增大，且速率越来越快。当锚固力从0增加到800 kN时，在锚固角α=10°、15°、20°、25°、30°的情况下，安全系数Fs分别增加了60.8%、59.8%、57.8%、54.9%以及52.0%，说明增加锚固力能很好地提升岩质边坡的抗滑稳定性。同时可以看出随着锚固角的增大，安全系数有所下降，但下降幅度较小，说明当锚固角α较小时，锚固力T1对边坡安全系数的影响远大于锚固角的影响。由图10可知：当保持锚固力大小不变时，边坡安全系数随着锚固角的增大而减小，下降速率逐渐增大。在T1=200、400、600、800 kN情况下，当锚固角从0°增加到80°时，锚固力越大，安全系数减小的越快，当α=80°时，安全系数分别降低了6.1%、13.4%、20%、27.7%，四种锚固力在α=80°的情况下安全系数相差不大，说明当锚固角大到一定程度时，锚固角成了影响边坡安全系数的主要因素，而锚固力的大小影响相对较小。

图9 锚固力T1对边坡安全系数的影响Fig.9 Influence of anchoring force T1 on safety factor of slope

图10 锚固角α对边坡安全系数的影响Fig.10 Influence of anchorage angle α on safety factor of slope

3.3 地震作用的影响

由图11可知：安全系数Fs随着放大系数f的增大而减小，随着f从1.0增加到1.8，在水平地震加速度系数kh=0.1、0.2、0.3和0.4的情况下，Fs分别降低了9.8%、15.1%、19.4%和21.7%，说明地震作用放大效应对边坡的稳定性有着明显影响，并且随着kh的增加，放大系数f对安全系数Fs的影响也在增加。由图12可知：安全系数Fs随着kh的增大而减小，在放大系数f=1.0、1.2、1.4、1.6和1.8的情况下，当kh从0增加到0.4时，Fs分别降低了52.9%、55.6%、58.4%、60.7%以及62.7%，虽然随着f的增大，kh对边坡稳定性的影响有所提升，但是相比于放大系数f的影响，Fs的变化在水平地震加速度系数kh的作用下更为显著。由图13可知：安全系数Fs随着kv的增大而减小，在放大系数f=1.0、1.2、1.4、1.6和1.8的情况下，当kv从-0.2增加到0.2时，Fs分别降低了8.8%、10.9%、13.1%、17.2%以及20.7%，竖向地震加速度系数kv对Fs的影响远远小于水平地震加速度系数kh的影响。

图11 放大系数 f对边坡安全系数的影响Fig.11 Influence of amplification factor f on slope safety factor

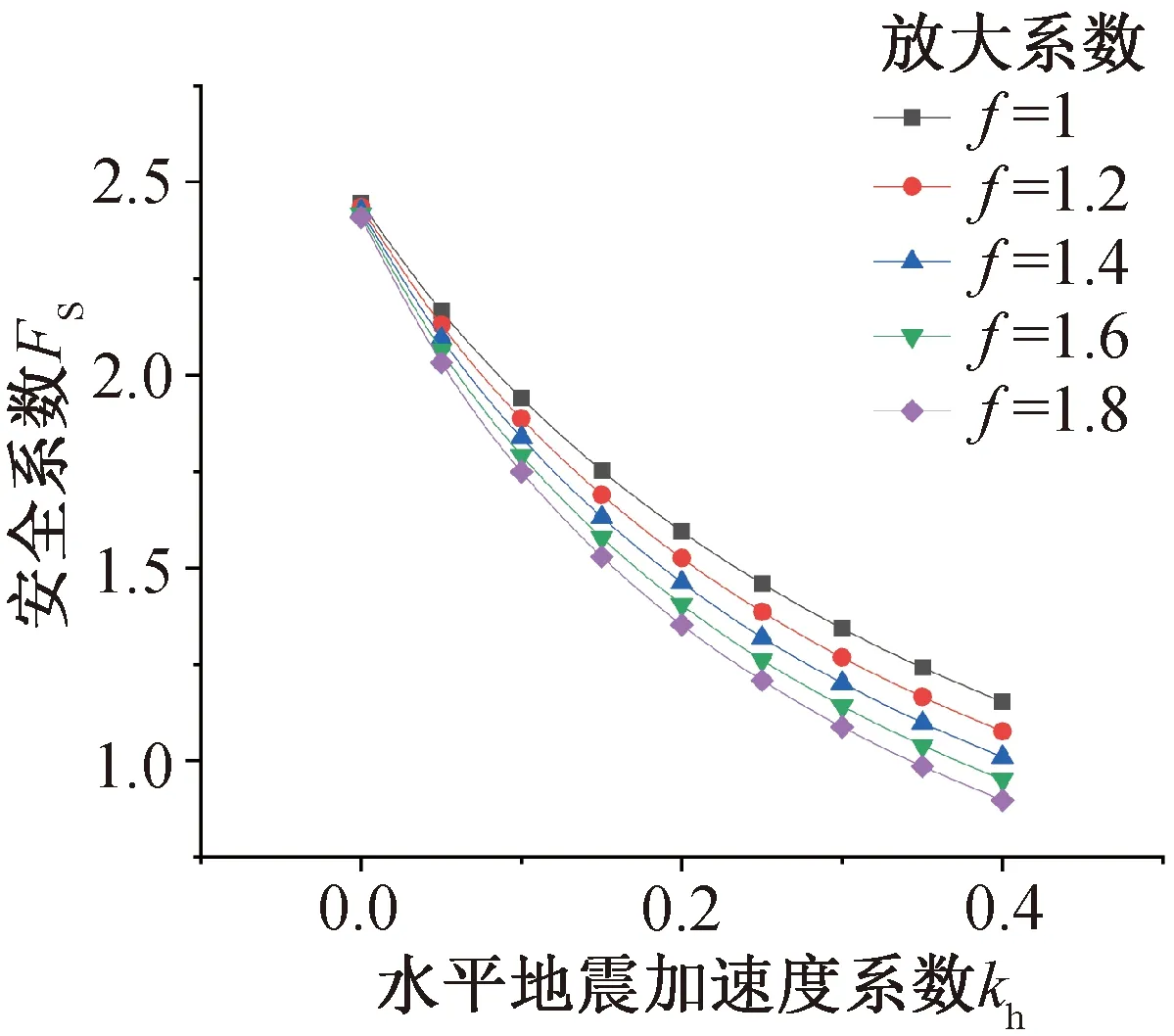
图12 水平地震加速度系数kh对边坡安全系数的影响Fig.12 Influence of horizontal seismic acceleration coefficient kh on slope safety factor coefficient kh on slope safety factor