基于随机Petri网的校园突发事件应急系统性能分析

2022-07-01薛小燕栾尚敏田立勤

现代计算机 2022年8期

张懿，薛小燕，栾尚敏，田立勤

（1.华北科技学院安全工程学院，三河 065201；2.华北科技学院计算机学院，三河 065201）

0 引言

随着国家教育政策的持续发展进步，中国高等院校规模不断扩大，与此同时伴随的人为以及非人为校园突发事件逐渐增多，如自然灾害、实验事故、消防治安等问题，给高校应急管理带来很大挑战。这些问题不仅会对当事人和涉事人造成心理和身体上的巨大伤害，更会对高校的名誉以及社会影响力造成一定的损失，造成一系列的连锁反应。基于以上原因，建设校园突发事件应急系统并进行建模分析对于优化校园应急管理能力，发展校园应急管理体系能力建设有着举足轻重的地位，校园突发事件应急系统的合理使用成为优化校园发展的必然要求，有利于保护学生合法权益，也可以有效预防相关的校园突发事故。一直以来许多研究关注于校园应急管理体系建设，由文献［2］提出2000年撰写的《临危不乱：校园危机管理手册》，在我国香港特别行政区广为使用。以及我国台湾省在2000年发行的《十大校园危机管理手册》，开展了对于台湾中学流行突发事件的针对性研究并进行事件分类，后续提出了许多具备实用性、操作性的应对方案。文献［3］分析了工业安全管理方案的特性，并将其原理应用到校园应急管理体系建设中，建立校园应急事件安全风险评估体系，提出相应措施，完善了中小学校园应急管理能力建设方案。文献［4］从安全系统工程原理与英国校园应急管理体系中得到启发，设计中小学安全风险管理系统并将其分为四个子系统进行系统分析，对于整体系统的管理与风险辨识起到良好作用。文献［5］深入研究事故信息来源以及类别对于区域大众发生响应行为的影响，发现大众往往倾向彼此交流以及听从上级的指示。文献［6］针对突发事件舆论传播模式构建了超网络系统模型，并利用枢纽节点来影响舆论传播模式并分析模型。

以上研究虽然从各种角度分析校园应急管理系统框架建设，但并未形式化建模分析校园应急系统。针对这种不足，可运用随机Petri 网相关理论，构建校园突发事件应急系统安全性能分析的随机Petri 网模型，并利用基于模型的马尔科夫模式对系统性能进行分析，通过调节有关数值变化情况分析系统安全性能可提高的方式。

1 随机Petri网

Petri 网理论由CarlAdamPetri 于1962年在其博士论文中提出，借助计算机技术图形化表示描述异步并发离散系统中的控制流与信息流并进行形式化分析，即在已知变化状态下研究网络整体的输入输出问题。广泛应用于工作流、任务流系统模拟，是利用计算机技术处理系统运行模型的成熟工具，但基本网系统存在无法模拟现实中具有滞后发生特点的事件系统等问题。随机Petri网（stochastic petri nets，SPN）理论由Vautherlin 等人提出，基于引入时间的Petri网理论而来，在变迁（transition）发生时刻与发生完成之间添加一个随机时间，使变迁具备发生速率（firing rate），即在变迁发生时保留“擦除”的Token 一段时间，使Token 输出具备延迟性。所添加的随机时间在指定的分布内可取任意值，离散时间指定为几何分布，连续时间指定为指数分布，每一个变迁都代表着现实系统中的事件，且变迁使能对应着系统状态改变，当某一活动完成或某一逻辑条件得到验证，系统状态就会改变。且多个具备速率的变迁可并行使能，但负指数分布概率密度函数不可能取同一值，所以两个具备速率的变迁不可能同时使能。

由于随机Petri 网与其对应的P/T 网具备的可达图完全一致，所以P/T 网为随机Petri 网的一个特殊子类，可视作所有变迁发生的速率为零，一些针对于P/T网的形式化分析思路与随机Petri 网有相似之处。随机Petri 网可形式化为一六元组SPN=｛，，，，，｝，其中｛，，，，｝为一个P/T 网，λ=｛，，，…，λ｝为变迁平均发生速率集合，即单位时间内发生变迁的平均次数。=｛，，，…，P｝为有限库所集合，=｛，，，…，T｝为有限变迁集合，（×）∪（T×）为库所与变迁之间交互产生的有限状态弧函数，为库所到变迁以及变迁到库所之间的有向弧权值函数，为初始状态具有的Token 模式，Token 的具体数目根据具体系统模型情况而设定。若一个随机Petri 网有界，则有∀∈［＞，∀∈，（）≤，其中为库所最大容量，即保证随机Petri网不会产生溢出。

在系统模型性能分析中首先建立具体案例系统的一个随机Petri 网模型，每一个随机Petri网模型都同构于自身对应的一个一维连续时间马尔可夫模式，之后就可根据马尔可夫模式的稳态概率表达式对于具体案例系统的状态展开性能量化分析。稳态概率是指给定一马尔可夫模式，若在其状态空间中存在一概率分布，使得该分布与状态转移矩阵乘积仍等于该概率分布，这时称该马尔可夫模式处于稳态，而此时的状态转移概率为稳态概率。通过同构得出的马尔可夫模式可以利用含有变迁发生速率的稳态概率表达式计算出各个稳态概率，进而分析系统的安全性能。在有界随机Petri 网中，常返状态是自动非零常返的，且各状态或者是常返的或者是在某一时期后不可达的，若马尔可夫模式中一个状态是常返的，给定充分的时间，系统总是可返回该状态，若不返回则称为滑过状态。

2 校园突发事件应急系统随机Petri网模型

2.1 随机Petri网模型构建

校园突发事件具有毫无征兆、后果严重、影响广泛的特点，建立事故应急系统目的是把传统的应急事故预案制定和实施进行建模形式化分析，可以直观地把监测、组织、指挥、救援、报告等事故处理阶段量化表示，形成清晰的事故处理流程，并可根据事故类型不同来调整模型。而随机Petri 网作为一种处理异步并发系统的系统模型，可以用来表示校园突发事件应急处理的各个过程的发生和之间的联系，且引入时间使得模型中部分变迁具备优先级，更合理地表示实际情况下的事故发生模式。系统可由监控系统、应急指挥系统、安保应急救援系统三部分构成，校园突发事件根据主观性质不同分为人为事故与非人为事故，即可设定反映两种不同事故类型的应急系统流程随机Petri网模型。无事故时，监控系统始终正常运行，应急指挥系统以及安保应急救援系统保持待命状态。当事故发生时，通过校园内搭设的全方位监控系统采集实时画面记录，并迅速上传数据到应急指挥系统，应急指挥系统人员根据监控数据中事故的实际情况以及事故应急预案进行判定并作出实时响应，若事故性质严重则指派安保应急救援系统组织实施应急救援，在救援处理结束之后，对事故内容进行总结以便备案与事故原因的后续调查。若事故性质较轻或者事故在现场被解决完毕，应急指挥系统则可以不需要指派安保应急救援系统前往处理，可直接分析事故成因并进行备案。设立库所集合=｛，，，，，，，，，，，｝，设立变迁集合=｛，，，，，，，，，，，｝，并定义3 个Token，其中各库所以及各变迁表示的含义如表1所示。

表1 随机Petri网模型符号定义

构建的随机Petri网模型如图1所示。

图1 校园突发事件应急系统随机Petri网模型

2.2 模型可达性判定

校园突发事件应急系统随机Petri 网模型中处设置的Token 表示监控系统待命，表示监控系统监测到事故并上传数据，和处的Token表示安保应急救援系统可正常被派出开展救援工作。当事故发生时，监控系统运行并检测到事故，T使能，的Token 输出至，之后输出至表示应急指挥系统接收到事故场景实时信息并准备处理事故。此时变迁，，构成自由选择冲突，在随机Petri 网中，变迁的冲突解与其所设置的时间相关，可通过确定变迁使能的优先次序或者给予不同的变迁以不同的使能条件谓词，当满足谓词时才可使能。通过竞争策略进行系统调度和控制策略是随机Petri 网的优点之一。在此不妨设置优先使能，的Token 输出至，应急指挥系统决定不指派安保救援系统。接下来使能，的Token 输出至，最终输出经过使得较轻事故信息经由应急指挥系统进行备案，使得监控系统恢复初始状态。对严重事故进行系统分析，当输入Token 后，此时令优先使能，应急指挥系统判定严重事故为非人为事故，的Token 输出至。接下来应急指挥中心分析事故严重程度并指派安保救援系统处理，即的Token 输出至，而P的Token 也通过输出至，获得两个Token，表示安保救援系统实施救援行动。处理完毕事故后，的两个Token 输出至与，即安保应急救援系统救援完毕继续待命，且反馈事故信息至应急救援系统，最终的Token令使能到达，即应急指挥系统对事故全程进行分析备案。同上述流程分析人为严重事故随机Petri 网系统，即令T优先使能。最终形成的可达集为：=（1，0，0，0，0，0，0，1，1，0，0，0），=（0，1，0，0，0，0，0，1，1，0，0，0），=（0，0，1，0，0，0，0，1，1，0，0，0），=（0，0，0，1，0，0，0，1，1，0，0，0），=（0，0，0，0，0，0，0，1，1，0，1，0），=（0，0，0，0，0，0，0，1，1，0，0，1），=（0，0，0，0，1，0，0，1，1，0，0，0），=（0，0，0，0，0，0，2，0，1，0，0，0），=（0，0，0，0，0，1，0，1，1，0，0，0），=（0，0，0，0，0，0，0，1，0，2，0，0）。该可达集反映了网系统的各个状态，为后续分析提供支持。

3 校园突发事件应急系统随机Petri网性能分析

3.1 随机Petri网的同构马尔可夫模式

在随机Petri 网模型中，连续可使能变迁的发生速率服从Molly 指数分布，若有个可使能的变迁集合=（，，，…，T），设任意变迁T∈T，T为当前可使能变迁集合，有：

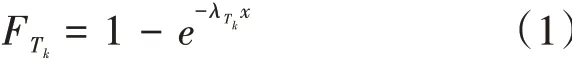
式中≥0为随机设定延迟变量。由于该分布存在无记忆性且系统中存在有限个Token，所以该随机Petri 网的每个Token 可映射为其同构的马尔可夫模式的一个状态表示，在任意一个Token模式下，每一个变迁使能概率不同，设T∈T，则T的使能概率为：

其中λ为T的平均发生速率，λ为可达状态的相关变迁平均发生速率，＞表示可达态是可使能的。面对系统中可使能变迁冲突时利用冲突解决策略设定瞬时速率变迁进行隔离，如在，，冲突时，根据具体状态设定瞬时速率使得其中之一瞬时使能，发生非人为事故时，设定为瞬时变迁，使能优先级大于其他变迁，隔离了与的使能。

对于本随机Petri 网模型设定变迁平均发生速率集合=｛，，，，，，，，，，，｝，根据随机Petri 网模型可达集的弧转换关系以及弧所对应变迁的平均发生速率，可以构造对应的马尔可夫模式以及获取状态转移矩阵的相应参数。以使能的变迁作为有向弧，整理系统全局可达集得出马尔可夫模式如图2所示。

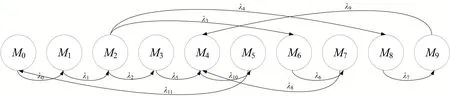
图2 随机Petri网同构马尔可夫模式

在发生严重事故后的整个模拟过程中的变迁为顺序发生，总发生时间为所有变迁发生时间之和，提高任意一个变迁的平均发生速率都可以提高全局发生速率。设马尔可夫模式均衡态下的M的稳态概率为（M），其中∈｛1，2，3，…，｝，若随机Petri 网中有Token 模式的前置与后置之间存在可达性，则有：

其中M，M，M∈［＞，且M［T＞M，M［T＞M。又因为:

由此可得马尔可夫模式稳态概率方程组为：

解此方程组可得出校园突发事件随机Petri网系统各状态下的稳态概率的表达式，后续可进一步通过调节某些变迁发生速率来降低校园突发事件造成的各种危害，提高系统模型优化效率，有利于提高事故处置水平。

3.2 系统性能分析与仿真

实验采用PIPE 仿真平台进行模拟，PIPE 是一个基于Java 开发且遵从PNML 语言的Petri 网分析平台，从逻辑上分为图形交互层、数据层以及分析模块。在分析随机Petri 网时有四步骤：

（1）搜索随机Petri网的状态空间。

（2）消除随机Petri 网运行状态并构造其可达图。

（3）运用同构马尔可夫模式计算稳态概率。

（4）利用稳态概率计算随机Petri 网的量化参数。

在本系统中设定不同的变迁平均发生速率进行系统状态分析，通过假设检验，设定λ=｛6，2，2，3，3，1，4，4，4，4，2，1｝，表示初始阶段监控系统正常运行、响应时间短，相应的变迁发生速率较快，而上传信息阶段严重事故的变迁速率相对较快，且两类严重事故发生后指派应急救援部门和事故处理阶段的变迁速率各自保持同步，最终备案处理变迁速率与非严重事故处理速率同步，根据PIPE 仿真结果，各可达态停留时间见表2。

表2 初始速率集的状态停留时间

此时求得各稳态概率为（）=8/83、（）=24/83、（）=6/83、（）=12/83、（）=6/83、（）=12/83、（）=3/83、（）=3/83、（）=9/166、（）=9/166。表示每个可达态在限定发生速率下的稳定概率，越大则越不稳定，容易发生此状态。改变λ 的值，可分析出随着的增大，即使能次数增多，监控系统处于活跃状态发送紧急情况增多，系统整体处于空闲状态的概率下降，后续处理事故的繁忙概率增加，总结上传信息的概率显著增加。假设其余速率不变，而改变与的值，使λ=｛6，2，5，5，3，1，4，4，4，4，2，1｝，各可达态停留时间见表3。

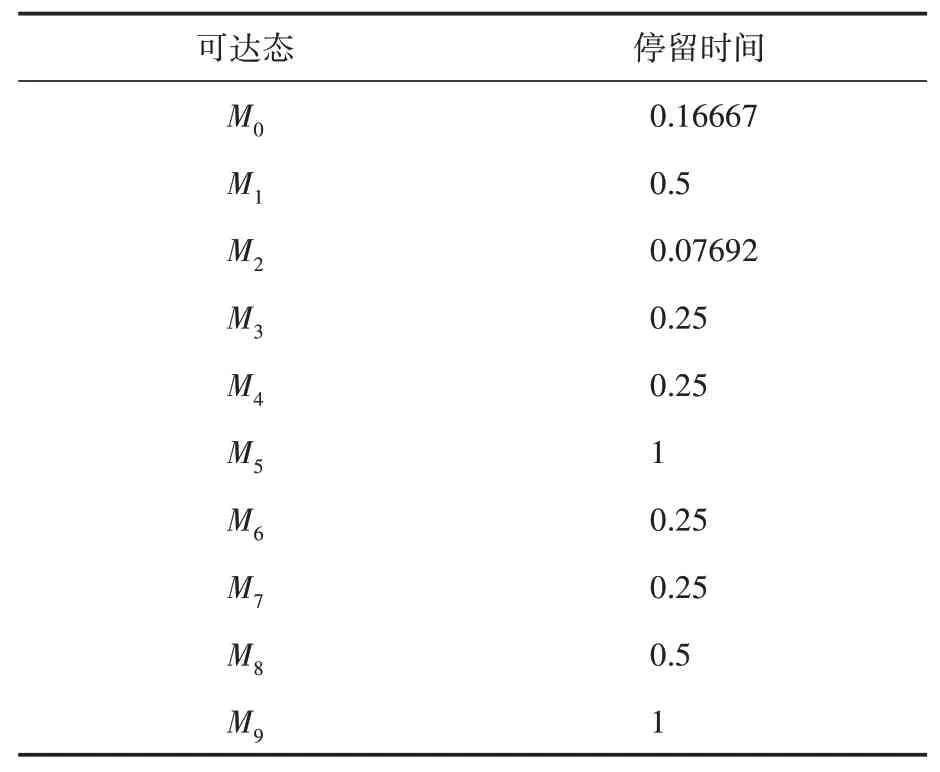
表3 改变λ2与λ3的状态停留时间

此时求得各稳态概率为（）=13/202、（）=39/202、（）=3/101、（）=15/101、（）=15/202、（）=15/101、（）=15/101、（）=15/101、（）=9/404、（）=9/404。表示此时系统判断事故为非严重事故和严重事故的概率增加，指派应急救援系统处理事故的概率增加，不指派的概率减少，且最终事故信息整理上传备案的概率增加，即代表着系统成功完备处理某一类型事故的概率增大，其余状态概率变化正常。在此基础上改变、、以及值，使=｛6，2，5，5，3，1，3，4，5，6，2，1｝，各可达态持续时间见表4。

表4 改变λ6、λ7、λ8以及λ9的状态停留时间

此时求得各稳态概率为（）=26/313、（）=78/313、（）=12/313、（）=60/313、（）=30/313、（）=60/313、（）=20/313、（）=12/313、（）=9/313、（）=6/313。系统判断事故类型为非人为或人为事故概率增加，且事故信息整理上传备案的可达态稳态概率比不指派救援时增加，可凸显出非人为事故和人为事故发生时，相应的应急安保部门作出反应，以及后续救援部门的相关调度，因此采用随机Petri 网方法分析校园突发事故应急系统安全性能时，由于各变迁都有实际的意义，因此可以在系统运行中采取相应措施控制变迁触发速率，来改变系统处于各种状态的稳态概率以达到提高安全性能的目的。