WMAN中的边缘服务器放置研究
2022-07-01赵兴兵赵一帆丁洪伟
赵兴兵,赵一帆,李 波,陈 春,丁洪伟
(1.云南大学 信息学院,云南 昆明 650000;2.云南民族大学 电气信息工程学院,云南 昆明 650000;3.云南民族大学 应用技术学院,云南 昆明 650000)
0 引 言
近年来,越来越多的智能终端在现代社会生活中发挥着重要作用;随着移动互联网快速发展,出现了各种基于网络的新型业务,这二者使得互联网数据量急剧增加,网络流量快速增长,也使得网络的结构和环境变得更加复杂。与此同时,企业和用户对高速传输数据、降低服务时延和快速响应请求提出了更高的要求。此外,由于智能终端计算能力有限,移动应用程序发展受限,急需一种可以将计算迁移到云端进行的方案。边缘计算作为一种新兴技术,具有改善网络结构、提高通信能力、合理分配网络资源的功能,能够有效缓解以上冲突。
边缘服务器(Edge Server,ES)放置、微云放置和计算卸载技术是移动边缘计算中的重要技术。微云放置技术通过在网络的WiFi接入点放置计算机达到卸载用户工作负载的目的;计算卸载致力于将用户的计算任务卸载到远程云处理,以应对终端计算能力不足和容量有限的问题,在一定程度上提高了移动应用程序的性能,然而,远程云通常位于距终端较远的地方,使得终端用户的时延成本非常大;微云放置和计算卸载都有效改善了网络结构。
边缘服务器放置技术通过在策略位置放置具有存储和计算功能的ES,达到改善网络结构和减少用户请求时延的目的,本质是将云端部分功能下沉到网络边缘的技术。
本文主要对移动边缘计算中WMAN环境下的ES放置(Placement of Edge Server in WMAN,WESP)问题进行研究。通过在WMAN中放置ES,可以有效降低网络时延、提高服务质量和节约网络部署成本。
文献[6]设计了一种针对多用户任务卸载的系统模型,提出了基于负载最重优先和用户密度优先的微云放置方法。文献[7]研究了WMAN中有限容量的微云放置问题,并证明了边缘服务器的部署问题是一个NP难问题,当问题规模较小时,提出基于整数线性规划的求解方法。文献[8-9]讨论了微云放置的成本问题,不同的是:文献[8]提出了一种拉格朗日启发式算法对微云进行放置;文献[9]采用改进的贪婪算法予以解决。文献[10]讨论了随机分布情况下的微云放置问题,以尽可能覆盖更多的用户为目标,提出了基于K-Means的放置方法。文献[11]对移动边缘计算中的5G环境进行了建模分析,以最小化时延开销和能量开销为目的,提出了基于等效带宽的ES放置方法。文献[12]对ES放置的能耗问题进行讨论,提出了基于粒子群的放置方法。文献[13]讨论了容量有限的ES放置问题,提出了PACK算法,试图最小化ES与用户之间的时延。文献[14]以优化商业指标为目标,提出了一种基于资源需求预测的ES放置算法。
以上研究成果中,文献[7]使用优化算法解决放置问题,优化的指标包括部署成本、时延、能量等,然而没有关注放置的负载均衡;文献[6]、文献[10]使用聚类算法解决放置问题,然而传统的分类算法在面对WESP问题时,必须被改进以保证放置性能。针对此,本文以优化平均时延和负载均衡为目标,提出一种灰狼优化算法优化K-Means的放置方法以解决WESP问题。
1 问题描述

WESP问题描述:给定一组边缘服务器ES的集合、基站BS的集合,以及每个基站负责的用户集合,在给出的基站集合中寻找一种合理的ES放置方案,然后将基站分配给ES,使得ES放置的平均时延Delay[ES]最小,同时使得所有ES负载的均衡程度Workload_Balance[ES]最小(下文称为负载均衡),目标函数的数学模型为:
Min Delay[ES]()&&Workload_Balance[ES]()(1)式中:为放置方案,即问题的一组解;边缘服务器的平均时延是所有ES传输时延的平均值,可由式(2)表示:

由以上分析可知,只需求出单个ES的传输时延便能得到ES的平均时延。而单个ES的传输时延可以表示为:

式中[]表示移动用户请求到达ES的传输时延。
同理,单个边缘服务器的负载Workload[ES ]可表示为:

阿特金森福利指数由英国经济学家阿特金森于1979年提出,常被用在经济学领域中度量收入不平等程度,其表达式如下:

式中:是平均收入;y是某个群体或某人的实际收入;表示不平等厌恶参数,反映社会对于不平等的厌恶程度。考虑ES负载均衡的意义与阿特金森指数的相似性,将其引入ES负载均衡的计算,表达式如下:

式中:ˉ为ES的平均工作负载;设置为2。
解决WESP问题有两个关键步骤:对ES进行放置、对基站进行分配。
本质是在给定的基站集合中寻找基站到ES的映射关系,可以理解为:首先确定ES的布局,然后根据ES的布局对所有基站划分子集。
为了解决WESP问题,划分基站子集时必须满足以下约束条件:
1)任意基站子集BS =∅;
2)所有基站子集的交集∩BS =∅;
3)所有基站子集的并集∪BS =BS;
4)任意用户请求到达ES的传输时延[]小于用户能够接受的最大传输时延Access_Delay。
当满足以上约束条件时,将WESP问题的数学模型表示为:

2 灰狼优化与K-Means结合的部署算法
灰狼优化(GWO)算法是Mirjalili提出的新型群体智能优化算法,在GWO中,灰狼的位置代表优化问题的可行解。自然界中狼群的社会结构可以分为4个阶层,,和,其中,,,处于优势地位,为领导狼,负责管理狼群,支配狼群的行为;狼处于受支配地位,负责平衡种群数量和包围猎物等。狼群的狩猎过程即是优化问题的过程,狩猎可以分为以下三个过程:
1)通过不断移动位置,跟踪、包围猎物
数学模型为式(8)、式(9),其中,式(8)表示灰狼个体与猎物的距离,式(9)表示狼群个体更新位置。

式中:X ()为猎物的位置向量;X ()为灰狼的位置向量;为系数;为迭代次数;为系数。,由式(10)和式(11)计算。

式中:,均是[0,1]之间的随机数;为算法控制参数,从2线性减小到0,当较大时,算法具有较强的全局开发能力,当较小时,算法具有较快的收敛速度。

式中:为当前迭代次数;为最大迭代次数。
2)不断追逐猎物,直到猎物停止移动,确定最佳的狩猎位置
数学模型为式(13)~式(15):

式中:D(∈{,,})表示狼、狼和狼与猎物之间的距离。狼、狼和狼的地位由适应度函数值确定,根据适应度函数值确定的最优解、优解和次优解分别为狼、狼和狼;X表示狼、狼和狼的位置;,和为系数,由式(11)得到。

式中:,和为系数,由式(10)得到;,和分别为根据狼、狼和狼计算得到的候选解位置。

根据式(15),由狼、狼和狼得到候选解狼,确定为最佳的狩猎位置。如果狼的位置比优势狼更优,则对优势狼进行更新;否则,不更新。
3)攻击猎物
当确定最佳的狩猎位置后,灰狼通过攻击完成狩猎过程。当从2线性减少到0的过程中,的值在[-,]内变化,的变化决定灰狼的行为,当 ||<1时,狼群的行为表现为攻击猎物;当 ||>1时,狼群的行为表现为向外探索,开发更优的解。
GWO在狼、狼和狼的指导下,不断更新狼群位置寻找问题的最优解;在迭代过程中,狼群的社会等级制度确保了狼保存得到的最优解;狩猎方法允许候选解定位猎物的可能位置;GWO的控制参数较少,参数的设定保证了算法的收敛性与全局搜索能力。GWO的流程图如图1所示。

图1 GWO的流程图
K-Means是一种经典的聚类算法,特点是可以对聚类数量进行指定并且将欧氏距离作为相似性的评价指标,欧氏距离越小,相似性越小,表明聚类效果越好,经过迭代求解,最终将距离较近的样本数据归为一类。传统K-Means方法描述为:
1)根据经验指定聚类的数量,随机初始化个聚类中心=(,,,c),转入步骤2);
2)根据式(16)计算每个样本数据到所有聚类中心的欧氏距离,并将其划分到最近的聚类,转入步骤3);
3)根据每个聚类中的样本数据重新计算该类的聚类中心,并将其作为新的聚类中心,转入步骤4);
4)判断步骤3)的聚类中心是否变化,若变化,转入步骤2);否则,退出循环,得到聚类结果。
任意一个样本数据S和聚类中心c的欧氏距离的表达式为:

K-Means能够对特征较多的大型数据集进行分类,并且计算速度快,不足之处在于对初始聚类中心敏感,容易陷入局部最优。
结合以上分析可知,K-Means算法的思想与WESP问题类似,可以将WESP问题理解为以ES放置位置为聚类中心的聚类问题,所以可以使用K-Means解决WESP问题。但K-Means方法存在对初始聚类中心敏感和容易陷入局部最优的问题,所以本文提出GWO-KM改善相关问题并解决WESP问题。
3 GWO-KM算法
使用GWO优化K-Means的实质是优化K-Means的聚类中心,在K-Means的每次迭代中,使用GWO对聚类中心进行优化。使用GWO算法需要设定适应度函数,以便对种群进化方向提供指导,结合K-Means方法,将每个聚类的所有类内样本数据距离之和作为适应度函数(注意,由于解决WESP问题是为在现实环境中放置ES提供策略,所以模拟样本数据代表基站的经度和纬度坐标,任意两个由经度和纬度表示的坐标=(W,J)和=(W,J)之间的距离(,)用式(17)表示),将适应度函数定义为式(18)。

式中:为地球半径;为样本数据集合。
使用GWO-KM算法解决WESP问题的步骤如下:
Step1:根据样本数据和经验指定聚类数量,转入Step2;
Step2:设置GWO算法的参数,包括最大迭代次数、种群规模、聚类中心参数的范围,转入Step3;
Step3:根据Step2的参数范围初始化只狼作为种群,每只灰狼表示个聚类中心,是GWO的一组解,纬度为×dim,dim为样本数据的特征数量,转入Step4;
Step4:根据式(18)计算每只狼的适应度函数值,并将适应度值最小的3只灰狼依次确定为狼、狼和狼并保存其适应度值和位置,转入Step5;
Step5:根据狼、狼和狼的位置,由式(10)~式(15)更新所有灰狼的位置,转入Step6;
Step6:将狼作为K-Means的聚类中心,根据式(16)计算每个样本数据到所有聚类中心的距离,并将其划分到距离最小的聚类,保存每个分类,转入Step7;
Step7:根据式(18)计算每只狼的适应度函数值,并依次与狼、狼和狼比较,若新灰狼的适应度函数值更小,则更新狼、狼和狼的位置和适应度函数值,转入Step8;
Step8:判断当前迭代次数是否达到,若达到,退出循环,转入Step9;否则,转入Step5;
Step9:根据狼的位置和Step6中保存的分类,找出每个聚类中不重复、与该类聚类中心最近的样本数据作为ES的放置位置,并将其余的样本数据分配给该ES,转入Step10;
Step10:根据Step9的放置关系和分配关系,以及式(2)~式(6),计算负载均衡和平均时延。
使用GWO-KM解决WESP问题结合了分类和优化的思想。为ES分配基站的过程与基于距离分类的过程类似,使得GWO-KM对解决WESP问题表现良好;此外,GWO-KM的分类是独立、非空的分类,能够很好地满足式(7)的约束条件。需要注意的是:ES的放置位置是某个确定的基站位置,是不能改变的;而K-Means的聚类中心是可以改变的,并不是某个确定的样本数据。所以需要在迭代结束后,根据聚类中心重新确定ES的放置位置。
4 仿真实验与结果分析
仿真环境:实验环境配置为IntelCorei7-9750H CPU 2.60 GHz处理器,操作系统为Windows 10 professional 64位,运行环境是Python 3.7.6。
核心参数设置:=800,=60,Workload[ES ,USER ]∈[200,600]。
场景模拟:基于系统模型建立了一个矩形区域作为实验的仿真场景,横纵坐标的单位均是km。仿真场景中分布着500个服从泊松分布的基站。假设这些基站能够覆盖此区域内所有移动用户。实验区域为:
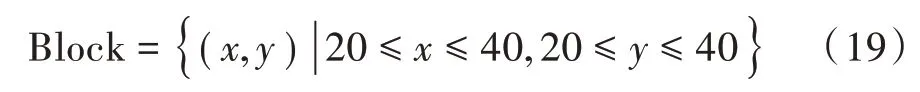
对比算法:为了显示实验的客观性,分别选取三种典型的算法Random、Top-K和K-Means与本文的GWO-KM算法对比。
测试指标:根据系统模型,对算法的负载均衡和平均时延进行测试。
实验1:设置基站的数量为500,不断增加ES的数量,测试各种算法的平均时延(注:为了简化实验,本文以距离作为时延对算法进行测试,并且忽略移动用户请求接入基站之前的无线时延)。
实验1的结果如图2所示。图2中,横坐标为ES的数量,纵坐标为平均时延。

图2 各类算法的平均时延比较
ES的数量为30个,Random的平均时延约为1.8 km,Top-K的平均时延约为11.3 km,K-Means的平均时延约为1.3 km,GWO-KM的平均时延约为1.2 km,相比于其余三种算法分别降低了约33.3%,89.4%和7.6%。
ES数量为50个,Random的平均时延约为1.2 km,Top-K的平均时延约为10 km,K-Means的平均时延约为1 km,GWO-KM的平均时延约为0.8 km,相比其余三种算法分别降低了33.3%,92%和20%。
ES数量为60个,Random的平均时延约为1.1 km,Top-K的平均时延约为10.5 km,K-Means的平均时延约为0.8 km,GWO-KM的平均时延约为0.7 km,相比于其余三种算法分别降低了36.3%,93.3%和12.5%。
实验1分析:随着ES数量增加,Random、K-Means和GWO-KM的平均时延减少。这是因为在基站数量一定的情况下,随着ES数量增加,基站的潜在可分配ES数量也增加,基站将被分配给更近的ES;GWO-KM比K-Means表现更好的原因是在每次迭代过程中使用了GWO优化聚类中心;Top-K的时延始终远远大于其余三种算法,因为Top-K的放置依据是基站的负载,忽略了距离,而基站之间的距离是ES放置的重要依据。
实验2:设置基站的数量为500,不断增加ES的数量,测试各类算法负载均衡的变化。
实验2的结果如图3所示。图3中,横坐标为ES的数量,纵坐标为负载均衡。

图3 各类算法的负载均衡比较
ES的数量为30个,Random的负载均衡约为0.97,Top-K的负载均衡约为0.78,K-Means的负载均衡约为0.82,GWO-KM的负载均衡约为0.74,相比其余三种算法分别降低了约23.7%,5.1%和9.7%。
ES的数量为40个,Random的负载均衡约为0.68,Top-K的负载均衡约为0.39,K-Means的负载均衡约为0.71,GWO-KM的负载均衡约为0.58,相比Random和KMeans分别降低了约14.7%,18.3%;Top-K的负载均衡比GWO-KM减少了0.18。
ES的数量为60个,Random的负载均衡约为0.28,Top-K的负载均衡约为0.11,K-Means的负载均衡约为0.19,GWO-KM的负载均衡与Top-K接近,相比Random和K-Means分别降低了约60.7%,42.1%。
实验2分析:随着ES数量增加,各类算法的负载均衡呈现线性减少的趋势,这是因为当基站的数量一定时,所有基站的总负载也是一定的,所以每个ES的负载也相应减少;而单个基站负载相差不大,所以每个ES负责的基站数量越少,ES的负载均衡越优。Top-K在ES数量为40和50时,负载均衡比GWO-KM更优,说明Top-K牺牲了平均时延,但在负载均衡上表现很好,具备一定的合理性。
以上两组实验的结果说明,GWO-KM相比传统的K-Means性能有所改进,有更好的聚类效果;Top-K虽然在负载均衡上有很好的表现,但在平均时延上表现极差,相比GWO-KM,后者更加适合解决WESP问题。综合来说,Random的表现最差,显然不适合解决WESP问题,所以,相比于其余算法,GWO-KM更适合解决WESP问题。
5 结 语
本文对WMAN中的边缘服务器放置问题进行了研究和分析,将其建模为优化负载均衡和平均时延的问题,通过分析该问题的特点,发现其与分类问题类似,提出了基于灰狼优化K-Means的方法予以解决。GWO-KM使用GWO算法对传统K-Means算法的聚类中心进行优化,改善了K-Means易受初始聚类中心影响和容易陷入局部最优的问题。虽然本文提出的算法在解决WESP问题时表现良好,但仍有以下工作需要改进:WMAN中,移动用户的位置不是固定的,而是变化的,考虑用户的移动性是下一步工作的重点;真实的WMAN中,基站分布情况更加复杂,是模拟数据集不具备的,使用真实的网络数据集进行仿真也是今后工作的重点。
