基于DH参数的机器人运动学建模及参数辨识
2022-07-01邱光祥



摘 要:以KUKA Nano机器人为研究对象,采用DH法建立了机器人正向运动学模型,并利用Matlab Robotic Toolbox进行了仿真验证;通过对机器人定位误差影响因素进行分析,建立了机器人误差模型;阐述了单关节运动学参数辨识方法,采用轴线法对机器人运动学参数进行了辨识实验,得出了机器人各个关节的实际DH值,为后续机器人精度分析与误差补偿提供了理论基础。
关键词:工业机器人;运动学模型;误差模型; DH参数辨识
1引言
工业机器人自诞生以来,在制造业中发挥了重要作用。2013年麦肯锡研究报告指出机器人将带来每年上万亿美元的效益;2016年的达沃斯论坛指出机器人将是一个新的工业革命。近年来,随着“工业4.0”和“中国制造2025”的提出,机器人在现代制造领域的重要性也体现得越来越明显。特别是工业机器人在加工领域也得以采用,工业机器人具有灵活性好、加工范围大、成本低的优点。但工业机器人自身结构的影响,导致机器人的定位精度成为制约机器人发展的关键因素。工业机器人的重复定位精度较高,现有工业机器人能够达到±0.05mm,然而其绝对定位精度往往只有2~3mm;提高工业机器人的绝对定位精度有误差预防法和误差补偿法两类,由于前者对设计和制造水平有极高的要求且经济成本较高,目前通常采用后者。为此建立机器人的运动学模型和误差模型,并对误差来源进行定量分析就显得尤为重要。
2机器人运动学建模与仿真
2.1 基于DH参数的机器人运动学建模
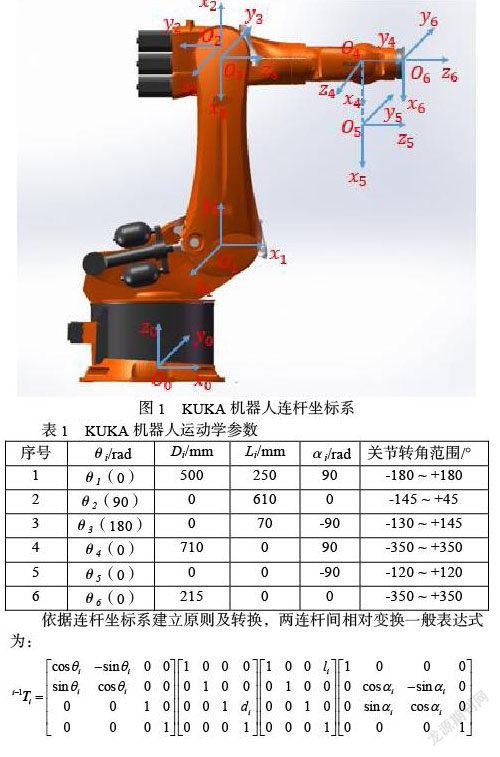
以KUKA机器人为研究对象,依据《机器人技术基础》坐标系建立原则进行建模,结合机器人的结构尺寸及所定义的连杆坐标系,建立该机器人的各个连杆坐标系,如图1所示,表1为在该机器人该状态下的DH参数表:
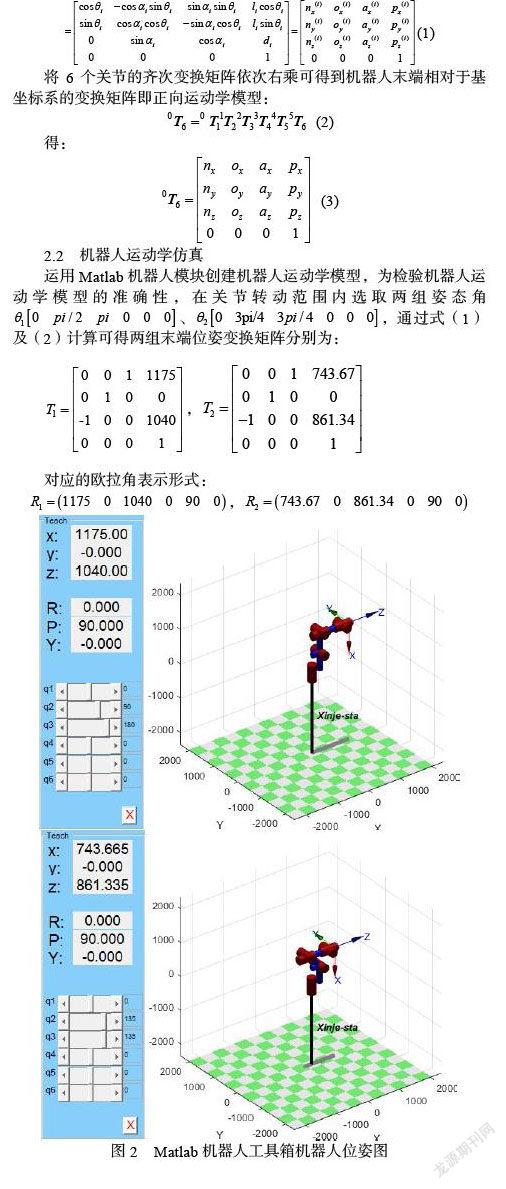
将6个关节的齐次变换矩阵依次右乘可得到机器人末端相对于基坐标系的变换矩阵即正向运动学模型:
2.2 机器人运动学仿真
运用Matlab机器人模块创建机器人运动学模型,为检验机器人运动学模型的准确性,在关节转动范围内选取两组姿态角通过式(1)及(2)计算可得两组末端位姿变换矩阵分别为:
对应的欧拉角表示形式:
两组机器人的实际位姿和计算结果一致,验证了上述机器人运动学建模过程是正确的。
3机器人运动学误差建模
3.1 机器人误差分析
据相关研究,Renders等指出非几何因素对机器人定位误差影响占比10%左右。Hyun-Kyu等指出其中几何参数误差对机器人末端的定位误差占比可达80%,为此研究主要集中在建立机器人运动学误差模型方面。Knasinski等通过研究发现机器人关节转角误差对机器人定位误差影响可达90%,成为影响机器人定位精度最主要的因素。众多研究表明机器人的几何因素引起的定位误差是其主要因素,因此将对机器人几何误差进行建模。
3.2 误差建模
当一个坐标系由原始坐标系平移而来,且平移量较小,称为微分平移,即可表示为:
(4)
微分旋转即是绕空间中某一矢量,进行微量旋转,可用,表示,其中,可分解为分别绕X、Y、Z三轴的旋转组合,假设绕X、Y、Z三轴旋转分别定义为。此时有。由于旋转量很小,故可作如下简化:
连杆绕空间内某一轴,旋转的微分运动可表示为:
(5)进行微分变换后的位姿可表示为:
(6)使用修正的DH模型,通过加入一个绕Y轴转动的参数,约定当两连杆不平行时,其余模型定义与DH模型一致,其相邻坐标系转换矩阵为:
(7)齐次变换矩阵中有四个参数,对于转动关节而言,只有是变量,其余为常量。现以转动关节为例,根据微分理论有:
(8)式分别对各参数求偏导,是实际值与理论值的微小偏差,
同理可求出
式(8)也可写成:
![]() (10)
(10)
其中,是相邻连杆微分变换矩阵。
按照连杆微分变换,对于自由度的串联机器人,由于各个连杆的DH参数与理论DH参数不一致,在机器人基座坐标系下,机器人末端的坐标变换可表示为:
(11)
4机器人运动学参数标定
通过逐个辨识各个关节的运动学误差是辨识六个关节的实际DH参数最直接的方法,单独运行每个关节来获取该关节的实际DH参数。在机器人单轴运动任意一个关节且锁定其它关节,利用激光跟踪仪可以获得该关节的实际轴线,依次建立起六个关节的关节坐标系,依次辨识出六个关节的实际运动学参数。
4.1 单关节运动学参数辨识
1)非平行关節坐标系的建立
非平行关节建立坐标系,机器人各关节坐标系为,利用关节和关节来建立关节坐标系,轴为平面辨识得到的法向量,轴为关节轴线和关节轴线的公垂线方向,关节轴线和关节轴线的公垂线与关节轴线的交点作为坐标系原点,可以利用右手定则确定,即是轴与轴的叉乘向量。
2)平行关节坐标系的建立
平行关节建立坐标系,如图4所示,已知坐标系与关节轴线向量,利用坐标系的平面来构造辅助平面,关节轴线与该平面的交点作为坐标系的原点,利用与的连线来构造辅助向量![]() ,轴为平面辨识得到的法向量,辅助向量与的公垂线作为轴,可以利用右手定则确定,即是
,轴为平面辨识得到的法向量,辅助向量与的公垂线作为轴,可以利用右手定则确定,即是![]() 轴与轴的叉乘向量。
轴与轴的叉乘向量。
杆件扭转角![]()
(16)
杆件转角、杆件长度、杆件偏移量,的计算同上。
4.2 机器人运动学参数标定实验
实验平台由KUKA机器人和API激光跟踪仪组成,该型号的激光跟踪仪的测量精度为![]() ,能够满足实验的需求。本次测量实验为研究各关节的实际DH参数,每次只转动其中一个关节,保持其他关节不动,利用激光跟踪仪来实时测量机器人末端的实际位置。实验后在跟踪仪数据分析软件中拟合结果如图5所示:
,能够满足实验的需求。本次测量实验为研究各关节的实际DH参数,每次只转动其中一个关节,保持其他关节不动,利用激光跟踪仪来实时测量机器人末端的实际位置。实验后在跟踪仪数据分析软件中拟合结果如图5所示:
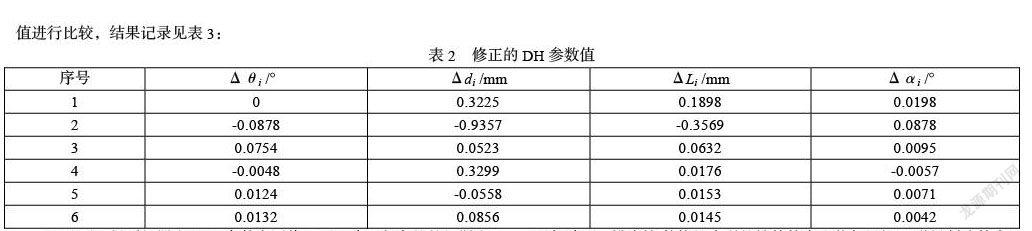
根据DH参数的定义规则来确定各杆件参数值的大小,并与理论值进行比较,结果记录见表3:
至此可以得到机器人DH参数实际值,可以建立起完整的机器人运动学误差模型。
5小结
针对KUKA Nano机器人利用DH模型建立了机器人运动学模型及DH参数;讨论了影响机器人定位误差的各种因素,建立了机器人运动学误差模型,为后续研究准备理论基础;由于实际定位误差的存在,理论DH参数必然存在偏差,因此运用轴线法辨识了机器人各关节的运动学参数,阐述了机器人平行关节与非平行关节的坐标系建立方法,并辨识出了实际的DH参数,为后续机器人定位误差的补偿奠定了基础。
参考文献
[1]丁汉. 机器人与智能制造技术的发展思考[J]. 机器人技术与应用,2016,4:7-10.
[2]Chen Y, Dong F. Robot machining: recent development and future research issues[J]. The International Journal of Advanced Manufacturing Technology, 2013, 66: 1489-1497.
[3]Tomas Olsson,Anders Robertsson,Gilbert Ossbahr, et al. Cost-efficient drilling using industrial robots with high-bandwidth force feedback[J]. Robotics and Computer Integrated Manufacturing, 2009, 26 (1): 24-38.
[4]杨建国,姚晓栋.数控机床误差补偿技术现状与展望[J].世界制造技术与装备市场,2012(3):64-71,95.
[5]熊有伦. 机器人技术基础 [M]. 武汉:华中科技大学出版社,1996.
[6]RendersJ.M, Rossignol E. Kinematic calibration and geometrical parameter identification for robots[J].IEEE Transactions on Robotics and Automation: A publication of the IEEE Robotics and Automation Society,1991,7(6):721-732.
[7]Hyun-Kyu Lim,Dong-Hyeok Kim,Sung-Rak Kim, et al.A Practical Approach to Enhance Positioning Accuracy for Industrial Robots[C] //ICCAS-SICE International Joint Conference, 2009:2122-2127.
[8]Knasinski A.B, Judd R.P.A technique to calibrate industrial robots with experimental verification[J].IEEE Transactions on Robotics and Automation: A publication of the IEEE Robotics and Automation Society,1990,6(1):20-30.
作者簡介:
姓名:邱光祥(1995.10),性别:男,民族:汉,籍贯:江西省,职务/职称:助理工程师,学历:硕士研究生,单位:上海航天控制技术研究所,研究方向:工艺技术。
