海底管道储存和船舶运输时允许堆放层数计算方法

吴业卫

海洋石油工程股份有限公司，天津 300461

1 概述

如图1所示，海底管道由钢管及外部涂层组成，外部涂层包括防腐涂层和水泥配重涂层，在海底管道存储及运输过程中，如果对海底管道的堆放层数不加以限制，海底管道的自身重量可能会造成钢管受压过量变形、椭圆度超标、外部涂层受到损伤，对海底管道的后续使用造成不利影响[1]。

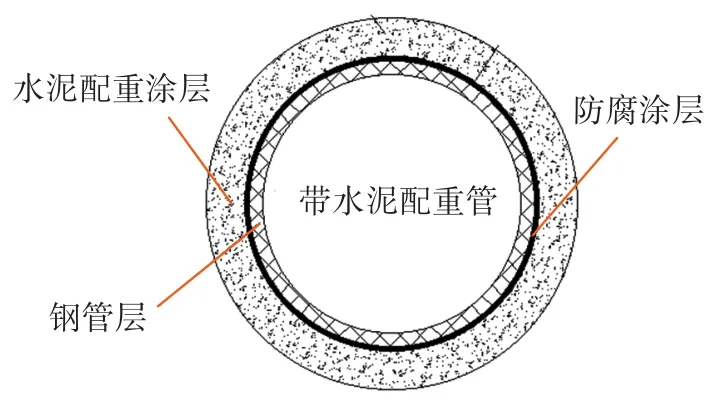
图1 海底管道管体截面

在管道铺设过程中，由运输驳船将管道运输至铺管船，铺管船甲板可以存储部分海底管道，如果铺管船和运输驳船甲板可以尽可能多地存放海底管道，对于长距离的管道铺设项目，则可以在一定程度上减少运输驳船的航次，从而获得一定的经济效益。

对海底管道涂敷工厂来说，海底管道的堆放也是生产过程中必须认真考虑的问题，现有的存储场地能否堆放一定生产周期内的管道，将直接影响后续管道生产的正常组织。

对于管道陆地生产和海上施工而言，需要对管道允许堆放层数进行计算，既不造成钢管和外部涂层的损伤，又能最大限度地利用现有场地及船舶资源，从而最大程度地创造经济效益。

关于管道允许堆放层数计算方法已有一些相关文献，可以在管道钢管应力限制条件下进行允许堆放层数的计算，但没有考虑管道涂层应力的限制条件。本文利用Roark应力应变公式，分别推导出了管道钢管和管道涂层应力限制条件下管道允许堆放层数的计算公式，堆放层数应选择计算结果中的最小值，以保证堆放管道钢管及其涂层的安全。

2 管道堆放受力分析

2.1 最底层管道受力分析

一般情况下，管道堆放采用图2所示的连续堆积方式，管垛层间能够咬合紧密，位于管垛最底层的管道承受最大的上部压力；除此之外，针对最底层管道的受力分析，还需考虑其自身重量，最底层管道与底部接触点的支反力数值等于上部管道的压力和自重的合力，如图3所示。

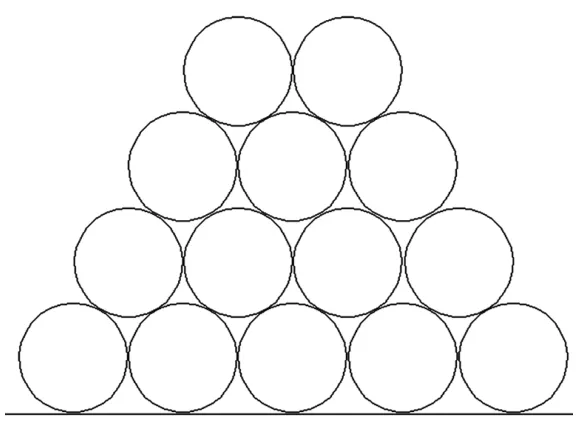
图2 管道堆放形式

图3 最底层管道受力分析

按照图3对最底层管道进行受力分析，可以得出：P=2Fn-1cosθ+W。对于层间咬合紧密的管垛，可令层间咬合角度θ为30°，可以得出：

式中：P为最底层管道与底部接触点的支反力，n为管垛层数，W为管道的自身重力，Fn-1为最底层管道承受的上部管道压力。

为求出最底层管道与底部接触点的支反力P，需要对最底层管道承受的上部管道压力Fn-1进行求解。

2.2 最底层管道上部压力求解

通过对管垛的受力分析可知，管道之间通过相互咬合接触将自身重量及承受的上部管道压力传递到下层管道，为求解最底层管道上部压力，需要按照图4对倒数第二层管道进行受力分析。

图4 倒数第二层管道受力分析

管道在y轴方向受力为力学平衡，可以得出：2Fn-1cosθ=2Fn-2cosθ+W（式中：Fn-2为倒数第二层管道受到的上部管道压力，θ为层间咬合角度），因此：Fn-1-Fn-2=W/（2 cosθ）。

可以看出，不同层管道受到的上部管道压力成等差数列，因此最底层管道受到的上部管道压力为：Fn-1-Fn-2=（n-1）W/（2 cosθ）。对于层间咬合紧密的管垛，令θ为30°，可以得出：

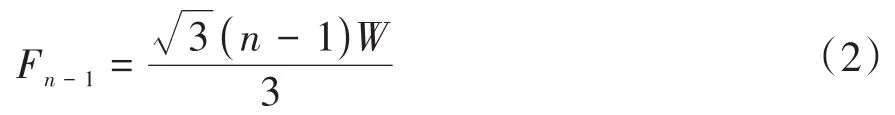
联立式（1）和式（2），可以得出：

3 钢管应力限制条件下管道允许堆放层数计算

最底层管道受到上部管道压力和自身重量的影响，管道钢管层应力最大值应出现在钢管最低点位置，可以分别求出由于上部管道压力和自身重量在该点产生的应力，然后相加得出该点的应力值，该应力值为管道钢管层受到的最大应力。

对于上部管道压力在最底层管道产生的最大弯矩值MC1，可以根据Roark应力应变公式求解[2]：

式中：RS为管道钢管的半径。

对于层间咬合紧密的管垛，可令θ为30°,将式（2）代入式（4）可以得出：

式中：DS为管道钢管的直径。

对于最底层管道自重产生的最大弯矩值MC2，也可以根据Roark应力应变公式求解[2]：

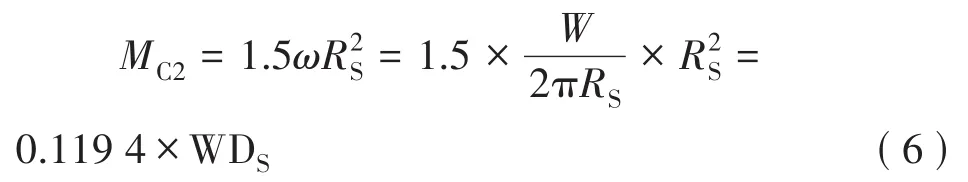
式中：ω为单位弧长的管道自身重力。

最底层管道受到的最大弯矩值应为上部管道压力和管道自重在管道最低点产生的弯矩之和，由此可得出，最底层管道在最低点处承受的弯矩MC为：

根据材料力学公式，已知最底层管道在最低点处的最大弯矩值，可以求出该位置的最大应力σC[3]：

式中：WZ为抗弯截面模量，它的值只与截面的几何形状有关，对于矩形截面的抗弯截面模量WZ，按式（9）计算：

式中：b为承担弯矩的管道截面宽度，t为管道钢管厚度。

将式（7）和式（9）代入式（8），可以得出：

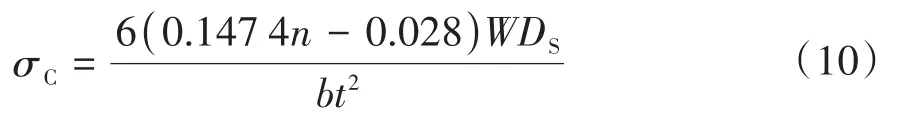
在管道堆放时，为保证堆放区域平整及管道吊装的方便，通常会在管垛底部布置垫木等支撑，在这种情况下，管垛的重量将全部由底部支撑承担，针对这种情况，需要对式（10）进行修正，修正结果如下：

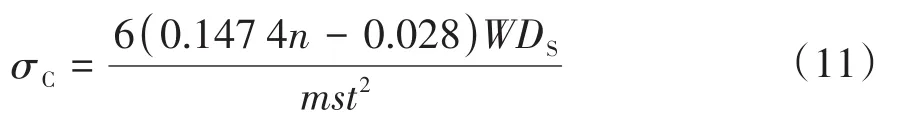
式中：m为支撑的数量，s为支撑的宽度。

为使管垛堆积层数不对管道钢管造成损伤，最底层管道钢管受到的应力应不超过钢管的许用应力[σS]：

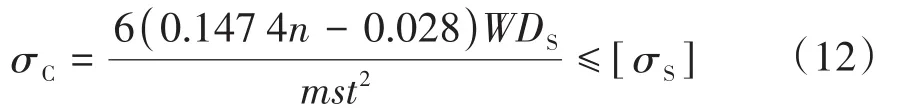
通过式（12）可以得出在不损伤管道钢管层的情况下，管垛的允许堆放层数n：

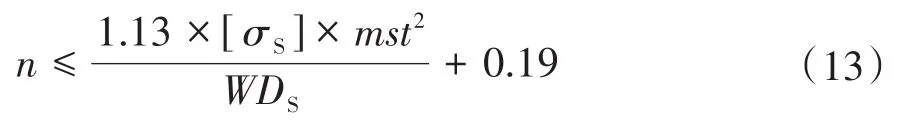
式中：n为管垛层数，是满足式（13）的最大整数；[σS]为钢管的许用应力。

4 涂层应力限制条件下管道允许堆放层数计算

最底层管道受到上部管道压力和自身重量的影响，所产生的涂层应力最大值应出现在最底层管道，最底层管道分别与上部管道和底部支撑接触，可以分别对这两处区域涂层应力进行研究计算，以得出管垛的允许堆放层数[4]。

4.1 最底层管道与上部管道接触区域应力计算

最底层管道与上部管道的接触可以看作是圆柱体与圆柱体的接触，根据Roark应力应变公式[2]，最底层管道与上部管道的接触区域的最大应力σmax1为：

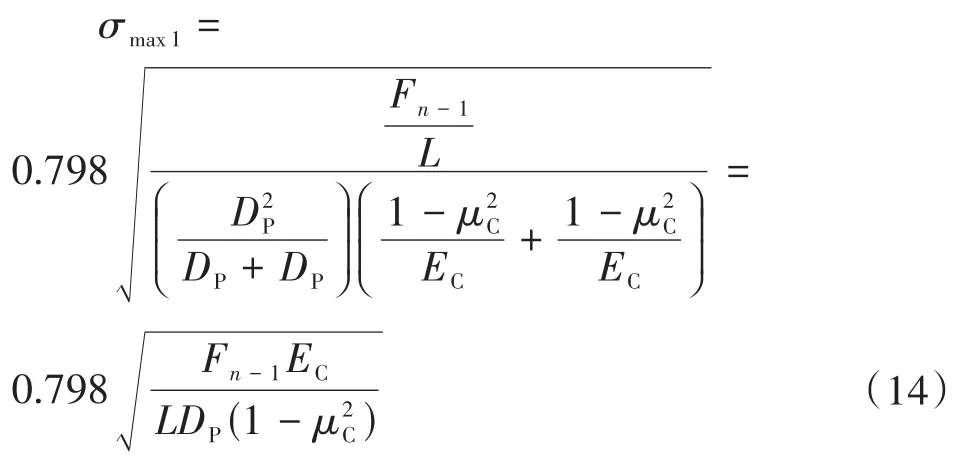
对于层间咬合紧密的管垛，将式（2）代入式（14），可以得出：

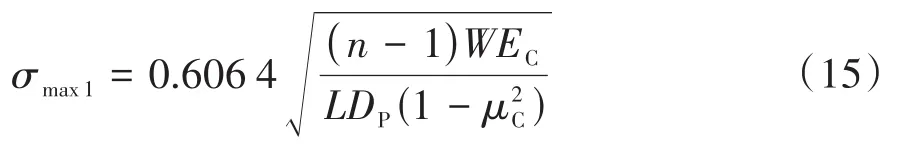
为使管垛堆放层数不对管道涂层造成损伤，最底层管道涂层受到的应力应不超过管道涂层的许用应力[σC]：

通过式（16）可以得出在不损伤管道涂层的情况下，管垛的允许堆放层数n：

式中：n为管垛层数，是满足式（17）的最大整数；DP为包含外部涂层的管道直径；μc为管道涂层的泊松比；Ec为管道涂层的弹性模量；L为管道的长度；[σC]为管道涂层的许用应力。

4.2 最底层管道与底部支撑接触区域应力计算

最底层管道与底部接触区域可以看作是圆柱体与平板的接触，根据Roark应力应变公式[2]，最底层管道与底部接触区域的最大应力σmax2为：

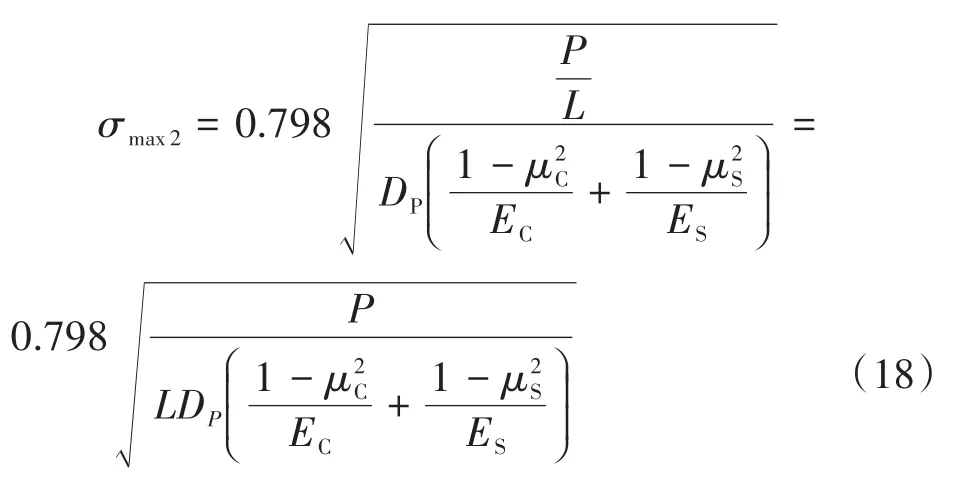
对于层间咬合紧密的管垛，将式（3）代入式（18），可以得出：

同样，对于管垛底部采用支撑的情况，管垛的重量将全部由底部支撑承担，针对这种情况，需要对式（19）进行修正，修正结果如下：

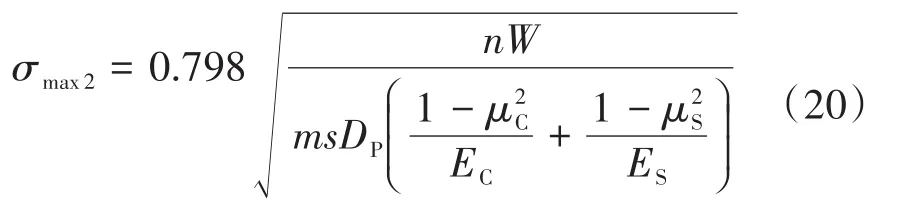
为使管垛堆放层数不对管道涂层造成损伤，最底层管道涂层受到的应力应不超过管道涂层的许用应力[σc]：

通过式（21）可以得出在不损伤管道涂层的情况下，管垛的允许堆放层数n：

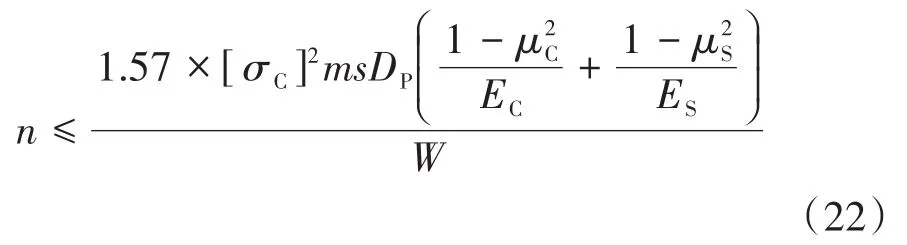
式中：n为管垛层数，是满足式（22）的最大整数；μs为管道底部支撑的泊松比；Es为管道底部支撑的弹性模量。

5 结束语

最底层管道受到的上部管道压力最大，也最易出现管道钢管层和涂层损伤，本文通过对最底层管道的受力分析，得出了最底层管道受到的上部压力，钢管层的最大应力由上部管道压力和管道自重产生的应力组成，计算过程中考虑所有载荷全部由底部管道钢管层承受，利用Roark应力应变公式求出上部管道压力和管道自重产生的最大弯矩，通过最大弯矩求出钢管层的最大应力，从而求出管垛允许堆放层数。

为计算管垛允许堆放层数，还应考虑管道外部涂层的限制，本文同样根据Roark应力应变公式，分别对最底层管道和上部管道接触区域，最底层管道和底部支撑接触区域的最大应力进行计算，从而最终确定管垛允许堆放层数，该方法可以对外部涂层为防腐涂层和水泥配重涂层的情况进行计算。

对于管垛堆放层数设计，为保证安全，可以根据不同工况选取合适的安全系数进行堆放层数计算，同时还应考虑管垛边挡高度及强度，存储场地面强度，船舶甲板强度及船舶运输的稳定性，本文并未涉及，管垛堆放层数应取所有限制条件下的最小值。

除此以外，针对钢管涂层为多层结构的管道堆放层数计算，还应对于管道内部各层的应力进行计算，针对管道内部各层的应力是一个极其复杂的计算过程，本文不做介绍。推荐采用有限元方法，建立合理的三维有限元模型进行计算分析，可以校核管道钢管层、配重层、防腐层、夹克层及保温层强度，以得到合理的管垛允许堆放层数[5]。