抽油机故障诊断的分布驱动主动学习算法

汪 敏，周 磊，闵 帆，张 响，沈佳园，韩 菲

（1.西南石油大学电气信息学院，成都 610500；2.西南石油大学计算机科学学院，成都 610500；3.浙江浙能天然气运行有限公司，杭州 310052；4.新疆油田公司风城油田，克拉玛依 834000）

抽油机井一直都是石油开采中的重要组成部分，为了更好地了解抽油机井的工作状况，就必须对其工作时产生的一系列数据进行分析，从而判断抽油机井是否正常工作。通过测量抽油机往复一周所产生的载荷、位移系列数据来绘制地面示功图［1］，由不同因素导致的抽油机故障会形成不同形状的示功图。及时准确地对示功图进行诊断，得出抽油机的故障原因，可以减少财产损失和延长零部件的使用寿命。目前以示功图为研究对象对抽油机进行故障诊断是最常见的方法。常见的有BP神经网络［2］、主成分分析方法［3］以及支持向量机（Support vector machine，SVM）［4］等。田增国等［5］提出了一种基于主成分分析的示功图故障诊断系统。该方法是利用降维技术保留大量信息的情况下将原始数据进行压缩，将大量的线性相关属性变量转化成几个相互独立或者不相关的变量。通过计算示功图经过主成分分析后的数据之间的相关系数来判定不同故障。施海青等［6］提出了一种基于支持向量机的抽油机故障诊断方法。该方法采用矢量曲线对数据进行压缩，从而提取井下示功图特征点。采用“一对一”的方式构建多分类支持向量机分类器，能够对多个故障做出识别。杜娟等［7］提出了一种基于卷积神经网络的抽油机工况识别方法。该方法在原有神经网络基础上增添了两个注意力机制模块，能够很好地调节原有模型的过拟合情况，使模型更能关注小类别工况。在工况复杂的抽油机故障诊断实验中，该模型具有良好的泛化能力。文献［8］提出了一种基于稀疏多图正则化极限学习机的抽油机故障诊断方法。该方法通过快速离散曲波变换提取示功图特征，利用图表示学习方法构建类内图和类间图来表示同类数据间的关系以及不同类别数据间的关系。通过稀疏表示，可以使同一类数据的结果输出尽可能相同，不同类别的数据的结果输出尽可能分开。示功图故障诊断测试表明，该模型在抽油机工况识别上有很好的表现。文献［9］采用了适应噪声因子的滤波器以及使用基函数来与之结合的方法。使用近似多边形的傅里叶描述符方法来提取示功图特征，采用径向基函数（Radial basis function，RBF）神经网络，利用指标图数据和生产数据建立故障诊断模型，使用自适应噪声因子来解决模型中的自适应滤波问题。实验表明，模型在示功图故障诊断方面取得不错的表现。

现阶段常用深度学习方法进行故障诊断测试，Peng 等［10］开发了一种新型双向门控循环单元（Bidirectional gated recurrent unit，BGRU），在训练阶段对每个训练样本进行加权，以减少类不平衡的影响，然后利用成本敏感的主动学习来选择候选样本。在实际等离子体蚀刻工艺数据集上评估了所提出方法的有效性。Jin 等［11］提出一种用于复合故障诊断的新型解耦注意力残差网络，应用在轴承数据集，获得了优越的精度，大大减少了领域专家的标记工作量。Zhang 等［12］引入概率主动支持向量机（Probabilistic active support vector machine，Pro-ASVM）的学习方法，根据样本点的概率选择点作为支持向量。应用于轴承振动信号的分类，获得了优异的分类效果。Jian 等［13］针对实际工业故障诊断训练集规模较小的问题，提出了一种基于主动和半监督学习的故障诊断新方法。应用于实际的智能维护系统数据，为小训练集下的故障诊断提供了一种有前途且有用的方法。Chen 等［14］针对自组织蜂窝网络（Self-organizing cellular networks，SONs）中的故障诊断的多分类问题，提出了一种新的基于主动学习的故障诊断方案。该方案只需很少的标记训练实例即可实现高诊断性能，从而显著降低成本。Punčochář 等［15］提出了主动故障诊断（Active fault diagnosis，AFD）领域的基本分类方法。由于实际油田生产过程中存在抽油机井下的故障种类数量多且不同故障类别的数据量不平衡、人为标注的样本少且费时费力等问题，常用的深度学习工况识别模型难以在实际工作中落地。同时，主成分分析方法、支持向量机等传统的方法无法很好的处理不平衡数据分类问题。针对以上方法存在的不足，本文提出一种基于分布驱动的多类别长尾数据代价敏感主动学习算法（Cost-sensitive active learning algorithm based on distribution-driven multi-class long-tailed data，CALA）来解决这一困难且非常有意义的问题。

1 特征提取

本节主要介绍本文示功图的特征提取方法，结合灰度矩阵的知识，提取示功图灰度矩阵的6 个特征作为统计特征。

1.1 网格法提取灰度矩阵

本文采用网格法［16］对示功图进行灰度矩阵提取，网格法构建示功图的灰度矩阵主要包含如下步骤：

（1）标准化示功图

为了更好地比较不同工况下的抽油机示功图，消除示功图量纲对收集到的数据的影响，将采集到的示功图数据进行标准归一化。为符合石油工业的习惯，将示功图放进一个长宽比为2∶1 的矩形中，满足绘制的地面示功图被矩形内切这一条件。

（2）网格化示功图

将长方形分成多个网格，本文将之划分为20×10 大小的网格个数，并将所有网格的初始灰度赋值“0”；若网格内含有示功图曲线，其灰度值赋值为“1”；边界内部网格的灰度值往矩形中心依次递增；边界外部网格的灰度值以矩形边界依次递减。边界搜索方式按列进行。

1.2 特征向量提取

通过对构建好的示功图灰度矩阵［17］进行数理统计，计算灰度均值gˉ、方差σ2、偏度ε、峰度P、能量E和熵ξ这6 个统计特征作为示功图特征值。

假设灰度矩阵大小为G(A，B)，矩阵中任意位置的值gab(1 ≤a≤A，1 ≤b≤B)表示示功图网格化后对应位置的灰度。设灰度矩阵中灰度级数为R，设某一灰度级数r的数量为T(r)，则该灰度级数在灰度矩阵中出现的概率可表示为p(r)=T(r)/(A×B)。

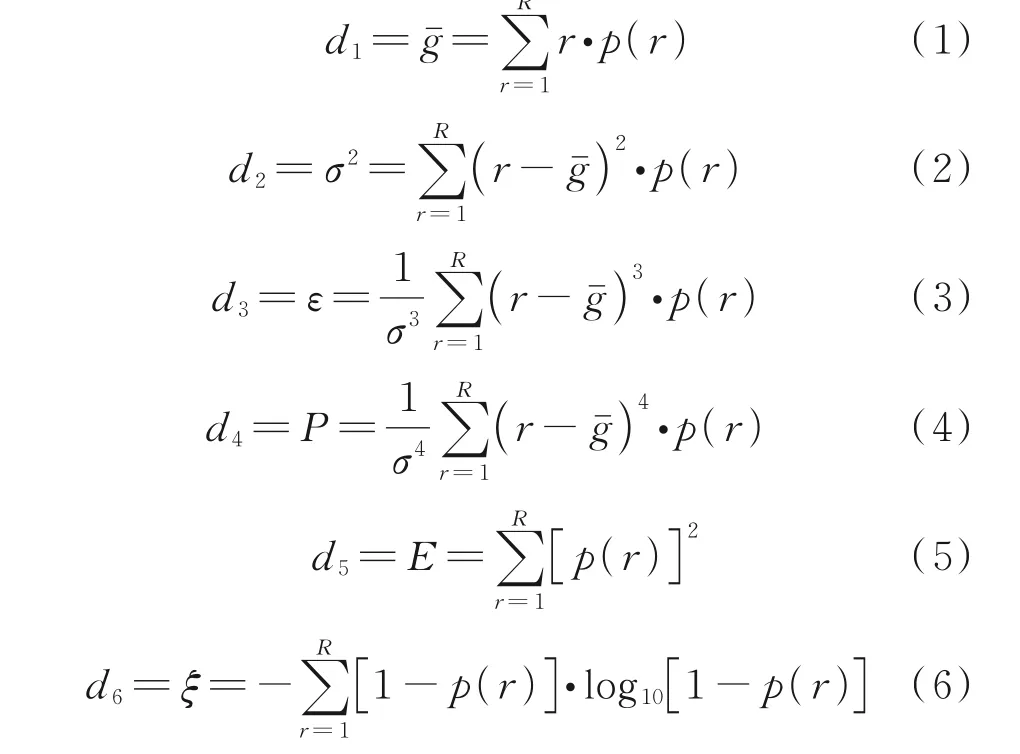
以统计的6 个特征值{d1，d2，d3，d4，d5，d6}作为最终的分类特征向量。

2 算法设计

本文的数据模型是教师和误分类代价决策系统（TMC-DS）［18］，该决策系统定义成1 个四元组

式中：X代表一个数据集向量；y代表数据真实标签向量；M代表误分类代价矩阵；t代表专家代价为1。CALA 算法过程框图如图1 所示。

图1 CALA 算法流程框图Fig.1 CALA algorithm flow chart

2.1 获取数据最佳分布

本节设计了一种基于误差统计函数探索数据最佳聚类簇数的方法。依据“物以类聚”的原则，样本间距离越接近，它们的标签就越可能一致的假设［19］。通过对多个结构化数据集进行分析测验，得到拟合误差曲线。其具体步骤如下：

（1）距离阈值实例对

依据距离阈值λ的相邻实例对(xi，xj)定义为

式中：dist(xi，xj)代表数据样本xi和xj间的欧式距离；λ为设定归一化距离阈值；Nλ为满足条件的实例对个数。

（2）实例对标签统计误差

根据式（8）得到的实例对个数，依据不同的距离阈值定义实例对标签统计误差函数

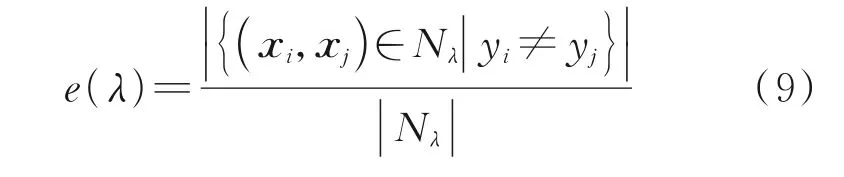
式中：|Nλ|为满足阈值λ下实例对数量；yi和yj为样本xi和xj对应的真实标签。

（3）获取经验误差函数

首先选取30 个不同样本个数，不同特征个数以及不同类别数量的公开数据集，其次通过式（8）计算不同阈值λ下的实例对个数，然后通过式（9）统计不同阈值λ 下的标签统计误差e(λ)，最后通过多项式拟合得到经验误差函数，即

拟合曲线相关系数达到0.999 9，符合工程实际。

（4）优化目标函数

式中：n为数据样本总数，ni为对应第i簇的样本个数，λi为第i簇的最远两样本距离与数据集最远两样本距离的比值。

2.2 预分类

利用预分类修正基于统计策略得到的最佳簇数。将统计策略得到的最佳聚类簇数中每一簇通过主动学习方法［20］选择最具代表性的样本作为训练集，通过概率预测模型得到样本预分类标签。训练集的选取方式为

式中：ci为第Ci簇的聚类中心；s*为该簇交由专家标注的样本。

通过Softmax 回归［21］，输入任意样本xi，属于样本对应的预测概率为

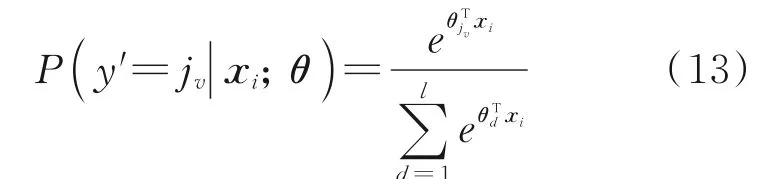
其预测标签为

式中：l为样本类别数量；θ为Softmax 目标函数训练得到的最佳参数。通常通过梯度下降法［22］求解。

2.3 更新最佳聚类分布

通过Softmax 回归模型进行预分类，测试样本会得到一个相应的预测标签。将数据再次进行聚类，依照得到的样本预测标签和经验误差曲线构建新的聚类优化目标函数，有

式中：∂1和∂2为权重系数；pu(Ci)为第Ci簇的预测标签纯度，定义如下

2.4 集成分类

根据找到的最佳聚类簇数，将数据进行聚类，选取每一簇离中心点最近的样本作为训练集，通过Softmax 回归得到测试集的预测标签。并且将该训练集同时作为K最近邻算法（K-nearest neighbor，KNN）预测分类模型的训练集，得到测试集的KNN 预测标签集合j'。结合二者的预测标签构建决策函数

2.5 伪代码及时间复杂度分析

（1）算法伪代码

算法 CALA

输入决策信息系统S=(X，y，M，t)

输出预测标签集合Y=[y]n×1

步骤1～5 为赋值和通过聚类得到数据初始分布信息阶段，计算量主要在于聚类算法，时间复杂度为O(kdn)。步骤6～8 为选取训练样本和Softmax 预分类过程，选取训练样本阶段时间复杂度为O(n2)，Softmax 预分类过程时间复杂度为O(n'2)，n'为预分类样本数量，为原始样本总数减去训练样本后的样本个数。n'＜n，这阶段总的时间复杂度为O(n2)+O(n'2)=O(n2)。步骤9～25 为更新最佳聚类分布和集成分类过程，更新最佳聚类分布与初始聚类阶段时间复杂度一致为O(kdn)，集成分类过程中，Softmax 分类阶段时间复杂度为O(n2)，KNN 分类阶段时间复杂度为O(n)，考虑while 循环过程，则这阶段总的时间复杂度为O（kdn·log2n）+O（n2log2n）+O（nlog2）=O（n2log2n）。其中特征数d＜n，聚类簇数k＜n，时间复杂度为

O(kdn)+O(n2)+O(n2log2n)=O(n2log2n)。

3 算法验证

3.1 数据集描述

实验采用来自新疆风城油田4 个作业区不同抽油机示功图数据对本文算法进行验证分析。其具体信息如表1 所示。这些数据包含多个类别且都是不平衡数据。其中A01 是抽油机作业一区常规油井采集的示功图数据，A02 是抽油机作业二区稠油油井采集的示功图数据，A03 是抽油机作业三区超稠油油井采集的示功图数据，A04 是抽油机作业四区SAGD 油井采集的示功图数据。4 个油田示功图数据包含有正常工作、供液不足、气体影响、气锁、上碰泵、下碰泵、游动阀关闭迟缓、柱塞脱出泵工作筒、游动阀漏、固定阀漏、砂影响+供液不足和惯性影响这12 种常见抽油机工况。其中，大部分为正常工作，气体影响工况为最小类别故障工况。A01 中正常工况样本有4 474 个，气体影响工况有300 个，不平衡比例为14.91；A02 中正常工况样本有4 974 个，气体影响工况有300 个，不平衡比例为16.58；A03 中正常工况样本有5 374 个，气体影响工况有300 个，不平衡比例为17.91；A04 中正常工况样本有5 845 个，气体影响工况样本有300个，不平衡比例为19.48。实际油田工作环境下，抽油机示功图中气体影响这一类工况数据稀少。当发生气体影响时，抽油机泵腔内压力不能正常下降，使得加载速度变慢，采油效率降低。对小类别工况进行准确识别能够及时对故障机械进行维修，减少损失、延长机器设备的使用寿命。

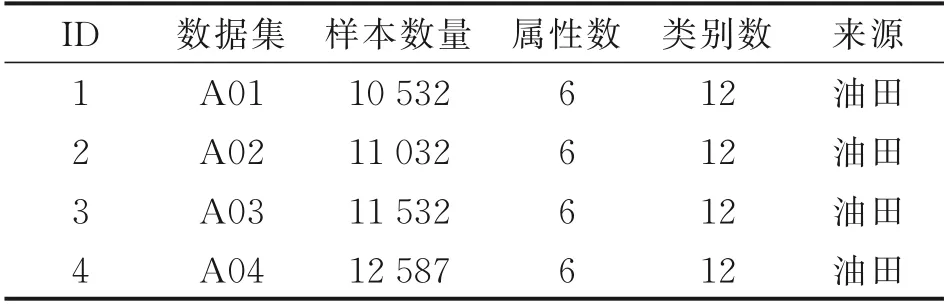
表1 数据集信息Table 1 Information of datasets

3.2 评价指标

本文实验采用精度、平均代价F-Measure 作为评估算法性能的指标，其精度定义为

式中：|Xt|为测试集的样本数量，error 为误分类样本数量。

对于不平衡抽油机故障工况数据而言，刻画不同工况具有不同的误分类代价是很有必要的。对于稀少工况类别数据在实际场景下样本数稀少，误分类的代价应远大于常见工况类别数据误分类代价。本文设定的代价矩阵［23］为

式中：ni和nj分别表示测试集中属于第i类和第j类的样本数量。平均代价为

式中：Aij为将第i类误分类为第j类的样本数量；|Xr|为交由专家标注的样本个数；t为查询标签代价，实验中设置为1。

为验证模型在不平衡数据分类上的性能，从准确率（Precision）和召回率（Recall）和F-measure 分数［24］这3 个评价指标对模型性能进行综合评判。这3 种评价指标可以由表2 的混淆矩阵计算得出。

式中：TP 和TN 分别表示真实标签与预测标签全部为正，全部为负的样本数量；FP 表示真实标签为负，预测标签为正的样本数量，而FN 相反。准确率是针对模型测试结果，表示预测为正实例中有多少真正的正实例；召回率是针对于原始样本具体标签，表示原始样本的正实例有多少被模型预测正确。F-measure 综合兼顾这两个评判标注，是评价算法性能最常用的指标。

表2 混淆矩阵Table 2 Confusion matrix

3.3 实验设计

为验证提出的算法模型性能的优越性，将本文提出的CALA 算法与基于欠采样技术的代价敏感学习算法（Under-sampling，US）［25］、基于阈值移动调整类别阈值算法（Threshold-moving，TM）［26］、基于过采样技术的代价敏感学习算法（Over-sampling，OS）［27］、增强的自动双支持向量机算法（Enhanced automatic twin support vector machine，EATWSVM）［28］、基于边距的非定性采样主动学习算法（Uncertainty sampling with margin，UM）［29］、基于熵的不确定性采样主动学习算法（Uncertainty sampling with entropy，UE）［30］和基于成本嵌入的主动学习算法（Active learning with cost embedding，ALCE）［31］以及卷积神经网络（Convolutional neural network，CNN）这8 种算法进行比较。US、TM、OS 和EATWSVM 是4 种代价敏感不平衡数据处理方法，UM、UE 和ALCE 是3 种代价敏感主动学习算法。

4 实验结果及分析

4.1 与代价敏感不平衡数据处理方法比较

本节实验中，将真实采集到的4 个油田的抽油机示功图数据用于模型性能验证。每个数据集选取30%的样本交由专家标注标签进行模型训练，其余样本作为测试集。同样条件下，随机10 次重复实验，统计各评价指标结果。结果取均值和标准差如表3 所示。

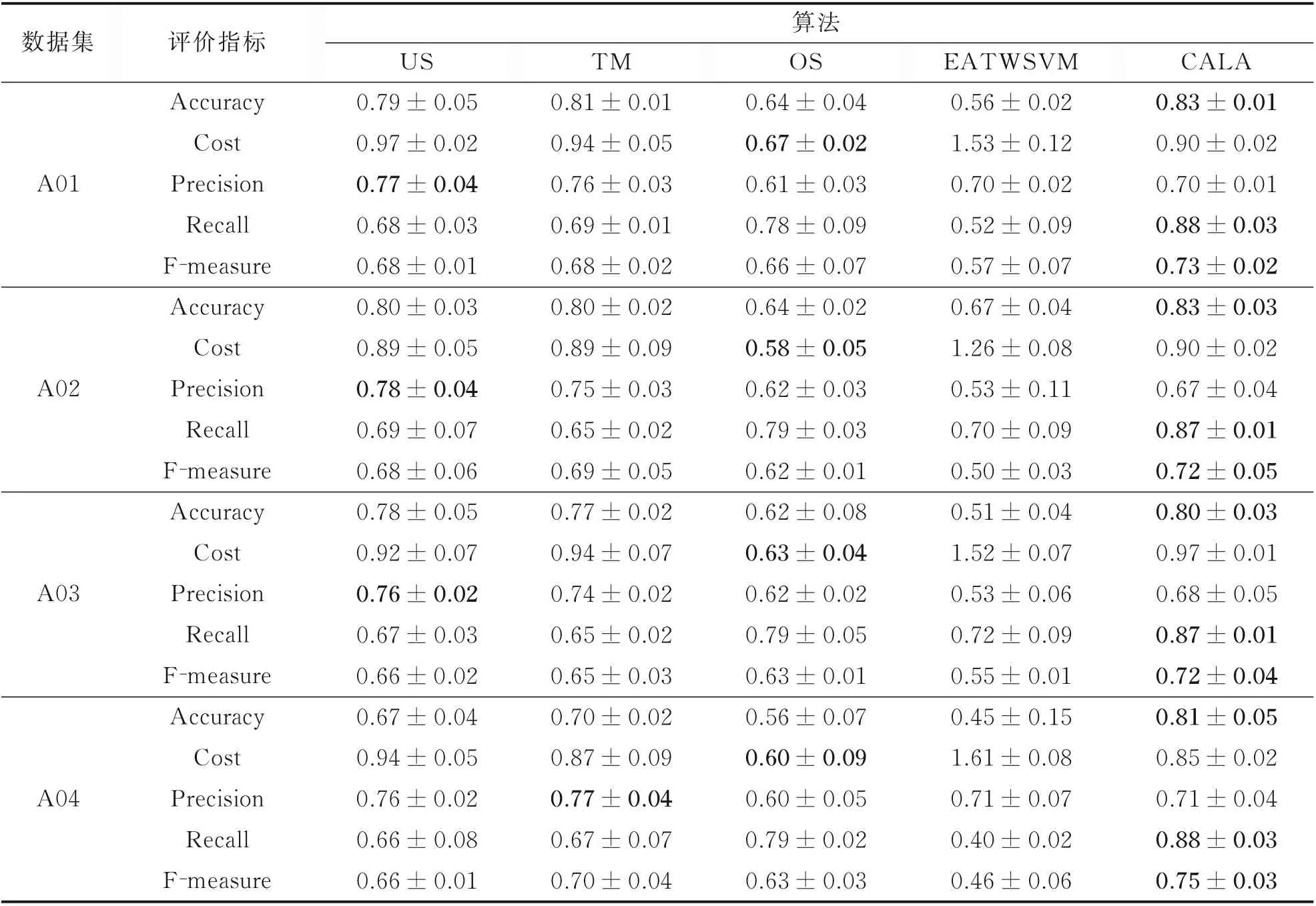
表3 与代价敏感不平衡数据处理方法对比实验结果(均值±方差)Table 3 Comparison of experimental results with cost‑sensitive imbalanced data processing methods(mean±std)

从表3 可以看出，在A01、A02、A03 和A04 数据集中，本文所提出的CALA 算法在精度、召回率和F-measure 这3 种评价指标上展现的性能都优于其余4 种对比算法。在代价性能测试上，过采样算法OS 表现最好，CALA 在4 个数据集上的代价排名分别为第二、第四、第四和第二。

为验证本文提出的CALA 算法在不同查询比率下的性能，图2 显示了CALA 与4 种代价敏感不平衡数据处理方法在查询比率为30%、35%、40%、45%和50%下的F-measure 对比，对于4 个真实油井数据集，CALA 算法的平均F-measure 明显高于其余算法。

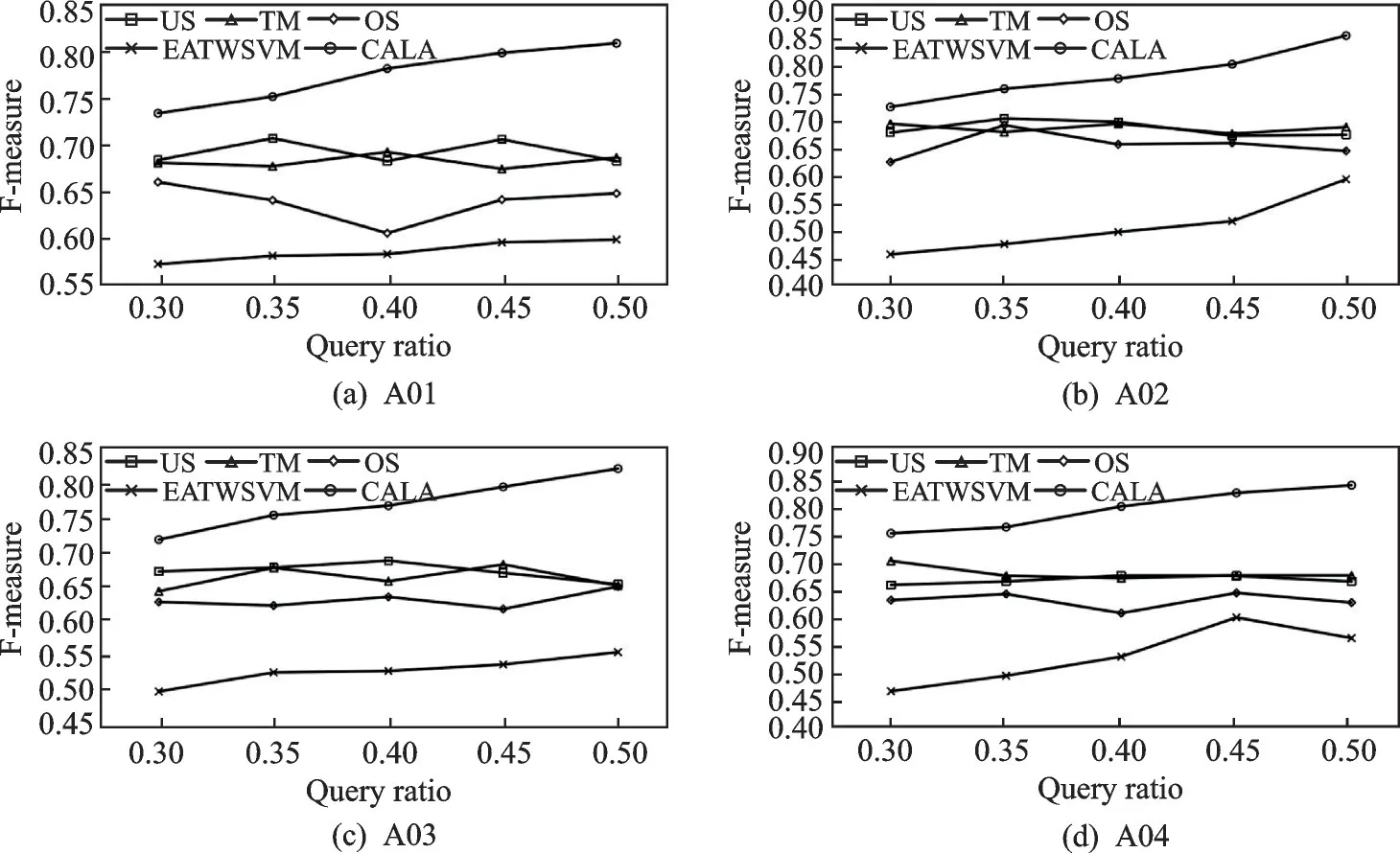
图2 CALA 算法与4 种不平衡数据处理算法在不同查询比率下的F-measure 比较Fig.2 Comparison of F-measure between CALA algorithm and four imbalanced data processing algorithms under different query ratios

4.2 与代价敏感主动学习算法比较

本节实验中，将真实采集到的4个油田的抽油机示功图数据用于模型性能验证。每个数据集选取30%的样本交由专家标注标签进行模型训练，其余样本作为测试集。同样条件下，随机10次重复实验，统计各评价指标结果。结果取均值和标准差如表4所示。

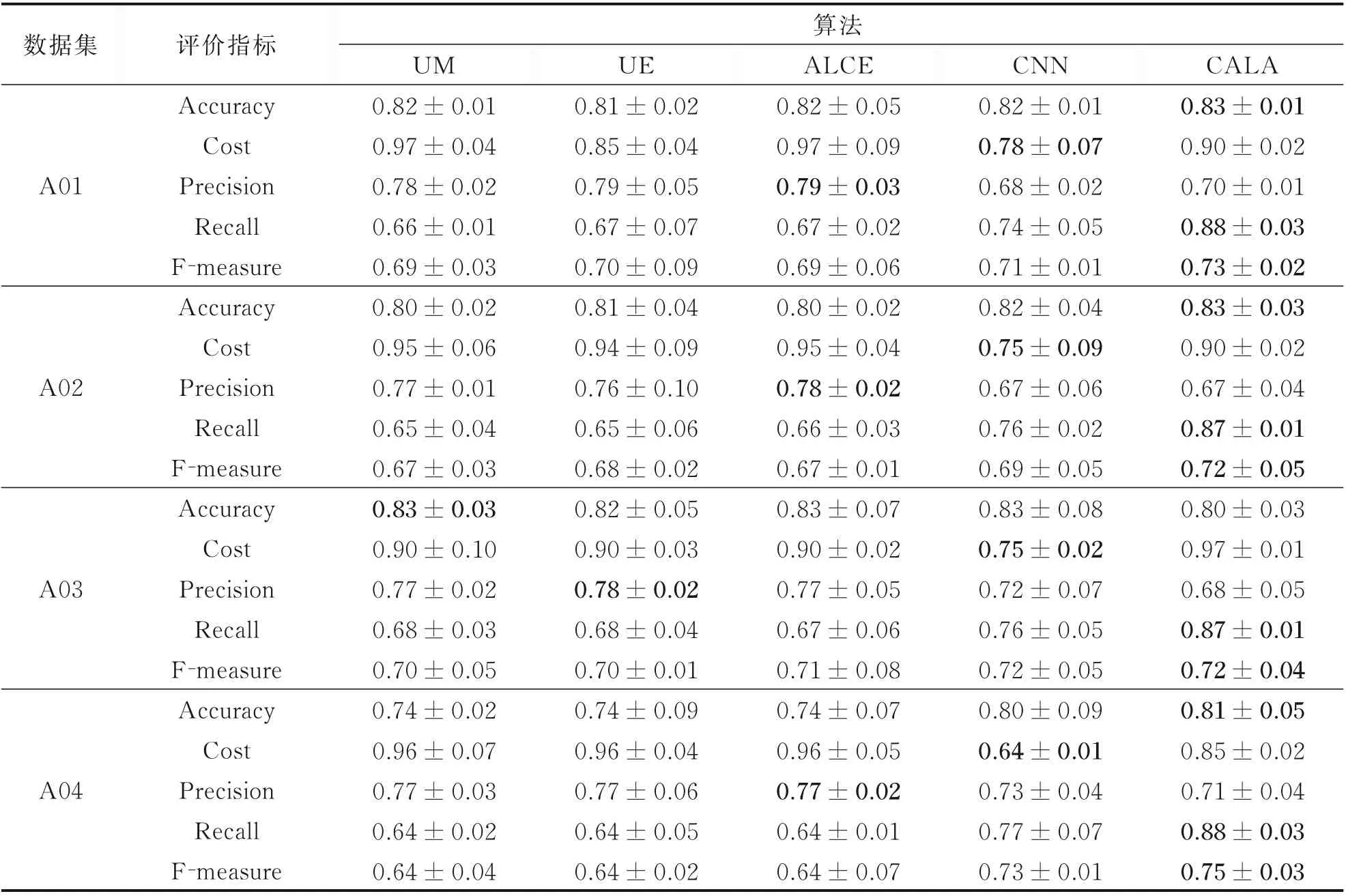
表4 与代价敏感主动学习算法对比实验结果(均值±方差)Table 4 Comparison of experimental results with cost sensitive active learning algorithms(mean±std)

从表4 可以看出，在A01、A02 和A04 数据集中，本文所提出的CALA 算法在精度、召回率和F-measure 这3 种评价指标上展现的性能都优于其余4 种对比算法。A03 数据集上，提出的CALA 算法在召回率和F-measure 评价上优于其余对比算法。在代价性能测试上，深度学习算法CNN 表现最好，CALA 在4 个数据集上的代价排名分别为第三、第二、第五和第二。

为验证算法在不同查询比率下的性能，图3 分别显示了与3 种代价敏感主动学习算法以及深度学习算法在查询比率为30%、35%、40%、45%和50%下的F-measure 对比，对于4 个真实油井数据集，CALA 算法的平均F-measure 明显高于其余算法。

图3 CALA 算法与代价敏感主动学习算法以及CNN 算法在不同查询比率下的F-measure 比较Fig.3 Comparison of F-measure between CALA algorithm and cost-sensitive active learning algorithm and CNN algoithm under different query ratios

4.3 小类别工况下的模型性能测试

为验证本文算法在小类别上的识别性能，气体影响工况为最小类别工况。其中A01、A02、A03和A04 数据集中气体影响工况占比分别为2.85%、2.72%、2.60% 和2.38%。表5 和表6 分别列出CALA 算法和8 种对比算法在气体影响工况上的性能。表5 和表6 可以得出，CALA 算法在小类别识别方面的准确度和F-Measure 优于其余对比算法；在召回率方面，US、TM 和UM 算法表现较好。

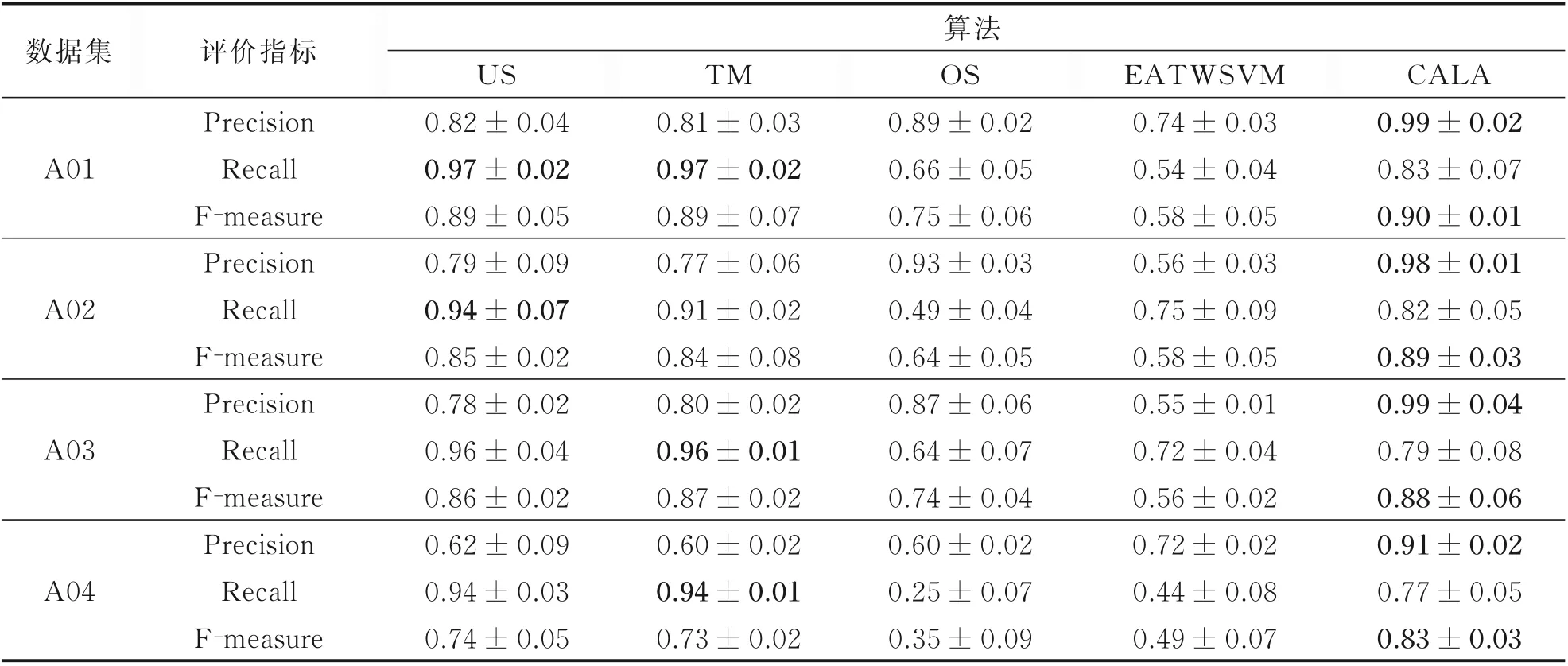
表5 小类别工况下与代价敏感不平衡数据处理方法的对比实验结果（均值±方差）Table 5 Experimental results compared with cost‑sensitive imbalanced data processing methods under small category conditions(mean±std)

4.4 模型变换测试

本文算法的核心在于提出的主动查询策略以及基于代价优化目标实现分布优化。因此，本文将KNN 算法替换成朴素贝叶斯（Naïve Bayes，NB）算法即CALA_NB。表7 为CALA_NB 在查询比率为30%下重复10 次实验得到的结果。结果表明，将KNN 替换成NB 之后，算法的效果相差不大，说明本文算法性能适用性能较好。

表6 小类别工况下与代价敏感主动学习算法的对比实验结果（均值±方差）Table 6 Experimental results compared with cost‑sensitive active learning algorithms under small category conditions(mean±std)

4.5 算法适用性分析

为验证算法在12 种常见抽油机工况下的不同性能，图4 分别显示了CALA 在A01、A02、A03 以及A04 四个数据集用30%查询比例情况下12 种工况的精度。其中横坐标1～12 分别对应12 种抽油机工况。从图中可以看出CALA 在各种工况下的识别精度表现都较好。

4.6 模型时间开销对比测试

表8 为本文提出算法CALA 与其余9 种模型在4 个实际抽油机数据集上运行的时间开销。本文提出的算法CALA 均排名第4，由于使用了集成好的US、TM 和OS 算法，这3 种算法运行速度更快。

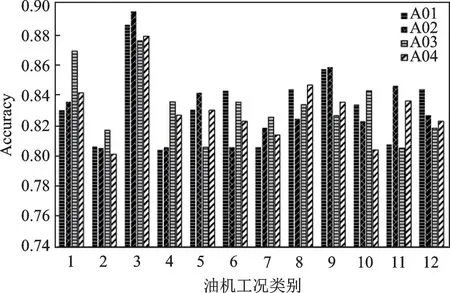
图4 CALA 算法在4 个油田数据集上的12 种工况精度Fig.4 Accuracy of CALA algorithm for 12 working conditions on four oil field datasets

5 结论

针对抽油机井下工况复杂、种类繁多的特点，本文提出一种抽油机故障诊断的分布驱动主动学习算法。该算法首先利用大量结构化数据构造经验误差函数，结合主动学习查询少量关键样本，通过代价敏感方法优化算法模型，得到工况数据最佳聚类簇数来改善数据分布。有效利用迭代过程中的代价优化函数，使得该算法在抽油机示功图故障诊断方面较对比算法在精度上有较大提高。在小类别工况识别中，本文提出的算法在准确度和F-measure 分数上明显优于其余对比算法。针对实际工程环境下未知工况的识别和诊断是下一步将要研究的内容。