读懂教材内容的实质与逻辑

刘晓婷

【摘   要】教材是教师进行教学的重要资源，备教材是教学的重要环节。但当前教学中仍存在忽视教材的现象。从一道“扣分”测试题带来的困惑出发，通过调研了解到教师在分数乘分数（分数除以整数）图式表征中的理解失之偏颇，回归教材分析背后的原因，提出读懂教材内容实质与逻辑的三个角度：审慎眼光思教材、进阶视野观教材、动态视角析教材。

【關键词】教材内容理解;分数乘分数;分数除以整数

教材是教师进行教学的重要资源，是教学活动设计的蓝本。教师在备课过程中，对教材进行细致的分析、梳理是非常重要的环节，是制订教学目标、把握教学重难点、设计教学活动及选择教学策略的重要依据之一。然而教师对教材作用的忽视，导致教学中存在一些问题。例如，在展示课或比赛课中，为了凸显教学的创新性，教师对教材弃置不用，进行“随意的创造”;在日常教学中，“机械”使用教材，忽视学生的困难等。在当前“双减”核心任务下，反观这些现象，亟待一线教师回归对教材进行解读，重视对数学教材的分析，深度理解教材中的教学内容，设计有效的教学活动，提升课堂教学质量。下面，从一道“扣分”测评题带来的困惑谈起，追寻其背后的根源，简析读教材的视角。

一、研究缘起：一道“扣分”测试题带来的困惑

某区六年级期末测试中有一道题目，“画图表示‘5/6÷ 3’的过程和结果”。某生作答情况如图1所示，在判卷时教师扣掉了学生的一半分。

判卷教师给出的扣分理由是“学生没有标注数据”，但学生认为“本题要求画图表示，并未对标数据做要求”。暂且不考虑题目表述严谨性的问题，“5/6÷3”究竟应该如何画图表示呢？学生画的图有问题吗？如果有，问题是什么？笔者把题目稍作调整后，对19位教龄为5～10年的优秀青年教师进行调研，请他们“画图表示‘5/6×1/3’的过程和结果”，得到六种主要类别的图式。之后以投票的形式，对90位在职小学数学教师进行调研，让教师选出赞同的图式，结果如表1所示。

由上表可见，六个图式全部有人支持。其中图式⑥的支持率最高，约为65.60%，图式⑤的支持率最低，约为18.90%。图式②和学生作答示例（如图1）相同，支持率约为45.60%。这一调研结果说明了什么，能带给我们怎样的启示呢？

二、追本溯源：调研数据引发的问题与思索

上述案例引发如下问题：第一，哪种图式能更准确地表示“5/6×1/3”的过程和结果？如何用图式准确、恰当地表示分数乘分数（分数除以整数）的计算过程？第二，为何教师在画图时会有如此多样的表达？其根源是什么？笔者结合文献研读、教材梳理、教师访谈等方式，作如下阐释。

（一）图式分辨：紧扣运算意义，直观精准地表达计算过程

对比表1中的六个图式，有如下区别：其一，图式①和③没有体现出计算的过程，图式②④⑤⑥给出了计算过程，部分图式过程很完整。其二，图式①内部线全部为虚线，其他几个图式内部大多为实线，其中图式⑥最右侧空白位置为虚线。其三，图式④⑤⑥在第三步“分成三份”时，分割线均未延长，而图式②的第二步分成三份时，分割线直通最右侧，图式①③类似。其四，图式⑤平均分成6份的方式与其他图式不同，采用了横纵切割法，同时还把5/6转为化“1/6×5”，步骤较多。其他图式平均分成6份时，采用纵向切割法，平均分成3份时采用横向切割法。

不同图式之间的差别进一步聚焦到三个问题：（1）把一个长（正）方形平均分成6份，取其中的5份，老师们没有异议。分歧在于接下来分的3份，分的对象是谁。（2）把一个长（正）方形进行分割时，用实线还是用虚线，还是虚实线结合？其中的道理是什么？（3）画图表示方式是否只有一种？

不论是“5/6×1/3”，还是“5/6÷3”，其意义均可解释为“把5/6平均分成3份，求其中的1份”，即分成3份的对象应该是5/6，图式④⑥都清晰地表示了这一意思。但分完3份并取出其中的1份后，这时的1份究竟是多少，还需要明晰其与单位“1”的关系，图式⑥的最后一步，把分割线进行延长后，可以清晰地看到这部分是单位“1”的5/18。按此解释，图式⑥准确表示了算式和结果的意义。其中虚线的使用是为了更好地区别分割和确认结果两个部分，能够让别人看清思考的过程。此外，图式⑤做了转化，虽然分割方法较复杂，但还是准确表征了所给出的算式的意义。

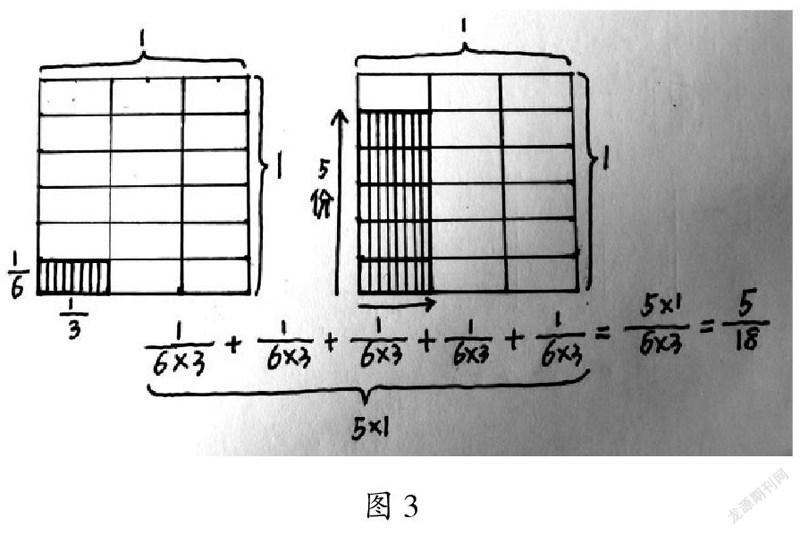
分数乘分数的意义还可有另外一种解释，数学家伍洪熙把边长等于m/n和k/l（这里的n，l都是非零自然数）的矩形称为边长为m/n和k/l的矩形，并由此定义分数乘法：m/n×k/l=边长为m/n和k/l的矩形的面积。对于任意自然数l>0，n>0，有1/n×1/l=1/nl，如图2（左）所示。对于任意分数m/n和k/l，一般乘积公式m/n×k/l=mk/nl成立。此时把m/n看成由m条长为1/n的线段拼接而成，k/l看成由k条长为1/l的线段拼接而成。如图2（右）所示，大矩形恰好是由m/k个这样全等的小矩形拼接而成，其面积等于1/nl+1/nl+…+1/nl=mk/nl[1]。

表1中的图式③貌似和图2有相似之处，但仔细分析还是有差别。图2中使用的是矩形的面积来定义分数乘法，是把单位正方形进行分割，以5/6×1/3为例，1/6×1/3是基于定义得到的，定义及运算规则有严格的推导过程，计算过程用图3表示。而表1图式中老师们的想法是基于“某物的m/n”这一定义，即m/n×k/l=分数m/n的k/l。在表1所示的图式中，都是用长方形代表单位“1”，先表示出5/6，再来表示5/6的1/3。

（二）根源初探：读教材浅尝辄止导致理解失之偏颇

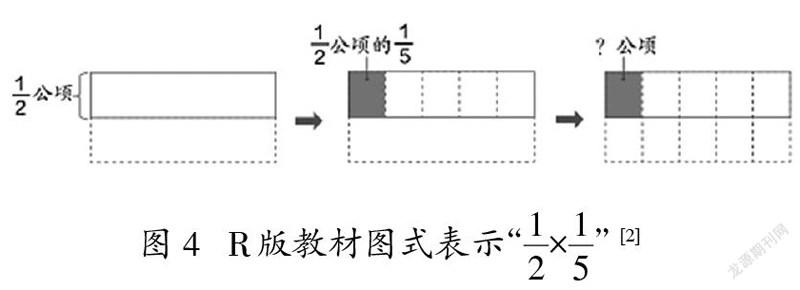
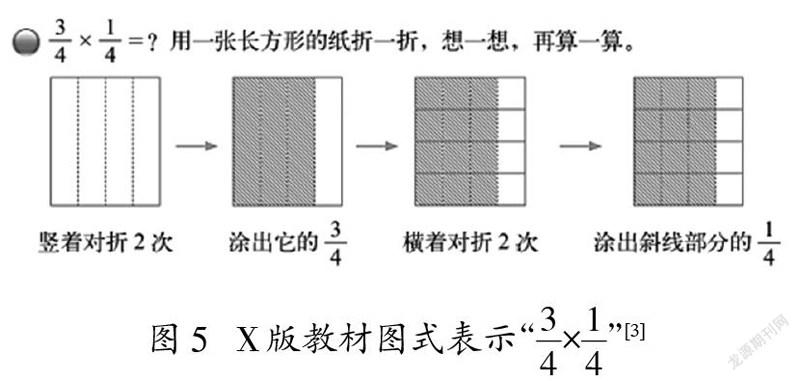
为何老师们在画图时会出现如此多的样态呢？通过访谈了解到，这与教师对教材的认知有关。以R、X、C三个版本的教材为例，三个不同版本的教材在用图解释分数乘分数时存在差异，如图4～6。

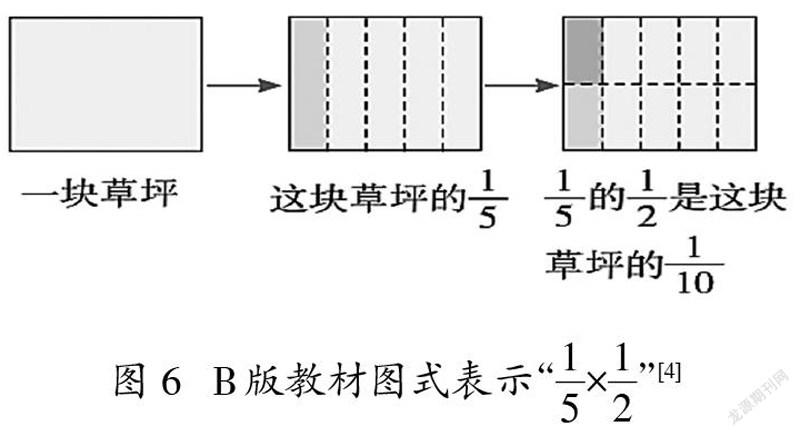
三个版本教材在用图式表示分数乘分数时全部给出了计算过程图。表示第一个因数时基本相似，只有R版教材用虚线表示了单位“1”的另一部分。差异最大部分仍是m/n的k/l的表示方法，R版教材先把1/2平均分成5份，得到1/2的1/5，之后再用虚线延长分割线，得到10个格子，1/2的1/5正好是10个格子中的1个，即为1/10。X版教材以“折”表示分割，得到3/4后再“横着对折两次”，但此时的“对折”直观呈现的是平均分整个长方形（B版教材一条虚线横穿长方形），从平均分的对象上来看，容易造成误解。用图式表征，其目的是帮助学生直观理解学习内容，理解计算结果的合理性，教师需要明辨图式的准确性、适宜性。

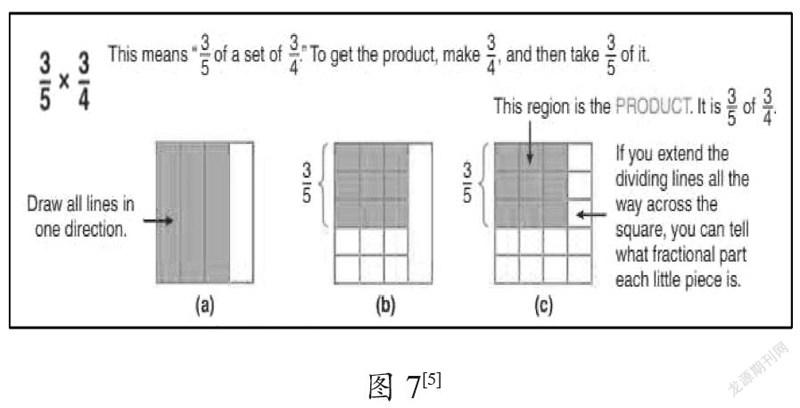
参阅其他教材和教学资料，关于分数乘分数的图式表示方法，有些方式值得借鉴。如图7（c），就标注了延长线的意义，即“把分割线延长至正方形，就能知道代表每一小块儿的分数是多少”。

在讨论“分数乘分数”的图式时，有教师认为图式⑥过于烦琐，认为如图式②所示，两步足够，并给出了“证据”——R版教材在图式表示分数除以整数时就只画了两步（如图8）。对该教师的质疑如何回应呢？笔者以为，教师应当关注教材内容呈现的进阶。分数乘分数在分数除以整数之前，R版教材两幅图的差异也恰好表明了教材在设计呈现内容时考虑到了儿童数学学习的经验，在分数乘分数图形表征学习的基础上，分数除以整数图式可以做适当的删减，而在关键部分，教材还是进行了巧妙且精准的表达，在把4/5平均分成两份时，前面仍用实线表示分的对象是4/5，后面用虚线延长确认每个小格的分数值。但遗憾的是，教材编写者的编写意图被部分教师忽视了。

此外，在对19位教师的调研中，仅有一位教师画出了图式⑤，该种画法在调研中的支持率仅为18.90%，这同样与教材呈现有关。仍以上述三个版本教材为例，分数乘分数及分数除以整数的图式，教材多采用的是先纵向分割，后横向分割的方式，教师习惯于这些图式后，形成了思维定式，对其他图式的分辨能力有所下降。三个版本教材中只有B版教材的分数除以整数图式表示给出了不一样的形式（如图9）。在第一步表示出9/10后，再思考9/10的1/3是多少，此时直接横向分割可以得到结果，但由于数的特点，不分割也很容易把9/10分成三部分，每份是3个竖条，即为3/10。这样的思考既体现了对学生数感和观察能力的培养，也让学生知道学习不要被模式所限制，灵活处理问题很重要。

反观期末测试中那道被“扣分”的题目，学生回答时是否标注了数据并不是最要紧的问题，要紧的是那样的图式表征真的准确、恰当表明5/6÷3”的过程和结果了吗？透过学生的回答，教师应反思之前是如何教學的，是否真的给学生理解分数运算提供了有效支持，用怎样的题目能更好地考查学生对分数运算的理解，等等。

三、延伸思考：多维视角读教材，明晰教学内容的实质与逻辑

基于上述案例及分析过程，对教材研读和使用有如下思考。

（一）审慎的眼光思教材，明晰教学内容实质

教材是教学的蓝本，教师在研读教材时需要有审慎的眼光。弃置不用不可取，全盘接受不适当。案例中呈现的三个版本教材，有些对m/n的k/l的表示方法稍欠妥当。教师应结合学生的学情对教材内容进行审视，用问题驱动自我思考，“这里的表示学生能懂吗”“学生都会这样想吗”，等等。教材是以文本的形式承载编者的思想和意图的。教师在进行课堂教学设计时，要与教材进行“对话和交流”，从而把握教学内容的实质。教师应以审慎的眼光分析和思考教材，将静态的教材内容转化为动态的学习活动。

（二）进阶的视野观教材，厘清教学内容逻辑

教材在编排教学内容时是有逻辑的，教师应以进阶的视野看教材，明晰相关内容之间的联系。上述案例中，分数乘分数和分数除以整数在意义上具有一致性，R版教材在处理直观图式时就考虑到了内容的关联性，在图式呈现方式上有所变化，体现了内容及思维的进阶。数学教材中的诸多内容存在着紧密的联系，前面内容的教学应为后续内容的学习积累知识、方法、思维经验，后续内容就应当在此基础上进行教学。但在教学中，我们常看到教师回归原点，忽视教材内容逻辑，忽视学生的知识、方法以及思维经验。备教材时，关注这种“瞻前顾后”的承接性十分必要。

（三）动态的视角析教材，有效设计教学活动

教学不应是“教教材”，而应是“用教材教”。这就需要教师以动态的视角解析教材。仍以案例中的分数乘分数为例，三个版本教材以过程全景图的形式呈现了计算的过程。教师备教材时可考虑以动态课件的形式呈现平均分的过程，选择表征方法的过程，再平均分的过程，以及确认结果分数的过程。此外，结合学生实际对教材情境恰当地进行再加工，对教学任务进行适当的分解、整合、重组等都是动态视角下解析教材的路径，也是有效设计教学活动的前提。

备教材是教师的基本功，教师要专精覃思读教材，读懂教材内容的本质与逻辑，为教学媒体和策略的选择提供依据，为实现高质量教学积蓄力量。

参考文献：

[1]WU H. Understanding numbers in elementary school mathematics[M]. Washington： American Mathematical Society， 2011： 263， 266， 267.

[2]卢江，杨刚.义务教育教科书数学六年级上册[M].北京：人民教育出版社，2019.

[3]刘坚，孔企平，张丹.义务教育教科书数学五年级下册[M].北京：北京师范大学出版社，2014.

[4]北京教育科学研究院.义务教育教科书数学六年级上册[M].北京：北京出版社，2014.

[5]JOHN A， WALLE V D， KAREN S. Elementary and middle school mathematics teaching developmentally：Tenth edition[M]. New York： Pearson Education， 2019： 392.

（北京教育学院   100120）