基于模糊C均值聚类的中药材鉴别研究
2022-06-30丁学利秦梦洁王静
丁学利 秦梦洁 王静

【摘 要】 以中药材的中红外光谱数据为聚类分析对象,通过提取影响药材类别的关键特征波数,采用主成分分析结合模糊C均值聚类建立了中药材的鉴别模型。该模型可实现对中药材样本数据的快速鉴别,为中药材鉴别问题的研究提供借鉴。
【关键词】 模糊C均值聚类;主成分分析;中药材鉴别
Identification of Traditional Chinese Medicine Based on
Fuzzy C-Means Clustering
Ding Xueli, Qin Mengjie, Wang Jing
(Fuyang Institute of Technology, Fuyang 236031, China)
【Abstract】 Taking the mid infrared spectrum data of traditional Chinese medicine as the cluster analysis object, the identification model of traditional Chinese medicine was established by extracting the key characteristic wave number affecting the category of traditional Chinese medicine and using principal component analysis combined with fuzzy C-means clustering. This model can not only realize the rapid identification of traditional Chinese medicine sample data, but also provide reference for the research of practical traditional Chinese medicine identification.
【Key words】 fuzzy C-means clustering; principal component analysis; identification of traditional Chinese medicine
〔中圖分类号〕 O212 〔文献标识码〕 A 〔文章编号〕 1674 - 3229(2022)02- 0013 - 06
0 引言
我国的中药材资源丰富,种类繁多,品种分布广泛。不同种类的中药材特征差异显著,但同一种药材不同产地的差异不太显著。目前对中药材进行鉴别分析一般采用近红外或中红外光谱分析方法[1-2]。基于红外光谱特征对中药材进行鉴别,一般要先对光谱数据进行降维处理,然后再聚类分析。光谱数据特征波数提取的方法有导数法、平滑法、傅里叶变换法、主成分分析法、偏最小二乘法等[2]。对中药材分类识别的方法一般使用K均值聚类法、层次聚类法、支持向量机和人工神经网络等[3-4]。本研究选取2021年高教社杯全国大学生数学建模竞赛[5]E题问题一的数据,解决关于425个中药材样本的鉴别问题。这是一个无监督的聚类问题,由于中药材样本之间的相似性非常高,且数据量大,若单纯使用聚类算法较难实现对样本数据的准确分类,因此本文运用主成分分析法结合模糊C均值聚类建立中药材的鉴别模型,为识别中药材提供快速有效的鉴别方法。
1 数据处理与分析
1.1 异常数据处理
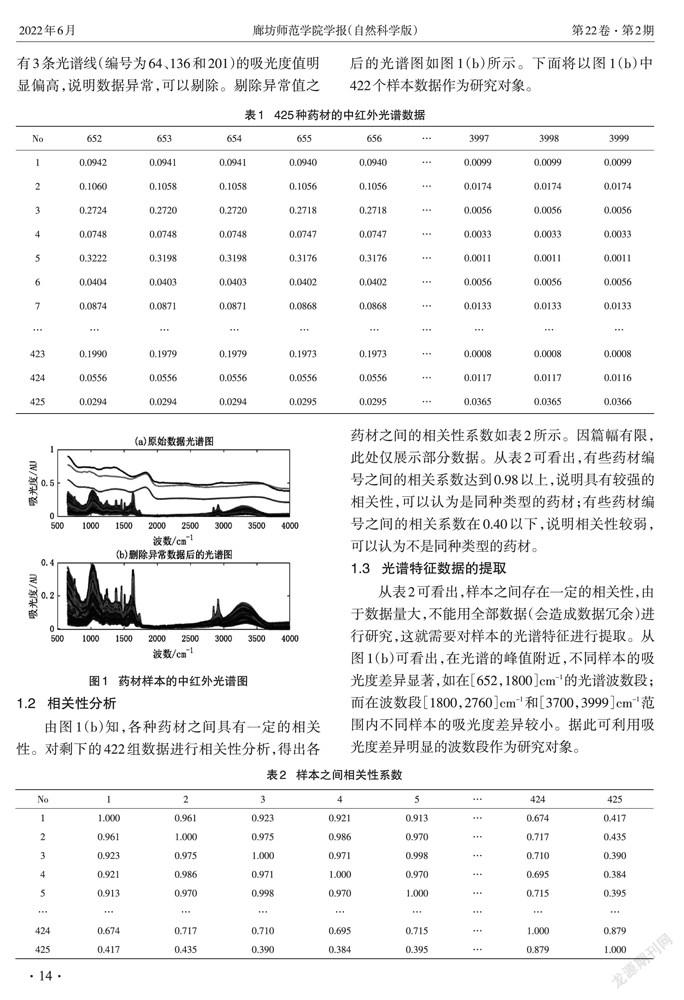
本研究使用的数据来源于2021年全国大学生数学建模竞赛E题的附件1,如表1所示。表1中No列为药材编号,其余各列第一行的数据为光谱的波数(单位cm-1),第二行以后的数据表示该行编号的药材在对应波段光谱照射下的吸光度(单位AU)。表1中一共有425个样本,3348个波段的中红外光谱数据,其光谱图如图1(a)所示。从图1(a)看出,有3条光谱线(编号为64、136和201)的吸光度值明显偏高,说明数据异常,可以剔除。剔除异常值之后的光谱图如图1(b)所示。下面将以图1(b)中422个样本数据作为研究对象。
1.2 相关性分析
由图1(b)知,各种药材之间具有一定的相关性。对剩下的422组数据进行相关性分析,得出各药材之间的相关性系数如表2所示。因篇幅有限,此处仅展示部分数据。从表2可看出,有些药材编号之间的相关系数达到0.98以上,说明具有较强的相关性,可以认为是同种类型的药材;有些药材编号之间的相关系数在0.40以下,说明相关性较弱,可以认为不是同种类型的药材。
1.3 光谱特征数据的提取
从表2可看出,样本之间存在一定的相关性,由于数据量大,不能用全部数据(会造成数据冗余)进行研究,这就需要对样本的光谱特征进行提取。从图1(b)可看出,在光谱的峰值附近,不同样本的吸光度差异显著,如在[652,1800]cm-1的光谱波数段;而在波数段[1800,2760]cm-1和[3700,3999]cm-1范围内不同样本的吸光度差异较小。据此可利用吸光度差异明显的波数段作为研究对象。5831760F-8CE3-4ADD-9B8A-586364E6592E
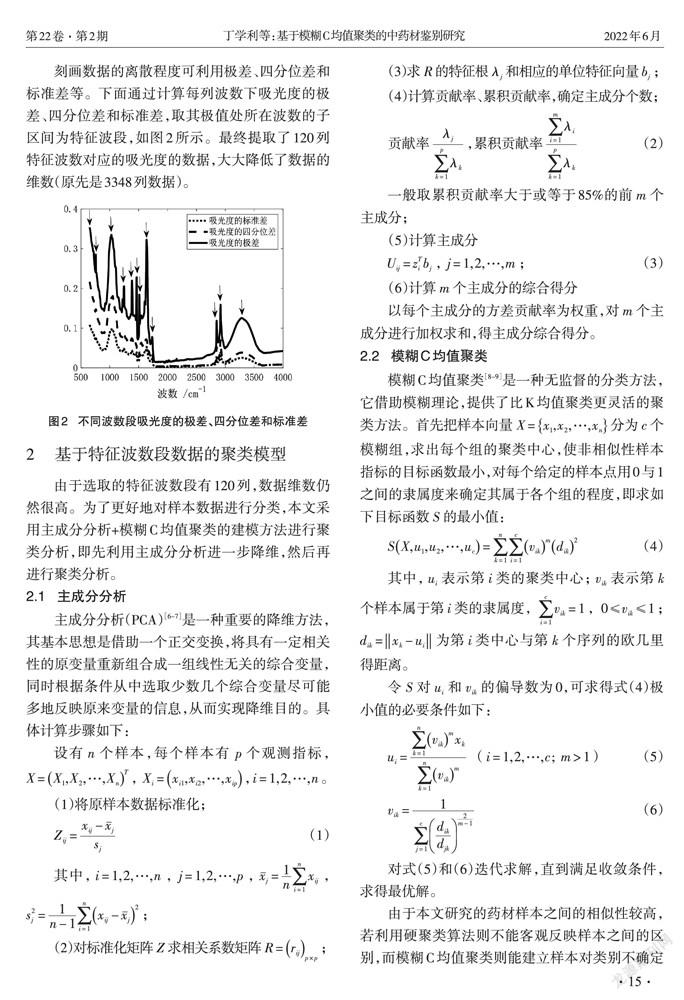
刻画数据的离散程度可利用极差、四分位差和标准差等。下面通过计算每列波数下吸光度的极差、四分位差和标准差,取其极值处所在波数的子区间为特征波段,如图2所示。最终提取了120列特征波数对应的吸光度的数据,大大降低了数据的维数(原先是3348列数据)。
2 基于特征波数段数据的聚类模型
由于选取的特征波数段有120列,数据维数仍然很高。为了更好地对样本数据进行分类,本文采用主成分分析+模糊C均值聚类的建模方法进行聚类分析,即先利用主成分分析进一步降维,然后再进行聚类分析。
2.1 主成分分析
主成分分析(PCA)[6-7]是一种重要的降维方法,其基本思想是借助一个正交变换,将具有一定相关性的原变量重新组合成一组线性无关的综合变量,同时根据条件从中选取少数几个综合变量尽可能多地反映原来变量的信息,从而实现降维目的。具体计算步骤如下:
2.2 模糊C均值聚类
3 结果分析
3.1 主成分分析结果
以选取的120列特征波數作为观测指标,进行主成分分析,得到解释的总方差如表3所示。表3中,第2和第3个主成分的累积贡献率分别为94.6293%和98.5520%。考虑到数据的复杂性,本文选取前3个主成分进行分析。
根据公式(3)可分别计算出每个主成分的得分,如表4所示。表4中,F1、F2、F3分别表示第一、第二和第三主成分得分。主成分的综合得分F可由F1、F2、F3与每个主成分的方差贡献率构成的线性组合计算得到:
F=78.7052%F1+15.9241%F2+3.9228%F3 (7)
图3是前2个主成分得分和前3个主成分得分图。根据图3结果,可考虑把422个样本数据分为3类或4类。
3.2 模糊C均值聚类结果
下面以主成分的综合得分F作为新的变量进行模糊C均值聚类。根据图3的提示,可考虑聚成3类或4类。为了更好地确定聚类数,计算不同类别对应的平均轮廓值和轮廓值分布图,如图4和图5所示。在图4中,类别数为2时,平均轮廓值最大,但分类太笼统。除类别数2之外,类别数为3时的平均轮廓值最大,说明类别数为3时较合适。另外从轮廓值的分布(图5)来看,分成2类、4类和5类时的轮廓值分布都出现负值,而分成3类时轮廓值分布都是正值。综合考虑图4和图5,可确定分成3类较合适。
设置分类数为3,利用模糊C均值聚类可得到图6所示的聚类结果。从图6可看出,聚类结果较为理想。第1类有193个样本,第2类有118个样本,第3类有111个样本,具体聚类结果,如表5所示。
为了更好地看出每类的聚类效果,绘制了如图7所示的3类光谱图。从图7可看出,第1类的主峰最大幅值在0.2 AU附近;第2类的主峰最大幅值在0.4 AU附近;第3类的主峰最大幅值在0.3 AU附近。每一类波形的幅值、峰的个数和形状等差异明显,说明每个样本都较好地进行了划分。
4 结语
中药材的鉴别是一个无监督的聚类问题,虽然这类建模问题的解决方法较多,但该问题数据量大,数据冗余性高,若单独使用聚类方法,较难给出合理的分类结果。本文首先根据光谱特征,利用极差、四分位差和标准差等实现对光谱特征数据的提取,其次应用主成分分析进一步降维,最后利用模糊C均值聚类给出合理的分类结果。该模型对中药材鉴别工作具有很好的理论指导和实际应用价值。
[参考文献]
[1] 汪方舟.近红外光谱建模法在中药质检中的应用[J].山东农业大学学报(自然科学版),2018,49(5):787-790.
[2] 周昭露,李杰,黄生权,等.近红外光谱技术在中药质量控制应用中的化学计量学建模:综述和展望[J].化工进展,2016,35(6):1627-1645.
[3] 周婷,付绍兵,谢慧敏,等.近红外光谱在川贝母及非川贝母品种鉴别中的应用[J].华西药学杂志,2021,36(2):193-197.
[4] 赵艳丽,张霁,袁天军. 近红外光谱快速鉴别不同产地药用植物重楼的方法研究[J].光谱学与光谱分析,2014,34(7):1831-1835.
[5] 2021高教社杯全国大学生数学建模竞赛赛题[EB/OL].http://www.mcm.edu.cn/html_cn/node/35bd4883c276afe39d
89.html,2021-10-01.
[6] 丁学利,曹文康,李玉叶.基于主成分回归的颜色与物质浓度辨识的研究[J].廊坊师范学院学报(自然科学版),2018,18(1):5-7+11.
[7] 彭文松.主成分聚类分析在广东省区域经济综合评价中的应用[J].廊坊师范学院学报(自然科学版),2013,13(1):61-65.
[8] 杨桂元.数学建模[M].上海:上海财经大学出版社,2015:112-117.
[9] 武艳,张莉莉,蒋志勋. 应用模糊C 均值聚类法判别同调机群正确性研究[J].廊坊师范学院学报(自然科学版),2011,11(4):43-45.5831760F-8CE3-4ADD-9B8A-586364E6592E
