基于监测状态和寿命随机效应辨识的剩余寿命预测*

危进波，钱新博，胡 鑫，李鹏飞

(武汉科技大学a.冶金装备及其控制教育部重点实验室；b.机械传动与制造工程湖北省重点实验室，武汉 430081)

0 引言

剩余寿命(remaining useful life,RUL)的预测是防止工业设备发生故障的重要过程之一，准确的RUL预测将有助于设备维护和健康管理，可以有效的防止大量的停机损失[1-2]，确保设备正常运行，改善安全问题，并降低生产成本，具有重要的理论和实际意义[3]。

近年来，剩余寿命的预测问题引起了广泛关注，LEI等[4]将剩余寿命预测方法分为3类，基于机理分析方法、基于数据驱动方法、以及联合分析方法。基于机理分析方法主要是在分析失效机理的基础上，通过构建物理模型来对设备进行剩余寿命预测[5-6]，但在实际应用过程中，大多数设备的物理模型难以构造，缺乏有效模型，历史经验依赖性强，使得该方法在一定条件下受到限制，基于数据驱动的方法是利用传感器收集到的退化数据，进行剩余寿命预测，具有数据挖掘和机器学习的特点[7]。联合分析方法指的是联合寿命数据和状态监测数据进行分析，相对于单独分析寿命数据和状态监测数据，该分析方法能够很好地将监测信息用于可靠性分析，并评估不同协变量对系统风险的影响，从而进行更准确的剩余寿命预测[8-9]。

在工程实际中，对于常见的复杂装备，比如航空引擎、数控机床等进行寿命预测是一项十分重要的课题，同时具有一定的挑战，由于在实际运行过程中通常会受到操作和环境条件的影响，如温度、海拔高度、湿度等，并伴随着大量高维数据的产生，仅利用退化数据或寿命数据进行寿命预测，其精度难以保证，因此结合现场的两类数据进行分析，有助于提高剩余寿命预测的准确度。联合分析方法主要包括两个子模型的构建，即两阶段模型法，基于监测数据构建协变量时变模型和基于寿命数据构建风险模型，第一阶段：通过时变模型拟合时变协变量，估计缺失或者真实的协变量值；第二阶段：将协变量估计值代入风险模型中，构建风险模型，进行风险分析。针对时变模型，王晓燕[10]对时变退化建模进行了系统的综述，包括利用维纳(Wiener)过程、马尔科夫链(Markov)对退化过程进行研究，此外，SI、袁捷等[11-12]基于线性混合效应模型对退化过程进行建模分析。针对风险模型，YU等[13]对常用的风险模型进行了系统的综述，包括比例风险模型(proportional hazard model，PHM)[14-15]、加速失效时间模型(accelerated failure time model,AFT)[16-17]等风险模型。由于加速失效时间模型对结果的解释更加简单、直观、易于理解，能够最大限度的利用数据，受到了广泛青睐[18-19]，对于两阶段模型法，HU等[20]将两阶段模型法应用于铅酸电池进行剩余寿命预测，YUE等[21]利用两阶段模型法对设备进行可靠性分析。

由于测量误差、运行工况和环境等因素的影响，导致样本间存在一定退化差异性[22-23]，而常规的两阶段联合分析法暂未考虑到样本之间的异质性，所以本文拟采用联合模型(joint model，JM)，以辨识出随机效应，并将其作为联合模型的基础同时进行参数辨识，更有效的使用数据，从而提高剩余寿命预测精度。JM模型是目前医学研究中比较热门的方法,主要应用于药物疗效以及患者寿命评估等方面[24-25]。但在可靠性工程领域中的研究和应用相对较少，还需进一步研究。

对此，本文提出了基于监测状态和寿命随机效应辨识的剩余寿命预测方法。通过线性混合效应模型进行退化建模，处理退化过程中样本间差异的随机效应，利用加速失效时间模型将寿命和监测状态结合。将随机效应作为两模型的基础，构建联合似然函数，进行参数辨识，提高模型的预测精度。利用蒙特卡罗模拟方法预测样本的可靠度，最终进行剩余寿命估计。

本文的其余部分组织如下。第1章介绍基于状态监测和寿命数据的联合模型，第2章为算例分析，第3章为结论与研究展望。

1 基于状态监测和寿命数据的联合模型

1.1 联合模型框架

本节主要介绍基于状态监测和寿命数据的联合模型框架，其联合模型剩余寿命预测流程图如图1所示。

该方法主要包括参数辨识和剩余寿命预测两大模块，参数辨识模块首先基于历史监测数据和寿命数据训练集样本构建联合模型，即状态监测和寿命的两类子模型构建，其中包含协变量筛选等主要步骤，其次通过定义联合模型的联合分布，构造联合似然函数，利用极大似然法进行参数辨识。而剩余寿命预测模块首先基于辨识出的参数和测试集样本构建可靠度函数，其次通过蒙特卡罗仿真算法完成参数更新，得到联合模型的可靠度预测函数，最终计算出剩余寿命。第1.2～1.4节分别对两类子模型的构建、基于随机效应的联合模型参数辨识，以及基于联合模型的剩余寿命预测进行了具体概述。

1.2 状态监测和寿命的两类子模型

(1)

为将监测数据真实值与事件结果联合，并考虑其他协变量对风险函数的影响，本文将采用加速失效时间模型[17-18]进行风险分析，模型基本形式如下：

(2)

式中，Mi(t)={mi(u),0≤u≤t}表示真实监测数据的历史序列；h0(·)表示基线风险函数；ωi为基线协变量(一般指非时变协变量，比如温度、压力等不随时间变化的参数，但对故障风险有影响)，其中mi(t)不同于yi(t)，后者表示在t时刻监测结果具有一定监测误差，γ为基线协变量的回归系数。参数α表示真实的监测结果对事件风险的影响。为了避免参数化假设产生偏差，在单独进行风险分析时，基线风险函数h0(·)一般未指定明确的分布形式。但在构建联合模型过程中，需要明确基线风险函数的分布形式，例如威布尔分布、对数正态分布等常见分布形式，或分段函数以及回归样条法等其它分布形式[26]。

1.3 基于随机效应的联合模型参数辨识

本节主要对模型参数进行辨识，将描述退化过程中样本间差异性的随机效应bi作为联合式(3)的基础，通过极大似然方法[27]来辨识参数，使得事件发生时间和监测结果的联合分布{Ti,φi,yi}的对数似然函数最大化，辨识出联合模型参数λ=(η,D,σ,γ,α)。同时意味着随机效应解释了监测状态和寿命之间的关联，也解释了在监测过程中重复监测之间的条件独立性，表达式如式(4)、式(5)所示。

(3)

p(Ti,φi,yi|bi;λ)=p(Ti,φi|bi;λ)p(yi|bi;λ)

(4)

(5)

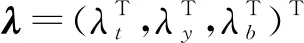
(6)

式中，生存部分的似然函数可以表示为：

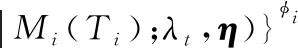
(7)

hi(·)由式(2)可得，Si(·)部分如下：

(8)

式中，p{yi(tij)|bi;λy}为监测值的单变量正态密度函数；p(bi;λb)为随机效应的多元正态密度函数。

1.4 基于联合模型的剩余寿命预测

在本节中，主要研究基于联合模型框架的剩余寿命预测，目前联合模型主要基于n个测试集样本拟合，并提供t时刻之前的历史监测数据yi(t)={yi(s),0≤s≤t}，意味着在时间t未发生故障。而剩余寿命预测关键步骤是求得条件可靠度，即未来u时刻的可靠度，如下：

(9)

式中，u>t；Dn表示拟合联合模型的样本，使用贝叶斯公式可以求解，式(9)可表示为：

(10)

被积函数第一部分通过式(4)可以表示为：

(11)

(12)

式中，L表示蒙特卡罗样本的数量，通过对可靠度进行积分求解，设备在时间t剩余寿命能表示为：

(13)

2 算例分析

2.1 原始数据

在本案例研究中，将基于飞机引擎的退化数据集[29]，评估所提出的联合模型预测性能，该数据集由航空推进系统模拟(C-MASS)生成，为一系列从开始运行到失效的数据，共 26 种参数，即1个引擎参数和运行次数、3个运行工况参数与 21 个由传感器记录的状态监测参数，如表1所示。其中历史数据为100个飞机引擎从开始运行至失效的信号数据。

表1 原始数据参数

由原始数据信息可知，总共有24种信号数据，即24种变量，为避免数据量纲带来干扰，利用数据归一化对其进行处理。为验证模型的有效性，本文通过留一交叉验证法将飞机引擎退化数据进行分类，选取其中99台设备作为联合模型的训练集，1台作为测试集，预测所有设备在不同预测起点的剩余寿命，设置测试集的预测起点间隔为40次，即预测起点tj=40、80、120，...，520次，其中最长飞行时间为525次，计算每次实例中RUL预测值的平均绝对误差(MAE)，并与常规的两阶段模型法[20]进行对比，MAE表达式如下：

式中，RULK(tj)和Tk(tj)分别表示k个测试样本在预测起点tj时刻的RUL预测值和真实值。

2.2 结果分析

通过R软件对监测变量进行风险函数显著性分析，选取最显著变量LPT冷却流量W32作为退化过程监测值yi(t)，将3种不随时间变化的运行工况，包括海拔高度、马赫数、海平面温度作为固定效应，同时将每个样本在监测时刻的异质性作为随机效应，并考虑监测误差，进行线性混合效应模型拟合。由于线性混合效应模型需要假设监测值服从正态分布，因此首先进行数据正态性检验，检验结果如图2所示。

图2 监测变量W32图形化正态性检验

从图2结果可知，在正态QQ图中近似接近一条直线，则数据服从正态分布，符合线性混合线性效应模型拟合变量的数据特征要求。在加速失效时间模型中，将基线风险函数h0(·)假设服从威布尔分布，并将运行工况以及变量W32真实值作为式(2)中ωi和mi(t)，利用R软件程序包实现整个联合过程，以及参数求解。为更好地说明，其中训练集为设备#1～#28、#30～#100的联合模型函数表达式如下：

式中，εi(t)～N(0,0.0732)；bi0～N(0，0.0782)；bi1～N(0，0.001 12)，为了验证模型的准确性，对联合模型结果进行分析，其诊断结果如图3所示。

图3为联合模型诊断结果，能划分为两种拟合结果。上面两个图表示线性混合效应模型拟合结果，下面两个图形表示加速失效时间模型拟合结果。左上角图为监测数据时间序列中样本的残差和拟合值的图，残差随机地分布在标准残差等于0的直线上，表明拟合效果比较好；右上角图描述了线性混合效应模型拟合过程中的正态QQ图，样本数据分布在一条直线上，表示该模型拟合效果较好；左下角图描述了风险过程的边际生存函数的估计曲线，右下角图描述了边际累积危险率函数的估计曲线，通过联合模型诊断图可得该模型的拟合效果较好。

图3 联合模型诊断图

为了更好地说明模型预测性能，本文将预测所有设备在不同预测起点下的剩余寿命，并与两阶段模型法[20]进行对比，其预测结果的MAE如图4所示，由图可知本文所提出的模型有较好的效果，预测结果的平均绝对误差整体小于两阶段模型法，随着可用数据增加，预测精度逐渐提高，特别在早期阶段，模型优势更明显。

图4 留一交叉验证RUL预测的MAE

为了更好地说明，图5显示了#3、#29、#71、#81设备的预测结果。由图可知，几乎在所有的预测时刻tj，预测的RUL区域大都包含了真实的RUL。

图5 不同设备在不同的预测时刻RUL的真实值和估计值

此外还给出了设备#29在tj=120和200更详细的预测结果。由式(12),预测的可靠度及其置信区间如图6所示。正如预期那样，随着更多数据的可用，预测精度提高，点分位间隔会变窄。

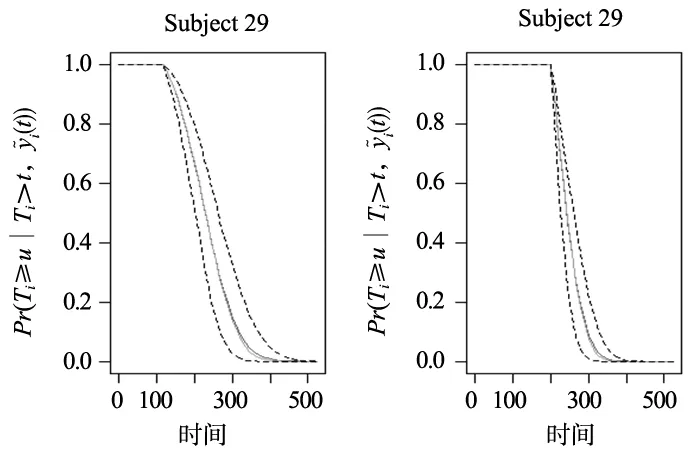
(a) tj=120 (b) tj=200

由式(13)可得设备#29在tj=120和200时剩余寿命分别为87和26，如表2所示，由于设备在飞行223次发生故障，可知随着更多监测数据可用，预测精度不断提高，预测结果较好，为了进行对比，还给出两阶段模型法的预测结果，它再次验证了本文模型的有效性。

表2 设备#29在tj=120和200时刻的RUL预测值

3 结论

针对不同样本在退化过程中产生的差异性，本文提出了基于监测状态和寿命随机效应辨识的RUL预测方法，该方法使用线性混合效应模型进行退化建模，处理了退化过程中样本间差异的随机效应，利用加速失效时间模型将监测状态和寿命进行联合，并将随机效应作为两模型的基础，同时对模型进行参数辨识，通过蒙特卡罗方法估计出设备的可靠度，并计算得到设备的剩余寿命。案例分析结果表明，本文提出的剩余寿命预测方法有较好的预测效果，与常规两阶段模型法相比，预测结果的平均绝对误差整体小于两阶段模型法，特别在早期阶段，模型优势更明显。

本研究仅考虑了单一时变协变量对风险函数的影响，进行联合建模分析，而随着操作和环境条件的变化，可能还会存在多种时变协变量的混合形式来影响风险函数，从而影响剩余寿命预测的精度，此外本文仅基于飞机引擎退化数据进行案例分析，该研究方法在数控机床等其他领域的应用有待进一步展开。