航空薄壁件压铆质量控制研究*
2022-06-29王明阳王建新
郝 博,王明阳,王建新
(东北大学航空动力装备振动及控制教育部重点实验室,沈阳 110819)
0 引言
薄壁零件因具有质量轻、承载效率高等优点被广泛应用于飞机等装备制造中[1]。壁板、蒙皮等薄壁件作为飞机外形的关键组件,其压铆质量对于保障气动特性、连接强度有着较大的影响,而压铆后镦头的尺寸则是其重要影响因素之一[2]。
压铆质量控制是通过实时分析当前的压铆质量数据,并将分析结果反馈回生产车间,生产车间据此进行相应调整和管制,最终使压铆质量数据保持在合理范围内[3]。关于压铆质量控制的问题,国内外学者进行了相关研究。ZENG等[4]基于弹塑性变形理论建立了压铆过程的解析模型。LEI等[5]通过理论分析、数值分析和实验验证,揭示了铆钉模具结构与压铆质量之间的内在联系。ZHANG[6]探究压铆顺序和方向对压铆变形的影响。RIJCK等[7]基于压缩变形理论和幂指数硬化理论,构建了压铆过程中压铆力和镦头高度、直径尺寸的物理模型。YIN等[8]建立了铆钉直径-钉孔直径-最大压铆力之间的数学模型。符文科等[9]通过数值模拟研究了钉杆外伸量与干涉量之间的关系。常正平等[10]采用局部-整体映射模型的壁板压铆变形预测方法,并构建了变形预测模型。NOLLER等[11]利用机器学习监测故障铆接点。魏文杰等[12]研究不同搭接顺序下自冲铆接头的损伤特性。
综上所述,目前关于压铆力、镦头尺寸建模的研究并不多,考虑镦头端面摩擦力影响并建模的研究更是较少报道。另外,传统的研究无法将分析结果及时反馈给生产车间,很容易造成误差累积。
数字孪生技术不仅可以实现物理车间和虚拟车间交互融合与迭代,更重要的是虚拟车间可以根据物理车间的生产状态信息作出分析和决策并反过来指导物理车间进行相应的调整和管控[13]。
针对航空薄壁件压铆质量监控滞后、误差累计等问题,提出航空薄壁件压铆质量控制模式,在实现压铆力数据实时采集的基础上,虚拟车间利用压铆力-压铆质量模型、质量离差算法实现压铆质量实时监测及判断,并以此为据向物理车间发送预警命令,工人根据预警进行相应的调整和补救,最终实现薄壁件压铆质量实时、动态管控。
1 压铆质量控制总体流程
传统航空薄壁件压铆质量控制时,依赖质检人员抽样检测,准确性差、效率低且质检人员无法实时监控物理车间的压铆质量状态,往往是整个零件甚至部件装配完成后才进行抽样质量检测,容易出现装配误差累计,影响生产质量及效率。而压铆质量数据作为压铆质量控制的重要信息源通常被埋没在物理车间中,这使得企业在进行压铆质量管控时无据可依、可靠性差。综上,传统的压铆质量管控模式难以满足当前航空薄壁零件的质量要求。
本文将数字孪生技术应用到压铆质量控制中。首先,给物理车间配备过程监控铆枪并提取物理车间的关键装配过程要素,构建和映射虚拟车间;然后,工人手持过程监控铆枪进行日常压铆作业,数据服务平台实时采集压铆过程中的压铆质量数据,并经过异常值去除处理后进行整合存储,构成压铆孪生数据;最后,虚拟车间从压铆孪生数据库中调用压铆质量数据,利用压铆力-压铆质量模型、质量离差算法根据压铆质量数据规范进行偏离程度评估,并将结果反馈到物理车间,若当前压铆点的压铆质量数据满足质量要求,则物理车间继续进行压铆作业,反之,虚拟车间会及时对物理车间发送预警。航空薄壁件压铆质量控制技术架构如图1所示。

图1 航空薄壁件压铆质量控制技术架构
2 压铆力-压铆质量理论建模
2.1 压铆过程条件假设
为了研究和建模方便,本文忽略次要因素对压铆受力、变形的影响,做以下假设:①一般塑性条件假设(连续性假设、均匀性假设、各向同性、初应力为零、体积不变);②铆钉压铆前后,体积无变化;③钉杆圆柱度为零,即为标准圆柱体,钉杆与锥头端面垂直度为零;④顶铁与冲头均为理想刚体,压铆过程不发生变形。
2.2 压铆力-压铆质量理论模型
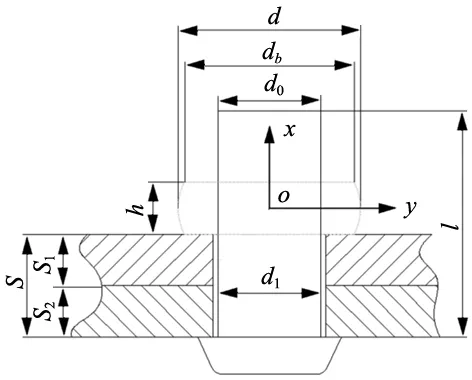
根据上述条件假设,钉杆形成镦头过程可视为圆柱体沿轴线镦粗,变形过程呈轴对称特点。在镦粗成型阶段,压铆力F逐渐增大直至到达最大值,作用在镦头上的正应力σz也随之增大,而镦头与冲头接触表面摩擦切应力τf的大小及分布情况也直接影响到正应力σz的分布规律。依据航空工业对镦头成型的质量要求[14],结合翁克索夫关于摩擦切应力的研究可知,压铆过程中,镦头与冲头接触表面上的摩擦力区域包括停滞区和制动区,根据翁克索夫实验研究可知,圆柱体端面摩擦停滞区范围为0≤r≤h,摩擦制动区范围为h 图2 铆钉镦粗变形及基元受力分析图 平锥头铆钉压铆过程可视为轴对称镦粗,因此,有平衡方程式: (1) σθhdr-2τfrdr-σrhdr-rhdσr=0 (2) 式中,σθ为周向正应力;σr为径向正应力;τr为冲头与钉杆接触面摩擦切应力;r为镦头半径;dr为镦头半径的微分;dσr为径向正应力的积分。 由于已假设钉杆为均匀镦粗变形,所以其径向正应力和周向正应力相等,即σr=σθ,从而式(2)可简化为: (3) 如前所述,此处仍按绝对值列简化屈服方程,因σr=σθ,所以有: σz-σr=Y (4) dσz=dσr (5) 式中,σz为钉杆受到的轴向正应力。 联立式(3)、式(5)可得: (6) 在摩擦制动区h (7) 对式(7)两侧不定积分可得: (8) (9) 在摩擦制动区的区域范围内对式(9)积分可得: (10) (11) 对式(11)两侧不定积分可得: (12) (13) 在摩擦停滞区的区域范围内对式(13)积分可得: (14) 因此,冲头对镦头的压铆力为: (15) 式中,σs为铆钉试件的屈服强度;h为镦头高度;μ为冲头与钉杆端面间的摩擦系数;rb为镦头端面的直径。 如图3所示,采用VMS-4030G型影像测量仪在镦头轮廓上取20个点,将以上点作为镦头轮廓曲线上的坐标点并据此拟合镦头轮廓曲线,可见镦头轮廓曲线符合二次函数,因此,记镦头轮廓曲线表达式为: (a) 镦头轮廓影像图 (b) 镦头轮廓坐标点及轮廓曲线 y=ax2+bx+c (16) 式中,a、b、c分别为二次项系数、一次项系数及常数项。 以镦头中心为原点建立直角坐标系如图4所示。 图4 镦头轮廓曲线解析计算坐标系 (17) 压铆结束后,镦头的体积为: (18) 由于对于确定装配点位的压铆连接,式(18)中的参数d0、l、d1、s均为已知,所以等号右侧可记为常数C。联立式(17)、式(18)可得: (19) 式(19)中db与d、h有关,满足关系式: (20) 联立式(19)、式(20)可得db、h、d相互之间的关系,从而,当限定d的尺寸时,可得到相应db、h的大小,代入式(15)可得最优压铆力。 压铆连接时,当镦头的尺寸在规定范围内时,铆接处连接强度最大,否则,铆缝的质量将变差,强度降低[14]。国标规定的镦头尺寸要求如表1所示。 表1 铆钉压铆后尺寸规定 (mm) 由表1可知,若想使压铆连接强度达到最优,则应限制压铆后镦头的尺寸。但是,压铆后镦头的尺寸无法直接进行控制,由式(15)可见,可以通过控制压铆力的大小进而控制镦头的尺寸。本研究以平锥头铆钉对蒙皮测试板、长桁测试板压铆进行测试。其中,平锥头铆钉型号为HB6298,尺寸为φ4×9 mm,材料为2A10,屈服强度为256 MPa,被连接件中蒙皮测试板、长桁测试板与机翼上的蒙皮、长桁的材质一样,分别为2A12、7075,尺寸为200×100×2 mm,冲头与镦头端面的摩擦系数为0.2[16]。 针对φ4×9 mm的平锥头铆钉,按照装配工艺要求,其铆接孔直径一般为4.1 mm,以上数据代入式(18)可得其压铆完成后形成镦头的体积为C=60.26 mm3,镦头直径应该限制在1.5±0.1d0,显然,当压铆力越大时,钉杆材料向径向扩展的越多,镦头的直径越大。取规定的镦头直径下限1.4d0,即5.6 mm,代入式(19)和式(20)可得:rb=2.64 mm,h=2.54 mm。将rb、h代入式(15)可得此镦头尺寸所需的压铆力为15 520 N。 取规定的镦头直径上限1.6d0,即6.4 mm,代入式(19)和式(20)可得:rb=2.98 mm,h=1.97 mm,将rb、h代入式(15)可得此镦头尺寸所需的压铆力为21 220 N。 综上可知,若压铆完成后镦头尺寸在规定范围内,即获得较好的压铆连接强度,则压铆力应该控制在15 520 N~21 220 N。 薄壁零件压铆变形属于复杂的非线性过程,因此,借助ABAQUS对其进行建模和有限元仿真,从而分析压铆力作用下铆钉材料的塑性流动以及镦头成型,并验证压铆力-压铆质量模型的有效性。 (1)几何模型 单个铆钉压铆仿真模型包括平锥头铆钉、测试板、冲头和顶把四个部分,其中平锥头铆钉、测试板的几何参数与理论计算时保持一致,而冲头和顶把的尺寸均为φ12×5 mm。 (2)材料属性 平锥头铆钉的材质为2A10铝合金,上、下层测试板的材质分别为2A12和7075铝合金,其材料性能参数如表2所示。由于压铆力属于冲击载荷,因此,将材料本构关系设置为J-C本构关系模型。由于冲头和顶把的刚度比铝合金大的多,因此,将其设置为刚体,仅与钉杆端面存在摩擦。 表2 铆钉与测试板材料性能 (3)网格划分 网格采用CAX4R单元,由于压铆过程的变形主要集中在钉杆区域,因此,铆钉采用加密网格,上、下测试板采用正常密度网格,而冲头和顶把几乎不发生变形,因此,采用较粗的网格,其中铆钉的网格单元数量为189 184个,上、下测试板的网格单元数量分别为327 340个、304 284个,冲头和顶把的网格单元数量分别为672个和804个。仿真模型网格划分结果如图5所示。 图5 压铆模型网格划分示意图 (4)边界条件及接触设置 约束平锥头铆钉沿X、Z方向的移动自由度以及沿X、Z方向的旋转自由度,约束顶把沿Y方向的移动自由度以及沿X、Z方向的旋转自由度,约束测试板沿Y方向的移动自由度以及沿X、Z方向的旋转自由度,冲头与铆钉同轴线,约束冲头沿X、Z方向的移动自由度以及沿X、Y、Z方向的旋转自由度,仅沿Y向加载压铆力。接触关系采用surface-to-surface contact,为获得较高的计算精度,各面间的接触采用有限滑移,以大刚度零件的平面为主面来设置主从面,摩擦系数与理论计算时相同,取0.2。 (5)载荷 将理论计算得到的15 520 N和21 220 N压铆力通过冲头作用于钉杆上,具有作用时间短、高速的特点,因此采用Explicit分析模块进行分析求解。 (6)模拟结果 压铆力作用后,钉杆发生塑性变形并形成镦头。平锥头铆钉压铆前后的Mises应力云图如图6所示。 (a) 压铆前的Mises应力云图 (b) 15 520 N压铆后的Mises应力云图 压铆完成后,为了观测镦头的直径和高度尺寸,将“Solution”通过“Export”指令导出“STL File”文件,然后用SolidWorks打开后测量上述尺寸信息,15 520 N压铆力压铆后,镦头半径、高度分别为2.91 mm、2.42 mm,与镦头理论计算值的相对误差分别为3.93%、4.72%;21 220 N压铆力压铆后,镦头半径、高度分别为3.31 mm、1.88 mm,与镦头理论计算值的相对误差分别为3.44%、4.57%。 镦头尺寸在日常飞机制造中被视为衡量压铆质量的重要指标和判定依据。为了验证本压铆力-压铆质量理论模型的准确度。采用YM-5S系列伺服压铆机对上述蒙皮测试板、长桁测试板进行压铆实验。利用伺服压铆机的控压功能,施加15 520 N和21 220 N的压铆力作用于φ4×9 mm的平锥头铆钉上,使蒙皮测试板、长桁测试板实现铆接,然后得出不同压铆力作用下对应的镦头尺寸,并与理论值比较来判定该模型的有效性。如图7所示,压铆完成后,用VMS-4030G型影像测量仪和LGK-0510型线性测微仪测量分别测量镦头的直径和高度。 (a) 影像测量仪测量镦头半径 (b) 影像测量系统软件界面 (c) 线性测微仪测量镦头高度 用15 520 N、21 220 N压铆力分别对φ4×9 mm的平锥头铆钉进行试验测试后,其镦头尺寸理论值、实测值及两者之间的相对误差如图8所示,其中,左侧纵坐标轴反映镦头尺寸,右侧纵坐标轴反映相对误差。 (a) 15 520 N压铆力作用下镦头半径 (b) 15 520 N压铆力作用下镦头高度 由图8可知,伺服压铆机用15 520 N压铆力作用于φ4×9 mm的平锥头铆钉后,镦头半径理论值与镦头半径实验值的相对误差取绝对值来同向分析相对误差偏离的程度,其最大值为4.44%、平均值为2.38%;镦头高度理论值与镦头高度实验值的相对误差最大为4.96%,平均值为2.92%;伺服压铆机用21 220 N压铆力作用于φ4×9 mm的平锥头铆钉后,镦头半径理论值与镦头半径实验值的相对误差最大值为4.58%、平均值为2.12%;镦头高度理论值与镦头高度实验值的相对误差最大为4.90%,平均值为2.94%。综上所述,镦头尺寸理论值与实验值相比,相对误差平均值均在5%以内,可以满足实际生产要求[14],从而认定该压铆力-压铆质量理论模型有效。因此,该模型根据被连接件材质、壁厚、润滑状况、铆钉尺寸等先知条件计算出的最优压铆力区间可用于指导实际生产。在日常生产中,通过监控压铆力的大小,进而监控压铆后镦头的尺寸。 绝对质量离差是指观测值与特定参考值间的差值,相对质量离差是指该差值与特定参考值的比值,用于反映质量偏离程度。基于质量离差的基本思想,将质量离差算法应用于压铆质量控制中,可以准确、高效的实现薄壁零件压铆质量实时监控,此时,实测质量数据是指实测的压铆力数据,特定参考值是指最优压铆力区间平均值。基于数字孪生的薄壁件压铆质量实时监测流程如图9所示。其中,用绝对质量离差算法计算实测压铆力数据与最优压铆力区间平均值的差值,并将该差值与最优压铆力区间长度的一半进行比较,若该差值比最优压铆力区间长度的一半还大,说明该实测压铆力数据不在最优压铆力区间内,无法满足压铆质量要求,反之,虚拟车间则默认当前压铆质量合格,无需调整。 图9 基于数字孪生的薄壁件压铆质量实时监测 为了进一步说明基于数字孪生的压铆质量控制模式在压铆生产中的具体实施效果,选用某型号机翼的蒙皮和长桁压铆连接为例进行实例分析,其中,蒙皮的材质为2A12,长桁的材质为7075,平锥头铆钉型号为HB6298,尺寸为φ4×9 mm,材料为2A10,屈服强度为256 MPa,蒙皮与长桁结构示意图如图10所示。 图10 蒙皮与长桁结构示意图 根据上述分析结果可知,若想获得较好的压铆连接强度,压铆力应该控制在15 520 N~21 220 N,记为(a,b),此时最优压铆力区间平均值为18 370 N,最优压铆力区间长度的一半为2850 N。如图11所示,工人在使用过程监控铆枪进行压铆作业时,过程监控铆枪可以实时采集压铆操作过程中产生的压铆力数据,其中,取15组蒙皮和长桁压铆时的压铆力数据,将其按照采集的先后顺序编号,即采集序号1~15。 (a) 过程监控铆枪 如表3所示,由式(21)~式(23)计算绝对质量离差、相对质量离差。绝对离差公式、相对离差公式如下: 表3 实测压铆力数据的绝对、相对质量离差 Δ=f(xi,x0)=|xi-x0| (21) {Δm∈Δ|Δm>(a+b)/2} (22) (23) 式中,xi为实测的压铆力数据;x0为最优压铆力区间平均值;Δ表示绝对质量离差;δ表示相对质量离差;Δm表示大于最优压铆力区间长度一半的绝对质量离差;a和b分别表示最优压铆力区间上下限。 由表2可知,采集序号为6、15的压铆点的绝对质量离差大于2850 N,则说明该压铆点处的实测压铆力数据不在最优压铆力区间内,此时,虚拟车间向物理车间发送停装调整预警,工人依据预警信息对相应连接处进行二次压铆。相对质量离差用于反映质量偏离的程度和衡量工人压铆操作的规范程度,其中,采集序号为6的压铆点的绝对质量离差为4 911.56 N,相对质量离差高达26.74%,说明该压铆点在进行铆接操作过程中压铆力严重偏离压铆质量要求,工人以此为依据注意下一阶段操作规范。通过物理车间和虚拟车间实时融合、交互,可以实现问题压铆点及时发现、及时补救,有效避免了压铆质量监控滞后及装配误差累计等问题,从而提高了薄壁零件的压铆质量和效率。 (1)基于工程计算法建立压铆力-压铆质量理论模型,并通过数值模拟和压铆实验验证了该理论模型的有效性,其中15 520 N、21 220 N压铆力作用下镦头尺寸平均相对误差均小于5%; (2)通过实例分析,验证了通过压铆力去间接控制镦头尺寸的可行性; (3)基于实测压铆力数据利用质量离差算法进行计算可以准确、高效的判断当前压铆质量是否满足压铆质量要求; (4)验证了航空薄壁件压铆质量控制模式的可行性,通过“感知—分析—决策—执行”四个环节实现压铆质量闭环控制。

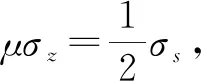



3 理论计算、数值模拟及实验验证
3.1 理论计算

3.2 数值模拟



3.3 实验验证


4 压铆质量控制模式
4.1 压铆质量实时监测

4.2 压铆质量控制实例分析



5 结论
