高中物理模型建构能力的测评及其培养——以2021年江苏、河北、广东、湖南高考试题为例

杨 科 张文悦 张 静

（长江大学物理与光电工程学院物理教育研究所，湖北荆州 434023）

模型作为真实事物的表征，是学生认识世界的手段和工具；建模作为科学学习中重要的一种能力，成为科学教育研究领域的热点并获得多国科学课程标准的重视.［1，2］物理学在培养学生科学建模能力方面具有重要的作用.模型建构作为物理学科核心素养中科学思维的关键要素，［3］能够充分培养学生的分析、综合、抽象、概括等思维方法.

2021年，江苏、河北、广东、湖南等8省市进行第3批新高考改革，［4］新高考命题注重对模型建构等物理学科核心素养要素的考核，凸显了其命题理念中核心素养的导向作用.本文以2021年江苏、河北、广东、湖南4 省份新高考物理中涉及模型的试题为研究对象，采用内容分析法，从质性和量化两个方面对新高考试题中所考查模型类型和模型建构能力水平进行分析，以期从测评的视角为教师有针对性的培养学生模型建构能力提供参考.

1 模型分类及能力水平划分

2017版物理课程标准中多次提到“模型”一词，要求学生具有建构模型的意识和能力.科学教育领域中，许多学者从多角度对模型进行分类.［5，6］目前，大多数学者较认可物质模型与过程模型，在此基础上参考其他学者的分类标准，将模型确定为物质模型、过程模型、状态模型和模拟模型4大类，其内容见表1.

表1 模型分类

课程标准将模型建构能力划分为5个水平层级，参考模型建构的相关研究成果，［7，8］对课程标准划分的模型建构能力水平的内涵进行补充（见表2）.其中水平1属于模型的再认与回忆；水平2要求在熟悉的物理情境中对模型的简单应用；水平3要求能结合模型的条件与有关物理规律进行模型选择；水平4 注重在实际问题中建构物质模型与过程模型，且需将物理模型与相关物理规律结合；水平5中的实际问题情境比水平4复杂，需建构多个过程模型.

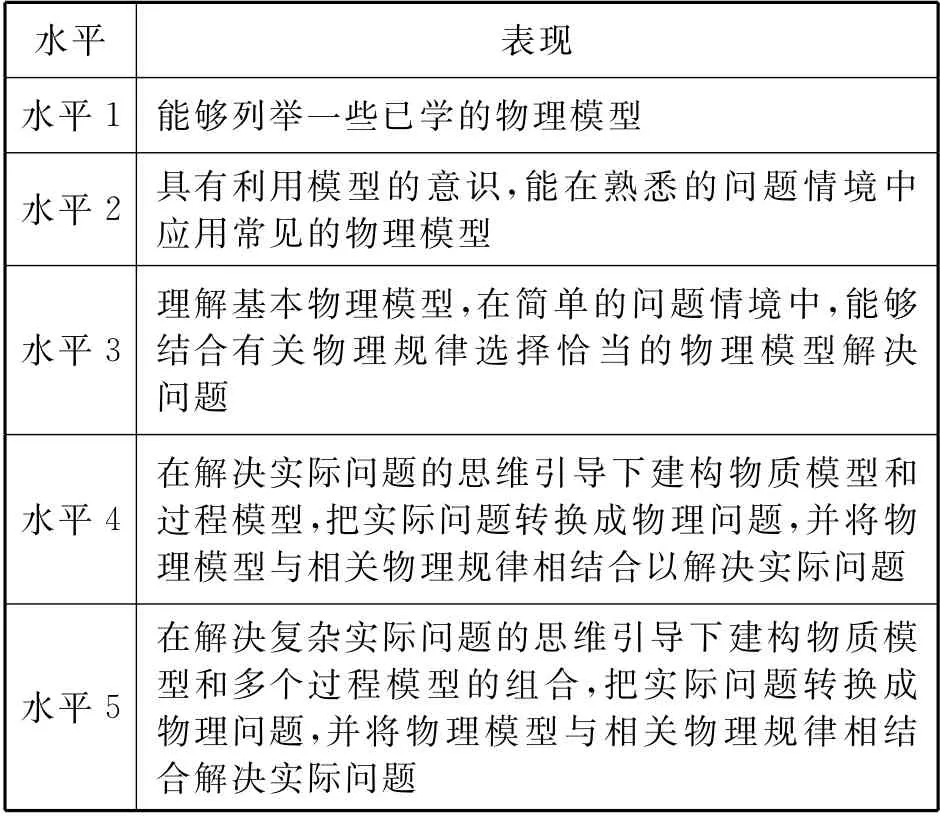
表2 模型建构能力的5级水平

2 模型建构能力考查情况

为保证内容分析的可靠性和一致性，两名具有教育背景的研究者独立对新高考试题的模型类别和能力水平展开分析，两位研究者的一致性系数为0.845，表明研究结果具有良好的内部一致性，通过协商，最终达到一致.统计结果显示，4省份新高考物理试题中江苏卷的试题总数为15，另外3省份试题总数均为18（每个选考模块记2题），其中涉及模型的试题数分别为14、16、16、17，其占比分别为93%、89%、89%、94%.

2.1 4类物理模型的考查

根据模型分类标准，对4 省份新高考物理试题中的模型类型进行统计（见图1）.结果表明，新高考物理试题对4 类模型展开不同程度的测评，其中物质模型在4 省份高考试题中的占比最多，其次为过程模型，而状态模型与模拟模型的总占比仅为11%，其占比远小于物质模型和过程模型.

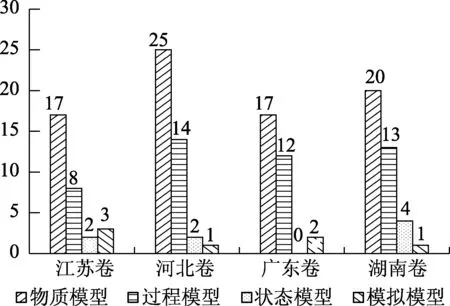
图1 4类模型考查情况

对所考查的物质模型进行分析表明（见图2），质点模型在物质模型中的占比最高，达到29%，匀强磁场、点电荷两种模型其次，均达到13%，而光波、机械波、光电子模型仅在4套高考试题中总共出现了1次.可见高考更多考查诸如质点、点电荷等与多数物理概念有所联系的模型，也不乏对光波等模型的考核.

图2 物质模型考查情况

过程模型中的匀变速直线运动、圆周运动（包括匀速圆周运动）的频次较多，考查频次占比均为26%，这两种模型在力学、电磁学等考题中均有所涉及.

2.2 模型水平的考查

基于模型建构的5 个能力水平，对物理试题的水平进行统计，各模型建构水平的百分比见图3.模型建构能力水平的测验集中于水平2、水平3和水平4，其中水平3的数量最多，且广东卷中水平3要远高于其他水平；而水平5 的考查总频次为5，水平1则完全未涉及.虽然学业质量水平4是高考的命题依据，但多省份的模型建构水平集中在水平3，即能够结合模型的条件与有关物理规律进行模型选择，其次为水平4和水平2（仅广东卷的水平2高于水平4）.

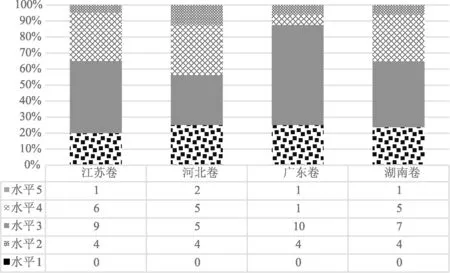
图3 4省份模型建构水平的考查情况

3 试题情境分析

情境作为高考评价模式的考查载体，［9］4省份通过设置多类型的情境化试题，从不同水平考查学生的模型建构能力.统计结果表明，新高考试题涉及的情境主要有4 个方面：生产生活方面的情境，如“复兴号”动车组、曲杆道闸、玻璃保温杯等；体育竞技方面的情境，例如篮球投篮、滑雪等；中华优秀传统文化方面的情境，例如曲辕犁和直辕犁、算盘、赛龙舟等；现代科技成果方面的情境，如“天问一号”探测器、“天和”核心舱、“北斗”卫星、薄膜材料制备技术等.

3.1 相同情境试题分析

太空探索新技术作为高考试题的问题情境，“天问一号”是我国首次火星探测任务的探测器，为我国行星探测的第一步，“天和”核心舱成功发射标志着我国空间站在轨组装建造全面展开.河北、广东、湖南3省份均以我国太空探索新技术为问题情境（见表3），通过设置不同层次的问题来考查学生的模型建构能力.基于此问题情境，学生需建构两个物理模型：质点模型和匀速圆周运动模型，再结合万有引力定律、牛顿第二定律、向心力等内容来解决问题.

表3 相同情境类试题

但3道试题所考查的具体知识及模型建构水平有所差别：广东卷涉及的知识为中心天体质量求解，虽然该问题情境对学生而言较陌生，但题目中已建构匀速圆周运动模型，学生需将匀速圆周运动模型与万有引力定律、牛顿第二定律等物理规律相结合，便可得出结论：已知的物理量为①核心舱的绕地线速度和绕地半径；②绕地角速度和绕地半径；③绕地周期和绕地半径均可求得地球的质量，故其属于模型建构的水平3；湖南卷则对圆周运动的相关物理量进行比较，该试题为一个实际问题，学生需根据核心舱绕地球运动时其大小和形状可忽略建构质点模型（物质模型），根据运动轨迹为圆轨道建立匀速圆周运动模型（过程模型），把实际问题转换为物理问题，并将匀速圆周运动模型与万有引力定律、牛顿第二定律等物理规律结合运用便可求得结果，其属于水平4；河北卷就火星与地球的轨道半径进行比较，该试题也为实际问题，学生同样需要根据试题内容建立质点和匀速圆周运动模型，且将匀速圆周运动模型与万有引力定律、牛顿第二定律等相结合，其属于水平4.基于同一类问题情境，三套试卷所考查的具体知识与模型建构水平有所差别，但其模型建构的过程相似.

3.2 不同情境试题分析

共点力的平衡是高中物理“运动与相互作用关系”的起始内容，对运动与相互作用观的形成具有重要的作用，该内容的运用需要结合平衡态模型.江苏卷的第13 题与湖南卷第15题均需建立平衡态模型，其问题情境有所区别（见表4）.

表4 不同情境类试题

面对上述两道试题的情境，学生需先依据物体静止或匀速的运动状态建立平衡态模型，再结合共点力的平衡条件来确定物体所受到的力，进而转换为热力学问题.两个试题均需将平衡态模型与共点力的平衡条件相结合，江苏卷第13 题需根据题目中的“缓慢”字眼建立平衡态模型，结合受力平衡的条件得出气体压强，其次通过热力学第一定律求得内能的增加量，故属于水平3；湖南卷第15 题需依据杠杆的平衡建立平衡态模型，同时根据系统的体积不变建构等容变化模型，并需结合受力平衡的条件得出系统的压强，利用查理定律求得温度，故属于水平4.可见，对同一模型建构和相同知识理解的考查，新高考试题巧妙设置多种问题情境来测试学生的模型建构能力.

4 总结与建议

新高考物理十分重视对物理模型与模型建构能力的考查；重点对物质模型与过程模型进行测评；侧重模型建构水平3的考查，也注重通过多种模型的组合来检验学生的模型建构能力；问题情境设置呈多样化的特点.

（1）重视建模教学，提升学生高阶思维.

科学研究是模型的建构过程，科学学习则是学习模型建构的过程.［10］教师可利用建模教学模式引导学生经历选择、建立、验证与重构等模型建构的过程，体会在建构物理模型过程中运用的抽象、概括等思维方法，发展学生的模型建构能力并培养学生分析、综合等高阶思维.

（2）融入真实情境，增强学生建模能力.

学业质量水平与问题情境的复杂程度、开放性程度等有关，学业质量水平对问题情境的描述体现了由简单到复杂、由物理问题到实际问题的复杂度进阶.近年来，生产生活、当代体育竞技、优秀传统文化及现代科技前沿等真实问题成为高考的热点情境，如2021年新高考中设置了玻璃保温杯、太空探索新技术、曲辕犁和直辕犁等多样化的真实情境类试题，学生利用抽象、概括等物理思维方法来建构相应的物理模型，将真实情境转换为非情境化的物理问题是解决问题的关键.教师可适当融入真实问题情境于课程教学、课后作业与阶段性评价中，充分利用真实问题情境发展学生的模型建构能力.

（3）多维整合，发展学生核心素养.

物理观念的形成过程是发展学生模型建构的重要途径，模型与建模在物理观念的形成中起着基础性的作用，［11］物理学科核心素养各要素是相辅相成、协同发展的.新高考试题中注重将核心素养的多个要素进行整合测试，如江苏卷第13题将运动与相互作用观与模型建构相结合，太空探索新技术将我国对科学的探索精神渗透在物理观念和科学思维的考查之中.