带有转动摩擦阻尼器钢框架的抗震性能分析
2022-06-29张海宾
吕 婷,王 燕,*,张海宾
(1.青岛理工大学 土木工程学院,青岛 266525;2.山东莱钢绿建发展有限公司,青岛 266101)
我国地震活动表现为震源浅、分布广、频度高、强度大,唐山、汶川等大地震对我国传统建筑房屋造成巨大破坏。提高建筑结构抗震能力,减小大地震灾害是结构研究领域永恒的主题。建筑结构传统抗震设计方法一般通过增加结构抗侧刚度或利用结构或构件的变形消耗地震能量。但在强震作用下结构或构件过大的变形将导致结构产生不同程度破坏,甚至倒塌。耗能减震技术[1]是通过设置在结构特定位置耗能装置的滞回变形耗散地震能量,达到减震设计目标。摩擦阻尼器作为一种减震装置,因其耗能能力强、构造简单、价格低廉,被广泛应用于中高层结构中。转动摩擦阻尼器是由希腊学者MUALLA[2]最早提出的,构造如图1所示。
摩擦耗能装置与框架支撑协同工作组成摩擦耗能支撑框架(Friction Damped Braced Frame,简称FDBF)。图2所示为L形转动摩擦阻尼器在钢框架结构中的应用。在小震作用下,摩擦耗能支撑不产生滑动,主体结构处于弹性状态,摩擦耗能支撑相当于普通支撑,仅为结构提供侧向刚度;在中震或大震作用下,摩擦耗能支撑在主体构件屈服之前,按预定滑动荷载产生滑移,提供依靠摩擦耗散能量的机制。摩擦耗能支撑在滑移过程中不仅可以消耗大量的地震能量,还可以改变原结构的自振频率和基本振型,减小振幅,避免结构的共振效应,有效提高结构的抗震能力。
自PALL等[3]提出Pall摩擦阻尼器以来,许多国内外学者对此进行了研究改进。FILIATRAULT[4]对设置Pall摩擦阻尼器的3层钢框架进行了振动台试验,试验过程中Pall摩擦阻尼器表现出稳定的性能并且有效减小了地震效应。CHERRY等[5]对文献[4]的试验结果进行了理论分析,研究了附加Pall摩擦阻尼器的最优滑动荷载,并给出适用于Pall摩擦阻尼器的最优滑移荷载谱。PAPADOPOULOS等[6-7]把Pall摩擦阻尼器改进为转动摩擦形式的X形支撑摩擦阻尼器并对此做了单榀框架试验,试验结果表现为理想的库伦摩擦滞回性能,同时对一个五层二维混凝土框架结构进行了Pushover分析,结果表明附加支撑之后框架结构的侧向刚度有所增加,有效地减小了结构的非线性位移。吴斌等[8]提出了T形芯板摩擦阻尼器,并进行了试验研究,结果表明阻尼器起滑后恢复力不变,而支撑的拉力增加较明显。王春波[9]研究了支撑在十五层框架结构中的三种不同布置方式,结果表明摩擦耗能支撑布置在结构剪切变形较大的楼层时,减震效果良好。张敏等[10]采用SAP2000有限元软件对摩擦阻尼器在框架结构内的三种对称布置方案、两种非对称布置方案进行了地震作用下的分析,模拟结果表明阻尼器对称布置时,减震效果大致相同,结构扭转效应较小。隋伟宁等[11]对一个满布摩擦阻尼器的五层钢框架进行了多遇及罕遇地震下的抗震性能分析,结果表明转动摩擦阻尼器的耗能效果良好。
本文在课题组杨小琦等[12]对转动摩擦阻尼器不同摩擦片材料的试验研究及理论分析的基础上,针对带有转动摩擦阻尼器的高层钢框架进行弹塑性时程分析,研究了钢框架的层间位移、顶点位移、顶点加速度和柱底剪力的时程变化等抗震性能。
1 钢框架模型
1.1 钢框架设计
建立16层钢框架结构计算模型,横向纵向均为三跨,跨度为7.2 m,取其中一榀进行分析。1层层高4.5 m,2—16层层高3.9 m。表1为钢框架结构的梁、柱初选截面尺寸。结构抗震计算按8度设防,场地类别为Ⅱ类,设计地震分组为第二组。

表1 钢框架截面尺寸
运用PKPM结构计算软件对框架进行初步的内力计算,主要考虑恒载、活载、风荷载以及地震作用四种荷载效应组合。其中恒载取5 kN/m2,活荷载取2 kN/m2,并按照跨度7.2 m转化为线荷载添加在结构模型上。基本风压取0.45 kN/m2,修改PKPM中风压基本信息并进行运算。图3为结构计算模型几何尺寸及内力计算结果,最大应力比为0.81。图3柱子左侧三个数字由上到下分别表示强度计算应力比、平面内稳定应力比、平面外稳定应力比。梁的上下两侧的数字分别代表整体稳定应力比、剪应力比。
1.2 有限元模型
在框架结构中,中心支撑是常用的一种支撑类型,考虑到与阻尼器的连接以及结构的对称性,避免扭转效应,因此选用人字形支撑布置在框架的中间跨。根据文献[13],消能部件宜设置在结构变形较大的位置,阻尼器布置应考虑建筑使用功能、经济性等因素采用合理布置方案。根据楼层高度确定图4所示5种转动摩擦阻尼器布置方案,11个有限元计算模型。图4(a)为钢框架结构计算模型,图4(b)(d)(f)(h)(j)为结构柱间支撑布置计算模型,图4(c)(e)(g)(i)(k)为结构转动摩擦阻尼器布置计算模型。采用SAP2000分析软件自带的截面校核功能验证得到柱间支撑截面,见表2。

表2 柱间支撑截面
图5(a)为带有转动摩擦阻尼器的钢框架,阻尼器与框架梁通过两侧的连接件连接,支撑与阻尼器通过中间的连接件连接。图5(b)为转动摩擦阻尼器在有限元模型中的模拟,①②为linear单元,模拟图5(a)中转动摩擦阻尼器与框架横梁之间的连接件;③为Damper-Friction spring单元,模拟图5(a)中转动摩擦阻尼器。图6为该单元的滞回性能,该单元考虑了摩擦阻尼器的最大滑动位移。K1为加载-滑移时单元的线性刚度,K2为卸载-滑移时的线性刚度,K0为加载与卸载之间的弹性刚度;ds为锁止位移,所有超过ds的变形使用弹性刚度K0。
定义转动摩擦阻尼器水平方向的非线性参数如下[12]:初始(非滑移)刚度为800 000 kN/m,加载滑移刚度为300 000 kN/m,卸载滑移刚度为200 000 kN/m;预压位移为0 mm,终止位移为30 mm。
1.3 塑性铰定义
SAP2000中对框架结构主要有4种塑性铰[14],钢框架计算模型梁两端指定主轴方向弯矩铰(M3),柱端指定PMM铰。塑性铰的本构模型如图7所示。塑性铰未屈服为刚性,无变形,屈服后发生塑性变形,共8种状态:A为原点;B,C,D,E分别代表塑性铰的屈服、极限承载力、残余强度和完全失效;IO,LS,CP分别对应于立即使用、生命安全和防止倒塌。
2 模态分析
定义模态分析工况,分析方法为特征值分析法,振型数量为12个。结构的固有振动特性包括周期、振型等,由于结构的低阶振型对位移和内力贡献较大[15],因此仅列出前3阶振型信息,见表3。11个模型中振型3的质量参与系数均在90%以上,满足模态分析的质量参与要求。GKJ的基本周期为2.636 s,带有转动摩擦阻尼器的模型GKJ-ZN1至GKJ-ZN5的基本周期均小于相应的带有柱间支撑的钢框架模型,且都小于无转动摩擦阻尼器的模型GKJ,这说明,安装阻尼器之后,结构刚度有所增加,摩擦阻尼器能够为结构提供一定的附加刚度。带有转动摩擦阻尼器钢框架模型的自振周期由小到大排序为GKJ-ZN4 表3 模态计算结果 根据文献[13],采用时程分析法计算结构地震作用下的动力响应,选取两组实际强震记录和一组人工模拟的地震波。对现有的强震记录,需要将其峰值加速度调整为抗震设防烈度相对应的多遇或罕遇地震时的加速度峰值。加速度峰值调整公式为 (1) 选取EI Centro波、Taft波、兰州波进行8度罕遇地震分析,调整后的峰值加速度为4 m/s2,地震波的波形如图8所示。 对模型加载以上3条罕遇地震波,通过分析层间位移、顶点位移、顶点加速度和柱底剪力等性能指标得到11个模型的地震反应。为更清楚地比较安装转动摩擦阻尼器的结构和未安装转动摩擦阻尼器的结构的地震响应,定义减震率[16]为 (2) 式中:V为减震率;Znc为无控结构地震峰值响应(位移、加速度和剪力);Zco为带有转动摩擦阻尼器钢框架结构的地震峰值响应。 限于篇幅,以下针对EI Centro波作用下结构的弹塑性动力特性进行分析。 3.2.1 层间位移曲线 图9为11个模型在EI Centro波作用下的层间位移曲线。由图9(a)(b)可知,GKJ-ZN1在1—4层的层间位移、GKJ-ZN2在1—8层的层间位移分别小于GKJ-ZC1,GKJ-ZC2在相应楼层的层间位移,未布置阻尼器的楼层层间位移增大,这说明仅在底部布置阻尼器时,底部楼层刚度较大,上部结构偏柔,导致上部楼层层间位移增大,所以这两种布置方案不合理。图9(c)中GKJ-ZN3的层间位移在2—4层略大于GKJ-ZC3,其余各层的层间位移均小于GKJ-ZC3且远远小于GKJ,所以在底部3/4楼高布置阻尼器时对层间位移的减小效果较好。图9(d)中GKJ-ZN4在11—16层的层间位移要大于GKJ-ZC4,这表明并不是转动摩擦阻尼器布置的越多减震效果就越好。图9(e)中GKJ-ZN5的层间位移呈现波动变化,这是由于隔层布置阻尼器导致相邻两层刚度相差较大。图9(f)为GKJ-ZN1至GKJ-ZN5的层间位移曲线对比,可见GKJ-ZN3,GKJ-ZN4的层间位移明显小于其余模型的层间位移。 3.2.2 顶点位移时程曲线 图10为11个模型在EI Centro波作用下的顶点位移时程曲线。如图10(a)—(e)所示,随EI Centro波变化,GKJ-ZN1至GKJ-ZN5顶点位移变化幅度明显小于GKJ-ZC1至GKJ-ZC5;由图10(f)可知,GKJ-ZN2及GKJ-ZN3的顶点位移值相对较小。 3.2.3 顶点加速度时程曲线 图11为11个模型在EI Centro波作用下的顶点加速度时程曲线。如图11(a)—(e)所示,当输入地震加速度波时,GKJ-ZN1至GKJ-ZN5的顶点加速度与GKJ及GKJ-ZC1至GKJ-ZC5的顶点加速度时程曲线趋势相近;由图11(f)可知,各方案的顶点加速度时程曲线变化趋势相差不大,这说明改变阻尼器布置方式对顶点加速度的影响并不明显。 3.2.4 柱底剪力时程曲线 图12为11个模型在EI Centro波作用下的柱底剪力时程曲线。如图12(a)所示,在EI Centro波作用时,GKJ-ZN1在6~7 s内的柱底剪力值大于GKJ-ZC1,这说明在该方案下阻尼器在结构中起到的作用略小于支撑起到的作用;如图12(b)—(f)所示,GKJ-ZN2至GKJ-ZN5的柱底剪力明显小于GKJ-ZC1至GKJ-ZC5且远小于GKJ,这说明阻尼器可以减小原结构受到的剪力,从而降低原结构的柱底剪力值。 3.2.5 减震率 表4为带有转动摩擦阻尼器的模型分别在EI Centro波、Taft波、兰州波作用下层间位移、顶点位移、顶点加速度和柱底剪力的减震率。 对于层间位移,GKJ-ZN1,GKJ-ZN2在EI Centro波、Taft波的影响下减震率为负值,这说明最大层间位移有所增加,转动摩擦阻尼器布置在1/4及1/2楼高这两种方案效果不佳。在EI Centro波作用下,GKJ-ZN3,GKJ-ZN4的减震率分别为46.47%,50.54%,优于其他模型的减震率;在Taft波作用下GKJ-ZN4减震率最大;在兰州波作用下GKJ-ZN5减震率最大。在不同地震响应下阻尼器的减震效果也不一样。 对于顶点位移,在EI Centro波作用下,GKJ-ZN1减震率最低,为6.21%,GKJ-ZN3,GKJ-ZN4的减震率相对较高,在40%左右;在Taft波作用下,GKJ-ZN1,GKJ-ZN5的减震效果较好,减震率在20%左右;在兰州波作用下,各模型的减震率在50%左右,其中GKJ-ZN5的减震率最大。 对于顶点加速度,在三种地震波的作用下,GKJ-ZN1,GKJ-ZN2,GKJ-ZN3的顶点最大加速度均有不同程度放大。可见,转动摩擦阻尼器对结构的加速度的控制效果不明显,且远小于对结构层间位移的控制效果。因此在确定阻尼器的布置时,一般以层间位移为指标。 对于柱底剪力,在EI Centro波作用时,GKJ-ZN5的减震率相对较大;在Taft波作用下,GKJ-ZN1减震率相对较高;在兰州波作用下,GKJ-ZN5减震效果最好,减震率达到65.36%。 通过对以上时程曲线及减震率的分析可以看出,阻尼器对位移的减震效果优于其他动力特性指标。因此根据层间位移曲线及减震率的分析,得到转动摩擦阻尼器在框架中的最优布置方案为GKJ-ZN3。 通过分析,输出了GKJ和阻尼器最优布置方案GKJ-ZN3在EI Centro波作用下的塑性铰发展情况。如图13所示,随地震波的输入,GKJ中部分框架梁应力梯度不断增加,直至达到屈服强度形成塑性铰。在4.6 s时,首先6—10层第一跨和第二跨的钢梁出现塑性铰,最后,除顶部4层及底层钢梁外,其余各层框架梁均达到屈服强度出现塑性铰。如图14所示,在EI Centro波作用下GKJ-ZN3塑性铰的发展明显慢于GKJ,在12.2 s时,13层第一跨的钢梁首先达到屈服强度出现塑性铰,直到地震作用结束,其余各层均未屈服,整体框架处于弹塑性状态。可见,转动摩擦阻尼器在地震作用下可以消耗大部分能量,延缓主体框架的破坏。 1) 在8度罕遇地震作用下,带有转动摩擦阻尼器结构计算模型的层间位移明显减小,但顶点最大加速度有放大趋势,转动摩擦阻尼器对位移的控制效果优于对加速度的控制效果。 2) 在距底层3/4高度安装转动摩擦阻尼器的结构计算模型GKJ-ZN3,与其他结构计算模型相比,其整体刚度和抗震能力有明显提高。 3) 转动摩擦阻尼器可以通过自身的摩擦作用消耗大部分地震输入能量,减缓钢框架结构构件的塑性变形及塑性铰发展。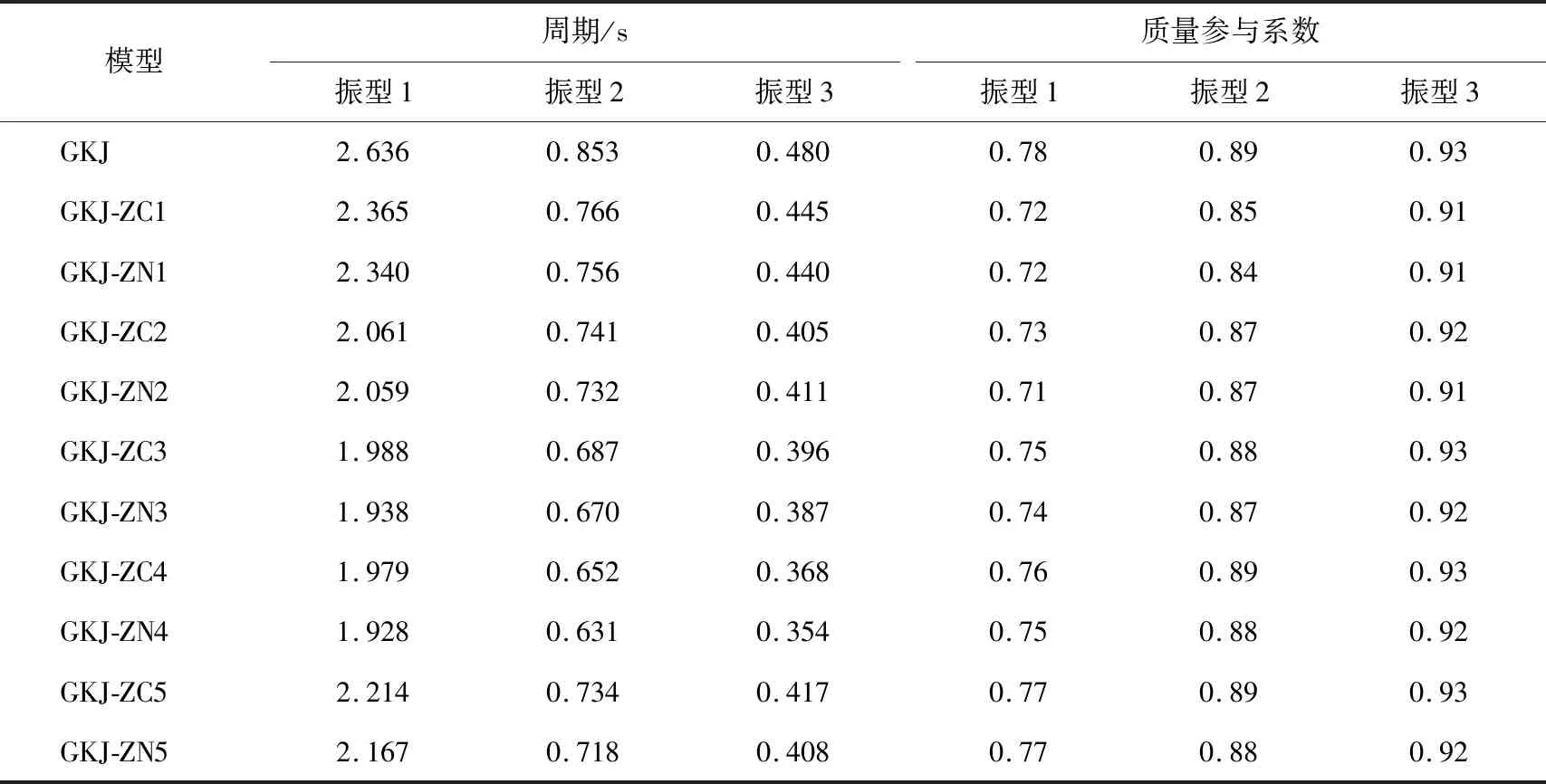
3 弹塑性时程分析
3.1 地震波的选取
3.2 弹塑性时程分析结果
3.3 塑性铰分布
4 结论
