“悬念式”教学法在线性代数教学中的应用探讨＊——以克拉默法则为例

陈礼生 黄 丽 李 佼 刘士官 任思源

（贵州民族大学材料科学与工程学院，贵州 贵阳 550025）

线性代数和高等数学是大学数学中最重要的两门基础课程，与高等数学相比，线性代数内容相对较少，里面涉及到的公式也较为简单，但是线性代数比高等数学更为抽象[1，2]，里面知识点之间的联系也更加紧密，很多学生往往很难理解其中的诸多定理和推论，从而导致学生对线性代数的学习积极性不高，甚至有些学生厌倦和恐惧这门课程。因此，老师如何教好、学生如何学好线性代数是大学数学教学过程中需要关注的核心问题。

一、“悬念式”教学法在线性代数教学中应用的重要性

线性代数是以向量、线性空间、线性方程组和线性变换作为研究对象的一门学科，可用它来研究许多复杂的线性和非线性问题，因此有人认为线性代数是许多近、现代数学分支的共同基础[3]。开设这门课是为了让学生在深入理解线性代数基础知识的同时，还能够提升学生的逻辑推理能力、应用线性代数解决实际问题的能力以及抽象思维能力等。但是在这门课程里会涉及到很多新概念，例如逆序数、余子式、矩阵、初等变换、向量组的秩、线性表示、线性相关、基础解系、相似矩阵、二次型、线性空间和线性变换等，并且还有很多定理和推论。线性代数各知识点前后联系非常紧密，并且相互渗透，环环相扣，从而使得解题方法多种多样[4]。但如果其中某个概念没有弄懂或某个推论没有深入理解，那么后面的性质或者推论就可能不会证明，从而在后期线性代数的学习过程中会产生一系列不良的连锁反应，最终会影响学生学习的热情和积极性。为了能够加强学生对线性代数知识点的理解，提升学生自学能力，激发他们的学习热情和积极性，在教学过程中采用“悬念式”教学法显得非常有必要。所谓“悬念式”教学法就是在学习新知识点之前或者在讲完某一知识点之后，提出引人入胜的问题，让学生在课前或者课后去思考和研究，然后在下次上课时师生一起共同讨论和解决。通过连续不断地去巧设疑问、引入新知的链式教学法来让学生进行头脑风暴，碰撞出智慧的火花，使他们对线性代数产生浓厚的学习兴趣[5，6]。“悬念式”教学法是培养创新人才和创新精神的重要手段，是提升学生学习积极性，提高教学质量的重要途径[7-9]。本文就以克拉默法则为例来探讨“悬念式”教学法在线性代数教学中的应用，以期提升学生学习的积极性和自学能力。

二、“悬念式”教学法在线性代数教学中的应用——以克拉默法则为例

1.巧设问题

在《经济应用数学基础（二）线性代数》第五版教材中，第一章第五节就已经讲到了克拉默法则，里面对于克拉默法则的定义介绍如下：

含有n个方程的n元线性方程组为：

将线性方程组（1）中未知数前面的系数按顺序排列，组成系数行列式D，当D≠0时，线性方程组有解，并且解唯一：

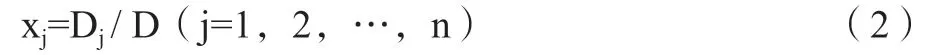
其中Dj（j=1，2，…，n）是用常数项b1，b2，…，bn分别取替换D中第j列元素a1j，a2j，…，anj后所得到的行列式。

书上对于克拉默法则的证明是运用了行列式、代数余子式和行列式按行（列）展开等知识。具体证明过程如下：

证：以行列式D的第j（j=1，2，…，n）列元素的代数余子式A1j、A2j、……，Anj分别乘方程组（1）中的第1个，第2个，…，第n个方程，然后相加，得

根据1.4节中定理1.4可知： D= a1jA1j+ a2jA2j+ … + anjAnj（j=1，2，…，n），因此（a1jA1j+ a2jA2j+ … + anjAnj）xj=D xj。根据定理1.5可知：0= a1jA1t+ a2jA2t+ … + anjAnt（j≠t），因此等式（3）等号左端，除了（a1jA1j+ a2jA2j+ … + anjAnj）xj=D xj，其余项都为0。方程（3）中等号右端等于以常数项b1，b2，…，bn分别取替换系数行列式D中第j列元素后所得到的行列式Dj，即

如果线性方程组（1）有解，那么它的解一定会满足方程组（4），而当系数行列式D不等于0时，方程组（4）只有形如式（2）的解：

xj=Dj/D（j=1，2，…，n）

另一方面，将式（2）代入方程组（1）中，可以验证它一定满足（1）式，所以式（2）是方程组（1）的解。综上所述，可得：当方程组（1）的系数行列式不等于0时，有且仅有唯一解[10]：

xj=Dj/D（j=1，2，…，n）

通过对克拉默法则证明过程的分析可以发现，此处证明主要是应用到了《经济应用数学基础（二）线性代数》第五版教材里1.4节中的定理1.4和1.5，然而克拉默法则的证明方法有多种，为了能够让学生打开脑洞，点燃智慧的火花，在此处可以通过“悬念式”教学法巧设几个问题：除此之外，是否还有其他的新解题方法？如果有，需要用到哪些知识点？问题提完之后就鼓励大家先一起预习第二章《矩阵》的内容，这个问题可以等我们学习完逆矩阵之后再一起来进行讨论。

2.引入新知

等到学习第二章逆矩阵的内容之后，再一起来回顾上次所提的问题，除了应用《经济应用数学基础（二）线性代数》第五版教材里1.4节中的定理1.4和1.5之外，是否还有其他解题方法？先让学生们思考十分钟，在思考期间，通过引导学生利用新学的知识点来解答问题。十分钟后，让学生主动来回答问题，然后我们再一起来分析证明，证明完之后再一起来总结两种证明方法所用到的知识点。

新方法就可以利用逆矩阵的知识点来进行证明，具体证明过程如下：

证：把方程组（1）写成矩阵方程

这里A为矩阵方程的系数矩阵，由于A为n阶方阵，并且|A|≠0，所以A-1存在。

在（5）式等号两边同时右乘A-1，则有：

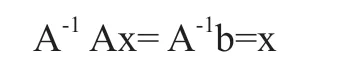
由于逆矩阵具有唯一性，因此A-1b=x是方程组（1）的唯一解向量[3]。

亦即

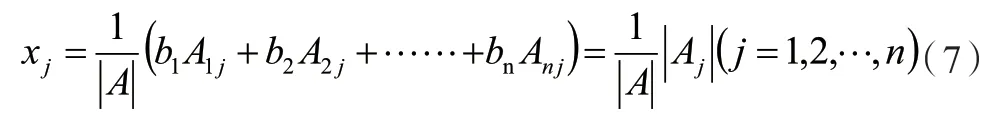
方程（7）中|A|和|Aj|即分别为方程式（4）中行列式D和Dj，因此即可证明克拉默法则。

在用以上两种方法来证明克拉默法则的过程中，用到的知识点包括：行列式按行（列）展开的定理和推论、矩阵的乘法运算、伴随矩阵和逆矩阵的求法等。

3.经典示例

为了加深学生对克拉默法则的理解，检查自身的学习效果，提升学生分析问题和解决问题的能力，并且达到查漏补缺的目的，在讲完克拉默法则证明过程之后，应该适当引入经典例题来对知识点进行巩固。因此可以结合同济大学《工程数学：线性代数》第六版45页中的例题16和《经济应用数学基础（二）线性代数》第五版29页中的例题2来进行具体讲解，以提升学生们应用克拉默法则来求解线性方程组的能力。

4.自主探索

通过合作交流，引导学生自主建构，同时注重情感激励，建立和谐的师生关系来营造自主探索的氛围，从而激发学生的自主探究兴趣。克拉默法则的证明过程不止这两种方法，课堂结束后，会适当留白，让学生们带着疑问去一起讨论和思考[11]，或者鼓励他们通过上网和查文献等方式来自主探索克拉默法则的其他证明方法，然后在下一次上课的时候，一起分享各自的证明方法。对于正确的证明方法，可以给与适当的表扬和鼓励，对于欠妥的方法，可以指出其中的漏洞，并提出纠正思路。这种方式不仅能够激发他们对线性代数学习的激情，而且还能提升学生们的团队协作能力和自学能力。

5.总结归纳

归纳总结是“悬念式”教学过程中非常重要的一个环节，它要求教师在一堂课结束前或某个知识点讲完之后，引导学生一起对知识点、解题过程和方法进行归纳总结，在总结时需要结合课程目标来进行，比如要体现过程和方法目标的实现，体现知识与技能的要求等；同时还要注重学生的学习反思，最后要求以疑引新。线性代数这门课程涉及到的知识点非常多，并且各知识点之间的联系非常紧密，往往会出现有些题目的解题方法多样，比如逆矩阵的求法，不仅可以通过逆矩阵的定义和逆矩阵的计算公式来进行求解，还可以通过初等变换等方法来求出逆矩阵；又如二次型不仅可以通过正交变换法将其化成标准形，而且还可以通过配方法将其化成标准形。因此，本文虽然仅以克拉默法则为例探索了“悬念式”教学法在线性代数教学中的应用，但是为了能够提升学生的学习积极性，提高教学质量，在线性代数这门课程中，还有许多知识点仍然需要用到“悬念式”教学法，甚至有必要将这种教学方法贯穿于整门课程之中。在通过“悬念式”教学法讲授完某个知识点之后，可以适当结合某些经典例题来对知识点进行巩固，然后再与同学们一起来总结归纳例题中所运用到的知识点、结题过程和方法，最后提出新的疑问来引出新的知识点。

结语

线性代数这门课程里面的新概念、定理、推论和计算都非常多，如果仍然利用传统案例式教学方法来讲授课程，在这有限的32或48个学时内，学生很难深入理解全部的知识点，从而影响他们学习的积极性。而利用“悬念式”教学法来开展线性代数课程的教学，教师在此扮演的角色就不仅仅是授课者，而且还是学生的组织者、合作者和引导者，学生则是学习的主人，教师通过组织和引导学生来学习线性代数，不仅能调动学生学习的积极性，提升教学质量，而且还能逐渐培养他们的深入思考问题、举一反三和团队协作能力。