非凸环境下基于约束控制的机器人集群算法*

曹 凯，陈阳泉，高 嵩，党海鑫，张嘉豪

(1.西安工业大学 机电工程学院，西安 710021； 2.西安工业大学 电子信息工程学院，西安 710021；3.加州大学默塞德分校 工程学院，默塞德 95343)

多机器人系统因其并行性高，灵活性强，相对于单机器人而言效率更高，已逐步应用于军事、救援、环境覆盖等领域中更加复杂的任务场景，具有很强的研究意义与广泛的应用前景[1-2]。目前在该领域已经有了多种控制机器人集群在环境中分布的方法，如虚拟物理力法[3]、随机有限状态机[4]，以及质心维诺算法(Centroidal Voronoi Tessellation,CVT)[5]。其中CVT算法最大特点是利用维诺划分对联合感知任务进行解耦，实现了待优化目标函数的分布式计算[6]。根据CVT的固有属性，该算法能够保证机器人之间碰撞问题。文献[7]将无人机集群应用于喷洒农药等农业应用，CVT算法给无人机提供最佳的位置分布，以最大的效率对农作物进行药物喷洒。上述这些分区划分必须保证环境区域严格为凸环境，但是实际中常见的环境中大多为非凸区域，在很大程度上限制了机器人集群的应用场景，因此如何解决非凸问题下的多机器人控制是学者们目前的重要研究方向之一[8-9]。

为了消除多机器人集群在非凸环境下的局限性，文献[10]中利用旅行商算法结合区域内路径规划问题将非凸多边形区域分解为多个凸多边形环境，将多个凸多边形进行快速的覆盖已完成非凸区域的覆盖问题。文献[11]将Lloyd算法和路径规划算法相结合，由机器人位置得到一个不考虑障碍物的凸形环境目标点，计算目标点对应于障碍物的投影点，将其设为目标进行跟踪，并使用TangentBug算法提供了避障行为，引导机器人绕过障碍物，最终完成集群机器人在非凸环境下的覆盖。文献[12]使用测地距离来代替欧几里得距离确定维诺细胞，并结合功率图对环境中机器人的权重进行平均划分。然而，这种方法涉及计算困难的几何计算，导致其难以应用于实时控制的多机器人系统，并且仍然限于具有多边形障碍的欧几里得环境。文献[13]通过改变机器人的控制率，使得CVT应用在在非凸环境中，将非凸点和代价函数相结合，最小化机器人系统的代价函数，使得集群机器人使用CVT算法可以完成任意环境的覆盖。文献[14]基于对覆盖范围函数的最小化来概括控制律，以适用于非凸空间环境，并结合图搜索算法解决球面和具有障碍物的圆环上的最优覆盖问题。

集群机器人在实际运行过程中会受到各种影响因素，为了保证水下机器人推进器运行的稳定性与可靠性，文献[15]提出了一种状态评估方法，经过BP神经网络计算出推进器的健康度。当机器人规划路径中需要较大程度的拐弯等动作时，可能导致机器人运动速度、加速度过大时，需要对其做运动学约束、物理约束等约束，充分保证轮式移动机器人自主行驶的可行性，安全性，高效性。模型预测控制是近年来被广泛讨论的一种反馈控制策略，该方法在生成轨迹时会实时处理各类约束，在轨迹跟踪时表现良好的性能[16]。因此，文献[17]使用CVT算法将无人机系统部署在每个维诺细胞的质心位置，将系统模型中的噪声以及外界风速的影响作为模型预测控制(Model Predictive Control,MPC)的约束，对无人机系统做出状态估计，最终得到可行轨迹。

文中针对非凸局限性和质心不可达问题，提出了基于二次约束的CVT算法，使得机器人产生的维诺区域不与非凸环境重叠，将维诺细胞质心约束在可达区域内。为了优化机器人运动轨迹设计了模型预测控制器，进一步保证机器人的安全。以常见的凸环境和非凸环境为例，验证文中算法在非凸环境下划分的有效性并做出对比分析，以比例积分控制器和文中设计的模型预测控制器在机器人轨迹异常时的控制结果为对比。以5台Turtlebot3机器人来验证机器人集群算法，仿真对比验证本文算法的有效性。

1 质心维诺划分局限性描述

1.1 质心维诺划分算法与非凸环境

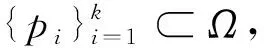
zi={q∈Ω|‖q-pi‖≤‖q-pj‖,

1≤j≤k,j≠i}，

(1)

其中相邻的维诺细胞之间不重叠。每个维诺细胞中有且只有一个生成点，所有的维诺细胞之和就是整个环境区域。根据维诺图的特性，当机器人作为维诺细胞的生成点时，只要保证机器人尺寸小于维诺细胞，机器人之间不会发生碰撞。

假设区域Ω的密度函数定义为ρ(q)≥0，每个Voronoi细胞的质心定义为

(2)

在维诺划分的过程中，Lloyd算法保证生成点不断更新并移动到维诺细胞的质心位置，整体的代价函数为

(3)

区域是几何学的基本概念之一。对于按照几何形状来划分，任务环境可以分为凸型和非凸型区域。若区域中任意两点连线不全在区域内，则为非凸区域。图1(a)中圆形将平面分为两个区域，其中只有一个凸区域(圆形的内部)，外部平面即为非凸区域，即经过圆形区域部分的直线和区域不存在公共点，所以图1(a)为非凸区域。图1(b)中，环境区域的凹陷使得该区域为非凸区域，在区域凹陷处的上下部分取一点，所连接的直线段并不能保证所有的点仍在该区域内。

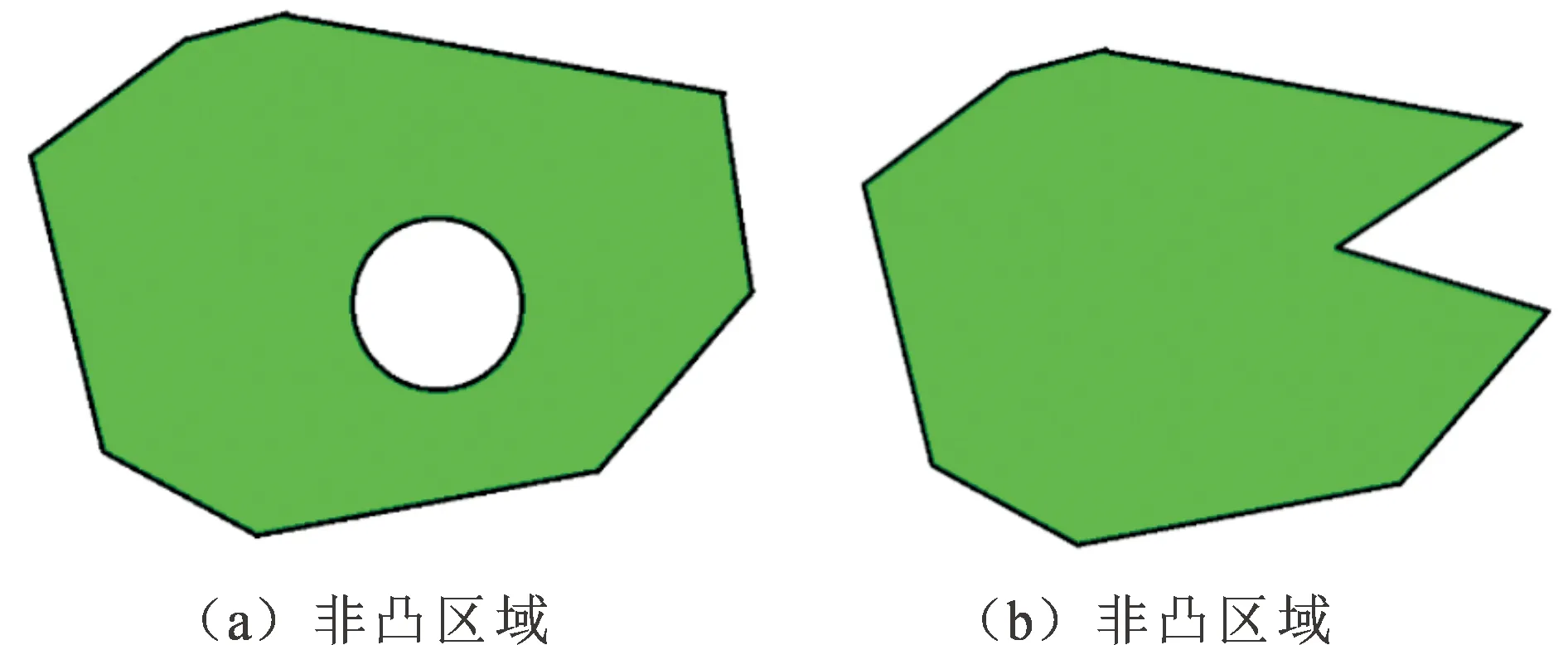
图1 非凸任务区域环境

在凸型区域环境的质心维诺划分中，基于Lloyd算法能够保证生成点收敛至对应的质心位置。相对于严格的凸区域，实际环境中更常见的是非凸型区域环境，质心维诺划分算法对于非凸形区域环境，存在一些局限性。如图2所示，给出了在不同环境下的划分情况。根据对不同环境的划分，对质心维诺划分算法的局限性进行分析。

图2 非凸区域划分存在的问题

在图2(a)所示的凸环境中随机生成10个生成点，图中用圆圈所示，根据Lloyd算法，生成点最终收敛到各自细胞质心位置，均匀分布在环境区域内部。得到如图2(a)所示的分布情况。在图2(b)所示的非凸区域环境中，内部存在障碍物导致环境区域为非凸环境，此时对存在障碍物的环境进行质心维诺划分，其质心可能会生成在障碍物中，如图2(b)中红点表示维诺细胞的质心位置，当存在质心位置在障碍物内的情况时，如果机器人将质心位置作为下一时刻的目标，则机器人便会与障碍物发生碰撞。在图2(c)所示的非凸区域环境中，环境中并没有障碍物，但环境外部区域存在凹陷，此时环境区域也为非凸区域，当进行维诺划分时，质心位置会出现在环境外部，若下一时刻机器人运动到质心位置，则会运动到环境区域外部，即与环境发生碰撞。

通过上述分析，考虑到如果要将集群机器人应用在非凸环境中，则必须要保证两个基本问题为：障碍物内不能有划分的维诺细胞；每个维诺细胞质心不能在障碍物内。若对维诺细胞以及质心的位置进行严格约束，不仅能保证机器人之间、机器人与环境之间的安全，还可使的机器人在跟随相应质心对环境进行覆盖时严格位于环境区域内部。

1.2 机器人轨迹规划中相关约束的数学描述

为了简化控制器的设计，本文以使用的差速两轮机器人为例，并假设轮式移动机器人整体为一个可以自由转动的刚体，其简化的运动学模型如图3所示。

图3 机器人运动学模型

设定x为横向坐标，y为纵向坐标，θ是方向角。机器人的状态信息用p=(x,y,θ)T来表示。[v,ω]T为机器人的线速度和角速度。2L为两轮之间的长度，2r为轮子的直径。运动学状态空间方程为

(4)

随着工业自动化程度的提高，对机器人也提出了越来越高的要求，机器人的任务也越来越复杂，控制要求也更加严格。实际环境中机器人运行会受到各种影响因素，如任务环境崎岖不平，机器人规划路径中存在较大程度的拐弯等现象，这些现象在以前的任务中可能被忽略。若机器人运动速度、加速度过大，为保证机器人的安全，需要对机器人运行过程做出约束和限制，以保证机器人的安全。针对上述问题，本文对基于CVT算法的参考轨迹进行模型预测控制，提高集群机器人运行的安全性。

考虑到运行安全性，往往要求线速度v和角速度ω小于一定值，假设最大线速度和最大角速度分别为vmax和ωmax，最小线速度和最小角速度分别为vmin和ωmin，则该约束形式为

(5)

2 非凸环境中的机器人集群控制

2.1 基于二次约束的CVT算法

假设机器人集群中机器人i对应的环境维诺细胞为zi,i=1,2,…,k，环境中的障碍物区域为wi,i=1,2,…,k，为了保证维诺细胞中不包含障碍物，则机器人对应的维诺细胞被约束为

Zi=zi-wi,(i,j=1,2,3…,k)。

(6)

若环境中并无障碍物或环境为严格的凸环境，则w=0，维诺细胞不发生改变。当维诺细胞中存在障碍物时，维诺细胞会将障碍物区域的边界作为内边界，重新定义维诺细胞。

在保证了每个维诺细胞都在环境内后，考虑到在非凸环境内得到的质心位置可能出现在区域外面的问题，本文对质心位置进行二次约束。即将维诺细胞的质心严格约束在维诺细胞内，表示为

(7)

若没有得到该约束解，则该维诺质心不更新，直到其他维诺细胞发生变化从而影响该维诺细胞质心位置在维诺环境内后，质心重新开始更新迭代，直至算法收敛。

二次约束下的质心维诺划分算法主要思想如下：在环境细胞内，随机生成k个生成点。首先，计算每个生成点的维诺细胞，并判断障碍物与维诺细胞否有交集，若不存在交集，则维诺细胞内没有障碍物；若有交集，则将障碍物的边界作为维诺细胞的边界，更新该生成点的维诺细胞。其次，计算每个维诺细胞的质心位置，并判断质心位置是否在维诺细胞内。若不在，则重新计算维诺细胞；若质心在维诺细胞内，则将生成点更新至质心位置，直至算法收敛。二次约束下的质心维诺划分算法具体过程见表1。

表1 二次约束下的质心维诺划分算法

2.2 模型预测控制器设计

图4中给出了使用质心维诺划分算法结合Model Predictive Control,MPC的机器人集群系统体系结构。

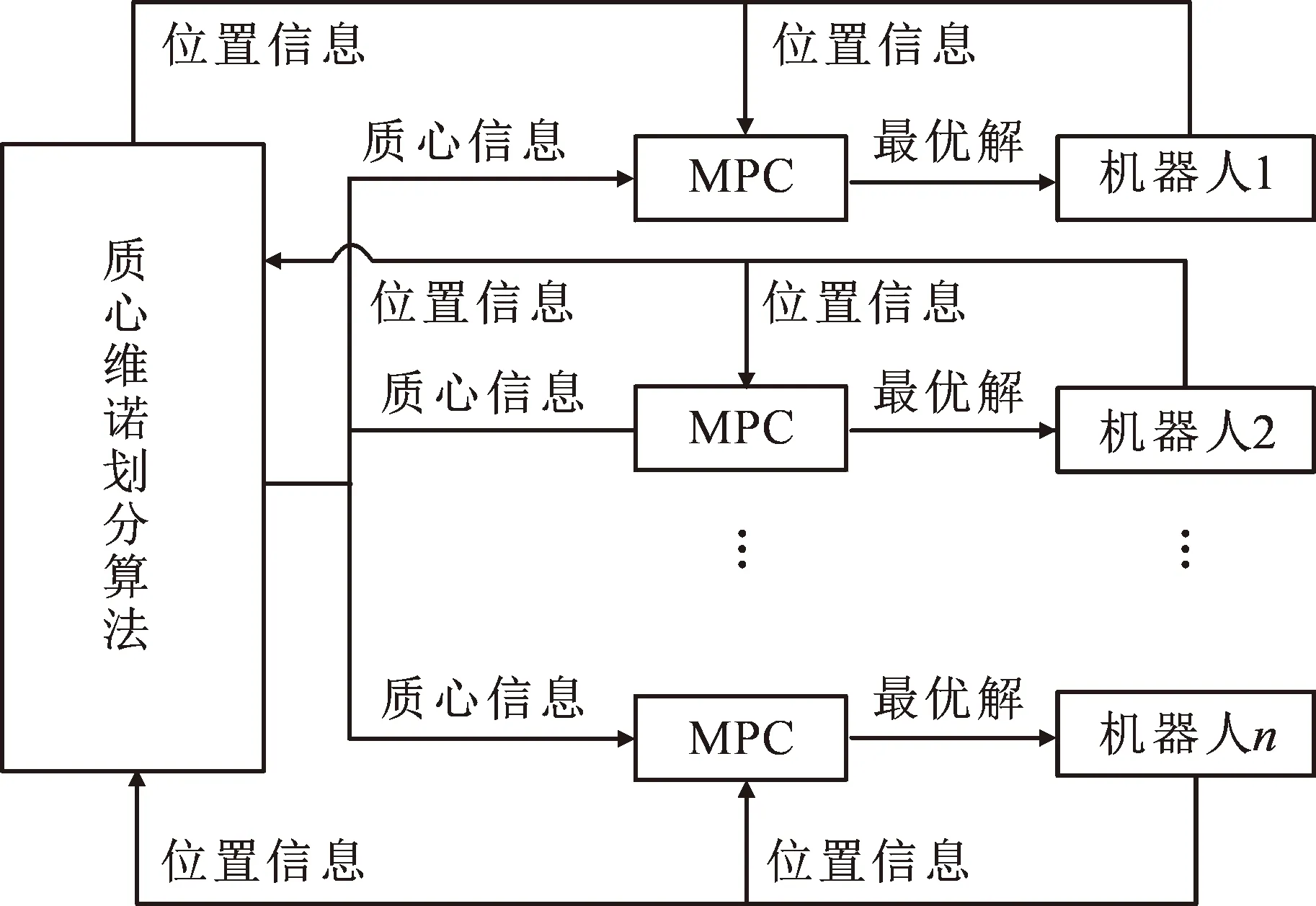
图4 CVT结合MPC的机器人集群系统结构图

由图4可以看出，MPC在得到机器人当前状态信息和每个维诺细胞的质心位置后，求解满足设定目标函数以及约束二次规划问题，并将得到的控制序列中第一个元素作为机器人的实际控制量作用于对应的机器人，直至算法迭代至收敛，则控制结束。

根据机器人的运动学状态空间方程，假设机器人的实际位姿为p=[x,y,θ]T，实际速度[v,ω]T，即

(8)

其中x和u分别为机器人的位姿和速度，则可得到

(9)

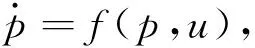
(10)

(11)

离散化模型为

(12)

式中：pk为机器人当前状态变量；uk为对机器人的控制输入变量；yk为被控输出变量。最后使用前向欧拉进行离散化可得到

其中T为控制周期，进一步改uk为控制量增量表达式。设

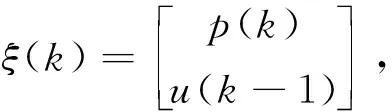
(13)

Δu(k)=u(k)-u(k-1)，

(14)

则可以得到新的状态表达式为

(15)

从式(15)中可以体现出使用当前状态和当前输入预测下一时刻状态，新的系数表达式为

预测时域内的系统输出量为

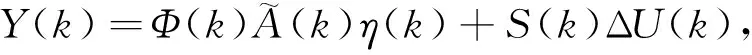
(16)

将式(16)展开，其中

式中：p′为预测时域；c为控制时域。进行轨迹跟踪时期望和预测的轨迹具有较高的重合度，因此常通过目标函数来表示轨迹重合情况，最终得到的目标函数值越小表示两条轨迹的重合度越高。因此将轨迹优化问题转化为求目标函数最小值的问题，这里选取目标函数为

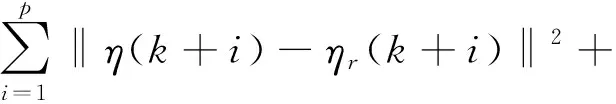
(17)

式中：ρ为权重系数；ε为松弛因子。

将式(17)转化为式(18)的形式，

(18)

将式(17)代入式(18)代价函数表达式中，得到

(19)

其中

(20)

式中：Γy和Γu分别为输出和输入误差的加权矩阵；ek为预测时域内的跟踪误差。在对上式求解后，可以得到

(21)

将求解后的控制序列中第一个元素作为对机器人实际输入的控制量，即

(22)

机器人得到控制量后，得到新的状态量进入下一个控制周期。在目标函数最小化后可得到机器人约束轨迹。

3 仿真结果及分析

为分别验证了所提算法在凸环境和非凸环境中的适用性，仿真在Matlab中进行。在对机器人进行二阶动力学建模的基础上，使用虚拟点模拟机器人进行虚拟数值仿真。以10个机器人作为集群机器人系统。利用代价函数表示系统中每个机器人和对应维诺质心位置的误差和。若要保证集群系统稳定，误差和要趋于足够小，文中以0.001作为判定条件，判定系统是否达到稳定。

3.1 凸环境下改进CVT算法的仿真验证

以图5(a)中的场景作为凸环境的代表，对该算法进行验证。图5给出了凸环境在该算法下的最终划分结果图以及对应的机器人集群系统代价函数图。

图5 凸环境实验结果图

在如图5(a)所示的凸环境中，算法能较快的对环境进行维诺划分，此时环境中不存在障碍物等其他影响维诺划分的因素，此时改进算法中代表障碍物区域的w=0。所提算法和传统CVT算法都能对环境进行质心维诺划分，得到如图所示的机器人分布。其中不同颜色区域代表不同机器人对应的维诺细胞，即机器人在任务环境中负责的区域。

图5(b)给出了系统的代价函数，由于环境较为简单，系统达到稳定所需要的迭代次数也较小，当迭代次数为51时，系统已经达到稳定状态，机器人系统达到环境中的最优分布。根据代价函数的意义，最终系统区域稳定时的代价函数值趋于0，表示机器人位置和其对应的维诺质心之间误差足够小，认定系统达到一个稳定状态。

3.2 非凸环境下改进CVT算法的仿真验证

本节将非凸环境分为以下3种情况，第一种情况：外部边界为凸，内部含有障碍物；第二种情况：外部边界为非凸，内部没有障碍物；第三种情况：外部边界为非凸，内部含有障碍物。实验分别对3种非凸环境进行仿真及分析。

1) 内部含有障碍物

非凸环境1假设凸环境中存在一个圆形障碍物，导致整个机器人可运行的任务环境为非凸环境。

如图6(a)所示，为10个机器人在非凸环境1中的分布及各自对应的维诺细胞，算法有效地对该任务环境进行划分。在常密度函数下，机器人对除障碍物以外的区域进行维诺划分。图6(b)为集群系统的代价函数图，当迭代次数达到89次时，系统达到稳定状态。

图6 非凸环境1实验结果图

2) 外部环境为非凸

非凸环境2中外部边界为非凸，环境区域向中间凹陷。图7为10个生成点在非凸环境2中进行质心维诺分布的过程。

图7 非凸环境2下的质心维诺分布过程图

如图7(a)所示，在区域左下角随机生成10个点，橙色的圈表示生成点的初始位置，“+”代表当前时刻每个生成点对应的维诺细胞质心位置。当算法迭代次数15次，如图7(b)所示，维诺细胞A中，下一时刻区域质心在环境区域外部，生成点不能继续更新，其他维诺质心继续更新，相邻的维诺细胞在不断变化。当迭代次数为47时，如图7(c)所示，维诺细胞A的形状随其他细胞的变换而变化，此时该区域的生成点位置仍保持在区域外部。当迭代次数为48时，区域A的维诺质心位置重新生成在区域内部，如图7(d)所示，图中区域A的质心位置开始运动，算法继续迭代。当迭代次数为78时，最终形成非凸环境下的质心维诺分布。

图8为在该环境区域下系统的代价函数，图中代价函数随着迭代次数逐渐减小，最终趋于0，系统最终趋于稳定，其中当系统迭代78次时，系统中每个生成点个各自对应的维诺质心位置误差和小于0.001，认为系统达到稳定状态。

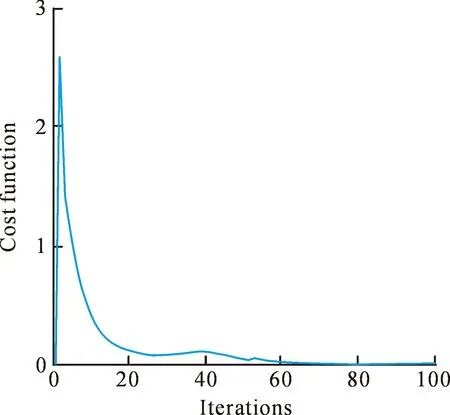
图8 机器人集群系统代价函数

3) 障碍物+外部环境为非凸

非凸环境3假设环境外部边界为非凸且内部包含障碍物。此时算法需保证质心既不能位于区域外部，也不能位于障碍物内部。最终非凸环境3的质心维诺分布如图9(a)所示，图中用区域左下角随机生成的10个橙色圆圈代表机器人的初始位置，“+”代表当前时刻每个生成点对应的维诺细胞质心位置。

在该环境中，当某个维诺细胞的质心位置出现在环境外部或者在障碍物内部时，该维诺细胞的生成点停止迭代。当算法迭代次数12次，如图9(b)所示，计算得到维诺细胞B中，下一时刻区域质心在环境区域外部，此时该区域的生成点停止更新。当迭代次数到达70次，如图9(c)所示，此时该区域的质心位置仍在区域外部，该区域的生成点位置在迭代次数12～70间都没有更新。当迭代次数为71时，区域B的维诺质心位置生成在区域内部，如图9(d)所示，图中区域B的质心位置开始运动。当迭代次数为132时，最终形成非凸环境下的质心维诺分布，如图9(e)所示。

图9 非凸环境3质心维诺分布过程图

机器人集群系统代价函数如图10所示。由于环境场景较为复杂，算法在划分维诺细胞及计算质心位置时的计算量较大，系统达到稳定状态时的迭代次数也随之增加，当迭代132次时，系统达到稳定。

图10 集群系统代价函数

表2给出了几种不同环境下，机器人集群系统稳定时需要的迭代次数对比，实验结果表明，在不同的非凸环境下，文中提出的算法最终都能对环境进行较为理想的划分，但由表2也可以看出在相同机器人数量下，凸环境场景较为简单，达到系统稳定时所需的迭代次数最小，而非凸环境3是由外部环境和内部障碍物组成的较为复杂的环境，该种情况下稳定所需的代价函数最大。即环境场景越复杂的区域，所需的代价函数越大。

表2 不同环境区域下的参数对比

3.3 比例积分控制仿真实验及分析

在10*10的仿真环境里，给出了一个非凸几何形状场景，如图11所示。

用改进后的CVT算法进行区域划分，10个机器人从非凸环境的左下角出发，黑色的点表示每次迭代过程中对应的维诺细胞质心位置，形成的轨迹为机器人参考轨迹，“o”表示机器人位置，使用比例积分控制对其进行跟踪，得到如图11所示灰色轨迹。过程中出现两次较为明显的拐点，在图11中分别用1、2进行标注。可以看到，在CVT算法计算维诺质心时得到了如图中点线所示的参考轨迹，包括在拐点处也进行了较好的跟随，大多数轨迹段都拟合的较好。出现明显拐点是因为没有考虑机器人和环境因素可能引起的安全性问题。但在实际环境中，当机器人运行到这两个拐点处，由于拐点角度过大，可能会因为其速度方向突变而引发一些不安全问题，不能保证机器人运行的安全性。

图11 基于比例积分控制的轨迹跟踪图

图12给出了图11中场景边缘处的局部放大图，可以看出，由于维诺细胞的非凸性，对应区域的质心位置会生成到环境外部，但机器人的运动轨迹如图中灰色曲线所示，并没有离开环境区域，当质心位置在环境外部时，机器人停止跟踪，直至质心位置重新回到环境内部。再次验证了改进CVT算法的有效性。

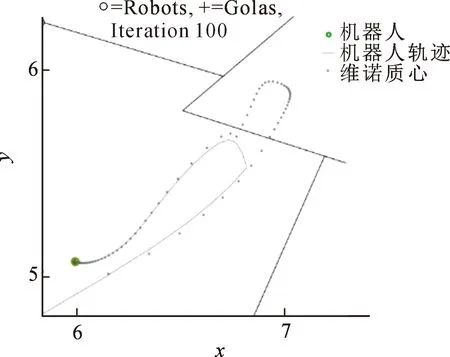
图12 场景边缘处的局部放大图

3.4 模型预测控制控制仿真实验及分析

对提出的基于CVT的模型预测控制控制进行仿真分析，并对机器人轨迹增加约束，验证本文算法的有效性。给出机器人的系统参数，见表3。在环境的左下角随机生成10个位置作为机器人的初始位置，目标位置由对应维诺细胞的质心给定，其他相关参数经过系统的不断调试，得到见表4的参数值。

表3 机器人系统参数表

表4 系统仿真参数表

为了保证机器人运行的安全性，在机器人的系统参数基础上，文中将机器人参数中最大速度的90%作为机器人的速度约束，同时对角速度也进行了限制，给出了系统的物理约束为

(23)

利用给出的约束条件进行了数值仿真，仿真结果如图13所示。

图13 基于模型预测控制的轨迹跟踪图

图中黑色的点为CVT算法给出的质心轨迹，“o”为机器人当前位置，灰色线条为MPC得到的跟踪轨迹，显然在约束了速度和角速度后，可以看出两个拐角部分相对于比例积分控制的效果更加平滑，图13中仍然使用1、2进行标记，这种更加平滑的运行轨迹更加符合机器人在环境中的实际运行情况，提高了机器人的安全性。在环境场景边缘处，改进CVT算法有也保持了自己的特性，保证机器人不会运动到环境外部。

为了更好的说明跟踪效果，将其中一条机器人轨迹跟踪结果分解为三个量(x,y,θ)进行分析，图14分别给出了三个状态量分别的控制效果，红色线条为参考轨迹，黑色线条为跟踪轨迹，从两条轨迹上看，在采样时间25 s之前的跟踪轨迹稍有波动，之后的轨迹基本重合。

图14 路径跟踪轨迹

图15给出了三个状态量的误差效果图，采样时间小于25 s时的跟踪效果的纵向位置误差范围不超过(-2 m,2 m)，θ的误差也在(-1 rad,1 rad)内，在采样时间大于25 s后，纵向位置与θ的跟踪效果更佳，最终三个量的误差基本都趋于0。

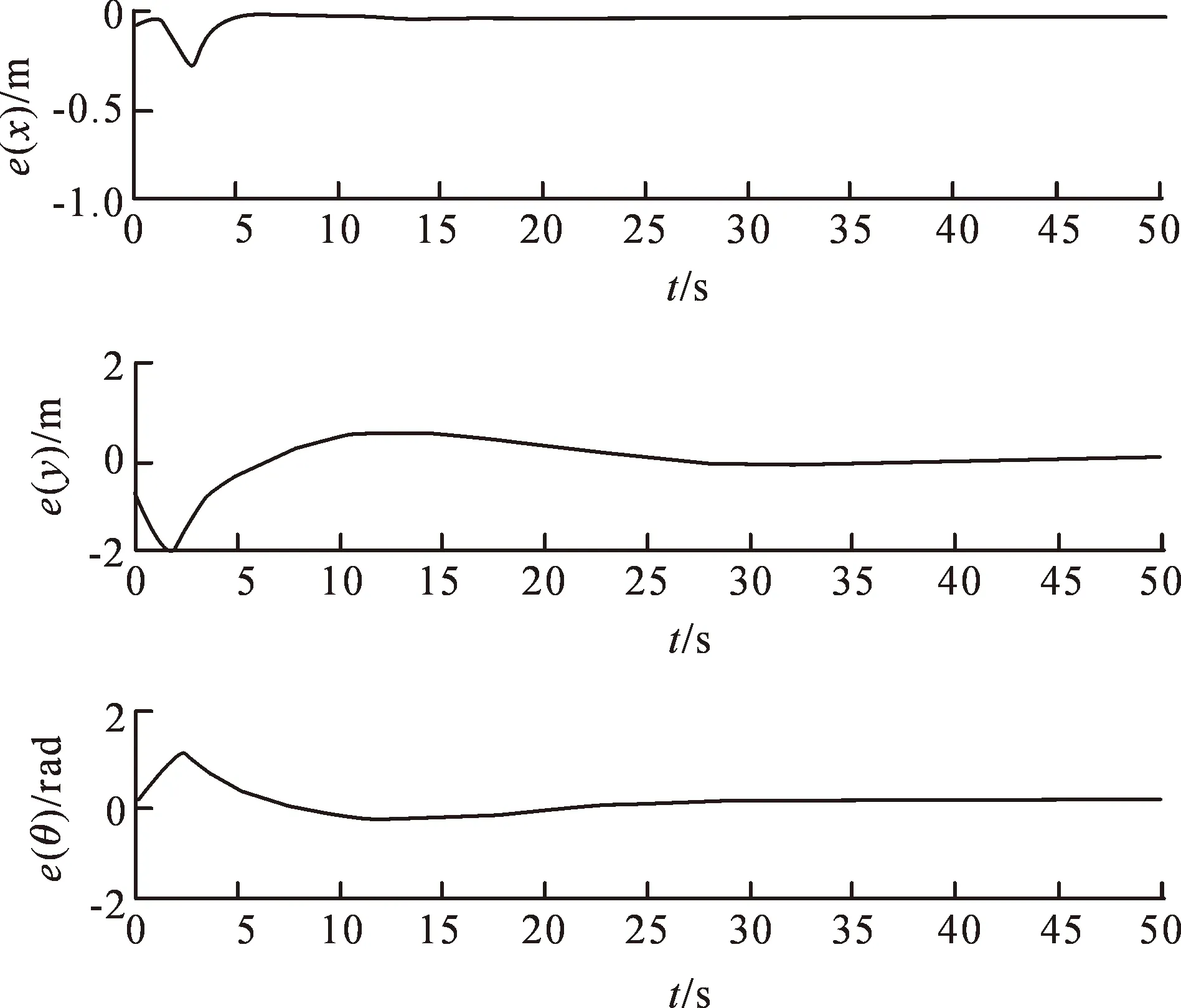
图15 路径跟踪误差

在比例控制下，机器人出现速度和角速度较大的情况，即采样时间为35 s左右时，机器人出现速度和角速度较大的情况，如图16(c)所示。在实际环境中，当机器人在跟踪轨迹的某一点出现超出限制时，在很大程度上不能保证环境中机器人的安全性；在模型预测控制的情况下，当控制量超出了约束条件范围外，则将控制量给定为最大控制量0.5 rad·s-1处，保证了控制量在约束范围内，不会出现加速度过大的现象，从而保证机器人运行时的安全性。通过对比两种情况下的机器人控制情况，可以得到本文提出基于CVT的模型预测控制能够对机器人进行速度和加速度的约束，生成符合约束条件的可行轨迹。

两种控制方法在一定程度上，都可以较好的对机器人轨迹进行跟踪，但是模型预测的路径更为平滑，为了充分说明所提算法对条件约束的处理能力，将文中2号拐点所在的路径进行再一次的分析，对比了两种控制算法中的控制量，如图16所示。

图16 控制量约束对比图(左边为比例控制，右边为模型预测控制)

4 集群机器人实验结果与分析

4.1 机器人平台简介

采用的Turtlebot3机器人是一款小型，低成本，完全可编程，基于ROS(Robot Operating System)的移动机器人。基本组件有用于驱动的舵机、运行ROS操作系统的SBC、激光雷达、用于底层控制的嵌入式开发板OpenCR，其尺寸大小为138 mm*178 mm *192 mm，是机器人体积中较小的一款产品，更利于做集群机器人研究。机器人如17图所示。

4.2 凸环境下机器人实验结果与分析

仿真为3.5 m*3.5 m的正方形场景，假设机器人为一阶动力学模型，如图18(a)中，圈表示机器人当前位置，在左下角生成5个随机点作为机器人初始位置；图18(b)为对应的实验场景，实验场景为3.5 m*3.5 m的正方形，在左下角随机摆放5台Turtlebot3机器人作为初始位置。

图17 Turtlebot3 机器人

图18 集群机器人初始位置

根据机器人当前位置，质心维诺划分算法对实验场景进行划分，得到对应的维诺细胞以及维诺细胞质心位置，在迭代25次后，得到如图19(a)所示的机器人分布情况，灰色线条为机器人运行轨迹。图19(b)为机器人集群运动过程的分布图，为了更加直观的对比仿真和实验结果，在实验场景中将维诺细胞用红的线条画出，并使用黄色的点标注出当前机器人维诺细胞所对应的质心位置，即机器人的下一个目标位置。对比两幅图可以看出，实验场景中机器人的走向以及当前位置和仿真基本一致。

图19 迭代25次时集群机器人分布

当仿真趋于稳定时，机器人位置和维诺质心位置重合，得到如图20(a)所示的机器人分布以及机器人运动轨迹，在模型预测控制器作用下，机器人运动轨迹更加平滑。图20(b)所示的实验场景中得到了5台机器人的最终位置分布，可以看出机器人基本到达最终目标位置。粗略对比两幅结果图，仿真和实验最终的机器人位置分布情况基本相同。

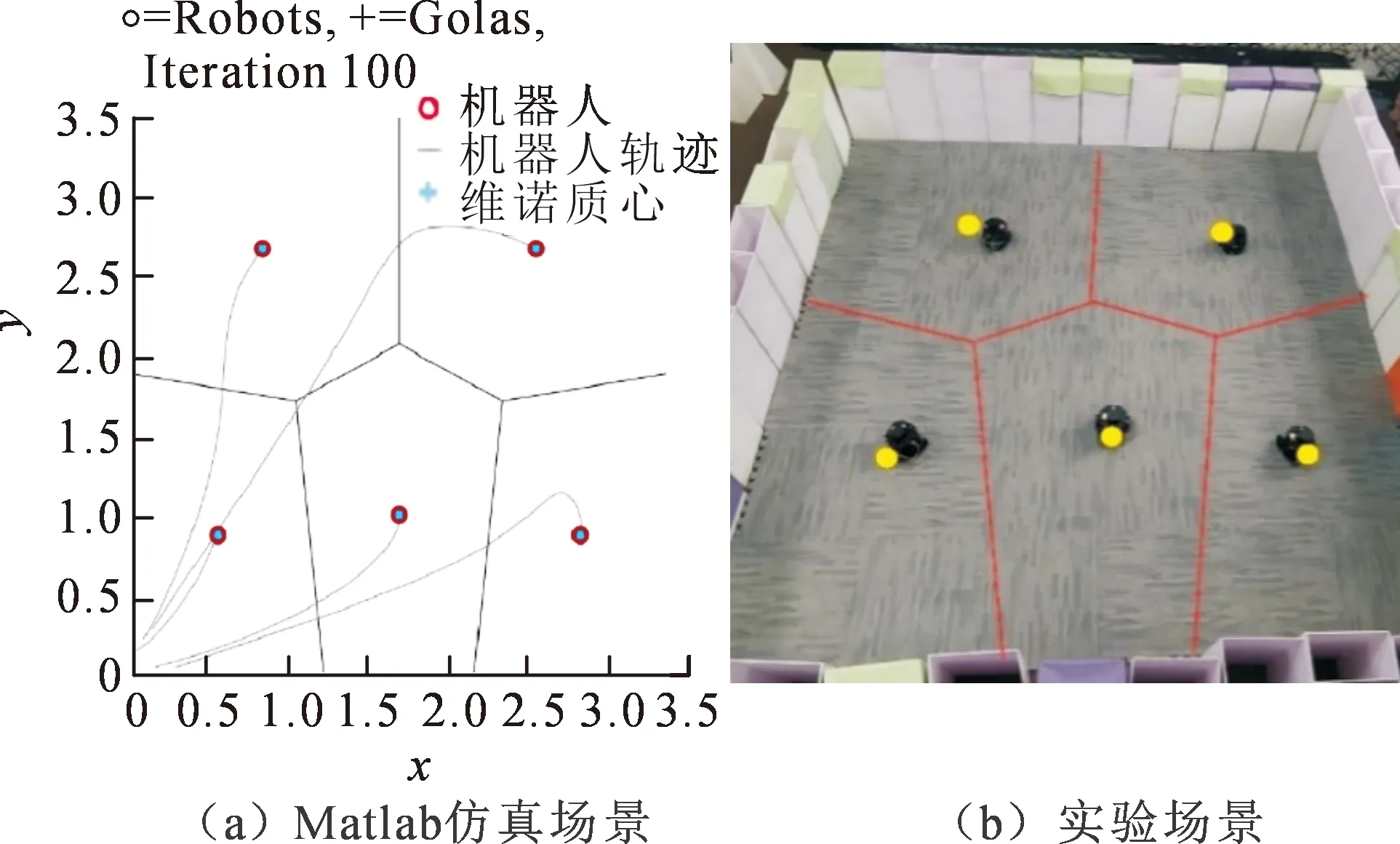
图20 迭代100次时集群机器人分布

图20(b)中从左上角开始，顺时针为机器人1、机器人2、机器人3、机器人4和机器人5，为了验证实验场景中机器人是否达准确到达了目标位置，表5中统计出了5台机器人在实验中的目标位置以及实验场景中实际到达的位置，并计算了目标位置和实际位置的误差。误差越大表示该机器人与目标位置的距离越远。

由于实际环境中机器人需要考虑到大小、地面摩擦以及通讯延迟等因素，故实验场景中的机器人并没有完全准确的达到目标位置，但从表5中可以看到，误差值都在合理范围内。根据实验可得，当算法趋于稳定后，实验场景中每个机器人都基本到达了场景的目标位置。

表5 凸环境下机器人位置误差

4.3 非凸环境下机器人实验结果与分析

如图21(a)所示，仿真场景为3.5 m*3.5 m的正方形，环境中间黑色部分为一个直径为0.7m障碍物，为非凸型区域场景。在左下角随机生成5生成点作为维诺划分的初始位置。图21(b)为对应的实验场景，为3.5 m*3.5 m的正方形中间放置一个蓝色圆柱形障碍物，其直径为0.7 m。在实验场景的左下方放置了5台Turtlebot3机器人，作为机器人初始位置。

图21 集群机器人初始位置

当仿真迭代32次时，达到如图22(a)所示位置，在前文提出的基于二次约束下的质心维诺划分算法的基础下，并没有将维诺细胞的质心位置计算至障碍物内，保证了每个机器人不会碰撞到环境中的圆形障碍物。机器人在运动过程中，利用模型预测控制得到可行轨迹。从图22(b)的实验场景中可以看出，实验场景中机器人的运动过程和达到的位置与仿真中基本一致。

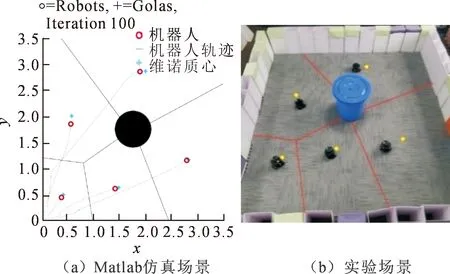
图22 集群机器人运动过程

由于环境密度函数为常数，机器人集群在场景中趋于均匀分布，平分任务场景区域。根据图23(a)的仿真实验，5台机器人最终收敛后到达目标位置，机器人基本上均匀地分布在场景中，对应的维诺细胞平分了整个任务区域，并且仿真中，机器人的运动轨迹也都避开了障碍物，实现了对非凸任务场景的合理划分。实验场景23(b)中，5台机器人均匀分布在场景内部，和实验中机器人最终到达的目标位置基本一致。

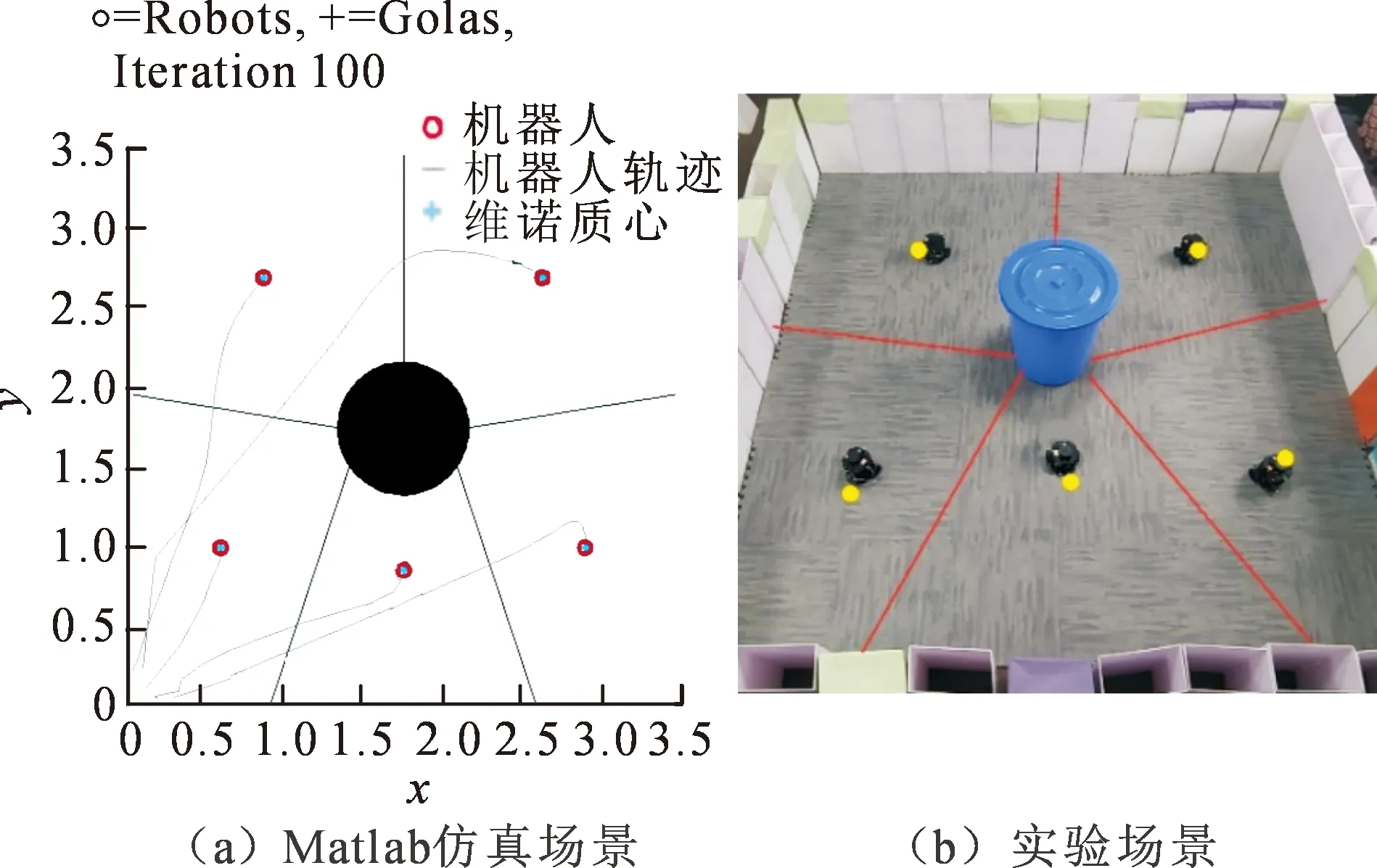
图23 集群机器人分布图

从左上角开始，顺时针为机器人1、机器人2、机器人3、机器人4和机器人5，为了验证机器人最终是否到达目标位置，表6中统计出了5台机器人在实验中的目标位置以及实验场景中实际到达的位置，并计算了目标位置和实际位置的误差，表6中位置误差都在合理范围内。结果表明，当算法趋于稳定后，实验场景中每个机器人都基本达到了场景的最优位置。

表6 非凸环境下机器人位置误差

实验过程中，通过二次约束下的质心维诺划分算法对非凸环境区域进行划分，得到在非凸区域环境下的质心轨迹，结合模型预测控制保证了机器人在运动到过程的安全性；在实验场景中，机器人的运动过程和对应的仿真环境大致相同，最终都得到了场景中机器人的最终分布。表明了本文算法能够完成真实场景的集群任务，并安全准确地到达最终目标位置。

5 结 论

1) 针对CVT算法在凸环境应用中的局限性，通过二次约束的方法，对维诺细胞及质心位置分别进行约束，以得到符合环境的集群机器人最终分布。将改进的CVT算法得到的质心轨迹作为MPC的参考轨迹，生成符合机器人动力学约束的可行轨迹，保证了机器人安全可行的达到CVT收敛位置。

2) 通过不同非凸环境的质心维诺划分仿真，对二次约束的CVT算法进行验证表明算法的可行性；结合MPC算法进行仿真，表明该方法可以有效解决各类约束问题，充分验证了机器人在非凸环境中自主运行的安全性。在5台ROS机器人上进行了实验验证，文中算法可以保证机器人在不同环境下安全的达到最终目的，完成集群相应任务。

3) 在未来的工作中，应当考虑到机器人的健康退化，通过模型预测控制在保证机器人安全的同时保证机器人集群整体性能、寿命的延长，设计一种可以平衡机器人集群系统性能，使机器人集群寿命达到最大化的方法的同时，也是保证机器人集群完成任务的坚实基础。