小学数学课堂中如何设计“好问题”

王荣森

一部好的电视剧要有好的剧本，一节高效的数学课要有好的数学问题。明代学者陈献章说：“学贵有疑，小疑则小进，大疑则大进。”美国数学家哈尔莫斯说：“问题是数学的心脏。”数学课堂上，教师提出的“好问题”，能引起学生的共鸣，激发学生的思考。师生互动的程度会直接影响到课堂效果，而只有在“好问题”的引导下，师生才能真正互动起来。那么，什么样的数学问题才算是“好问题”呢？“好问题”要能贴近学生的实际生活，揭示当堂课中知识的重难点;“好问题”要有数学价值和趣味性，既能解决生活中的实际问题，又能拨动学生的思维之弦;“好问题”要能激起学生思维的“火花”，成为学生主动探索数学的动力。

然而，在实际的课堂教学中，教师很多时候不注重提出“好问题”，导致师生互动的效果往往不尽如人意。究其原因，一是因为教师提出的数学问题流于形式，问题过小、过浅、重复的旧知过多，没有让学生进行数学思考的价值;二是因为教师提出的数学问题偏离学生生活实际，呈现出偏、难、怪等现象，不能将静态的数学知识转化为动态的生活情境，导致学生缺乏知识运用的灵活性、综合性、创造性;三是因为教师提出的数学问题不注重课堂中生成资源的利用，问题不能有效促进学生数学发展水平的提升;四是因为教师提出的数学问题不能恰到好处地揭示教学中的核心知识点。为了避免上述“真说话，假互动”的现象，教学中要设计师生互动的“好问题”。

一、设计贴近生活实际，体现实效性的“好问题”

生活中处处有数学。数学来源于人们的生活同时也服务于人们的生活。好的数学问题应能解决生活中的实际问题，充分发挥数学的应用功能。教师设计“好问题”，要体现数学知识的实效性，让学生亲身体验到学习数学的目的之一是解决我们日常生活中的问题，让学生感到学数学有用，从而使他们喜欢数学、自觉思考数学、主动学好数学。

如教学“整数加减法的笔算”一课时，教师可结合如下生活实际，设计数学问题。

今天，我女儿在网上买了一个地球仪，价钱是120元，快递费用是15元。昨天，我的手机收到一条短信提示，说我的手机本月已欠费20元，为了不影响正常通话，让我尽快缴费，我马上用手机交了200元话费。早上，我在上班的路上正好遇到一家外贸商店进行清理库存打折优惠活动，店内所有商品一律打折处理，我挑选了一个背包，优惠后的价钱是100元，优惠了30元。请大家动脑想一想、动口说一说，小组内同学相互交流一下，在老师这段文字叙述中，谁能根据这些信息提出一些有思考价值的数学问题？请用你们发现的数学信息结合数学知识来解决这些问题。在我们的日常生活中，也有这样类似的数学问题吗？请在小组内互相提出问题并用我们所学的数学知识加以解决。

教师利用自己亲身经历的真实生活事例，让学生认真阅读并从中发现有用的数学信息，与小组内同学交流、分享、总结，提出新问题。这样，不仅培养了学生的阅读能力，同时也增强了学生灵活运用数学知识解决问题的能力。在解决上述数学问题时，学生跃跃欲试，积极参与研讨交流。这样，通过“好问题”，教师把课堂交给了学生，使学生成为了学习的主人。

再如，在教学“可能性”一课时，我设计了这样的数学问题。

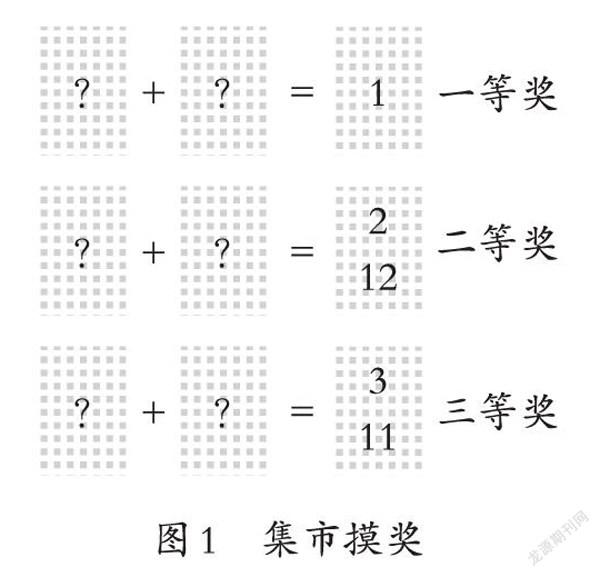
老师听说农村大集特别热闹，卖什么的都有，于是我利用上周日休息时间，起早去赶农村的大集。在大集上，有一些人正在开展摸奖赠礼品活动。摸奖规则是：有12张扑克牌，牌上的数字分别为1～6，每个数字的牌有2张。摸奖时，每次付1元钱，同时摸2张牌。2张牌上的数字之和等于1是一等奖，奖品是价值150元的家用菜刀一套;2张牌上的数字之和等于2和12是二等奖，奖品是价值5元的水果刀一把;2张牌上的数字之和等于3和11是三等奖，奖品是价值1元的筷子一双。我就想要这套家用菜刀，看到这个摸奖活动就动心了，结果摸了一次没有摸到，第二次也没有摸到，第三次还没有摸到，你们说这是怎么回事？但我很想摸到家用菜刀，你们想一想怎么改一下得奖条件，我摸到菜刀的可能性更大？（如图1）

经过思考学生发现，一等奖是不可能摸到的，因为2张牌上最小数字的和是1+1=2;摸到二等奖的可能性也很小，因为只有1+1=2，6+6=12两种情况;摸到三等奖的可能性也不大，但如果改成和为7，摸到的可能性就很大。教师以“集市摸奖”的题材作为数学问题，既贴近生活又解决了生活中的实际问题，让学生帮助教师利用可能性的原理来分析和判断，不仅帮助学生养成了运用数据进行分析推理的思考方式，而且也能使学生的创造性思维得到不同程度的提高。

二、设计揭示教学重难点，具有针对性的“好问题”

好的数学问题针对性要强，要能揭示知识的重难点，紧扣教学目标。教师要在知识的易错处提出数学问题，以达到突出教学重点、分解教学难点的目的，帮助学生扫清学习障碍。教师还应在学生思维的障碍处提出问题，这样有利于学生的知识迁移、知识建模，加深学生对所学新知的理解。

如在教学“异分母分数加减法”一课时，教师可提出这样的问题。

计算异分母分数相加减时，为什么不能直接把分子和分母相加减呢？

教师先呈现[1/2]+[1/3]= ？和[1/2][-1/3]= ？这两个数学问题，让学生利用通分的知识把这两个分数的分母都转化成分母是6的同分母分数后，再进行相加减，计算结果分别是[5/6]和[1/6];然后，教师可继续提问：异分母分数为什么不能直接相加减呢？在学生回答因为“分母不同”之后，教师追问：分母不同意味着什么呢？学生认为，分数单位不同，分数单位不统一不能直接相加减。这时，教师要再次追问：[1/2]+[1/3]还等于[2/5]吗？为什么不能直接相加呢？这样设计的数学问题针对性较强，在知识的关键处能引起学生的思考，使他们真正懂得其中的算理。這样通过问题引导的方式不同于“教师讲、学生练、教师反复强调”的方式，有效突破了本课知识的重难点，让学生明晰了“在计算异分母分数相加减时，不能直接把分母和分子进行相加减”的原因。

再如，在教学“圆的面积”一课时，教师先让学生动手操作，分别把圆平均分成8份、16份，然后将分开的部分拼组成一个近似的长方形。最后，教师让学生仔细观察这个近似的长方形并提出如下的数学问题：这个拼组后的近似长方形面积与原来圆的面积有什么关系？拼组后近似长方形的长、宽与原来圆的周长、半径之间分别有什么关系？这两个问题不但针对性强，而且还能揭示“利用长方形的面积公式推导出圆的面积公式”这个本课的重难点。为了使学生对数学知识掌握得更加准确，使数学知识更有说服力，教师可再次提出问题：若把这个圆平均分成32份、64份……，平均分的份数越多，拼组成的图形就越接近什么样的图形？这个长方形的长和宽就是原来圆的什么？怎么通过长方形面积公式（长方形面积=长×宽）推导出圆的面积公式？（圆的面积=[1/2]圆周长×半径=[1/2]×2πr×r=πr²）

学生在师生互动中体会到，把圆平均分的份数越多，拼成的图形就越接近长方形。这些“好问题”可以促使学生在课堂中积极思考，促使师生积极互动、探究，还可以使学生通过自己的思考学会新知识、感受转化的数学思想。

三、设计激发学生学习动力，具有趣味性的“好问题”

數学课堂中，“好问题”的呈现应具有趣味性和挑战性，要变枯燥的数学为有趣味的数学，使学生乐于接受。如果教师设计的数学问题趣味性很浓，符合学生学习的“口味”，学生表现出来的求知欲就强，就能促使学生主动、积极思考。在“好问题”的引导下，学生还可能会发现更多有价值的新问题。

如在教学长度单位、重量单位、时间单位及元、角、分等内容时，教师可设计这样的数学问题：

在括号里填上什么单位名称，可使算式1（ ）-1（ ）=9（ ）成立？

学生刚看到这样的问题时，先觉得是不可能的，同时也对究竟怎么填产生了探究的兴趣。在师生互动交流探究中，教师结合学生生活中的经验，引入解决问题的趣味情境，学生根据所学内容，结合具体的情境，不但填出了长度单位，而且还填出了元、角、分等单位。他们发现，这样的问题可以延伸出很多种答案，而且这些答案都是存在一定规律的。然后，学生还能自己总结出：只要是十进制单位都可以填。在此基础上，学生还能自己设计这类问题，如在括号里填出适当的单位名称，使算式1（ ）-1（ ）=23（ ），3（ ）+4（ ）=1（ ），1（ ）-10（ ）=50（ ），1（ ）-1（ ）=11（ ）成立。

这类数学问题的设计，不仅把数学中枯燥的“长度单位”等概念教学转化为学生学得津津有味的趣味数学，同时也激发了学生学习的动力。

“好问题”在有趣味性的同时，还应具有一定的思考价值，要能促进学生积极思考。喜欢挑战是学生的天性，具有挑战性的、探索性的数学问题能吸引学生主动去思考。

如在教学“分数的基本性质”一课时，教师可设计一个既有趣味性又有思考价值的数学问题：

暑假里的一天，爷爷买了一个大西瓜，先平均分成两半，然后把分开的一半西瓜平均分成6块，把其中的1块给了小明;妹妹小丽撒娇地抱着爷爷，想多要1块。于是，爷爷把另一半西瓜平均分成12块，拿出2块给小丽。想一想，小明和小丽谁分到得多？你认为爷爷这样分西瓜公平吗？（如图2）

这样的问题具有趣味性、挑战性，也具有一定的思考价值，能促使学生用数形结合的思想探索分数的基本性质。

总之，教师在课堂上提出“好问题”，是一种艺术，也是一门学问。“好问题”要能激发学生的内驱力，要能唤醒学生对知识的渴望和对学习的兴趣，使学生产生对未知的探索需求。这样，才能发展学生的数学思维，提高数学教学质量，让课堂真正成为学生学习的乐园。

（责任编辑：杨强）