基于细观孔隙结构的排水沥青混合料劈裂损伤分析
2022-06-28郭志栋李得健陈维斌杨鹏程
郭志栋,李得健,陈维斌,杨鹏程
(兰州交通大学 土木工程学院,甘肃 兰州 730070)
沥青混合料是由集料、沥青砂浆和孔隙共同组成的三相复合材料,孔隙结构对沥青混合料的力学性能和损伤特性有着极其重要的影响[1]。为了优化排水沥青路面设计并且延长路面使用寿命,有必要对大孔隙沥青混合料的开裂损伤机制进行深入了解和学习。近年来,沥青混合料的断裂特性在试验方法和数值模拟上已经有了广泛的研究,其中最具代表性的有美国战略公路研究计划(SHRP)确定的以间接拉伸试验(IDT)为主的沥青混合料低温性能的试验方法[2]。然而,试验大多都基于沥青混合料的宏观开裂特征,较大程度忽视了细微观尺度下的材料内部结构的变化。
随着计算机技术的发展,数值模拟的方法已经越来越受到研究者的欢迎,与实验室试验相比,数值模拟有着成本低、方便快捷的特点,但是由于计算技术的局限,以前沥青混合料的数值模拟大多基于混合料是均质材料的假设下进行的,这使得数值模拟结果与实际试验结果有较大的误差。CT扫描技术在沥青混合料设计中的应用使得这一问题得到很好的解决,CT 扫描和数字图像处理技术可以在不破坏沥青混合料组成结构的前提下快速准确地获取其细观结构信息,结合有限元技术便可对其内部结构进行细观重构和虚拟仿真[1]。
为了模拟损伤和断裂行为,内聚力模型(CZM)由于其在模拟裂纹产生和扩展方面的简便性和高效性,近年来越来越受到人们的关注。Barenblatt[2]在20世纪60年代早期首次提出该方法,并利用该方法研究理想脆性材料的断裂行为。Needleman[3]在20世纪90年代进一步发展了CZM技术,通过在具有指数内聚定律的有限元网格中引入内聚力单元来实现材料的损伤。该方法在沥青路面材料断裂力学领域的成功应用,对研究沥青混合料的开裂行为提供了极大的帮助。刘鹏飞等人[4]基于CT图像进行了间接拉伸试验,对不同压实条件制作的沥青混合料试件的界面断裂行为进行了研究。Souza 等[5]借助 CZM在细观尺度下对沥青混合料的Ⅰ型断裂模式进行了模拟。
尽管在CZM技术和微观结构表征方面取得了一些进展,但仍需要对沥青混合料复杂断裂行为的微观CZM模型进行进一步的研究。本文选取孔隙率分别为19.1%、20.2%以及22.7%的沥青混合料试件进行CT扫描,利用扫描的数字图像建立不同孔隙率的沥青混合料劈裂模型,并在沥青砂浆以及沥青砂浆-集料界面中插入具有双线性牵引分离定律的内聚力单元,对劈裂过程中不同孔隙率沥青混合料试件的应力分布以及开裂损伤进行研究。
1 材料与方法
1.1 配合比设计
为研究不同级配类型的排水沥青混合料内部空隙的分布特征,本文制备OGFC-13沥青混合料。由于OGFC混合料空隙率较大,粘附性低,因此选用橡胶沥青作为胶结料,调配3种不同级配,分别为OGFC-1、OGFC-2、OGFC-3,对应的沥青用量分别为4.70%、4.80%、4.90%。级配曲线如图1所示。
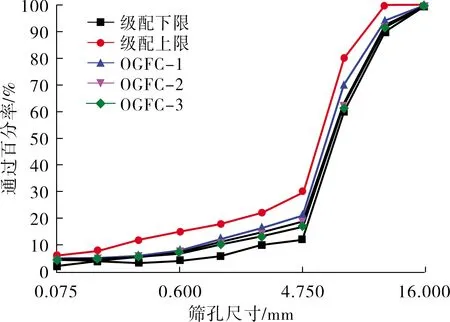
图1 级配曲线
1.2 内聚力本构模型
内聚力模型(cohesive zone model,CZM)是基于断裂力学理论在损伤力学框架中发展出来的一种模拟粘结面逐步分离的力学计算方法[6-8]。在混凝土、陶瓷等材料的开裂模拟中已经有了广泛的应用。CZM 的本构关系由内聚力区域单元的牵引-分离定律(traction-separation law)所定义,该定律表述了界面上的黏聚力与单元厚度方向上2个面之间相对位移的关系,如图2所示[9]。CZM具有多项式、指数、线性和双线性等几种常见形式,根据已有研究,双线性 CZM模型更适合模拟沥青砂浆和沥青-集料界面的开裂行为[10]。
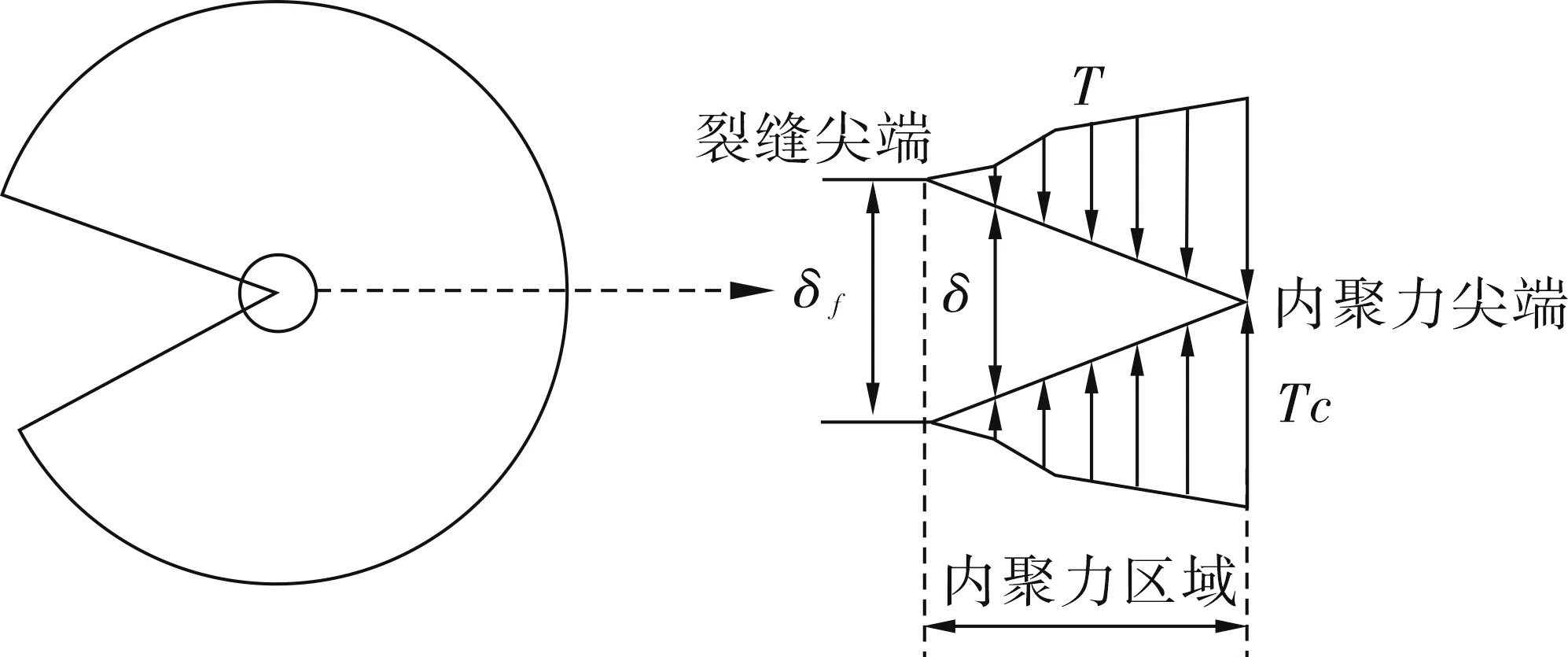
图2 裂纹扩展示意
双线性内聚力模型的T-δ曲线如图3所示,其中:T为内聚力;δ为裂纹面的相对位移;Tc为材料的力学强度,是内聚力所能到达的最大值,称为开裂强度;δ0为内聚力达到Tc时裂纹面的位移;δf为裂纹面的最大位移,称为失效位移;Gc为断裂能,是指裂纹面从位移为0直到完全分离所消耗的能量,也即材料从完好到断裂所吸收的能量。
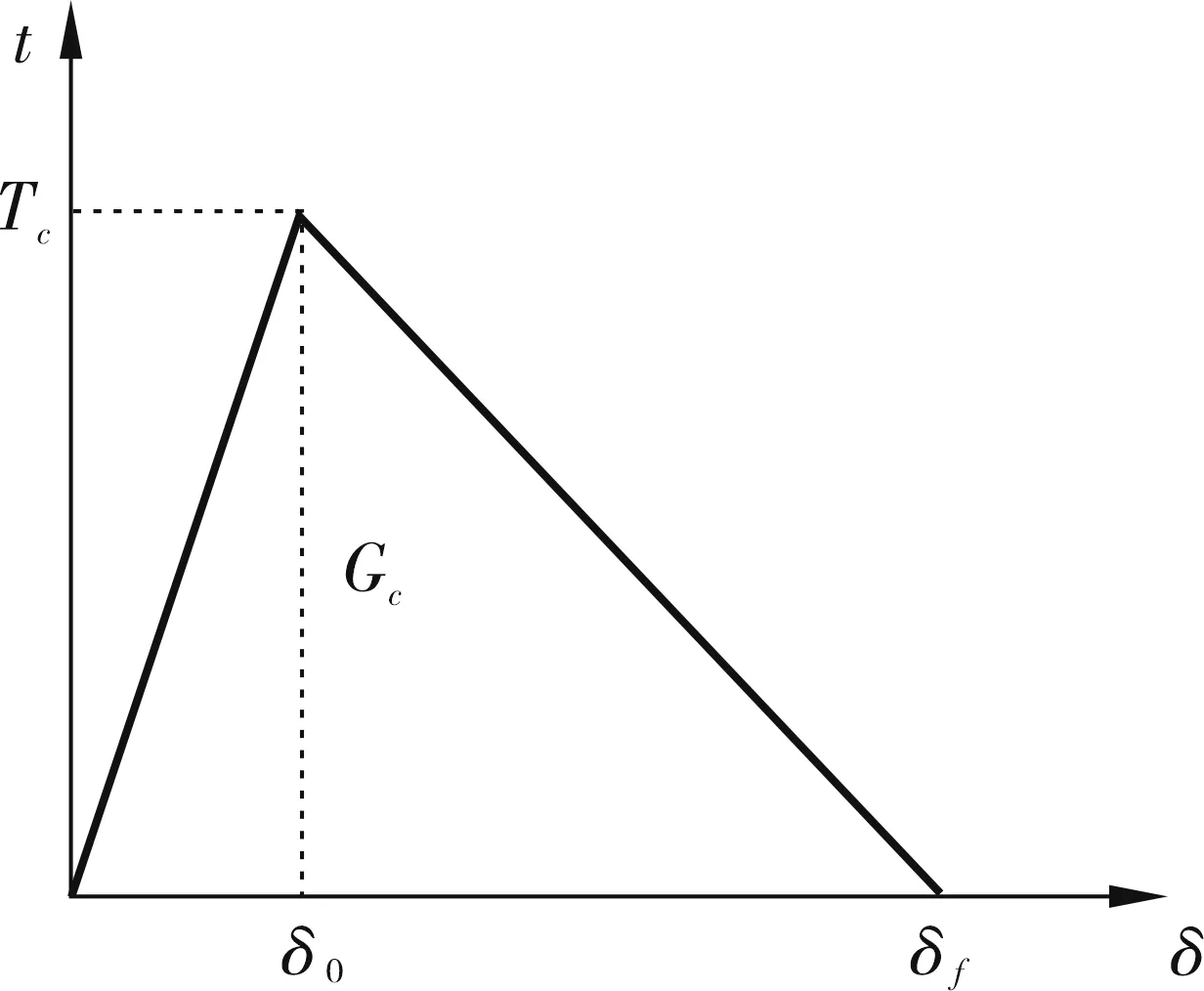
图3 双线性内聚力模型的T-δ曲线
双线性 CZM 模型可采用 ABAQUS 中的内聚力单元(cohesive element)实现,其主要参数断裂能Gc和抗拉强度Tc可通过试验获得。ABAQUS 中引入损伤系数D来表征材料的破坏水平,对于双线性CZM 模型中的D表达式见式(1)[9]。在裂缝的形成过程中,D从0随着荷载的施加增加到1。当D=0时,表示材料没有损伤,当D=1时,表示材料已经断裂。
(1)
式中:δmax为加载过程中裂缝面相对位移达到的最大值;δ0为内聚力达到抗裂强度时的位移值;δf为材料断裂时裂缝面的相对位移值。
1.3 CT扫描和数字图像处理
X-ray计算机断层扫描(CT)技术是一种无损检测技术,用于捕获材料内部的结构。X-ray CT 在扫描不同物质时,可以接收到不同的 X 射线衰减系数,将这些系数排列组成数字矩阵。再使用数字转换器,将数字矩阵中的每个数字都可以转换成具有不同灰度的小正方形,即像素(pixel),最后将像素按矩阵进行排列,就得到了CT 图像。
利用CT 扫描设备每隔 0.5 mm对沥青混合料试件进行等间距断层扫描,然后运用数字图像处理技术对扫描图像进行图像增强、图像分割与边缘检测,获取沥青混合料不同组成部分的二值化图像。将二值化图像矢量化处理并转化文件类型后,将其导入通用有限元软件 ABAQUS 中以建立沥青混合料二维细观虚拟试件,如图4所示。其中绿色部分表示沥青砂浆,黑色部分表示粗集料,空白部分表示孔隙。
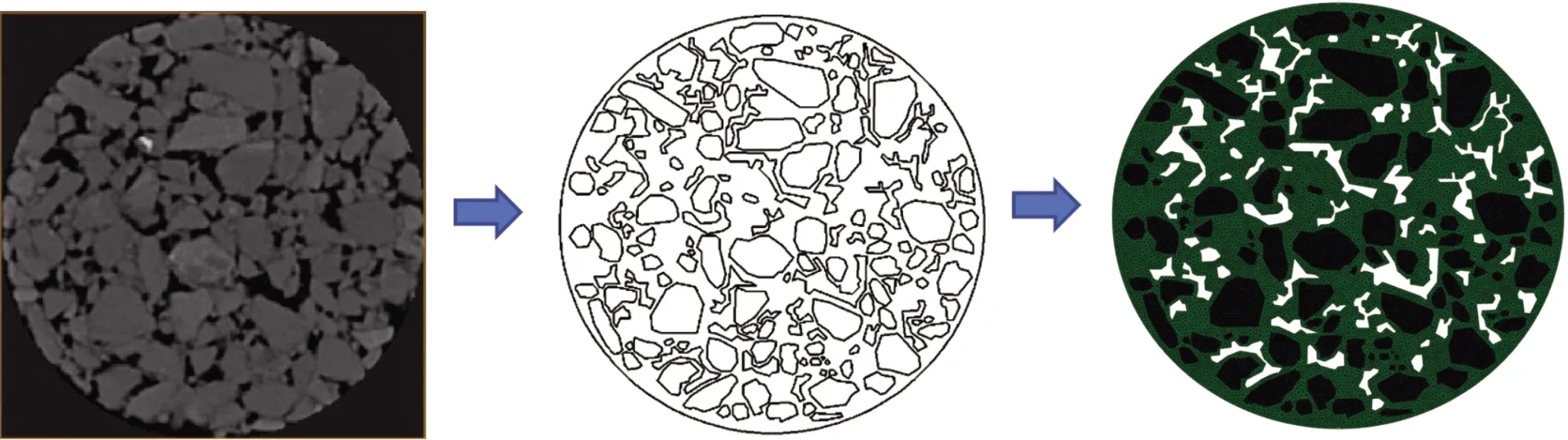
图4 CT图像转化为有限元模型
2 基于细观特征的有限元建模
2.1 材料参数
将粗集料定义为线弹性材料、沥青砂浆定义为粘弹性材料,根据OGFC沥青混合料15℃时的burgers粘弹性参数,并将其转换为ABAQUS中的prony级数,见表1。在进行有限元建模时,弹性模量和泊松比是粗骨料和沥青砂浆的2个弹性参数,而对于Cohesive单元,除了弹性模量外,还需要建立与材料损伤有关的参数。本文统一采用最大名义应力准则(Maxs)作为Cohesive单元损伤的起始准则,以断裂能和抗拉强度这2个参数来表征Cohesive单元失效删除的临界准则,具体参数见表2。

表1 OGFC沥青混合料黏弹性参数

表2 细观模型材料参数
2.2 有限元模型
利用 AutoCAD的sat接口,将矢量化后的信息导入ABAQUS有限元软件中,分别对集料和沥青砂浆构建有限元模型。参考沥青混合料试验规程,本模拟采用的劈裂条宽度为12.7 mm,模型直径为101.6 mm,厚度63.5 mm。有限元模型如图5所示,上端和下端的压条均设置为刚体,压条与沥青混合料之间为面面接触可以传递压力,模型两侧完全自由,上压条顶部施加垂直向下的荷载,加载速率为50 mm/min,约束横向位移和转角;下压条为全约束,即无法发生任何转动和位移。
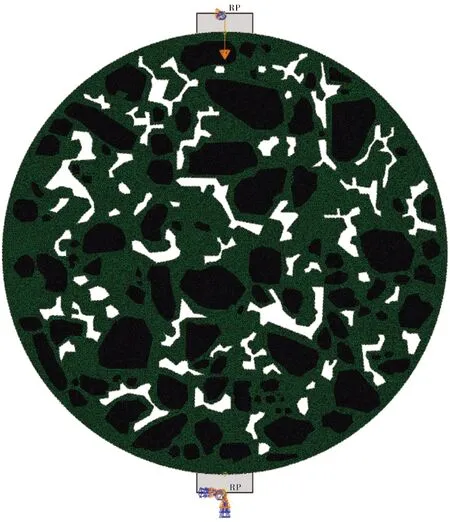
图5 劈裂试验有限元模型
在沥青混合料的细观结构中,潜在的裂缝路径可能穿过集料、沥青砂浆及沥青砂浆-集料界面。一般来说,由于粗集料的模量较高,粗集料比沥青砂浆更难破碎。因此,在本研究中假定开裂仅发生在沥青砂浆和集料-砂浆界面,插入的零厚度内聚力单元分为2组,分别为沥青胶浆和沥青胶浆-集料界面,在图6中用红色标出。

图6 试件中2种类型的内聚力单元
3 结果与分析
3.1 劈裂作用下沥青混合料应力分布
相同荷载施加及网格划分情况下的不同孔隙率沥青混合料的应力分布如图7所示,从图中可以看出,除在约束条件及荷载施加周围出现应力集中现象外,孔隙尖角附近的砂浆处也出现了较为清晰的应力集中,这导致在荷载施加过程中,孔隙尖端产生了较大的应力从而使沥青混合料的承载力大大降低。

图7 不同孔隙率沥青混合料试件劈裂模拟过程中应力云图
本研究选取不同孔隙率的沥青混合料试件沿直径X方向路径与Y方向路径的水平应力S11和竖向应力S22进行试件的内部应力分析,路径分布如图8所示。通过有限元模拟劈裂试验得到的S11和S22沿试件X方向和Y方向的分布规律分别如图9~10所示。从整体趋势上看,应力分布基本对称于试件中心,并呈现出多峰值的形状,而并非均匀的曲线,其原因有两点:一是由于试件的孔隙率较大,在孔隙周围会产生应力集中现象,使得孔隙尖端产生较大的应力;二是由沥青混合料的非均质性造成的,粗集料和沥青砂浆分别表现出不同的应力特征。
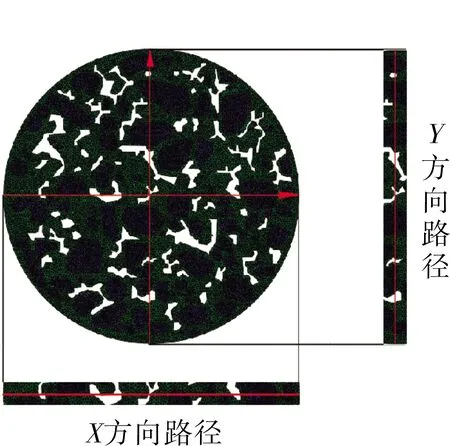
图8 路径分布
由图9可以看出,沥青混合料模型在X方向上的水平应力S11除部分位置发生突变外,绝大部分位置均为正值,并总体呈现出“两端小,中间大”的形状。这说明在X方向上试件受到的水平应力基本为拉应力(正值为拉应力,负值为压应力),且试件中心部位应力较大,两端应力较小。分析S11作为压应力出现的位置可以发现其均为空隙尖角附近的砂浆处。这是由于试件受到劈裂作用时,粗集料和沥青砂浆的存在会对空隙产生挤压作用,使得空隙产生较大压缩变形,从而对空隙附近的沥青砂浆产生水平压应力。而S22在X方向上的分布基本为负值,说明X方向试件受到的竖向应力为压应力,且中间应力较大,逐渐向两端递减,试件中心处应力最大。分析应力分布曲线上峰值的位置可以看出,最大压应力出现于粗集料集中的位置。这说明,当试件受到劈裂荷载作用时,沥青混合料试件中粗集料在X方向路径上承受较大竖向压应力,砂浆与界面承受较小的竖向压应力,该现象符合沥青混合料强度构成原理[11]。

(a)孔隙率19.1%
劈裂荷载作用下试件Y方向上的应力分布曲线如图10所示。水平应力S11在试件两端为负值,呈压应力;中间位置为正值,呈拉应力,且中间位置应力绝对值小于两端位置。而Y方向上的竖向应力S22基本均为负值,为压应力,且其绝对值同样呈“两端大,中间小”分布。同样,与X方向应力分布有一致的规律,S11压应力峰值分布在孔隙尖角附近的砂浆处,S22的压应力峰值出现在粗集料集中的区域。
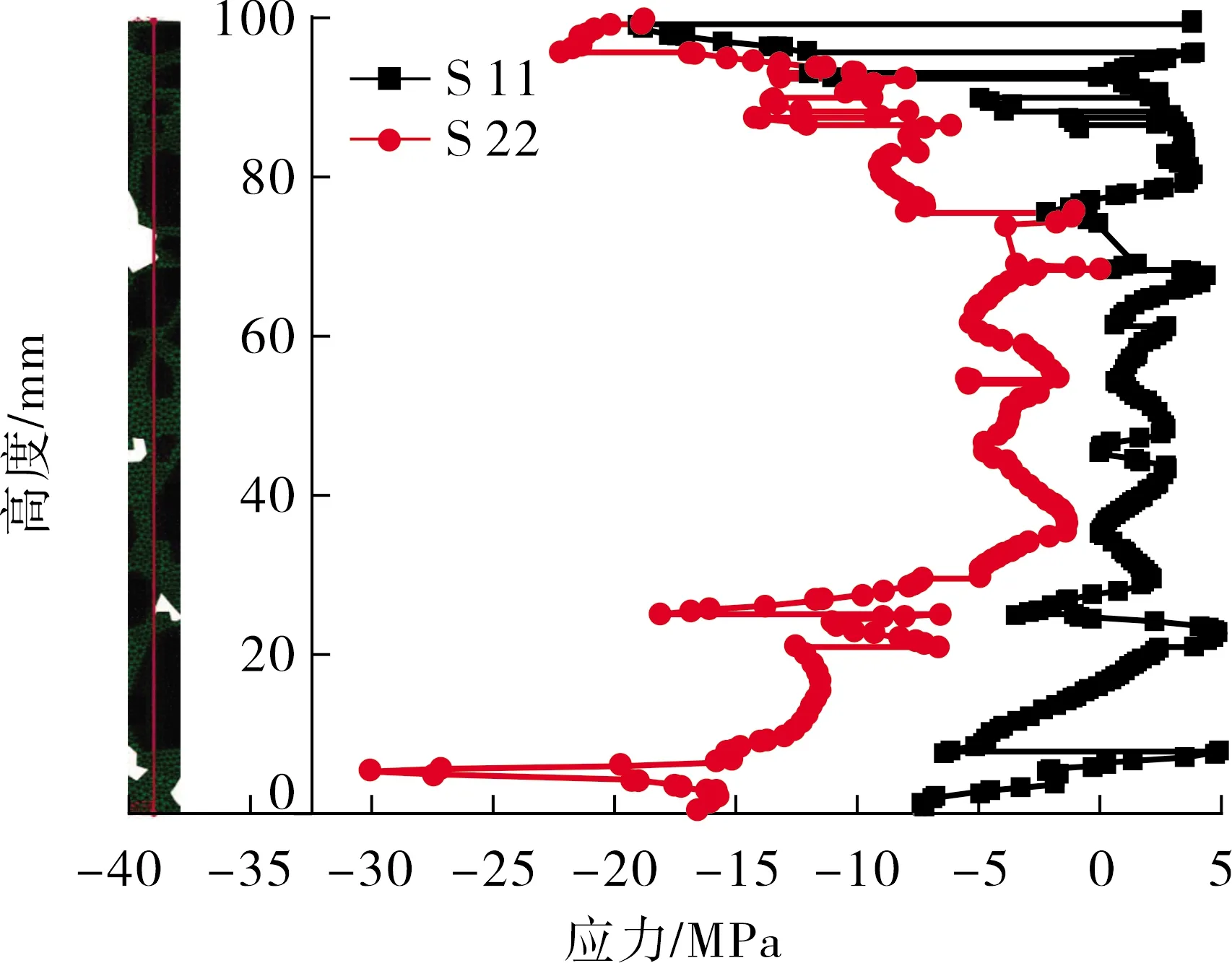
(a)孔隙率19.1%
综上所述,无论从试件X方向还是Y方向,水平拉应力基本为S11,而竖直应力 S22基本为压应力,这说明水平拉应力S11是沥青混合料产生开裂的主要原因。并且沿Y轴方向的拉应力普遍大于沿X轴方向拉应力,说明试件会首先沿竖直方向产生开裂。
同时,在图9~10中也可以清楚地看到:不同孔隙率对沥青混合料劈裂过程中的应力分布有着明显的影响;尤其对沥青混合料试件开裂影响最大的水平应力S11而言,无论是沿试件X方向还是沿试件Y方向,虽然部分位置的应力由于孔隙的存在和沥青混合料集料分布的不均匀性产生较大的突变,但是从总的趋势来看,随着孔隙率的增大,混合料内部的拉应力也随之增大,这使得孔隙率较大的试件在劈裂作用下更容易开裂[1]。
3.2 沥青混合料劈裂损伤分析
在劈裂模型中,当混合料试件内部的拉应力大于沥青砂浆和沥青砂浆-集料界面的内聚力单元的抗拉强度时,试件内部开始发生损伤,即产生裂缝,随着劈裂模拟中上压条位移的增大,沥青混合料试件裂缝逐渐扩展,直至试件完全破坏。选取孔隙率为20.2%的沥青混合料开裂过程(如图11所示),结合试件破坏过程中的荷载-位移曲线对大孔隙沥青混合料的劈裂损伤进行研究。

(a)抗开裂阶段
不同孔隙率沥青混合料试件在劈裂模拟过程中的荷载-位移曲线如图12所示,参照该曲线,沥青混合料试件在劈裂过程中分为3个阶段,分别为[12]:
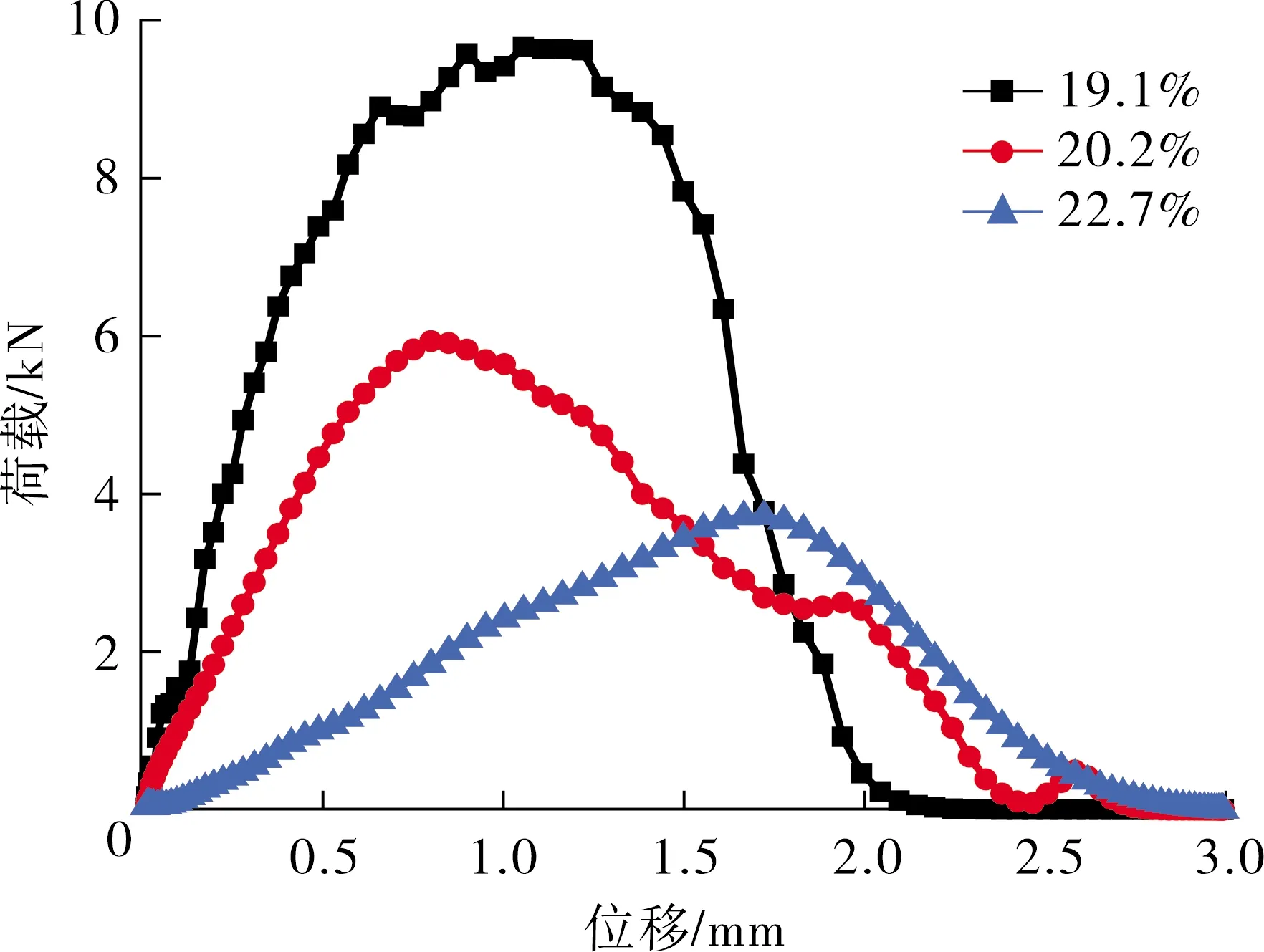
图12 荷载-位移曲线
1)荷载-位移曲线上升段。荷载峰值前半段为沥青混合料抵抗开裂的阶段,施加的荷载从0逐渐增大,但试件并未产生裂缝,此阶段对应图11(a)。
2)荷载达到峰值。荷载达到峰值代表沥青混合料试件中的沥青砂浆和孔隙不能抵抗荷载作用,开始产生微裂缝,此阶段对应图11(b)。
3)荷载-位移曲线下降段。荷载峰值后半段表示沥青混合料裂缝发展的过程,此时沥青混合料强度下降,试件中的裂缝开始发展延伸,裂缝逐渐变长变宽,当荷载接近0时,裂缝彻底贯穿整个试件,试件完全破坏,如图11(c)所示。
由图12可以看到,沥青混合料的孔隙率对劈裂过程中的荷载-位移曲线有很大的影响,随着孔隙率的增大,荷载-位移曲线的荷载峰值明显降低。这说明沥青混合料孔隙率越大,抵抗开裂的能力越差,这是因为孔隙率越大,沥青混合料试件裂缝扩展过程中更易找孔隙与沥青砂浆交界处的薄弱部位,使开裂更加顺畅,从而降低其抗开裂性能。
图13~14分别显示了不同孔隙率的沥青混合料的劈裂抗拉强度和开裂过程中所需的能量,可以看出,随着孔隙率的增大,沥青混合料的劈裂抗拉强度降低,开裂所消耗的能量也明显降低。这与之前学者的研究有较好的一致性[13],这也说明了本研究中基于沥青混合料细观特征的劈裂模拟的可靠性。
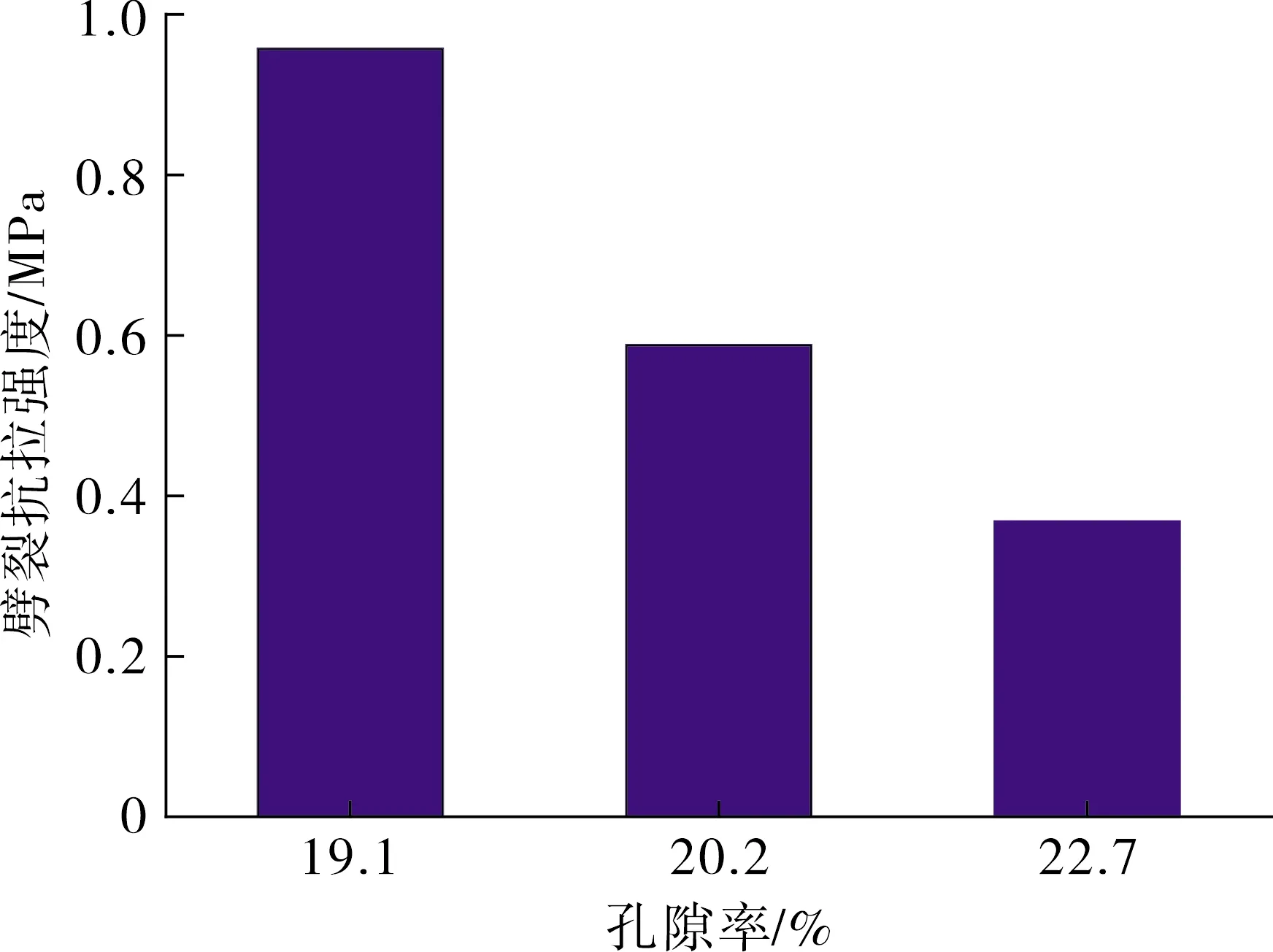
图13 劈裂抗拉强度
4 结论
1)通过分析沥青混合料试件在X方向以及Y方向的应力分布可以看出,孔隙的存在以及粗集料的分布对混合料应力分布有很大的影响,往往在孔隙尖端以及粗集料分布处应力会发生突变,使得应力分布以多峰值的状态呈现,并且随着孔隙率的增大,对沥青混合料开裂起决定作用的拉应力也随之增大。
2)结合试件破坏过程中的荷载-位移曲线以及试件在劈裂作用下的开裂特征,可以将试件劈裂过程分为3个阶段:① 荷载持续增大,试件处于抵抗开裂的阶段;② 荷载达到峰值,试件损伤开始;③ 荷载开始降低,试件裂缝扩展,直至完全破坏。
3)孔隙的存在对沥青混合料试件的开裂性能有很大影响,随着孔隙率的增大,试件破坏过程中的荷载峰值降低,劈裂抗拉强度也随之降低,开裂过程所需的能量也明显减少。
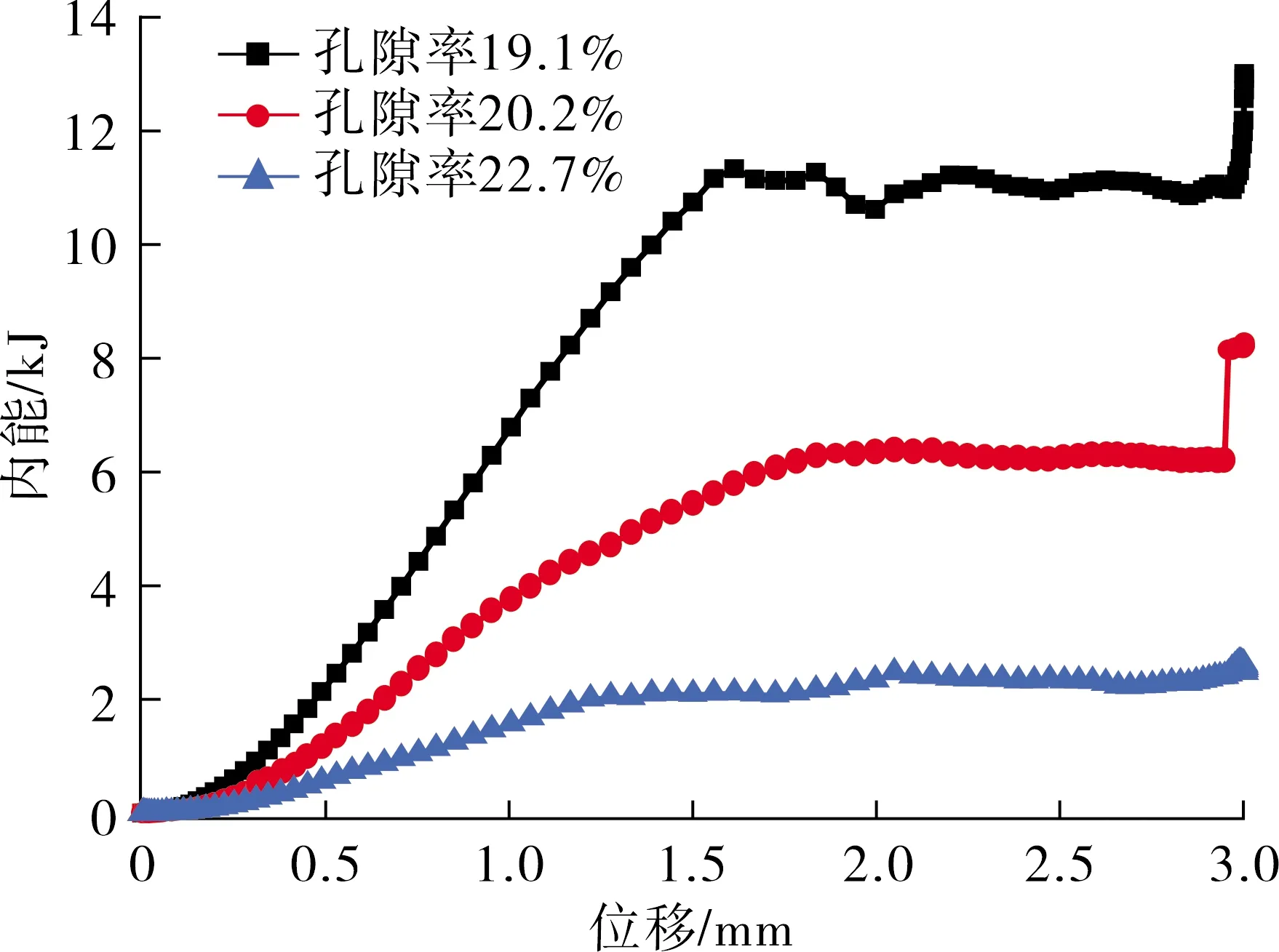
图14 内能-位移曲线
