仿象鼻子实验平台的设计与运动学仿真

杨 淼，狄杰建，赵玉侠，赵全亮

（北方工业大学机械与材料工程学院，北京100144）

1 引言

传统的刚性机械手臂和仿人手的机械装置已广泛应用于人类社会生产和生活中。传统刚性机器人在资源开发、排险救灾、社会服务和军事、航天等方面也得到广泛应用，发挥着巨大的作用。其广泛的应用得以使人类从繁重的劳动中解脱出来，同时也提高了生产效率。传统的机器人操纵臂是由刚性连杆通过刚性运动副连接构成的，但因其自身刚性结构限制，灵活性有限，无法适应客观多变的现实环境，这些缺点限制了其在复杂领域的应用，如核能危险处理、空间任务、救灾探测等[1-3]。随着社会发展，在诸多领域出现了各种特殊繁杂的工况情况，对传统的机械手臂提出了新的要求，包括安全的人机交互、安全的机器与环境之间的交互、自身的灵活性以及智能性。例如在狭窄灾害现场环境中，危险的核能检修作业中，以及在家无人照顾老年人的生活问题中均要求相应的操作手具有更高的顺应性、灵活性、智能性，更好的实现人机交互。仿象鼻机器人作为软体机器人的一个分支得到了持续广泛的关注和研究。仿象鼻机器人充分利用了现有特殊的柔性材料[4-5]，比如橡胶、SMA弹簧、聚合物等。所使用的柔性材料从材料性能上更加接近生物体本身，使仿象鼻子机器人具有智能性，从而获得像生物一样灵活，环境适应能力强的象鼻子，降低了控制的复杂度，实现高灵活性和良好交互性。

设计一种新型仿象鼻子机器人实验平台，整个实验平台结构设计紧凑简单，其结构很好的融合了常规的力、位移传感器，使整个机械臂实现半闭环控制。同时利用ADAMS 验证实验平台运动的可行性，并探究了实验平台在真实条件的运动状况。

2 结构设计

仿象鼻子实验平台的3D模型与实物，如图1所示。实验平台总体宽度678mm，高度为980mm。整个实验台由软体机械臂、滑轮组1、滑轮组2、支撑斜板、平台底座、步进电机、力传感器、位移传感器等部分组成。每节软体机械臂由三根呈120°均布的钢丝绳进行拉动。钢丝绳末端固接在电机绕线轮上，步进减速电机驱动电机绕线轮转动，从而拉动钢丝绳使机械臂弯曲。钢丝绳前端则通过螺栓形式固接在弹簧支撑盘上，然后通过滑轮组2将钢丝绳引入到位移传感器过渡板上，如图2（a）所示。位移传感器过渡板通过螺母固定在位移传感器上，随着位移传感器过渡板的移动进行相应的位移测量。钢丝绳通过滑轮组1最后固接在电机绕线轮上，力传感器通过螺栓形式与滑轮组1进行连接，以此来测试钢丝绳拉力，如图2（b）所示。

图1 平台3D模型与实物图Fig.1 Platform 3D Model and Physical Map

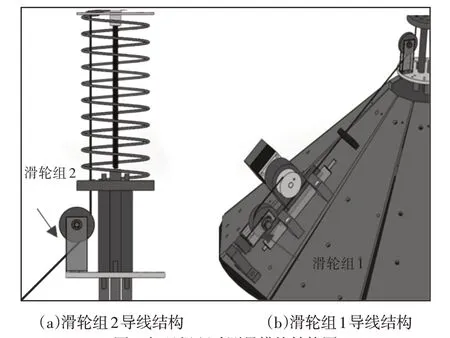
图2 钢丝绳驱动测量模块结构图Fig.2 Wire Rope Drive Measurement Module Structure Diagram

仿象鼻子实验平台的软体机械臂3D模型及实物，如图3所示。

图3 软体机械臂3D模型及实物Fig.3 3D Model of the Mechanical Arm and Its Physical Object

每节软体机械臂分别由一个圆柱螺旋弹簧和一个中心支撑弹簧构成。中心支撑弹簧通过弹簧支撑盘中心处的螺纹杆进行相应固定。在整个机械臂实现空间弯曲运动，软体单元应具有一定的弯曲刚度，选用中心支撑弹簧因其具备以下3个功能：

（1）因其支撑作用，使单节机械臂不可压缩；（2）其良好的弹性可满足机械臂连续弯曲运动的需求；（3）当机械臂的圆柱螺旋弹簧不受拉力时，其适当的刚度可以使弹簧恢复至初始的竖直位置。中心支撑弹簧材料为碳钢材料，具有高弹性，外径为8mm，线径为1.2mm，长度为130mm。

机械臂弯曲情况，如图4所示。电机需要根据力、位移传感器的数据来进行协调驱动，从而控制机械臂的空间位姿，以此来实现机械臂末端到达指定位置，同时利用高速摄像机对机械臂的空间位姿进行数据采集。

图4 实验照片及高速摄像仪Fig.4 Experimental Photos and High Speed Camera

3 运动学分析

仿象鼻子实验平台弯曲结构由四个关节段串联构成，为了便于说明机械臂整体运动控制问题，首先以单节为例进行分析，然后采用串联机器人运动学方法分析整个弯曲结构的运动。本文采用旋量法对单节运动学进行分析［6-7］。本节运动学分析基于以下前提条件：

（1）假定在弯曲过程中单节的曲率是瞬时均匀的，每节弯曲单元不可压缩和拉伸；（2）钢丝绳在弯曲过程中假定为等曲率的曲线。

3.1 单节驱动空间与关节空间的映射

在象鼻子连续体机器人单节运动过程中，通过3根呈120°的钢丝绳进行驱动，从而改变其弯曲角度θi-1和旋转角度ϕi-1。因此我们采用圆弧参数来描述单节位姿，其中描述三根钢丝绳实际长度。单节弯曲单元关节参数通过几何运算可求得，其结果为：

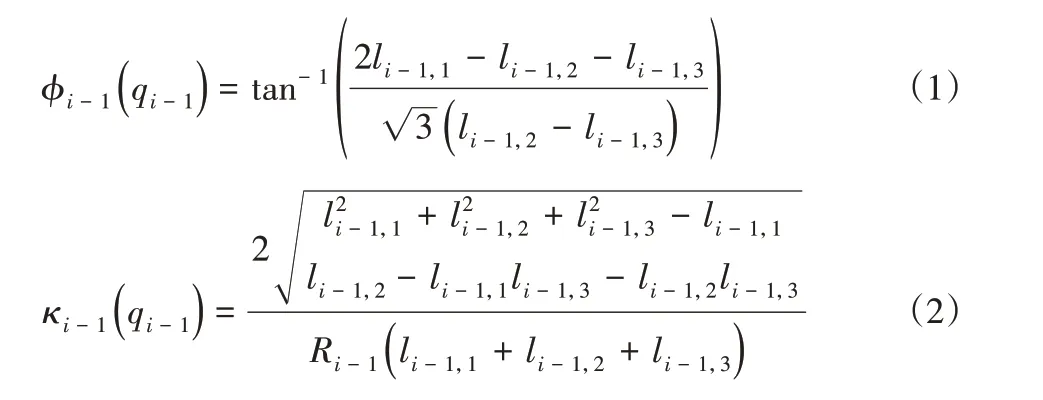
式中：ϕi-1—旋转角度；θi-1—弯曲角度;κi-1—机械臂οi-οi-1的曲率；li-1,1、li-1,2、li-1,3—各节机械臂内三根钢丝绳的长度；Ri-1—钢丝绳端距离弹簧支撑盘中心的距离。

通过几何运算来求解关节参数∅i-1,κi-1，从而确定从驱动空间到位形空间的正向运动学。

3.2 单节位形空间与操作空间的映射

实验平台有多段连续体组成，单段机械臂保持曲率恒定，其自身即不能压缩也不能拉伸。单段机械臂底部固接坐标系Oi-1-xi-1yi-1zi-1，端部固接坐标系Oi-xiyi zi，其中θ为单段机械臂底部与端部的夹角，ϕi-1为单段机械臂相对于中心轴的转角，单段机械臂位形空间由参数来定义，对于单段机械臂运动可以分为空间弯曲和绕中心轴转动，如图5所示。

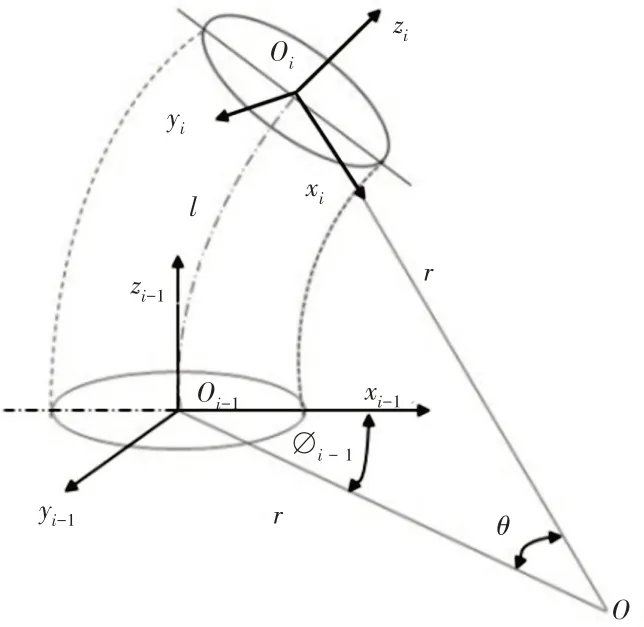
图5 单节位形空间参数Fig.5 Single Node Configuration Space Parameter

可引入如下扭曲坐标：

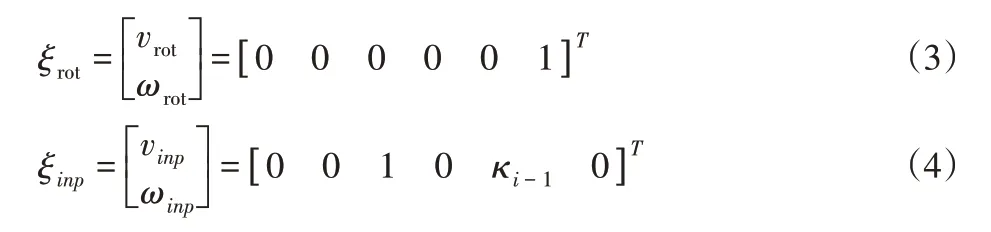
式中：v—相对于线性的运动；ω—相对于角度的运动。

然后利用楔形算子“＾”将矢量从三维空间映射到李群李代数，其运算结果如下：

根据式（7）和式（8）可获得从位形空间到操作空间的均匀变化矩阵，对于平台整个机械臂其相应的齐次变换矩阵如下：

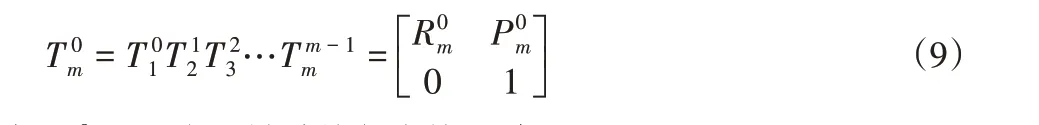
3.3 单节机械臂工作空间分析

机械臂的工作空间是连续体机器人性能的重要指标，弹簧弯曲使其自身的形状发生改变，从而改变其工作空间。单节机械臂具有2个自由度，它的工作空间由弹簧的固定参数以及弯曲角度θ和偏转角度ϕ来描述。单节机械臂的长度l为定值，单关节弯曲角度θ和偏转角度ϕ为变化值，其范围如下：

机械臂末端位置矢量式（8）和上述范围式（10）来确定仿象鼻子机器人单节机械臂末端端点的空间位置分布，使用Matlab绘制其工作空间，如图6所示。

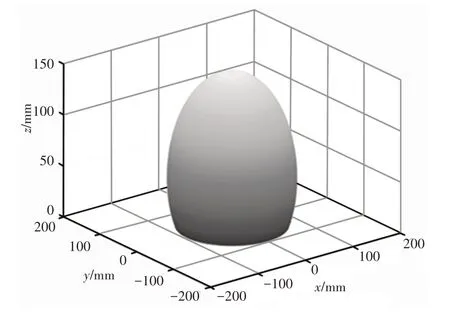
图6 单关节工作空间示图Fig.6 Single Joint Workspace Diagram

4 ADAMS单节机械臂仿真及结果分析

为了研究平台机械系统特性，利用虚拟样机分析软件ADAMS对连续体进行建模与仿真[8]。对实验平台机构进行相应简化，对其刚柔耦合系统进行研究。由于本实验平台由四节柔性机械臂组成，其结构相对复杂、自由度较多，所需仿真时间较长，文中着重介绍单节机械臂的刚柔耦合系统的建模与仿真，以此来验证平台的运动学规律。

4.1 单节机械臂建模

ADAMS柔性体建模方法有三种：（1）将连接件离散柔性化。将钢丝绳离散为多段刚性构件，离散构件之间独立存在，在其之间添加柔性连接来模拟钢丝绳。单节离散构件整体尺寸相对钢丝绳整体长度需足够小，这样来模拟钢丝绳。（2）利用ANSYS生成MNF文件导入ADAMS中。利用有限元软件将钢丝绳离散成细小的网格，并进行模态计算，将计算的模态保存为模态中性文件MNF。将其读取到ADAMS建立柔性体。该仿真精度高但仿真时间较长。（3）利用ADAMS里的Flex模块直接在ADAMS里建立柔性体MNF文件，利用其生成的柔性体来替代钢丝绳。

分析以上三种方法的优缺点，这里绳采用ADAMS里物体模块拉伸圆柱体来模拟钢丝绳，将钢丝绳离散若干节小圆柱体，小圆柱体之间采用轴套力来连接[9]。离散的小圆柱体之间的力学模型[10]，如图7所示。

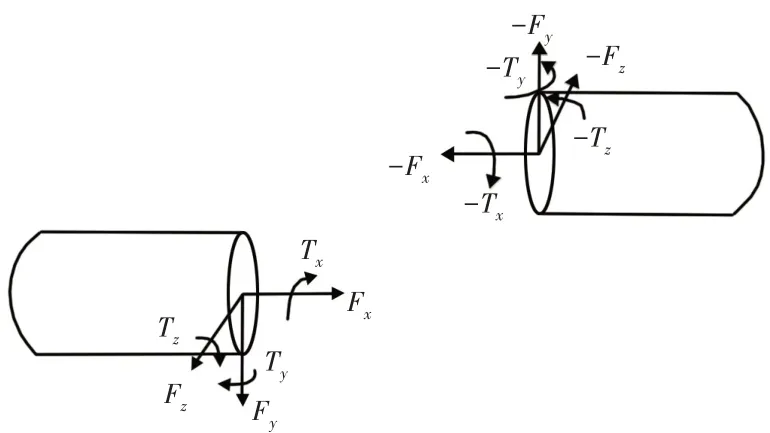
图7 离散圆柱体之间的力学模型Fig.7 Mechanical Model between Discrete Cylinders

轴套力实际上是由3 个力分量和3 个力矩分量构（FX FY FZ TX TY TZ），在2个离散的构件之间施加一个柔性力。在2个相互作用构件建立2个坐标标记点，轴套力的计算公式如下所示：

式中:F—轴套力；T—力矩；K—刚度系数；C—阻尼系数；R—2标记点之间的相对位移；θ—2标记点之间的转角；v—2标记点之间的相对速度；ω—2标记点之间的角速度。

4.2 单节机械臂约束及驱动

圆柱螺旋弹簧与中间支撑弹簧分别与上下弹簧支撑盘采用固定副进行相应连接。对于驱动单节机械臂里的三根钢丝绳，钢丝绳前端与上弹簧支撑盘采用固定副连接，钢丝绳末端与电机绕线轮采用固定副连接。电机绕线轮与两个滑轮分别与大地建立转动副。为提高计算效率，删除不必要的虚拟样机部件，只保留滑轮、钢丝绳、弹簧、弹簧支撑盘主要结构。简化后的虚拟样机模型，如图8所示。

图8 单节虚拟样机模型Fig.8 Single-Section Virtual Prototype Model

电机转动带动绕线轮转动，故在电机绕线轮加载设置好的三个驱动函数，通过函数控制机械臂的弯曲，所加载的三个驱动函数预计使单节弹簧向左弯曲。其中平面最左侧电机绕线轮加载驱动Motion_a，另外两电机绕线轮加载驱动函数，如表1所示。

表1 驱动及控制函数Tab.1 Drive and Control Functions

4.3 ADAMS仿真及结果分析

对搭建平台进行仿真模拟工作，并校核检查模型可行性。对单节机械臂进行控制仿真，仿真时间设定为0.2s，步数为2400。对模型进行仿真，确认如下内容：（1）单节机械臂末端的运动轨迹的正确性；（2）单节机械臂的运动轨迹与理论值的对比。在原设置的驱动函数条件下，0.2s后单节机械臂弯曲变形图，如图9所示。

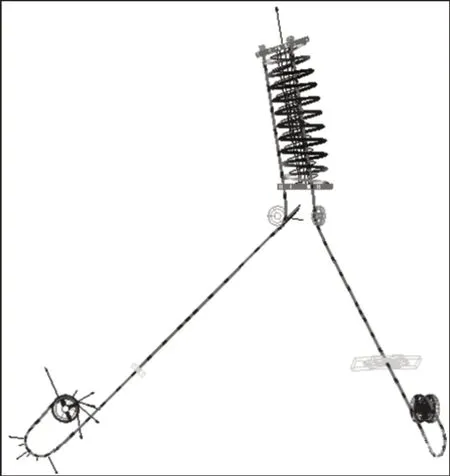
图9 单节机械臂的运动仿真Fig.9 Motion Simulation of a Single-Section Robot

4.3.1 单节机械臂钢丝绳拉力与末端位移的关系

蓝颜色曲线代表钢丝绳拉力随着弹簧的弯曲，钢丝绳拉紧其自身的拉力也随之增大，如图10所示。根据预先设置的驱动函数，可知机械臂整体向左弯曲。根据图10可知随着弯曲侧钢丝绳拉力逐渐增大，单节机械臂向左侧弯曲，单节机械臂末端主要在X、Z轴方向上发生位移，其在Y轴方向上基本未发生位移。当弯曲侧钢丝绳拉力达到最大时，单节机械臂末端在X、Z轴方向的位移量达到最大。

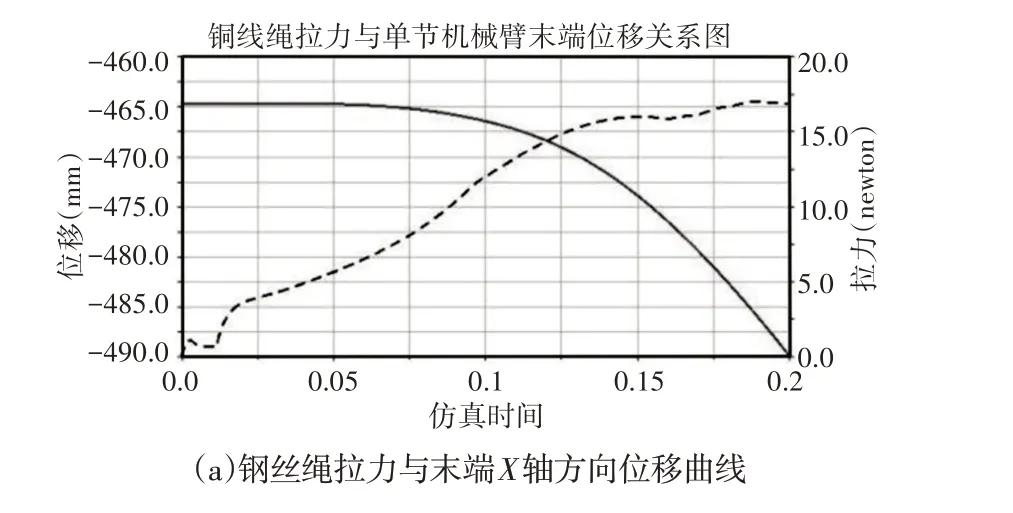
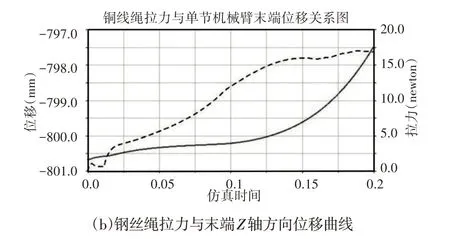
图10 钢丝绳拉力与末端位移关系图Fig.10 Wire Rope Tension and End Displacement Diagram

4.3.2 单节机械臂末端运动轨迹分析

单节机械臂末端中心X、Z位移初始值不是零是由Solidworks初始建立的三维模型坐标不是原点造成的，但是其不会对数据结果造成影响，如图11所示。

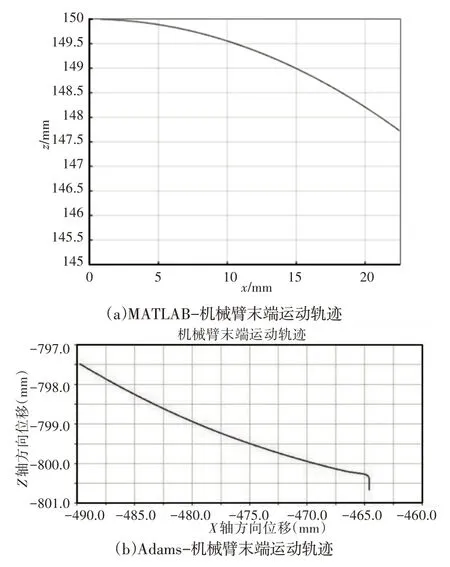
图11 AMTALB与ADAMS仿真轨迹图Fig.11 AMTALB and ADAMS Simulation Track Diagram

由于装配误差、材料易变形、弹簧支撑盘自身重量等因素的影响，使得单节机械臂在平面内弯曲X、Z轴方向位移与理论值存在误差。

根据图11的MATLAB 理论仿真可知当单节机械臂末端中心X轴方向位移量为25mm 时，Z轴方向位移量为2.8mm。根据图11的ADAMS仿真可知X1轴方向位移量为24.8mm，Z1轴方向位移量为，误差率为0.65%。

4.3.3 单节机械臂包角分析

单节机械臂仿真按照包角60°对三个电机分别进行相应的驱动设置，下弹簧支撑盘固定，代表X、Y、Z方向位移的红色虚线没有发生变化，如图12所示。

上弹簧支撑盘因弹簧弯曲，代表X、Y、Z方向位移的黑色点划线都发生相应变化，如图12所示。根据仿真结果计算得出包角为56.7°，误差率为5.5%。

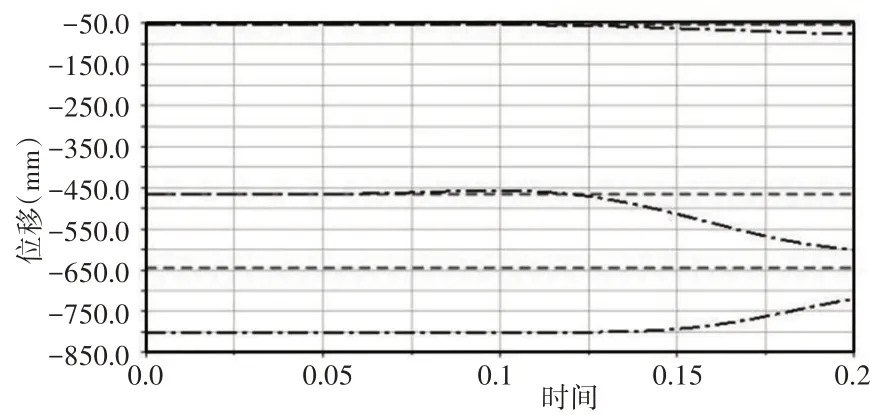
图12 单节机械臂上下弹簧支撑盘位置图Fig.12 Single-Section Mechanical Arm Upper and Lower Spring Support Plate Position Map

4.3.4 四节机械臂仿真算例

四节机械臂仿真按照包角120°对十二个电机分别进行相应的驱动设置。第一节机械臂下弹簧支撑盘固定，代表X、Y、Z方向位移的红色虚线没有发生变化，如图13所示。第四节机械臂上弹簧支撑盘因弹簧弯曲，代表X、Y、Z方向位移的黑色点划线都发生相应变化，如图13 所示。根据几何理论四节机械臂包角为120°时，第四节机械臂末端与第一节机械臂下弹簧支撑盘质心距离为R0，ADAMS仿真值为=119.6，误差率为24%。

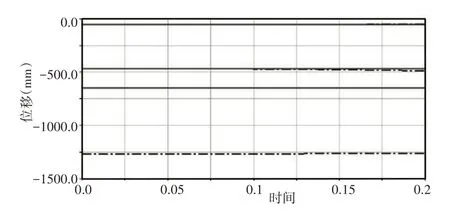
图13 四节机械臂上下弹簧支撑盘位置图Fig.13 Four-Section Mechanical Arm Upper and Lower Spring Support Plate Position Map

5 结论

通过分析大象鼻子生物特性和已有设计的大象鼻子连续体机器人的结构特性，设计了一种新型仿大象鼻子连续体机器人结构。用旋量法对仿大象鼻子连续体机器人的位姿及工作空间进行分析，同时利用ADAMS软件对较为复杂的刚柔耦合系统进行仿真。机械臂ADAMS的仿真结果验证了运动学分析的正确性，对平台结构设计的可行性、电机驱动关系、机械臂的空间位姿对比提供了数据支撑，并为平台后期实验起到一定的指导意义。