管材特性对黏稠油水环输送稳定性的影响分析

李 鹏，尹晓云，杨思远，胡 可，邓小娇，刘少钧，MASTOBAEV Boris N

（1.中国石化西北油田分公司 石油工程技术研究院，乌鲁木齐 830011；2.西南石油大学 石油与天然气工程学院，成都 610500；3.新疆油田分公司 吉庆油田作业区，新疆昌吉 831700；4.中国石油勘探开发研究院，北京 100083；5.中国石化川气东送天然气销售中心，武汉 430205；6.Department of Transport and Storage of Oil and Gas，Ufa State Petroleum Technological University，Russia Ufa 450062）

0 引言

随着轻质原油的不断开采，油田已进入重质原油开采阶段［1］。针对稠油黏度高、流动性差而不能直接管输的问题，目前多采用加热、稀释、乳化等降黏减阻方法，但这些传统的处理方法都不同程度地存在一些问题，如处理量大、能耗高、建设成本及运行费用高、油品品质变化大等。为此，学者们基于多相流型中中心环状流摩阻最低的观点［2］，提出利用外层低黏水环包裹核心高黏稠油的水环输送技术。该技术自诞生以来就备受关注，并因其独特的低能耗优势成为近年来黏稠油输送领域的新热点。

目前，国内外学者对水环输送稠油技术进行了较为广泛和深入的研究，主要采用理论分析、实验研究与数值模拟等手段，主要涉及水环发生器的研制与优化，油-水环状流的流型特征与压降特性，水环输送管道的停输再启动问题等方面［3-7］，少有针对水环输送稠油过程中其结构稳定性的探讨［8］。但要实现水环输送技术的工业化推广应用，首先必须解决水环边界层的稳定性问题，这样才能确保油-水环状流在长时间、长距离的现场管输中仍能保持相对稳定的流动状态。

本文采用数值模拟方法探究水平管中管材特性对油-水环状流结构稳定性的影响，通过对比分析不同工况下的油水两相体积分数分布特征、轴向速度分布特点、管道沿线压力变化特性等综合评价水环稳定性的强弱，为通过管材表面改性处理方法增强油-水环状流的稳定性提供理论参考。

1 模型建立与验证

1.1 控制方程

由于所涉及的流体介质稠油和水是2种互不相容的液体，所关注的环状流在管道中形成稳定流动形态后存在明显的交界面，因此选用VOF模型开展稠油-水环三维管流的数值模拟研究，其基本方程如下［9］：

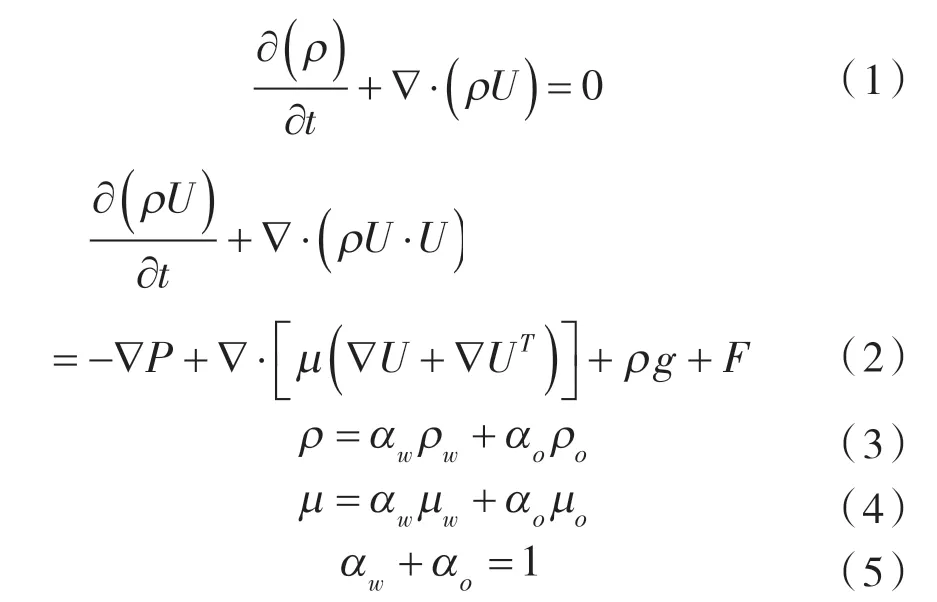
式中 ρ，ρo，ρw——流体、油相、水相密度，kg/m3；

μ，μo，μw——流体、油相、水相黏度，Pa·s；

U ——流体速度，m/s；

t ——时间，s；

P ——流场中的压力，Pa；

g ——重力加速度，m/s2；

F ——外部体积力，N；

αo，αw——油相和水相体积分数。

采用BRACKBILL等［10］提出的连续表面张力（CSF）模型来描述油水两相间的界面张力，其计算公式如下：

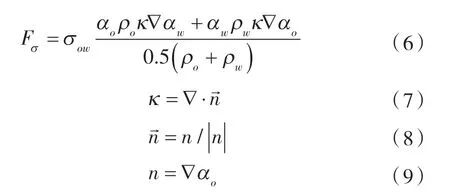
式中 Fσ——油水界面张力，N/m；

σow——油水界面张力系数，N/m；

κ ——界面曲率；

n ——表面法向。

考虑油、水两相黏度及两相在圆管内流动时的操作条件，可发现整个模拟范围内稠油始终作层流流动，水环始终作湍流流动。为此，选用适用于管道中复杂流场计算的标准k-ε模型来描述水环的湍流流动过程，其输运方程如下［11-12］：

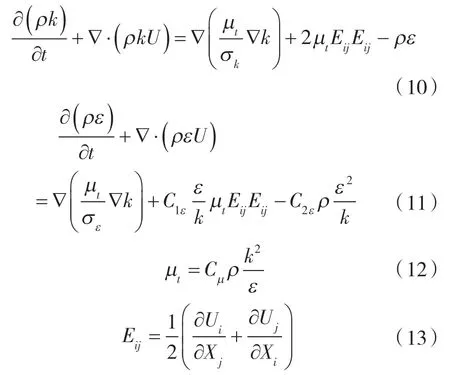
式中 k ——湍动能，m2/s2；

ε ——湍流耗散率，m2/s3；

σk，σε—— 湍动能和耗散率对应的普朗特数，σk=1.0、σε=1.3；

μt——湍动黏度，Pa·s；

C1ε，C2ε、Cμ—— 经验常数，其值分别为1.44，1.92，0.09；

Eij——主流时均应变率；

Ui，Uj——速度在i和j方向的分量，m/s；

Xi，Xj——位移在i和j方向的分量，m。

1.2 几何模型与网格划分

建立如图1所示的圆直管三维模型，其直径D为25 mm，长度L为1 000 mm，稠油入口直径d为21 mm，环空间隙e为2 mm。在入口截面处稠油和水分别被注入管道中心与油壁间的环隙，形成水层包裹核心稠油的同心环状流结构。在计算域内沿管流方向（+Y）选取等间距的5个圆截面（截面Ⅰ～Ⅴ，其位置分别为Y=0～1 000 mm，间距250 mm），用于分析管道不同位置处环状流流动特性与油水两相分布特征。

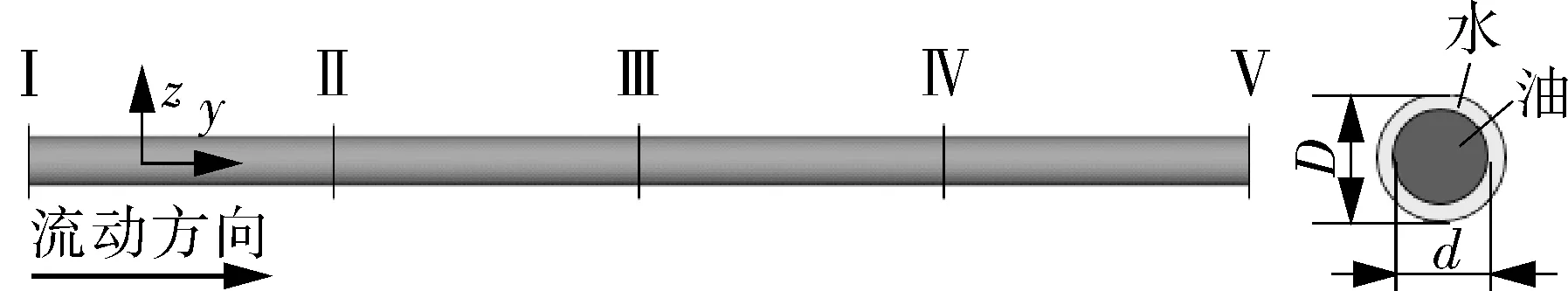
图1 几何模型Fig.1 Geometric model

采用ANSYS MESH模块对管道模型进行多域扫描网格划分。由于模型属于规则的圆柱体，为减少单元数量，提高求解速度，计算区域内的网格全部采用六面体类型。同时对边界层网格进行精细化加密处理，以利于充分捕捉贴近壁面处的流动情况，管道模型的全局及局部网格划分结果如图2所示。

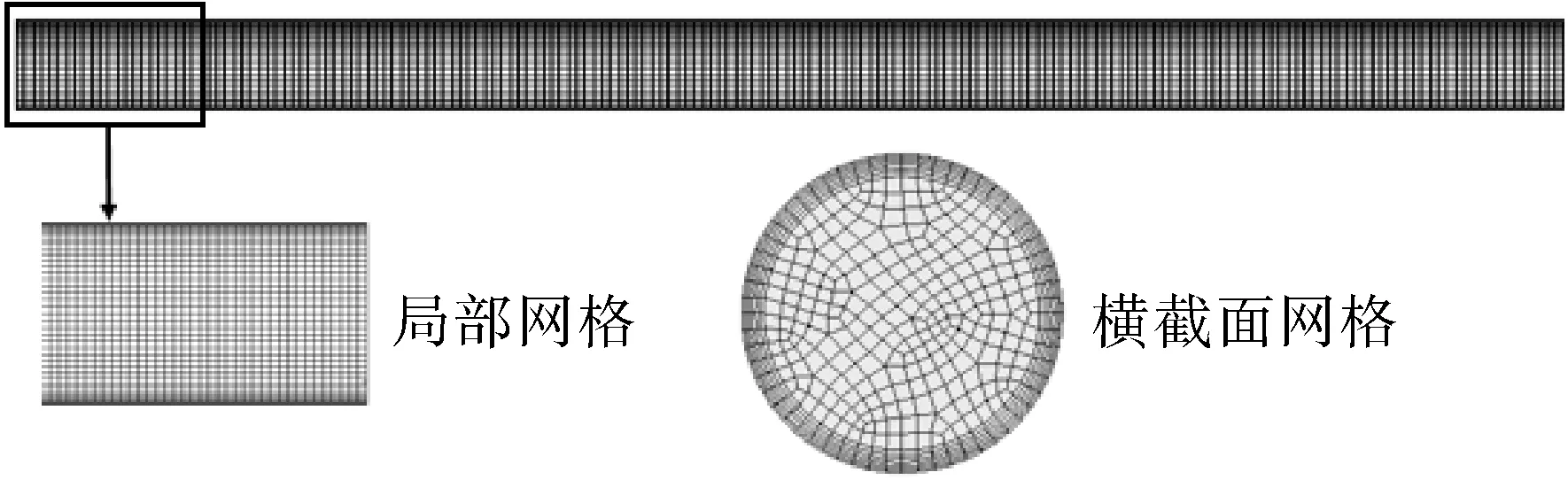
图2 网格模型Fig.2 Mesh model

对不同网格数量下的4套网格进行网格无关性检验，结果如图3所示。网格数量Ne从335 265增加至623 922时不同入口含水率β下截面含油率αo（取截面Ⅰ～Ⅴ的油相体积分数的加权平均值）变化不大，并且模拟值与ARNEY等［12］提出的经验公式计算值具有较好的一致性，可认为所划分的网格已达到网格无关。为在模拟过程中得到较为清晰的油水界面，最终选择体积单元数量为542 921的网格进行后续计算。

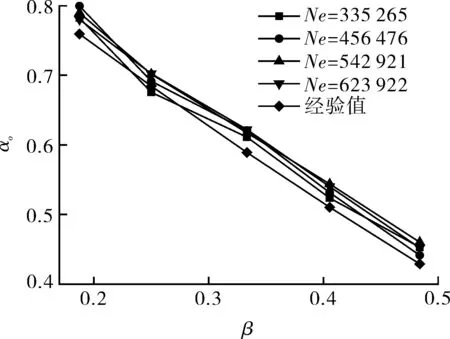
图3 网格独立性验证Fig.3 Grid independence verification

1.3 边界条件与初始条件

边界条件：入口为速度入口边界，Uo=Uw=0.5 m/s；出口为压力出口边界，Poutlet=0.1 MPa；其余均为无滑移壁面边界。初始条件：模拟管内充满水。流体物性参数见表1。

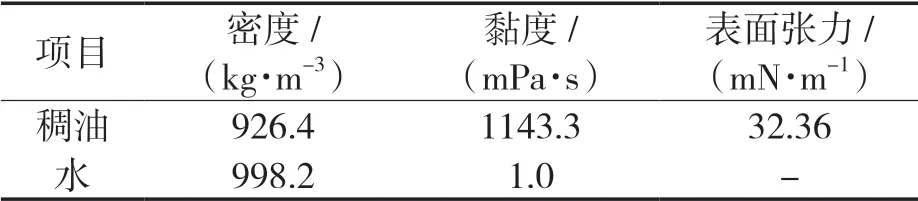
表1 流体物性参数Tab.1 Physical properties of working fluids

1.4 离散方法及收敛准则

模拟类型：基于压力求解器的瞬态模拟，时间步长设为10-3s。求解方法：压力-速度耦合采用PISO算法。离散格式：连续性方程采用PRESTO模式离散，动量方程和湍流方程均采用二阶迎风差分模式离散。收敛准则：输运方程中不同变量的残差低于10-4且管道进出口质量流量相等。

1.5 试验验证

采用自主研制并加工搭建的水环输送稠油减阻模拟装置［6］以验证数值模拟结果的准确性，不同油水表观流速下环状流压降特性的试验与模拟结果如图4所示。可以看出，数值模拟的单位压降都比试验结果要稍高一些，但二者相差小于10.2%且变化趋势一致。这表明本文采用的数学模型及计算方法具有较高的可靠性，可用于油水环状流在管道中的流动模拟。

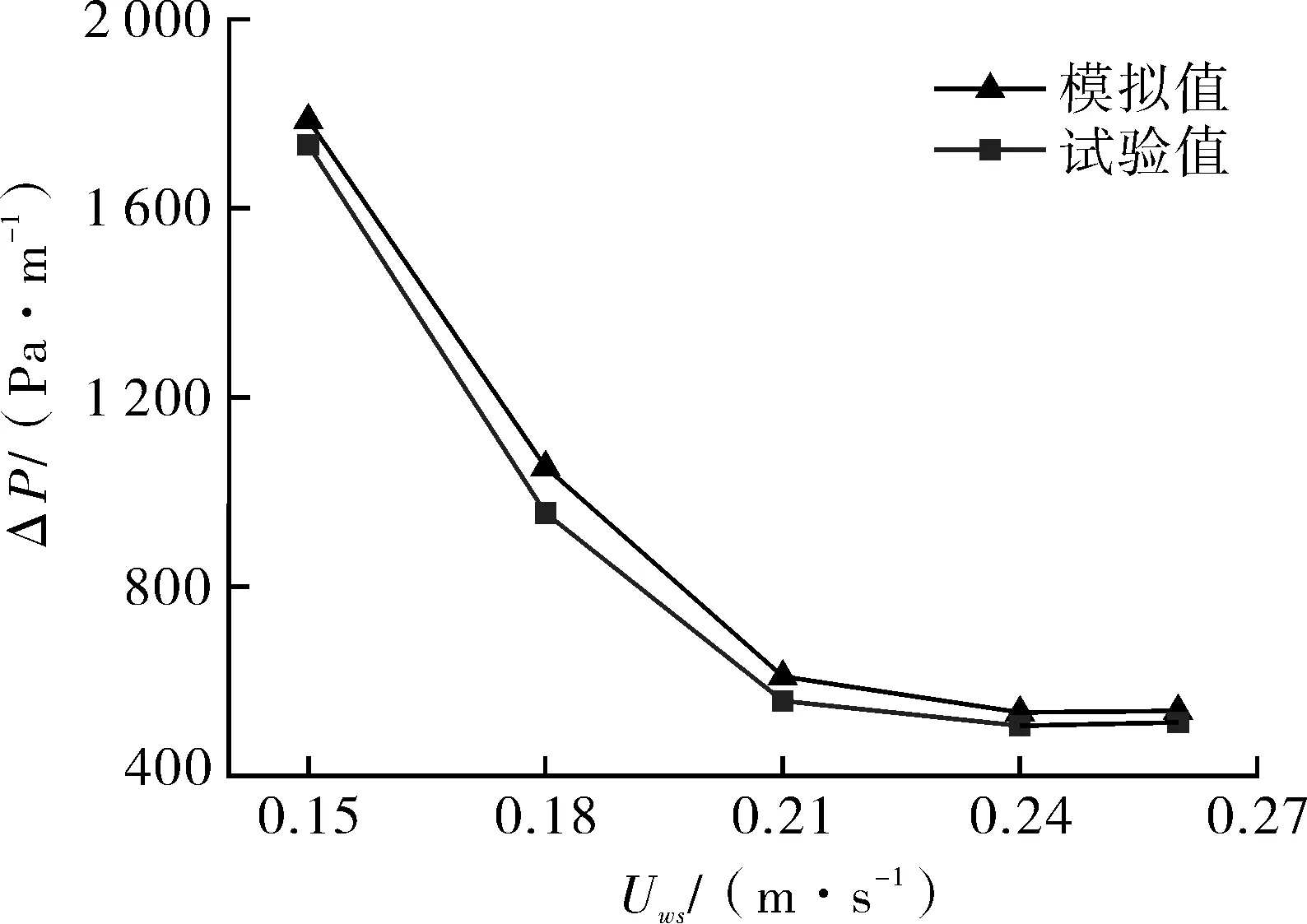
图4 模拟结果与试验数据对比Fig.4 Comparison of simulation results and experimental data

2 环状流的发展变化过程

图5示出油水环状流随时间推移的发展变化过程。起初（t=0 s），管道内全部充满水；随后（t＞0 s），油被注入管道；接着（t=1 s、t=2 s），油水两相沿管流方向逐渐形成水层包裹核心油流的环状流；最终（t≥3 s），环状流在整个管道内形成并达到相对稳定的流动状态。

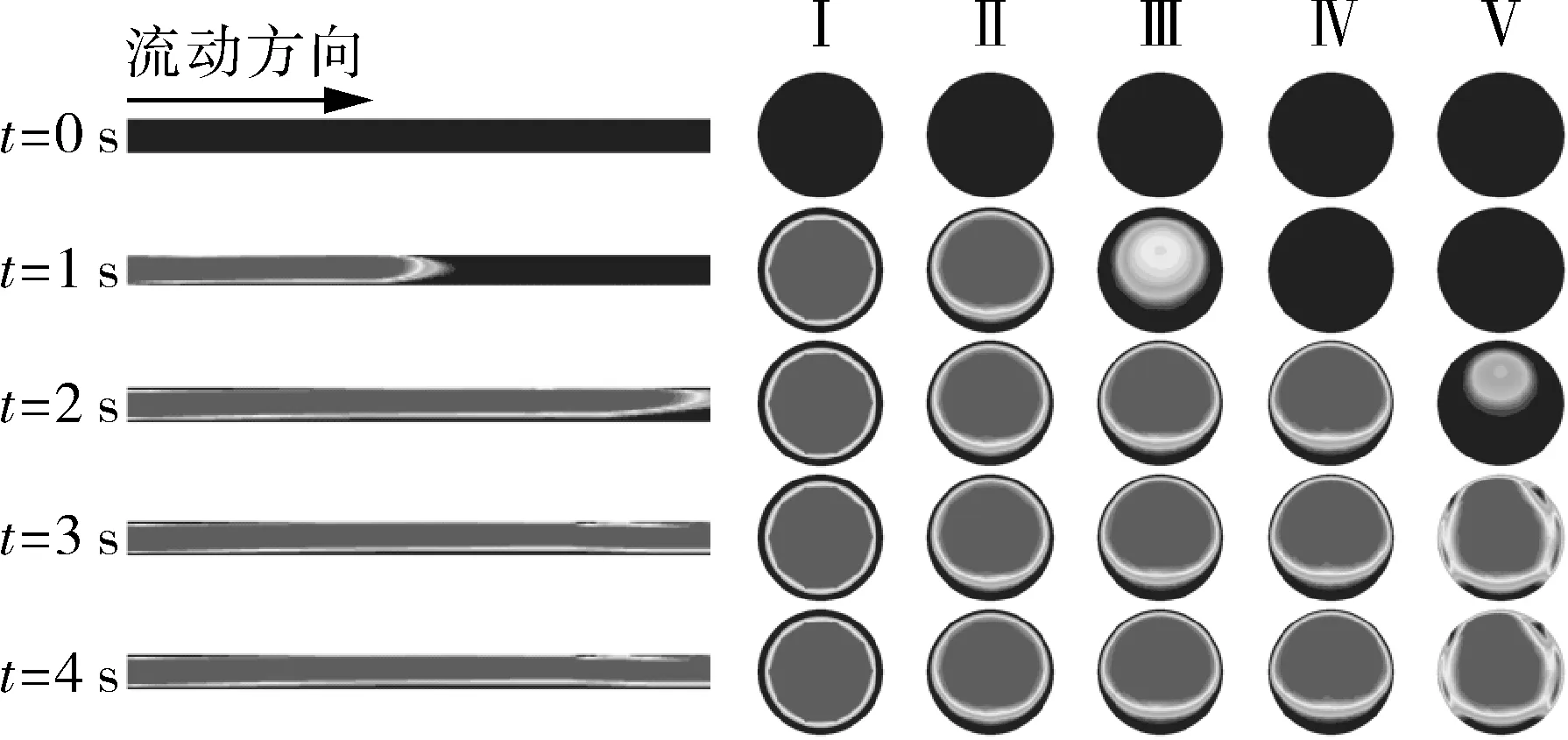
图5 环状流随时间推移的发展变化过程Fig.5 The development process of annular flow over time

在管道入口处（截面Ⅰ），环状流呈同心结构，此时油流位于管道中心，水环均匀分布在油流周围；随着流动距离的增长（截面Ⅱ～Ⅳ），油水两相在密度差的作用下分别上浮与下沉，促使同心流动结构转变为偏心流动结构，此时油流靠近管道上部，水环以上薄下厚的形态分布于油流周围；随着流动距离的进一步增长（截面Ⅴ），油流与管壁接触并黏附于管壁上，致使水环失稳破坏，此时油水交界面上掺混严重，边界轮廓模糊不清；最终，水环被油流完全撕裂，油水两相趋向于分层流动，此时密度较小的油流占据管道上部，而密度较大的水流占据管道下部。

3 结果与讨论

3.1 管壁粗糙度的影响

为探讨管壁粗糙度ε对水环稳定性的影响，在保证其他参数一定的情况下，选取6组管壁粗糙度（ε=0～0.05 mm，间隔0.01 mm）进行模拟分析。

3.1.1 油水两相体积分数分布

不同ε下管道纵截面与横截面Ⅰ～Ⅴ的油水两相体积分数分布如图6所示。由此可见，在各模拟条件下均可形成环状流，且油水两相在管道内的分布特征具有相似性。但环状流不能在整个模拟管段内保持稳定状态，当ε为0～0.05 mm时，其在维持了763，766，768，773，780，785 mm后相继失稳，这说明增大管壁粗糙度能使水环稳定运行距离增长。究其原因，是因为随管壁粗糙度的增大，管壁表面积增加，低黏水相更易吸附在管壁表面的凹坑及沟槽中，有助于增强水膜的水合作用与稳定性［14］，从而使水环维持稳定流动的距离增长。

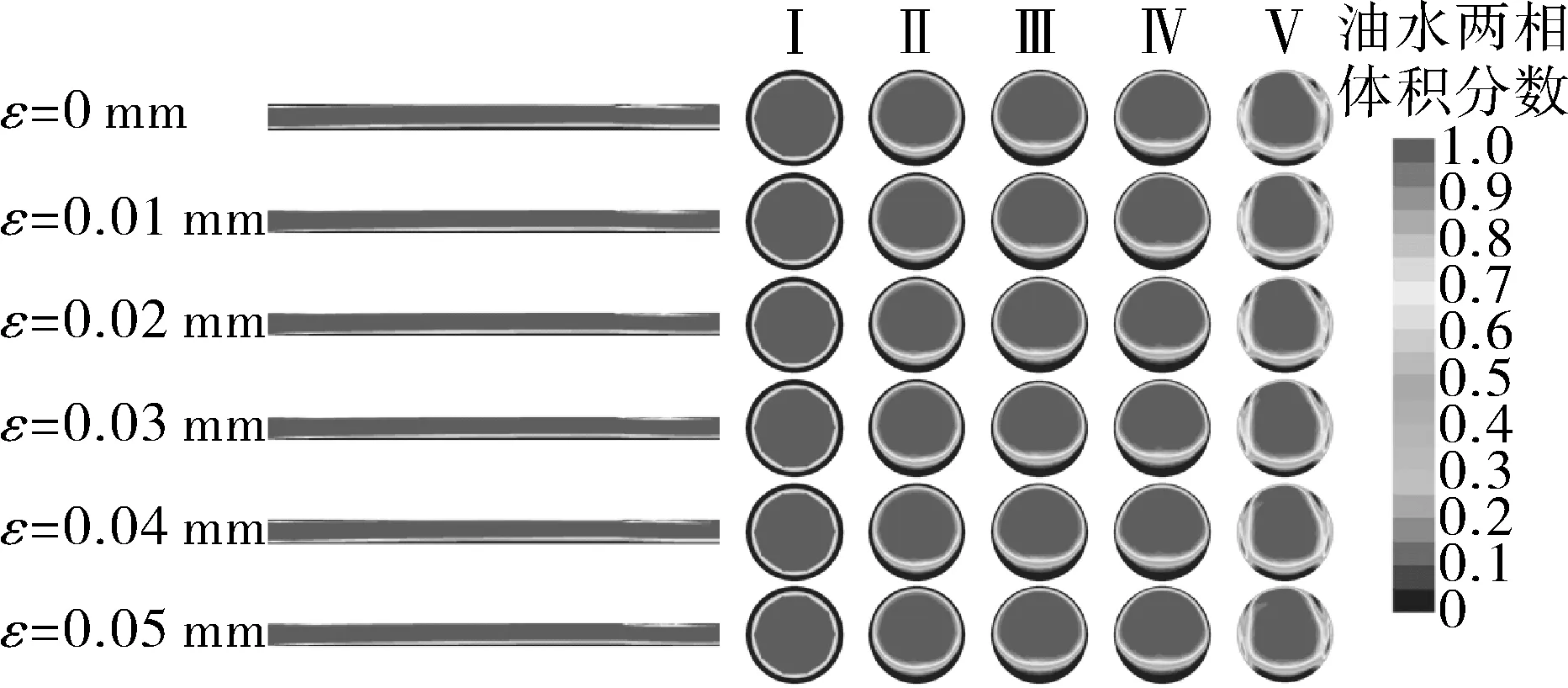
图6 不同ε下管道内油水两相体积分数分布Fig.6 Volume fraction distribution of oil-water two-phase flow in pipe sections under different ε

3.1.2 轴向速度分布

图7示出了不同ε下截面Ⅳ的轴向速度分布曲线。由图7可知，轴向速度几乎不随ε的变化而变化。在无量纲位置为0.95～1区域，环状流流速由0 m/s急增至0.48 m/s；在无量纲位置为-0.77～0.95区域，环状流流速基本持平，保持在0.48～0.54 m/s；在无量纲位置为-0.77～-1区域，环状流流速从0.54 m/s骤降到0 m/s。这表明核心油流区流速基本恒定不变，环形水层区速度梯度很大，剪切主要发生在水层区；且水层区中无量纲位置为0.95～1区域速度梯度较无量纲位置为-0.77～-1区域更大，剪切最强烈，剪切区厚度较小。这是因为油、水密度不同造成核心油流上浮，上浮的核心油流会挤压管道上部的水膜，导致此处的水膜厚度减小，而从管道上部向下运移的水相又会使管道下部的水膜厚度增加。

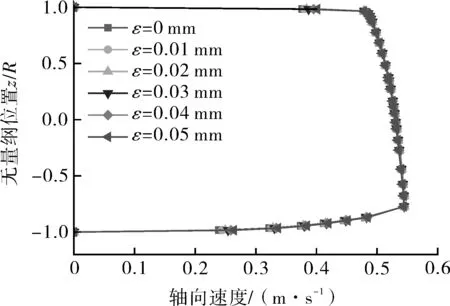
图7 不同 ε下截面Ⅳ的轴向速度分布Fig.7 Axial velocity distribution of section Ⅳ under different ε

3.1.3 总压力分布

不同ε下管道沿线压力变化曲线如图8所示。由此可知，在各模拟工况下管道沿线的压力变化规律基本一致。当环状流在管道中的流动距离从0 mm增加至700 mm时，单位管长压降基本恒定不变，约为400 Pa/m；当环状流在管道中的流动距离从700 mm增加至1 000 mm时，单位管长压降每100 mm变化一次，且越靠近管道出口处，单位管长压降值越大，如ε为0.03 mm时，沿管道出口方向y=700～800，800～900，900～1 000 mm单位管长压降分别为1 082，4 394，8 477 Pa/m。此外，管壁粗糙度越小，单位管长压降值也越大，如ε为0.05 mm时，沿管道出口方向y=700～800，800～900，900～1 000 mm单位 管 长压 降 分别 为961，4 224，8 199 Pa/m，而ε为0 mm时，沿管道出口方向y=700～800，800～900，900～1 000 mm单位管长压降分别为1 238，4 786，8 909 Pa/m，相应于ε为0.05 mm时分别增大277，562，710 Pa/m。这说明当环状流稳定流动时，压力曲线呈平稳趋势，单位管长压降基本恒定不变；当环状流遭到破坏失稳时，压力曲线随流动距离的增长与管壁粗糙度的减小越发陡峭，单位管长压降不断增大，最后趋于稳定。

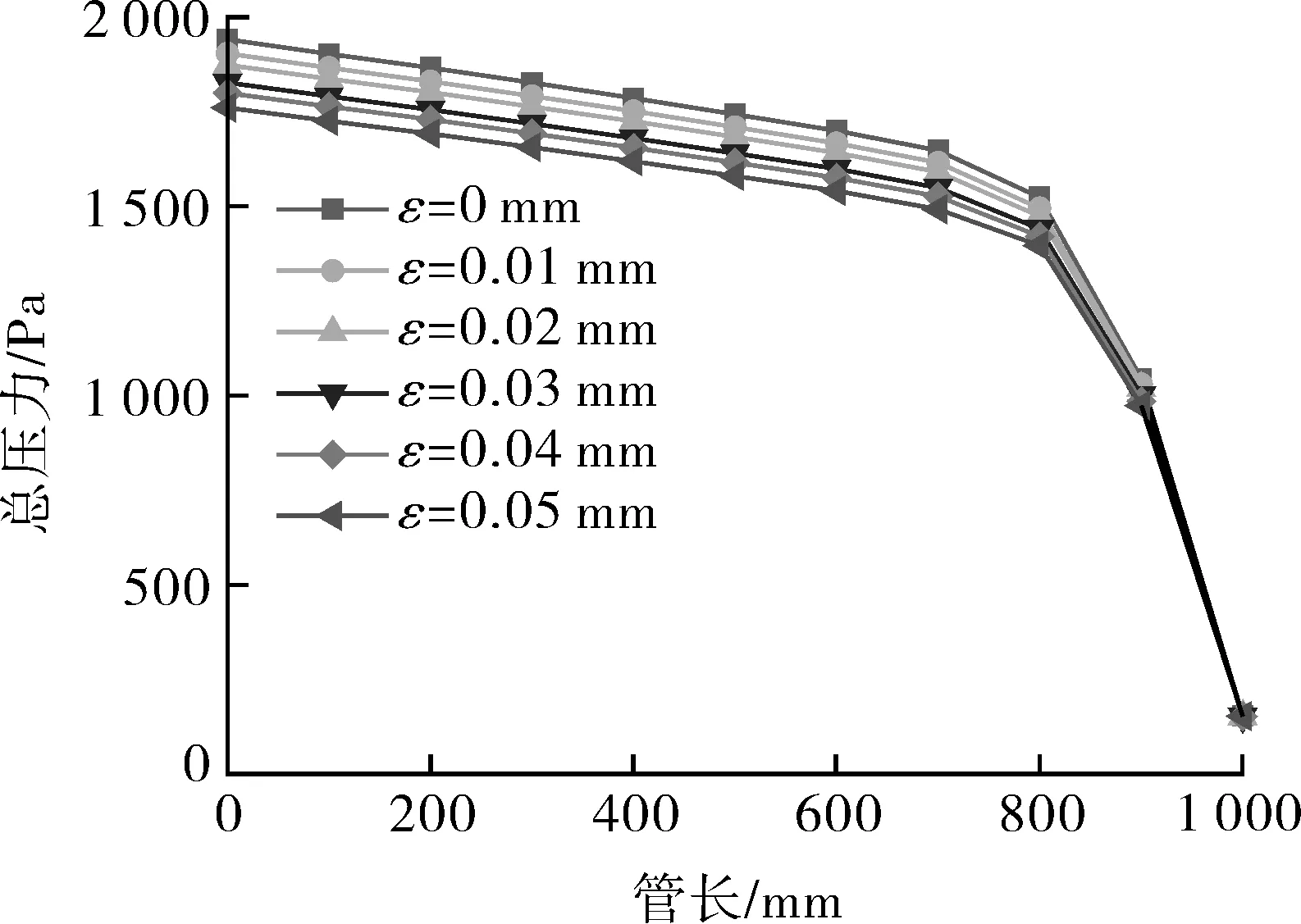
图8 不同ε下管道沿线压力变化曲线Fig.8 Variation curve of total pressure along pipeline under different ε

一般而言，管壁粗糙度的增大会使水环与管壁间的摩擦阻力增大，从而使管道压降升高，而图9中的总压降曲线表现出了与预期完全相反的变化趋势，即管道压降随管壁粗糙度的增大而降低。这是由于管壁粗糙度的增大也会使水环的稳定性增强，继而使管道压降降低。因此，管道压降随管壁粗糙度的变化规律取决于是摩擦阻力还是稳定性占主导地位。在所选工况范围内，水环稳定性占绝对优势，故管道压降随管壁粗糙度的增大而减小。

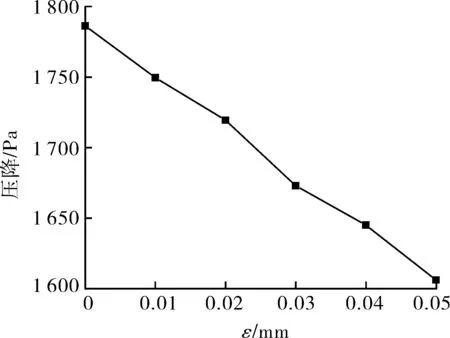
图9 不同ε下管道压降曲线Fig.9 Pressure drop curve of pipeline under different ε

3.1.4 偏心率与持油率

对图6中截面Ⅰ～Ⅴ的油相体积分数与截面Ⅳ的油核偏心率［15］进行定量分析，得到了不同ε下截面平均持油率与油核偏心率的变化曲线如图10所示。从图10可以看出，管壁粗糙度对油核偏心率与截面持油率的影响很小，不同ε下油核偏心率均约为0.73，截面持油率均约为0.74。

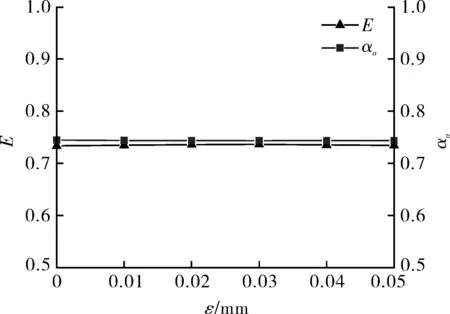
图10 油核偏心率与截面持油率随ε的变化曲线Fig.10 Variation curves of oil core eccentricity and oil holdup with ε

3.2 管壁润湿性的影响

为研究管壁润湿性对水环稳定性的影响，引入管材表面与水的静态接触角θ来衡量［16］，当θ＜90°时，管材表面呈亲水疏油性；当θ＞90°时，管材表面呈亲油疏水性。在保证其它条件不变的情况下，选取5组静态接触角（θ=30°～150°，间隔30°）进行模拟分析。

3.2.1 油水两相体积分数分布

不同θ下管道纵截面与横截面Ⅰ～Ⅴ的油水两相体积分数分布如图11所示。由图11可知，在各模拟条件下截面Ⅰ～Ⅲ的油水两相分布规律相似，而截面Ⅳ～Ⅴ的油水两相分布规律不同，随静态接触角的增大，油水交界面处的掺混扰动增强，两相边界的清晰程度减弱。由管道纵截面的油水两相体积分数分布特征可知，环状流在管道中运行一段距离后逐渐失去水环包裹核心油流向管道出口方向流动的状态，当θ为30°～150°时，其维持稳定流动的长度分别为864，825，763，710，663 mm，这表明增大静态接触角会使水环稳定运行距离缩短。这是因为随静态接触角的增大，管材表面的亲油性增强，亲水性减弱，即管材表面由易被水附着转变为易被油附着，且在流动过程中被水层剪切剥离的油滴易黏附在管壁上，难易被水流带走，造成水环的稳定性下降，从而使水环维持稳定流动的距离减短。

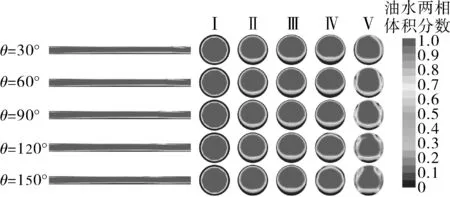
图11 不同θ下管道内油水两相体积分数分布Fig.11 Volume fraction distribution of oil-water two-phase flow in pipe sections under different θ

3.2.2 轴向速度分布

图12示出了不同θ下截面Ⅳ的轴向速度分布曲线。从图12可以看出，轴向速度随静态接触角的变化而变化。当 θ 较小时（30°～90°），截面Ⅳ的轴向速度关于中心线基本呈对称分布，具体描述参见第3.1.2节。当 θ 较大时（120°和150°），截面Ⅳ的轴向速度呈舌头状分布。相比于静态接触角较小时的情况，管道上部环形水层区速度梯度与核心油流区速度都有所减小，而管道下部环形水层区速度梯度与核心油流区速度都有所增大。这是由于水环失稳破坏后，高黏油相黏附在管壁上，尤其是管顶和两侧壁面，使得环形水层区速度梯度与核心油流区速度重新分布。

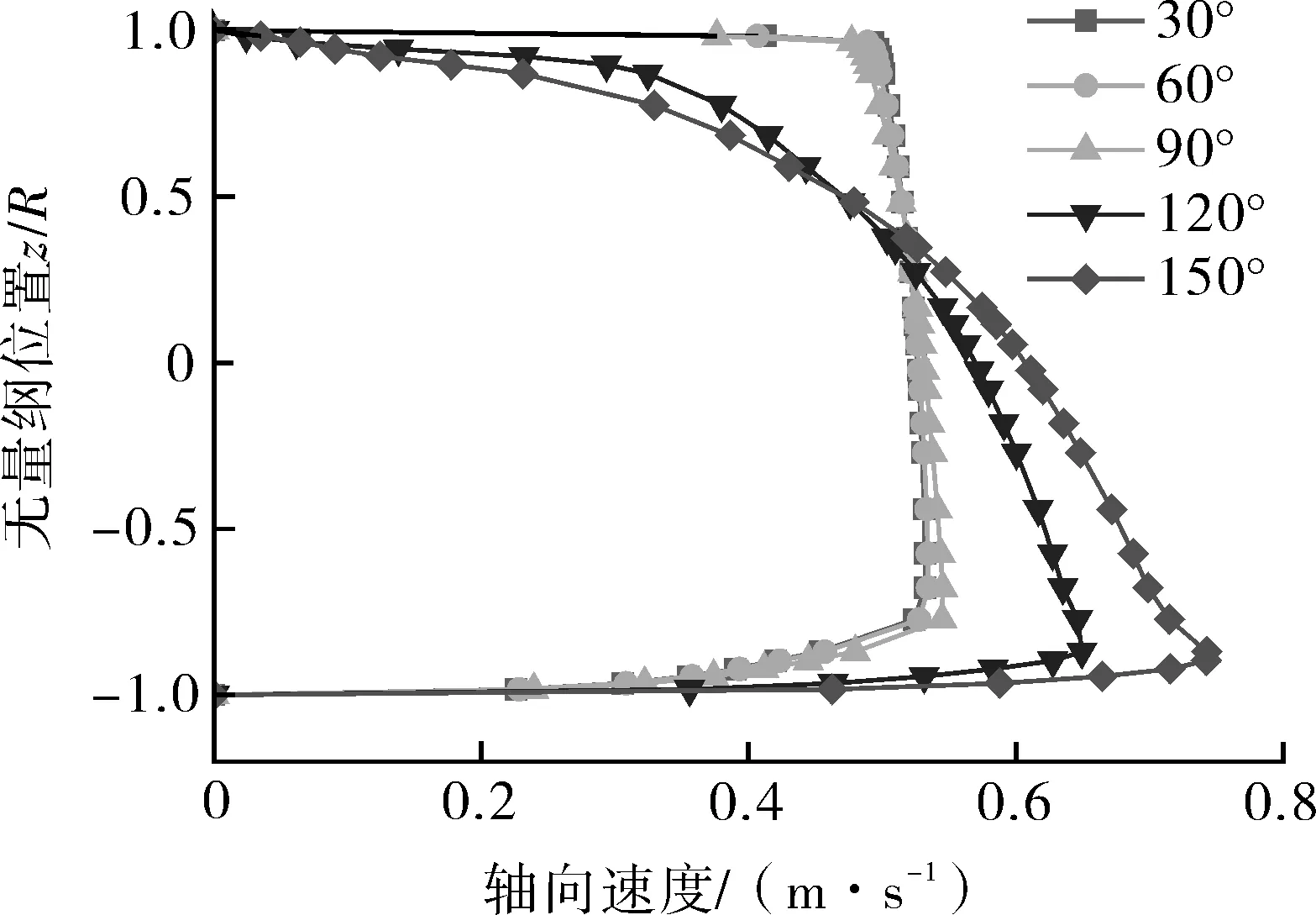
图12 不同 θ 下截面Ⅳ的轴向速度分布Fig.12 Axial velocity distribution of section Ⅳunder different θ

3.2.3 总压力分布

不同θ下管道沿线压力变化曲线如图13所示。由此可知，单位管长压降保持恒定的流动距离随静态接触角的增大而减短，其由 θ 为30°和60°时的800 mm先减短到 θ 为90°和120°时的700 mm，再减短到 θ 为150°时的600 mm。超过前述流动距离后，单位管长压降每100 mm变化一次，且越靠近管道出口处，单位管长压降值越大，如 θ 为90°时，沿管道出口方向y=700～800，800～900，900～1 000 mm单位管长压降分别为1 082，4 394，8 477 Pa/m。此外，静态接触角越大，单位管长压降值也越大，如θ为30°时，沿管道出口方向y=800～900，900～1 000 mm单位管长压降分别为1 144，4 013 Pa/m，而θ为60°时，沿管道出口方向y=800～900，900～1 000 mm单位管长压降分别为2 233，6 476 Pa/m，相应于θ为30°时分别增大1 089，2 463 Pa/m。通过分析不同静态接触角下的管道进出口压力可知，管道总压降（见图14）随静态接触角的增加而增大。这说明当管材表面呈亲水疏油性时，管道总压降最低，单位管长压降保持恒定时的流动距离最长，单位管长压降变化时的降幅最小。也就是说，当管材表面呈亲水疏油性时，水环的稳定性最好。

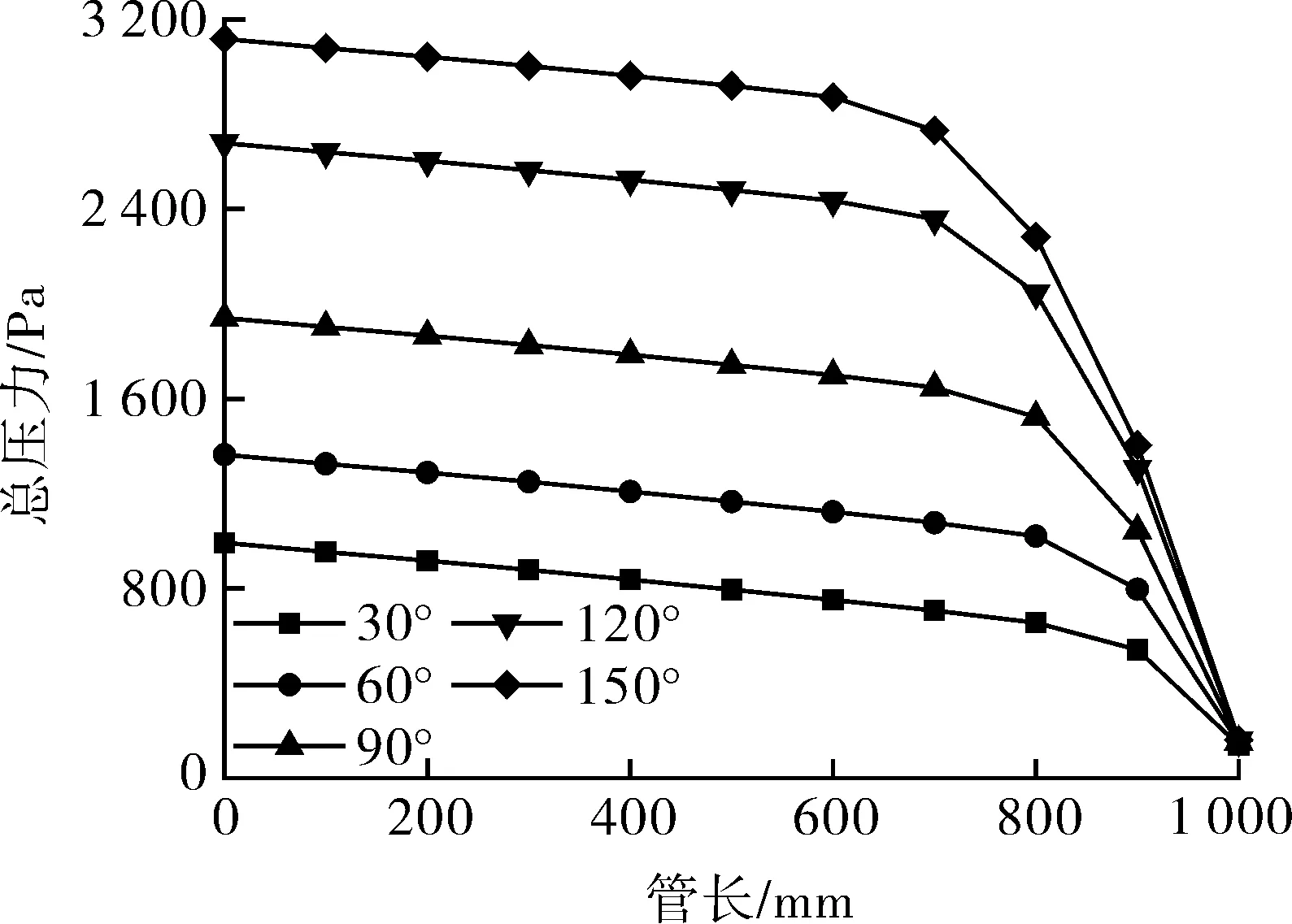
图13 不同θ下管道沿线压力变化曲线Fig.13 Variation curve of total pressure along pipeline under different θ

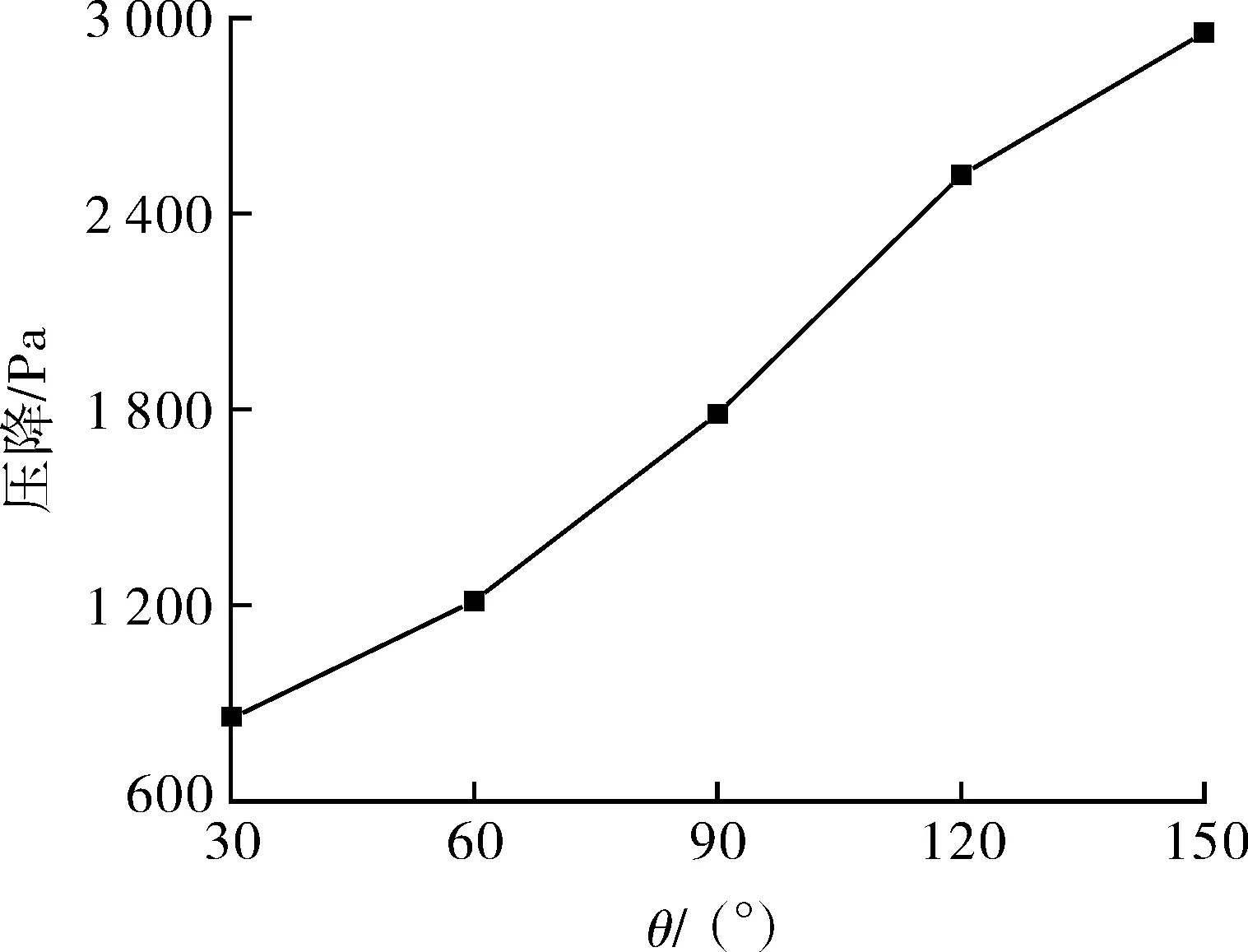
图14 不同θ下管道压降曲线Fig.14 Pressure drop curve of pipeline under different θ

3.2.4 持油率与偏心率

对图11中截面Ⅳ的油核偏心率与截面Ⅰ～Ⅴ的油相体积分数进行定量分析，得到了不同θ下油核偏心率与截面平均持油率的变化曲线如图15所示。从图15可以发现，静态接触角对油核偏心率的影响较大，当θ为30°～90°时，核心油流上浮偏心程度较小，油流完全被限制在水环内部，不会与管壁接触，此时油核偏心率均约为0.73；当θ增加至120°和150°时，核心油流上浮偏心程度增大，水层不再包裹油流，油流接触管壁，此时油核偏心率均为1.0。相反，静态接触角对截面持油率的影响很小，不同θ下截面持油率均约为0.74。

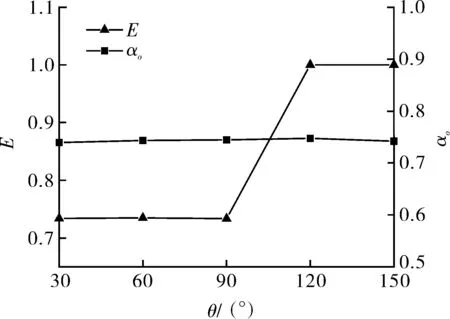
图15 油核偏心率与截面含油率随θ的变化曲线Fig.15 Variation curves of oil core eccentricity and oil holdup with θ

4 结论

（1）油水环状流在流动过程中并不能一直保持稳定的流动状态，随着流动时间和运行距离的增长，其先由同心环状流动（油流被厚度均匀的水环包裹位于管道中心）转变为偏心环状流动（油流被上薄下厚的水环包裹位于管道中上部），再转变为不完全环状流动（油流不能被失稳破坏的水环完全包裹，其与管壁接触），最终趋向于分层流动（上层为高黏油，下层为低黏水）。

（2）随着管壁粗糙度的增大，水平管中水环结构的稳定性增强，但管壁粗糙度的增大通常会使管道总压降升高。因此在实际输送过程中，应综合考虑管壁粗糙度对水环稳定性和管道总压降的影响，选取适当的管壁粗糙度以保证水环稳定性处于较高水平的同时，管道总压降处于较低水平。

（3）当管材表面与水的静态接触角较小时，即管材表面呈亲水疏油性时，水平管内水环结构的稳定性较强。故可采用物理或化学方法改变现场使用管材的亲疏水性能，使其内表面呈亲水疏油性，以提高水环的稳定性，同时抑制高黏油在管壁的黏附。