面向双保证率的水库供水能力优化计算方法研究

林鹏飞，游进军，蒋云钟，贾 玲，付 敏

（中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室，北京 100038）

1 研究背景

水利工程供水能力是指满足一定供水保证率的最大供水量，体现工程保障民生、支撑经济发展的能力，是水利规划管理的重要依据。随着城市化进程的推进和生态文明理念的深入，许多水利工程面临从单一的农业灌溉任务向多目标供水任务转变［1］。由于供水目标优先级和保证率要求不同，多目标水库工程供水能力分析十分必要［2］，在实际工作中对合理确定水厂规模、保障城市供水安全具有重要意义。

传统的水库供水能力针对单一供水目标，分析方法主要为典型年法和长系列调节法［3-6］，难以有效处理多目标、多保证率问题［7］。多目标水库供水计算通常需要依据一定的调度规则，已有学者采用智能优化算法求解多目标水库调度规则。尹正杰等［8］设计了一种水库多目标供水调度规则，并基于模拟和遗传算法耦合的方法构建了水库多目标供水调度模型。王学斌等［9］基于改进NSGA-Ⅱ方法以经济用户综合缺水量最小、生态缺水量最小、发电量最大为目标对黄河下游小浪底-西霞院两座水库的多目标调度进行了研究。Simona Consoli等［10］基于非线性优化方法（NLP）对以灌溉为主的多目标水库运行规则进行了优化。游进军等［11］提出了在水量调控基础上进行工程调度的二层结构流域生态调度模型，以供水量最大为目标实现了对调度规则的优化。上述研究均基于预定需水优化调度规则，提出缺水量最小或效益最大为目标的供水方案，缺少对以满足保证率要求为目标的工程供水能力分析。

供水保证率是表征用户供水安全的重要指标，不同类型用户的保证率要求不同，因此满足差异性保证率要求是计算水库供水能力的必要条件。部分学者开展了考虑保证率要求的水库调度计算。伍远康等［12］以生产、生活、生态用户期望供水保证率与计算保证率之差的平方和最小为目标，提出了基于保证率要求的水库供水限制水位核定方法。尹正杰等［13］以保证率最大和缺水量最小为目标，利用多目标遗传算法求解水库综合利用的优化调度图。艾学山等［14］以满足保证率要求为约束条件，以发电量最大、灌溉需水和生态流量满足程度最高为目标构建了水库多目标调度模型。黄显峰等［15］以发电保证率、出力等为约束条件，提出了水库调度图多目标优化方法。张连鹏等［16］以不同用户保证率作为约束条件，构建了面向生态的水库群中长期调度优化模型，制定了额尔齐斯河关键水库的生态调度图。季海萍等［7］依据调度线控制进行长系列调算，根据经验试算选择合理的调度线，实现不同用户保证率目标的水库供水能力求解，但不能保证结果是满足保证率要求的最大供水量。根据上述研究，考虑保证率的优化调度有两种方式，一种是将多个用户保证率转化为单一目标优化，另一种是将保证率要求作为约束条件优化调度规则。现有方法一定程度可以解决满足保证率要求的调度优化，但存在计算保证率可能高于要求值、用户优先关系不明晰等问题，不能确定满足不同用户保证率要求的最大供水量作为供水能力。

综上分析，多用户保证率水库供水能力计算有三方面要求：一是满足不同用户的保证率；二是需要优化调度规则协调不同用户之间的供水关系；三是确保得出的供水能力是满足要求的最大供水量。当前仍缺乏满足多保证率要求的水库供水能力计算方法。针对上述要求，本文提出了面向双保证率的水库供水能力优化计算方法。外层基于粒子群算法对水库调度规则进行整体优化，内层通过迭代计算寻求给定规则下满足保证率要求的供水能力，内、外层嵌套实现调度规则和供水能力的同步优化，可为相关研究和实际工作提供借鉴和参考。

2 计算方法

2．1 设计思路 工程供水能力随用户类型变化的主要原因在于供水保障要求（就水量而言主要是供水保证率）不同。其次，用户需水的过程性差异也会带来影响，如年际、年内过程变化的农业灌溉与过程均匀的城镇供水导致不同计算结果。本文重点分析城镇供水和农业灌溉两类具有不同保证率要求的供水能力计算方式。从数学角度分析，求解两类具有差异性目标的用户供水能力，需要明确其中一个用户的保障目标才能优化，否则只能得出非劣解集，无法给出确定结果。此外，实际管理中通常也需要分析某一用户需求变化对其他用户的影响。因此，本次研究先设定农业需水，计算满足两类用户保证率目标的最大城镇供水量作为城镇供水能力，并将农业需水作为农业供水能力，从而得出满足双保证率要求的水库供水能力。在此基础上，通过调整农业供水保证率和农业需水分析两类用户供水能力和供水量的转换关系，反映农业保障目标变化对城镇供水能力的影响。类似也可以先设定城镇供水目标分析农业供水能力计算结果，为不同的决策需求提供分析方法。

水库供水能力计算受调度规则约束，二者具有层级从属关系，必须协同优化才能得出合理可信的结果［17］。设置农业调度线（库容控制值，以下简称调度线，即高于该库容的蓄水才能向农业供水）作为调度规则，对城镇供水和农业灌溉的竞争关系进行调控，在优先保障生态基流后按城镇供水能力目标值供水，再根据水库蓄水量按调度线控制可供水量满足农业需求。根据二层系统决策理论，首先需在上层确定决策变量，下层子系统在上层边界条件下根据自身偏好优化目标，上层再根据下层的最佳反应在可行范围内分析整体最优决策［18-19］。按照上述理论，在农业供水任务确定的条件下，设计内、外双层嵌套的水库供水能力优化计算方法，分别对应二层系统决策的下层和上层。外层为基于粒子群算法的调度规则优化，以调度线为决策变量、城镇供水能力最大为目标。粒子群算法结构简单、收敛较快，针对水库调度规则的优化具有一定优势［20-22］。内层为满足多保证率约束的供水能力迭代计算，以外层的调度线为输入参数，以城镇供水能力可行区间上下界为决策变量，基于定界迭代方法确定该条调度线控制下满足双保证率要求的城镇供水能力最大值，并反馈给外层，外层种群进化收敛后得出调度线和供水能力最优结果。计算流程如图1所示。由于城镇需水过程一般较为稳定，城镇供水能力按长系列等流量法进行计算［23-24］。

图1 水库供水能力优化计算流程

2．2 目标函数 以城镇供水能力最大为内、外层优化的目标：

式中：Qoue为第e代调度线种群对应的最大城镇供水能力，e为当前进化代次；为调度线个体（）对应的最大城镇供水能力；n为调度线个体序号；为第e代第n条调度线个体；N为种群规模；f（）为针对调度线个体得出的满足保证率要求的城镇供水能力的计算过程。

2．3 决策变量

（1）外层以调度线为决策变量，年内每个计算时段的调度线称为粒子，用符号表示，m为所在的年内计算时段。年内所有月份调度线粒子组成调度线个体本代所有调度线个体组成调度线种群，可用矩阵Le表示：

式中M为年内总计算时段数，若以月为计算时段则M为12。

（2）内层以城镇供水能力可行区间上下界作为决策变量，分别为Qsmax、Qsmin。内层通过不断缩小可行区间寻找满足供水保证率要求的最大城镇供水能力。

2．4 约束条件 主要为供水保证率、生态流量、水量平衡、库容约束、供水约束等。

（1）供水保证率约束：

式中：Purob和Parob分别为设定的城镇和农业目标保证率，采用年保证率；Purca和Parca分别为城镇和农业用户计算得出的保证率，可根据式（4）确定：

式中：Y为长系列计算的总年份数；yur为城镇用户未产生破坏的年份数；yca为农业用户未产生破坏的年份数。

（2）生态流量约束：

式中：Weci为第i时段的生态下泄水量；Deci为第i时段生态基流。

（3）水量平衡约束：

式中：Vendi为第i时段末水库蓄水量；Vendi-1为第i-1时段末水库蓄水量；Wini为第i时段的入库水量；Wloi为第i时段的水库漏损及蒸发量；Weci为第i时段的满足生态下泄水量；Wuri为第i时段的城镇供水量；Wari为第i时段的农业供水量；Wfli为第i时段末超过最大蓄水库容限制的下泄水量。

（4）库容约束：

式中：V mini为第i时段水库死库容；V maxi为第i时段水库蓄水库容上限（汛期为汛限水位对应库容，非汛期为正常蓄水位对应库容）。

（5）供水约束：

式中：Duri为第i时段城镇用户需水量，在计算过程中即为城镇供水能力值；Dari为第i时段农业用户需水量，要求各用户供水量不能超过其需水量及供水渠道最大过水量。

2．5 求解步骤 结合内、外层模块功能和优化计算思路，外层主要包括生成初始调度线、调度线初筛、比选个体极值和全局极值、更新进化速度和方向、调度线种群进化等步骤，内层主要包括确定城镇供水能力可行区间和定界迭代等步骤，内、外层实现嵌套计算的具体步骤如下：

（1）外层：随机生成初始调度线种群，如式（2）所示。

（2）外层：调度线初筛。本步骤可以剔除不能满足保证率要求的调度线个体，提高计算速率。若生成的调度线个体位置过高，即使不向城镇用户供水也无法满足农业目标保证率要求，则该条调度线个体不合理，予以剔除。需要指出，剔除的调度线个体不参与本代的内层计算，但仍参与外层的种群进化，从而保证种群规模不变。

（3）内层：确定可行区间。基于步骤（2）输入的调度线个体，根据式（9）初步确定城镇供水能力可行区间，可以限定寻优范围减少迭代次数：

（4）内层：定界迭代。基于定界迭代法［25-26］和对分差值算法［27］缩小供水能力区间，以迭代区间中值作为本次试算的供水能力值，然后根据保证率结果缩小城镇供水能力可行区间，上下界逼近收敛时即得出调度线个体对应的城镇供水能力值。迭代试算的城镇供水能力值依据式（10）确定：

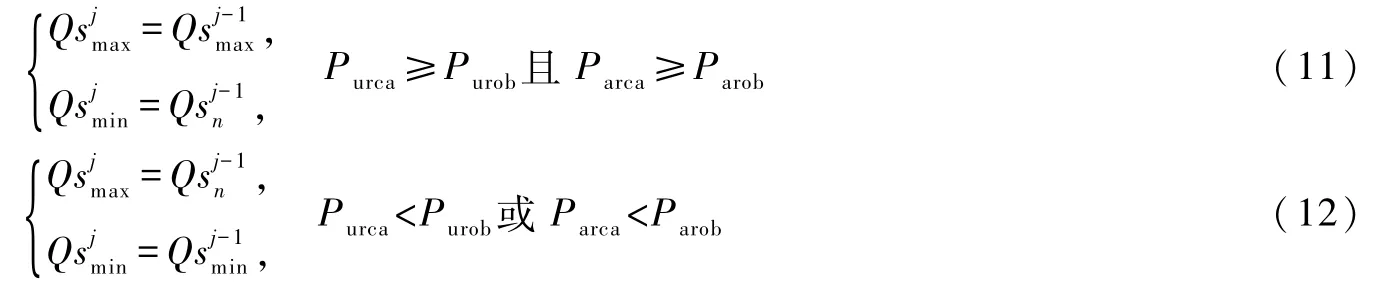
根据式（11）、式（12），当城镇和农业保证率均满足时表明城镇供水能力可以继续增加，可行区间取现有可行区间的上半区。其他情况下该调度线不能同时满足两个保证率的要求，必须降低城镇供水能力目标值减少两个目标的竞争关系，可行区间取现有区间的下半区。

（5）内层：调度线个体循环判断。根据式（13）判断调度线个体对应的城镇供水能力是否达到最大：

当城镇供水能力定界区间范围小于精度控制值δ（一般取非常小的常数）则停止迭代并进入步骤（6），并以作为第n条调度线个体在第e代对应的城镇供水能力，如式（14）所示：

若不符合迭代停止条件，则重复步骤（4）调整迭代区间。

（6）内层：调度线种群循环判断。判断当前进化代次的种群是否均完成城镇供水能力计算，若未完成则进入步骤（3），计算下一条调度线个体对应的城镇供水能力。若全部调度线种群完成计算则结束内层循环，并将本代所有调度线个体对应的城镇供水能力返回外层，进入步骤（7）。

（7）外层：比选个体极值和全局极值。通过比选第n条调度线个体在不同代次对应的城镇供水能力确定调度线个体极值（）；通过比选截止到当前代次所有种群对应的城镇供水能力确定调度线全局极值）。

（8）外层：收敛判断。当最大城镇供水能力（全局极值）保持不变，且连续达到一定进化代数，一般应达到50次以上，可认为算法已经完全收敛，结束计算，并输出最优全局调度线和供水能力。若不满足收敛条件，则继续执行步骤（9）。

（9）外层：更新进化速度和方向。根据式（15）更新下一代调度线个体的进化速度和方向：

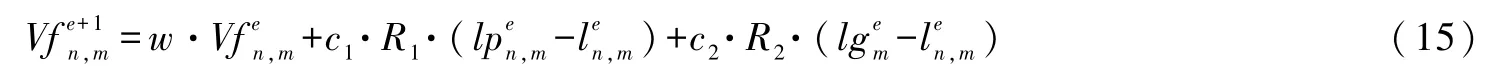
（10）外层：调度线种群进化。根据粒子群算法的种群进化方法，调度线进化过程如下：

并将生成的调度线种群带入步骤（2），进行下一代计算。

3 实例应用

3．1 实例概况 赤田水库是三亚市主要水源工程，位于藤桥西河下游，坝址以上集雨面积221 km2，多年平均入库水量约2．34亿m3（含上游跨流域调水补充），总库容7710万m3，兴利库容4740万m3，死库容1220万m3，正常蓄水库容非汛期（11月—次年5月）为5960万m3，汛期（6—10月）考虑汛限水位限制为5081万m3。赤田水库供水任务包括城镇用水、农业灌溉和生态用水，由于城市发展和节水技术提升，农业灌溉面积和用水需求均低于设计值，而城镇供水任务超过设计预期。为确定合理的城镇规模，采用双层优化方法计算保障农业和生态目标下的城镇供水能力。

3．2 水库综合利用要求 根据现有灌溉面积和定额，赤田水库灌区50%、75%、90%降水频率年的农业需水量分别为1249万m3、1383万m3、1603万m3，多年平均为1340万m3，年内分布过程如表1所示。根据规划确定的藤桥西河生态流量要求，设置水库生态基流为0．2 m3/s。城镇保证率目标为95%，满足保证率目标的农业多年平均需水作为农业供水能力。

表1 不同频率年农业需水年内分布过程 （单位：万m3）

3．3 模型参数设置 外层优化需设置粒子群算法相关参数，本文种群规模设为500，结束优化的目标值连续不变代数设为50代，进化速度的变化区间设为［-100万m3，100万m3］，初始在区间内随机生成，进化过程中的根据式（15）更新。c1和c1均取值为2，w的区间为［0．4，0．9］。参考兴利库容值内层计算模块迭代步长T设为400万m3，结束循环判断精度δ设为0．0001。

3．4 结果分析与讨论

3．4．1 优化方法可行性分析

（1）城镇供水能力进化过程分析：选用1956—2010年月过程入库水量系列，在农业保证率90%条件下按照种群规模为100和500分别进行5次计算，城镇供水能力进化过程如图2所示。种群规模为100时平均需33．2代达到最大供水能力，种群规模为500时平均需18．4代，说明种群规模较大时达到收敛的代数更少。不同种群规模收敛时的城镇供水能力均为642．5万m3/月。种群规模较小时经过足够多代次的进化仍然可以达到同样的目标值，表明双层优化方法的收敛性较好。

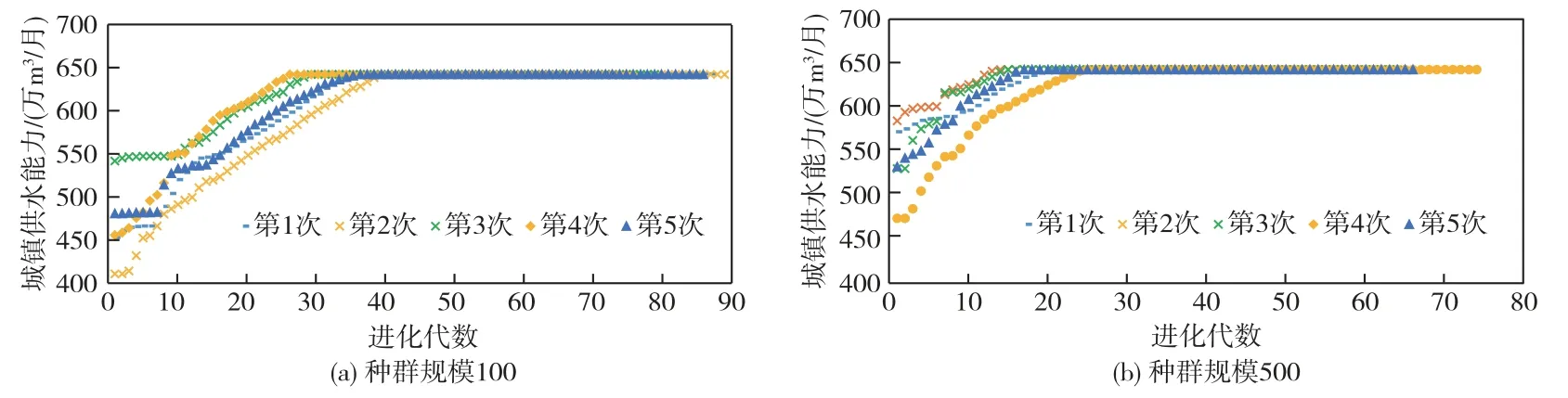
图2 不同种群规模条件下城镇供水能力进化过程

（2）调度线分布型态合理性分析：对比农业保证率分别为90%、75%、50%的调度线结果（图3），可以看出农业保证率越高，计算得出的调度线值越低。分析表明，高于调度线的蓄水可用于农业灌溉，调度线较低时更多水量可保证农业需求，同时也会降低城镇供水的保障能力，说明提高农业保证率必然需要更大的库容保障，加剧与城镇供水矛盾。从年内分布来看，汛期调度线整体呈上升趋势，枯水期呈下降趋势。由于汛期来水较多，农业相对容易满足，提高调度线有利于增加汛后蓄水量，增强枯水期城镇供水保障。此后，枯水期来水少且农业需水增加，必须逐步降低调度线提高农业保障。

图3 不同农业保证率条件下调度线年内分布

3．4．2 计算结果分析

（1）供水能力与保证率关系分析：根据不同农业保证率目标的计算结果（表2），在农业保证率为50%和90%时，城镇供水能力分别为8594万m3/a和7710万m3/a，总供水能力分别为10 284万m3/a和9400万m3/a，随着农业保证率提高城镇供水能力和总供水能力均下降。

表2 不同农业保证率要求的水库供水能力和供水量

农业保证率变化下的城镇和农业用户的供水能力和供水量转化关系如图4所示。农业保证率目标较小（小于30%）时，城镇供水能力几乎不受其变化影响。进一步提高农业保证率后城镇供水能力小幅下降，超过50%后下降幅度加大。当农业目标与城镇同样达到95%时，水库总供水能力和供水量均低于仅保障城镇供水时的能力和供水量。说明二者的竞争关系随着农业保证率提高而加剧，在同样保证率要求下具有过程性要求的农业供水保障难度高于城镇供水。分析原因表明，在农业保证率目标较低时，在丰、平、枯不同来水年份均可破坏，而城镇供水仅在特枯水年份允许破坏，二者竞争关系不明显。当农业保证率目标提高，必须满足枯水年的需求时，同等竞争导致城镇供水能力明显下降。

图4 供水能力、供水量与农业保证率关系

提高农业保证率后城镇供水量有所下降，总供水量先增后减。其原因在于城镇供水保障要求更高，在考虑保障目标较低的农业供水后总供水量增加。由于农业需水的非均匀过程且与来水不一致，当农业供水保证率提高到超过50%后，对城镇供水挤占效应加剧，虽然农业供水量增加，但城镇供水量下降更多，水库总供水量也逐步下降。

（2）供水能力与农业需水量关系分析：分析农业需水量变化对水库供水能力的影响，计算结果见表3。通过调整灌溉面积改变需水总量，年内过程保持不变。总体上，城镇供水能力和供水量随农业需水增加而减少，但总供水能力和供水量增加，反之亦然。当农业需水下降20%时农业供水量为1017万m3，与表3中农业保证率为50%的农业供水量（1030万m3）基本一致，但城镇供水能力偏低675万m3/a。说明同样的供水效果下，降低农业保证率比降低农业需水更有利于提高城镇供水能力。分析表明，压缩灌溉面积虽然减少了农业总需水量，但农业需水过程特征并未改变，因此对枯水年农业用水高峰期的供水矛盾缓解作用不明显。而降低农业保证率目标允许在枯水年破坏农业灌溉保证城镇需求，更有利于城镇供水能力的提升，但农业破坏程度也会加大。进一步分析表明，农业需水年内过程变化也会带来供水能力计算结果的变化。上述分析说明，保证率目标是水库供水能力的决定性因素，而解决枯水期供水矛盾和用户竞争关系是提升工程供水能力的关键。

表3 农业保证率90%不同农业需水条件下的供水能力与供水量

4 结论

多目标水库供水能力受调度规则和用户保证率影响，协调不同保证率要求的水库供水能力分析可更准确预判供水目标的保障关系，寻求更好发挥水库综合效益的方案。本文提出的面向双保证率水库供水能力优化计算方法，满足多个保证率要求对水库调度规则和供水能力进行同步优化，可以实现多目标、多保证率的水库供水能力计算。通过对赤田水库的实例研究验证，结果表明：（1）算法具有较好的收敛性，可以满足不同保证率目标下的调度线和供水能力优化计算，生成的调度线年内分布合理，与来水和需水过程等影响因素相符合；（2）随着农业保证率提高，水库总供水能力和城镇供水能力均呈下降趋势，而总供水量先增加后减少。当农业保证率超过50%后城镇供水量下降幅度加大，说明满足枯水年份农业需水会对城镇供水产生较大影响；（3）受农业需水的年际、年内变化过程影响，在农业供水量相近的情况下，提高农业保证率对城镇供水能力的不利影响高于增加农业需水。

考虑实际工作需求，还可进一步研究考虑调度效益、农业需水过程变化等影响因素下的供水能力和调度规则优化，以及不同工程、用户组合下的供水系统供水能力计算，使计算方法具有更强的实用性和通用性。