考虑聚羧酸减水剂作用的水泥净浆水膜厚度模型

2022-06-28辛全浩梁云涛

建筑材料学报 2022年5期

郑丹，辛全浩，梁云涛

（重庆交通大学河海学院，重庆 400074）

水泥浆体的工作性能是混凝土配合比设计的关键因素，也直接影响硬化混凝土的强度和耐久性.混凝土的工作性能受用水量、颗粒级配、颗粒形状及减水剂等众多因素影响［1］，目前尚没有理论模型可以准确、定量地计算拌和物的工作性能，在实际工程中主要依靠经验和试拌来获得合适的混凝土配比.高性能混凝土对拌和物的要求更高，骨料变化特别是机制砂的广泛应用，给试配工作带来更多不确定因素，急需从理论上指导水泥基材料的配合比设计［2］.从20世纪50 年代开始，研究人员采用流变学理论中的Bingham 模型［3］来分析水泥浆体的工作性能.但是，Hafid 等［4］发现水泥浆的流变曲线实际上非线性，特别是在减水剂掺入后体现出明显的剪切增稠效应，Bingham 模型不一定适用［5］.于是研究人员采用更为复杂的修正Bingham 模型和Herschel‑Bulkley 模型来描述水泥浆体的工作性能［6］.但是，目前水泥基材料流变特性参数的测试技术并不完善［7］，流变参数并不能很好地反映拌和物的工作性能，完全从理论上研究水泥浆体的工作性能和指导混凝土配合设计还存在很多困难.

堆积密实度［8］是反映固体颗粒体系的一个重要参数，较高的堆积密实度也是水泥基材料获得高工作性能的关键.从20 世纪30 年代起，Furnas［8］开始研究球形颗粒的堆积理论，而Powers［9］提出了考虑松动效应的堆积模型，Stovall 等［10］提出了“线性堆积密度模型”，De Larrad［11］提出了“可压缩堆积模型”等，但这些理论模型简化假设和计算参数较多，计算结果与实际情况存在一定的差异［12］.在总结现有堆积密实度测量方法的基础上，Wong 等［12］采用湿测法测量实际工作状态下的颗粒堆积密实度，并提出了水膜厚度理论［13‑14］，认为填充固体空隙所需后的富余水，将以涂覆颗粒表面水膜的形式存在，水膜厚度越高，拌和物的流动性越好.研究表明，该模型能较好地反映不同骨料级配、不同掺合料、不同纤维掺量的水泥浆体工作性能［15‑17］，但模型并没有考虑到减水剂的影响，不同减水剂掺量下的水膜厚度不能直接比较，给科学指导配合比设计带来一定困难.肖佳等［18］采用水膜厚度理论分析了水泥-石灰石粉浆的流变特性.现有研究表明［19］，减水剂的作用机理主要是通过分散固体颗粒，一定程度地释放水泥颗粒间的絮凝水，为拌和物提供更多的富余水量，从而提高混凝土的工作性能［20］.曹恩祥等［21］分析了减水剂对新拌水泥浆微结构的影响规律；吴琼［22］采用激光粒度仪分析了粉体材料中絮凝水的释放过程.但如何定量分析减水剂对絮凝水的影响规律，并指导混凝土配合比设计，一直是研究中尚未解决的问题.

本文进行水泥颗粒的堆积密实度和水泥净浆的工作性能试验，分析减水剂对颗粒材料絮凝水的影响规律，计算不同减水剂掺量下的絮凝水释放量，据此提出考虑减水剂作用的修正水膜厚度模型，并与已有的试验结果进行对比.

1 试验

1.1 原材料

水泥选用产自重庆小南海水泥厂的P·O 42.5普通硅酸盐水泥，其比表面积为367.08 m2/kg，密度为3.1 g/cm3，化学组成见表1.水泥性能符合GB 175—2007/XG1-2009《通用硅酸盐水泥》.聚羧酸减水剂为固含量（质量分数，文中涉及的含量、掺量、水灰比等除特别说明外均为质量分数或质量比）98%的水溶性粉剂.

表1 水泥的化学组成Table 1 Chemical composition of cement w/%

1.2 堆积密实度测试

堆积密实度φ的定义为固体颗粒体积与总堆积体积的比值.采用湿测法测量减水剂掺量（ω）为0%、0.10%、0.20%、0.40%的拌和物堆积密实度.为确定最佳水固比（uw，水与固体颗粒的体积比），第1 次试验从uw=1.2 开始，然后依次降低水固比，直到固体浓度达到最大值，开始下降后停止.

湿测法的具体操作流程如下［12］：首先，设定水固比，称取所需质量的水、胶凝材料和减水剂，预混2 min 后加入搅拌容器中，再将一半胶凝材料和减水剂加入搅拌容器中低速搅拌3 min；然后，将剩余胶凝材料和减水剂分成4 等份，依次加入搅拌容器中低速搅拌3 min；最后，用拌和物填充体积为300 mL 的圆柱形模具，根据需要进行振动，再用尺子抹去多余部分并称量模具中浆体的质量.重复上述步骤，即可获得不同水固比下拌和物的堆积密实度.

1.3 净浆流动性测试

根据GB/T 8077—2012《混凝土外加剂匀质性试验方法》，水泥净浆流动性主要通过扩展度来反映，本试验采用上口直径70 mm、下口直径100 mm、高度60 mm 的截锥圆模.提起圆模后，水泥净浆在玻璃板上自由流动30 s，测量流淌部分相互垂直2 个方向的最大直径，取其平均值为扩展度.试验中水灰比从0.20 到0.40 变化（以0.05 为级差），为便于比较，表2 中质量比统一转换为体积比表示，固定浆体体积为1 200 mL.减水剂掺量为0.10%、0.15%、0.20%、0.25%、0.30%、0.40%.试验共配制27 组水泥净浆配比，以“水固比-减水剂掺量”（括号里的数据为对应的质量比）为编号，试验配合比及水泥净浆扩展度见表2.

表2 试验配合比及水泥净浆扩展度Table 2 Mix proportions and flow spreads of cement pastes

2 结果与分析

2.1 空隙比与水固比

试验水泥净浆中不含其他胶凝材料，因此水泥颗粒体积Vc可以表示为：

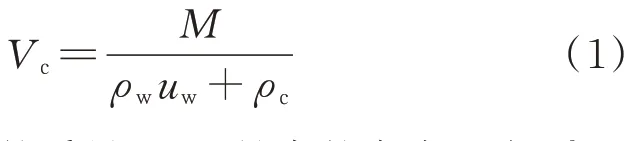
式中：M是拌和物的质量，g；ρw是水的密度，g/cm3；ρc是水泥的密度，g/cm3.

根据堆积密实度试验结果，可将堆积密实度φ和空隙比（u，空隙与总颗粒材料的体积比）表示为：

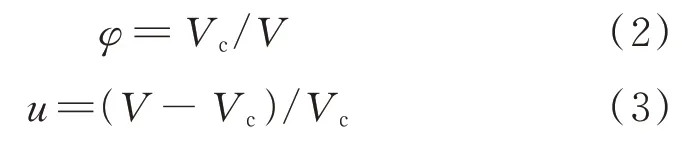
式中：Vc为总颗粒材料的体积，mL；V为总堆积体的体积，mL.

不同减水剂掺量下的空隙比u与水固比uw的关系如图1 所示.

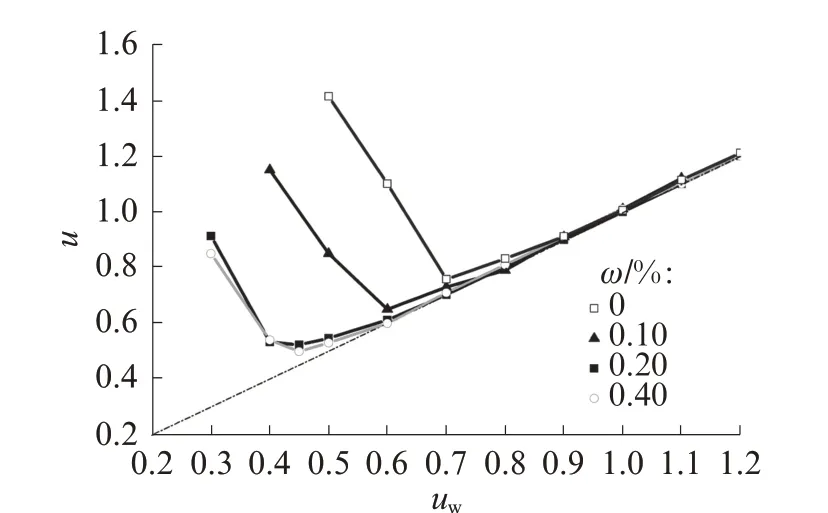
图1 不同减水剂掺量下空隙比与水固比的关系Fig.1 Relationship between u and uw with different superplasticizer contents

由图1 可见：随着水固比的增加，拌和物的空隙比先减少后增加.这是因为颗粒间存在范德华力和电双层力等表面力，导致颗粒发生聚集.随着拌和水的加入，颗粒的亲水性导致相互作用的表面力被水破坏，团聚颗粒分离，空隙比减小.当拌和水超过一定程度后，多余的水分并不能起到分离颗粒的作用，空隙率随之增加［12］.因此湿测法和水膜理论认为空隙比最低时即对应于最佳堆积密实度［13］，后续水分可以作为自由水形成水膜，提供拌和物的流动性能.

式中：WFT 为水膜厚度，μm；umin为最小空隙比；A为骨料比表面积，m2/kg.但式（4）没有考虑减水剂对絮凝水的释放作用，导致水膜厚度计算的结果存在误差，因此需要修正.从图1 还可以看出，在相同水量下，掺减水剂拌和物的空隙率明显减少.这是由于静电等作用会使得液体和颗粒之间的结合更加紧密，引发絮凝，导致部分水分被包裹而未参与对水泥颗粒的分散作用；加入减水剂后，表面活性剂将有效地改变颗粒和液体间的表面作用力，絮凝水释放，团聚颗粒堆积更加密实.为进一步分析颗粒材料掺入水分后颗粒空隙的变化规律，可以将水固比uw与空隙比u的关系绘制成图，如图2 所示.

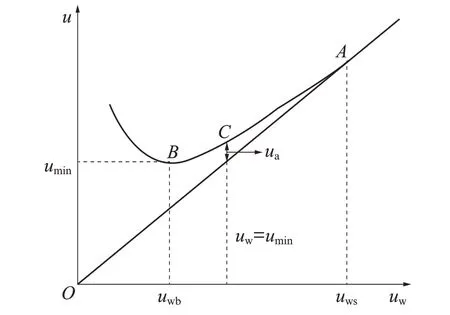
图2 水固比与空隙比的关系示意图Fig.2 Schematic diagram of water solid ratio and void ratio

由图2 可见：拌和物的空隙比曲线一直高于直线OA，拌和物的空隙始终高于加入水的含量，直到A点二者相切.因此颗粒堆积材料的空隙可以分为2 部分，一部分是掺入水固比uw，另一部分是颗粒体剩余空隙ua.

当掺入与umin相等的水量时（C点），此时ua＞0，这意味着仍然有部分空隙没有完全填充密实.直到A点ua=0，此时空隙被填满，浆体达到饱和状态，后续增加的水分完全作为“富余水”.因此本文定义最低点B对应的最小空隙比为最小水比uwmin，最低点对应的水固比为基本水比uwb，该曲线与uw=u直线的切点A（ua=0）为饱和水比uws.不同减水剂掺量下的uwmin、uwb、uws如表3 所示.

表3 最小水比、基本水比、饱和水比Table 3 Minimum water ratio，basic water ratio and saturated water ratio

从表3 可以看出，随着减水剂掺量的增加，饱和水比、基本水比以及最小水比均减少.这是因为被絮凝体包裹的自由水分没有直接参与水泥基颗粒材料间的分散和润滑，掺入减水剂后，由于显著的分散作用，在使颗粒堆积更为紧密的同时能够释放絮凝水，从而表现为最小水比、基本水比、饱和水比均伴随减水剂掺量的增加而持续降低.

本文在研究减水剂对絮凝水的释放作用时，还考虑了振动对空隙比的影响，结果如图3 所示.由图3 可见：加入减水剂后，由于减水剂的空间位阻作用，导致颗粒聚集体打开，絮凝水得到释放，颗粒表面充分吸附富余水，基本水比和饱和水比均得以减小；在振动情况下，由于颗粒更加密实，因此基本水比和最小空隙比均减小，但是饱和水比基本保持不变.

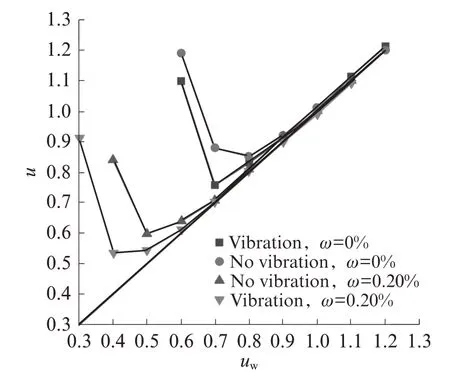
图3 振动对空隙比的影响Fig.3 Effect of vibration on void ratio

2.2 减水剂与絮凝水释放

从图1、3 可以看出，当水固比超过饱和水比后，颗粒和絮凝体之间的空隙均被水填满，此时可以认为材料为饱和状态，后续水分便成为富余水.因此，忽略水泥水化作用时，拌和物内的水分可分成3 部分：填补空隙水分（其值等于umin）、絮凝水和提供流动性和水膜的水分uwf.当掺入水分超过饱和水比后，后续外加水分均提供混凝土流动性，不再有多余絮凝水产生，可以认为：

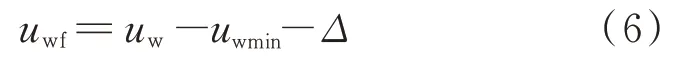
式中：Δ为饱和水比下的絮凝水比.对比不同减水剂掺量下的饱和水比，由于后续掺入水分都为“富余水”，提供拌和物的流动性，不再有新的絮凝水产生，可以认为在饱和水比状态下，不掺减水剂和掺减水剂的饱和水比差值即为对应的絮凝水释放量δ，因此不同减水剂掺量下的絮凝水比为：

式中：Δ0为不掺减水剂时拌和物在饱和水比下的絮凝水比.

根据表3 中的饱和水比，可以求得不同减水剂掺量下的絮凝水释放量δ，如图4 所示.

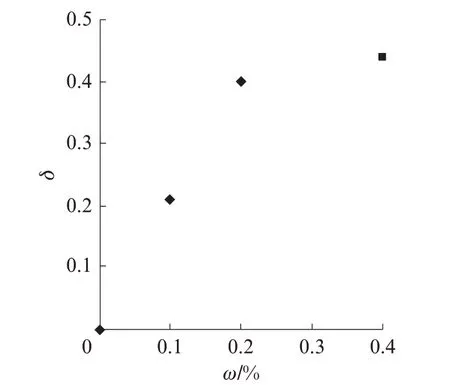
图4 减水剂掺量和絮凝水释放量的关系Fig.4 Relationship between superplasticizer contents and flocculating water releases

由图4 可见：减水剂掺量为0%～0.20%时，絮凝水的释放量和减水剂掺量成正比；当减水剂掺量超过一定值后，减水剂产生的空间位阻作用基本完成，饱和水比变化不再明显，后续添加的减水剂对絮凝水释放作用减小，所以絮凝水的释放量偏小.当缺少饱和水比数据且减水剂掺量在规定范围时，可以假设絮凝水释放量为：

式中：k为絮凝水释放系数，需通过试验率定.

需要指出的是，减水剂掺量超过一定值后（本文为0.40%），絮凝水释放效率降低，这是因为絮凝水有限，过量的减水剂并不能提供多余水量.考虑减水剂作用后，修正水膜厚度RWFT 可以表示为：

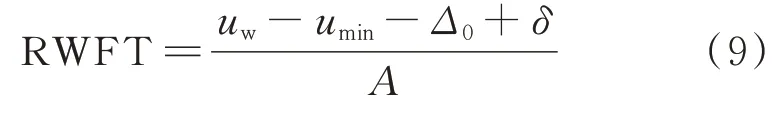
从图1 和式（9）不难看出，减水剂在拌和物中的作用实际上同时体现在2 个方面：一方面是絮凝水的释放，使得更多的水分参与包裹、润滑胶凝材料颗粒，提供拌和物的流动性，这点主要体现在湿测法中不同减水剂掺量下饱和水比的差别上；另一方面是将胶凝材料团聚颗粒充分分散，使得颗粒充分密实，增大拌和物的堆积密实度，这点主要体现在湿测法中不同减水剂掺量下最小空隙比的差别上.

2.3 拌和物工作性能

从表2 可以看出，随着减水剂掺量和用水量的增加，拌和物扩展度增加.下面分别采用Kwan等［13］提出的水膜厚度模型和本文提出的修正水膜厚度模型，计算不同水固比-减水剂掺量下的水膜厚度.为了更直观地反映水膜厚度对净浆流变性能的影响，本文采用相对扩展度（R）与水膜厚度进行比较，其计算公式如下：

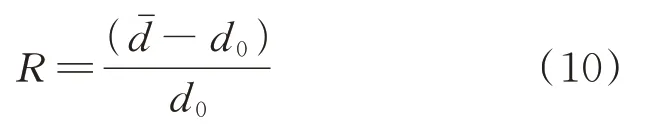
式中：d0和分别为坍落扩展度筒的底面直径和净浆扩展度，mm.在本文计算中，水泥颗粒的比表面积为1 137 948 m2/m3.未进行湿测法测试的减水剂掺量试验组，饱和水比和絮凝水释放量采用线性插值得到.从图1 可以看出，减水剂掺量为0.40%时，饱和水比和基本水比保持不变，可以认为此时不存在絮凝水，即Δ=Δ0-δ=0，因此本文计算中取Δ0为减水剂掺量为0.40%的絮凝水释放值（δ=0.44）.

图5为不考虑减水剂作用时的水膜厚度与相对扩展度的关系.图6 为考虑减水剂作用的修正水膜厚度与相对扩展度的关系.由图5、6可见：在单一减水剂掺量下，水泥净浆扩展度与原水膜厚度具有良好的相关性，但减水剂掺量对拌和物的工作性能影响较大，不同减水剂掺量下的拌和物工作性能不能直接比较；考虑颗粒絮凝和减水剂作用后，本文提出的修正水膜厚度模型与拌和物的工作性能呈现良好的线性关系，可以较好地指导混凝土配合比设计.需要说明的是，即使减水剂掺量较大，拌和物中仍然会有少量絮凝水，实际上Δ0要高于0.44，但从图中可以看出Δ0仅对拟合直线起平移作用，不影响拟合精度，也不影响通过拟合直线确定已知水膜厚度下拌和物的扩展度.另外，由式（6）可见，当掺入水分小于饱和水比时，絮凝水的释放量小于Δ0，按式（9）计算得到的水膜厚度偏小，此时的修正水膜厚度为负值.

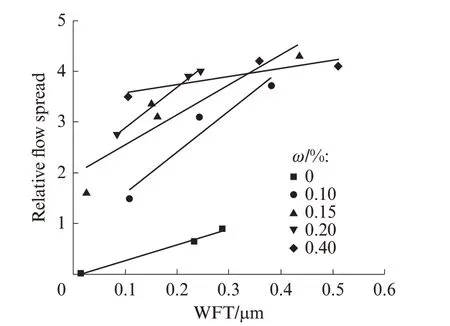
图5 不考虑减水剂作用的水膜厚度与相对扩展度的关系Fig.5 Relationship between WFT and relative flow spread without considering superplasticizer

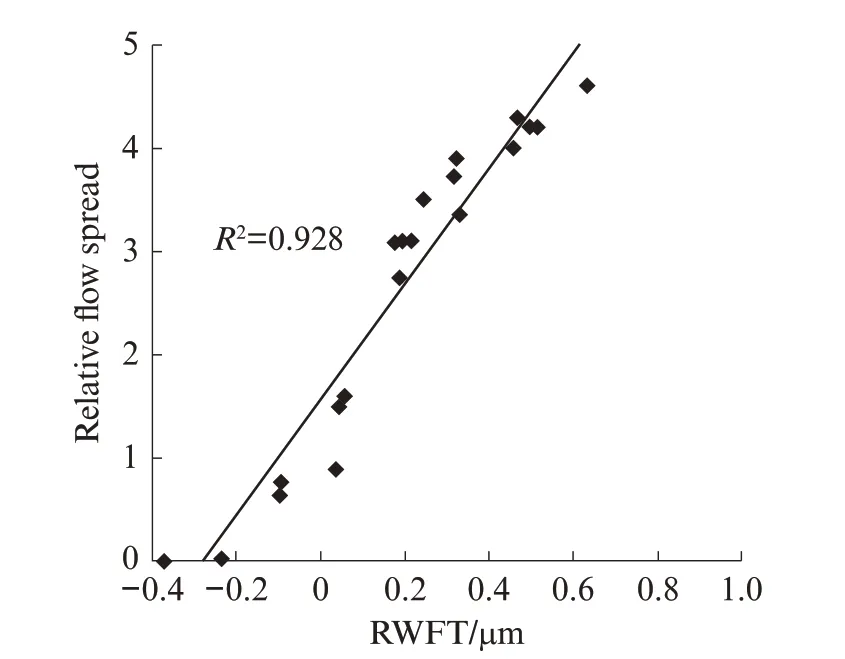
图6 考虑减水剂作用的修正水膜厚度与相对扩展度的关系Fig.6 Relationship between RWFT and relative flow spread with considering effect of superplasticizer

3 讨论

为进一步检验本文提出的修正水膜厚度模型的合理性，采用文献［15］中的试验数据进行对比，结果如图7、8 所示（图中没有展示扩展度为0 的数据）.由图7、8 可见：在单一减水剂掺量条件下，水泥净浆扩展度与水膜厚度具有良好的相关性，但当减水剂掺量变化时，拌和物工作性能差别较大；由于文献［15］中仅测量了湿测法的空隙率最低点，无法确定不同减水剂掺量下的絮凝水释放量，絮凝水释放量计算中按式（8）进行拟合，得到絮凝水释放系数k=5，同样根据修正的水膜厚度模型，可以看出水膜厚度与相对扩展度有良好的相关性.

图7 水膜厚度与相对扩展度的关系Fig.7 Relationship between WFT and relative flow spread

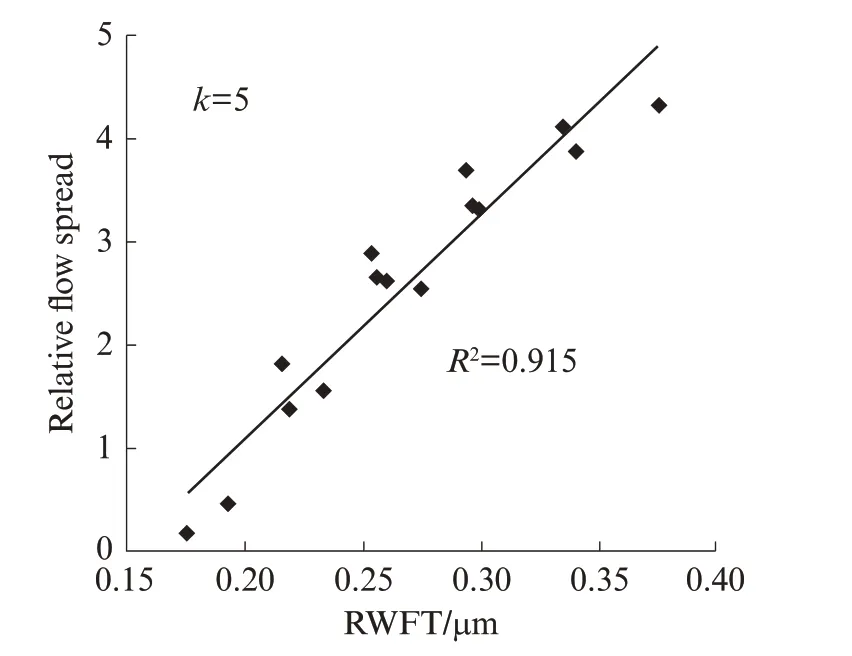
图8 修正水膜厚度与相对扩展度的关系Fig.8 Relationship between RWFT and relative flow spread

文献［15］还对水泥中加入20%粉煤灰、20%硅灰+20%粉煤灰的胶凝材料进行了工作性能试验.本文采用上述方法对其浆体扩展度和修正水膜厚度进行了拟合，结果如图9 所示.由图9 可见：模型与试验结果吻合良好；在不同掺合料情况下，絮凝水释放系数分别为k=3和k=5，这说明本文提出的模型可以分析不同掺合料、不同减水剂掺量下水泥浆体的工作性能.