圆形连接器的对流换热系数

林雪燕， 张元培

(北京邮电大学电连接与可靠性科研室，北京海淀区，100876)

1 引言

连接器在工作时通以电流产生的热量，使连接器的各部件的温度升高，当温升过高时就会影响连接器的电气性能、机械性能以及工作可靠性，甚至可能会发生故障。对连接器进行热设计和热分析已经成为了不可或缺的研究内容。

电流通过电连接器接触件时，由于接触件的体电阻和插针-插孔间的接触电阻，产生的焦耳热是引起电连接器温升的主要热源。在连接器内部，热量只考虑接触件和绝缘体的导热方式传递至外壳。在连接器外部，通过对流和辐射方式的共同作用将传递至外壳的热量向周围环境散失。有限元仿真被广泛用于连接器热性能的分析与设计，为了获得准确的结果，关键问题之一是对流换热系数确定与获取。

自然对流换热系数的计算非常繁琐，影响因素众多，流体的物理性质、换热表面的形状、换热的部位、以及流体的流速等都对对流换热过程有影响。对流换热系数通常使用经验值，如连接器在室温下的大气环境中工作时，空气的自然对流换热系数为5 ～ 25 W/(m2·℃)[1]，而室内无风环境下的自然对流换热系数在4～5 W/(m2·℃)左右[2]。对流换热系数是产生仿真结果不准确的一个原因，根据量纲法和迭代法可精确计算对流换热系数。吴珊珊[3]编写MATLAB程序进行对流换热系数的计算，并得到某款电动汽车连接器在环境温度为25℃，额定电流250A，只考虑接触件体电阻生热的情况下，空气自然对流换热系数为12.8 W/(m2·℃)。程宇和张巨伟[4]采用ANSYS软件进行结构热分析，提出一种精确确定管道外自然对流换热系数的迭代方法，得出空气的换热系数一般在 1～10 W/(m2·℃)之间；当环境温度为-27 ℃时，空气对流换热系数为 4.67 W/(m2·℃)；环境温度为39.5 ℃时，空气对流换热系数为3.68W/(m2·℃)；对流换热系数随温度的升高而降低。陈孟等[5]利用自然对流换热实验关联式和ANSYS软件的结构稳态热分析，通过APDL语言编程进行迭代计算，从而求得自然对流换热系数；空气的自然对流换热系数一般在 1～10 W/(m2·℃)之间，水的自然对流换热系数一般在 200～1000 W/(m2·℃)之间。胡彩莲[6]基于利用ANSYS Workbench软件中的热-电耦合模块和MATLAB程序对连接器的综合散热系数进行了迭代计算，得出在不同低温工况下，综合散热系数值的差别很大，但变化不超过0.05 W/(m2·℃)。

本文基于MATLAB GUI软件对圆形连接器的对流换热系数计算进行了界面设计。只需在GUI界面上输入电流、接触件的芯数、电阻率和半径、外壳长度、特征尺寸以及外界环境温度，就可得到该条件下准确的对流换热系数。同时，本文对连接器的放置方式、特征尺寸、外界环境温度、电流和芯数对对流换热系数的影响进行了分析。

2 迭代法计算圆形连接器对流换热系数

连接器的热路图如图1所示。电流I流过电阻为R的接触件时，会产生焦耳热I2R，从而使导体温度升高为Tc。该热量依次通过绝缘体导热(热阻为Rλ1)和外壳导热(热阻为Rλ2)，将热量传递至外壳表面，使温度升高为Tw。传递至外壳的热量再通过空气的自然对流换热(热阻为Rc)和辐射换热(热阻为Rr)传递至温度为T0的外界环境中。

图1 连接器的热路图

热流方程为：

(1)

圆形连接器绝缘体和外壳都是圆筒壁，导热热阻Rλ为：

(2)

式(2)中，λ为材料的导热系数；L为长度；d2为外径；d1为内径。

由牛顿冷却方程计算对流换热的热流量：

qc：qc=hcAc(Tw-T0)

(3)

自然对流换热的热阻Rc为：

(4)

式(3)和(4)中，hc为对流换热系数W/(m2·K)；Ac为对流换热面积(m2)，圆柱体的对流换热面积为其外表面积。

由四次方定律计算辐射换热的热流量qf：

(5)

辐射换热的热阻为Rf：

(6)

式(5)和式(6)中，ε为物体的黑度；Af为辐射表面积(m2)，对于圆柱体Af=Ac； 0为斯蒂芬-玻尔兹曼常数(=5.67×108W/(m2·K4))。

连接器的辐射换热能力通常远小于对流换热能力，所以本文不考虑连接器外壳的辐射换热。此时，热平衡方程为：

(7)

对流换热系数hc为：

(8)

式(8)中，Nu为努赛尔数；λf为空气的热导率(W/(m·K))；D为散热体的特征尺寸(m)，圆柱体水平放置时的特征尺寸为直径，竖直放置时的特征尺寸为高度；Gr为格拉晓夫数；Pr为普朗特数；g为重力加速度(m/s2)；αv为空气的膨胀系数(K-1)；v为空气运动粘度(m2/s)；下角标m表示定性温度，为(Tw+T0)/2；C和n是依据Gr×Pr进行取值[7-8]。

由式(8)可知，为了计算对流换热系数hc，必须先知道连接器外壳温度Tw。为了解决这个僵局，需先假设一个温升ΔT=Tw-T0，再由图2所示的迭代过程计算hc值，直到ΔT的计算结果与初始设定值之间的偏差足够小，迭代计算完成。本文取初始温升ΔT为30K，取小偏差的阈值为0.1，对流换热系数为0说明不需考虑自然对流换热效应。由于计算对流换热系数的过程比较繁琐，所以本文编写了MATLAB计算程序并设计相应的GUI界面来实现这一迭代过程。

图2 对流换热系数的迭代计算流程图

3 MATLAB编程及GUI界面设计过程

3.1 编写MATLAB函数

本文创建了[dt, hc] = thermal_horizontal(T0, D, I, p, r, L,S)和[dt, hc]= thermal_vertical(T0, D, I, p, r, R,S) 函数分别来计算圆形连接器水平放置和竖直放置时的空气对流换热系数。这两个函数的输入参数包括环境温度T0、特征尺寸D、电流I、接触件的电阻率 、半径r和芯数S、连接器外壳长度L和半径R。圆形连接器水平放置时的特征尺寸D等于外壳直径(2R)，竖直放置时的特征尺寸D等于外壳长度L。这两个函数的输出参数为对流换热系数hc和连接器外壳表面温升dt。

3.2 GUI界面设计

圆形连接器对流换热系数的MATLAB GUI界面由二级界面组成。其中，一级界面说明功能和连接器的放置方式，二级界面分别完成连接器不同放置方式时的计算窗口。界面设计在MATLAB App Designer工具中进行，设计完成的一级界面和二级界面如图3所示。

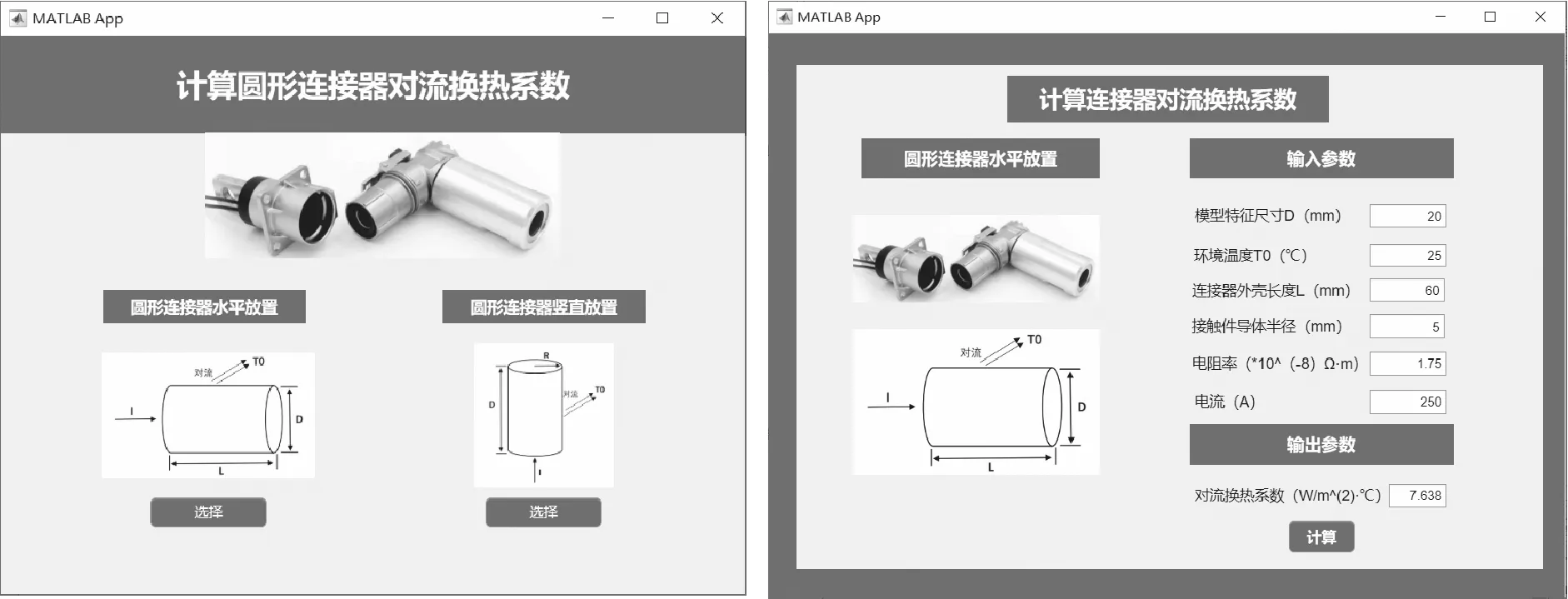
(左：一级界面图，右：圆形连接器水平放置时二级界面图)

一级界面设计由标签、图像和按钮三种组件组成。标签包含标题 “计算圆形连接器对流换热系数” 和放置方式描述“圆形连接器水平放置”和“圆形连接器竖直放置”。图像区域放置了“圆形连接器”、 “水平放置的简化圆形连接器”和“竖直放置的简化圆形连接器”三个图片。两个“选择”按钮进入二级界面图。右击“选择”，在出现的快捷菜单上选择“回调”和“转至ButtonPushed回调”，此时自动进入“代码视图”中按钮对应的回调函数代码处，输入“run hc_horizontal.mlapp”和“run hc_vertical.mlapp”(二级界面的文件名)语句以调用二级界面对应的文件。最后点击保存，就完成了一级界面的设计。

二级界面设计由标签、图像、编辑字段(数值)和按钮四种组件组成。从组件库中选择七个编辑字段(数值)组件添加到设计视图中，分别添加文字“模型特征尺寸D(mm)”、“环境温度T0(℃)”、“连接器外壳长度L(mm)”、“接触件导体半径(mm)”、“电阻率(*10^(-8)Ω·m)”、“芯数S”、“电流(A)”和“对流换热系数(W/m^(2)·K)”。在右上角的“组件浏览器”中通过双击将各组件分别重新命名为app.size、app.temperature、app.Lmm、app.radius、app. resistivity、app.number 、app. Current和app. Coefficient。“计算”为按钮组件，进入其代码视图中出现的空白区域中，输入以下语句为各参数赋值：

T0 = app.temperature.Value; %为环境温度T0 (℃) 赋值

D = app.size.Value; %为连接器特征尺寸D(mm) 赋值

I = app.current.Value; %为连接器通以的电流I (A) 赋值

p = app.resistivity.Value; %为连接器接触件的电阻率p(*10^(-8)Ω·m)赋值

r = app.radius.Value; %为连接器接触件导体半径r(mm)赋值

L = app.Lmm.Value; %为连接器外壳长度L(mm)赋值

S = app.number.Value; %为连接器芯数S赋值

[～,hc] = thermal_horizontal(T0,D,I,p,r,L); %连接器水平放置时的对流换热系数计算

app.coefficient.Value = hc; %将对流换热系数计算结果赋值给输出组件

图3的右图给出了当外壳直径为20mm，长度为60mm，接触件(芯数为1)导体半径为5mm，导体材料为Cu(电阻率为1.75×10-8Ω·m)的圆形连接器水平放置于温度为25℃的空气中，通以电流为250A时，自然对流换热系数为8.27W/(m2·K)。

4 对流换热系数的影响因素

4.1 特征尺寸的影响

图4为圆形连接器特征尺寸D对空气对流换热系数hc的影响曲线。随着特征尺寸D的增加，连接器的自然对流换热系数hc减少，满足如式(9)和式(10)所示的幂函数关系，其中R2为拟合的可靠度。圆形连接器水平放置时，当外壳直径小于17mm，则无须考虑对流换热。竖直放置时，当外壳长度小于18mm，则无须考虑对流换热。以外壳直径为20mm、长度为60mm的连接器为例，水平放置时的hc为8.27 W/(m2·K)，竖直放置时为7.23 W/(m2·K)。在实际应用中，为了增加对流换热而降低连接器温升，建议将其水平放置。

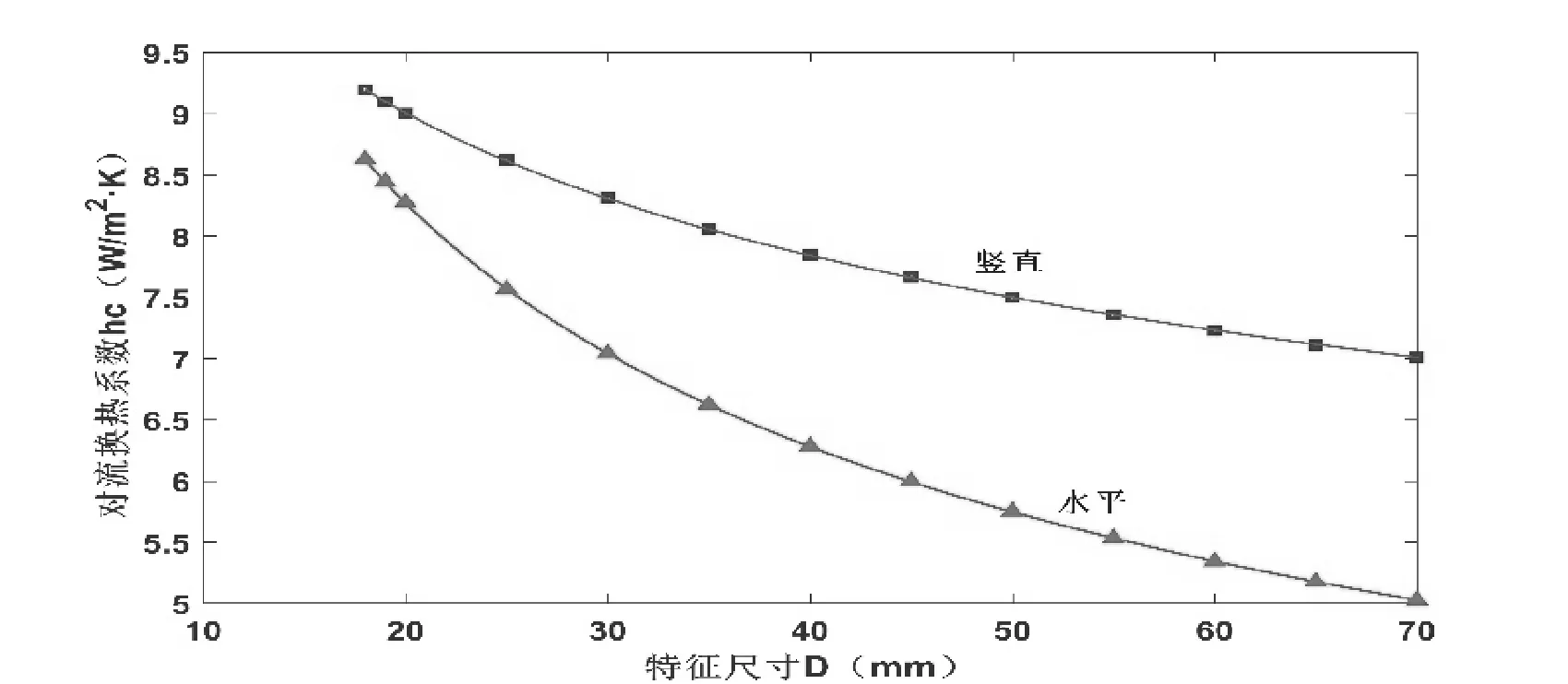
(条件：I=250A，r=5mm，S=1，L=60mm，

hc水平=27.21D-0.40(D≥17mm,R2=1)

(9)

hc竖直=16.39D-0.20(D≥18mm,R2=1)

(10)

4.2 环境温度的影响

图5为环境温度T0对空气对流换热系数hc的影响曲线。随着环境温度T0的增加，连接器的自然对流换热系数hc减少，满足如式(11)和式(12)所示的二项指数函数的线性叠加关系。当T0为相同值时，圆形连接器水平放置时的hc大于竖直放置时，即圆形连接器水平放置时的自然对流换热要大于竖直放置时。水平放置时，当环境温度超过62.5℃，则无须考虑对流换热。

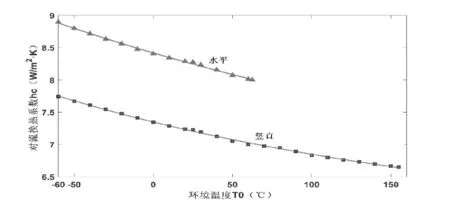
(条件：I=250A，r=5mm，S=1，R=10mm、L=60mm)

hc水平=0.0014e-0.06T0+8.42e-0.0008T0(T0≤62.5℃,R2=0.9985)

(11)

hc竖直=0.15e-0.0002T0+7.20e-0.001T0(R2=0.9992)

(12)

4.3 电流的影响

图6为电流I对空气对流换热系数hc的影响曲线。随着电流I的增加，连接器的自然对流换热系数hc增加，满足如式(13)和式(14)所示的幂函数关系。当电流I为相同值时，圆形连接器水平放置时的hc大于竖直放置时的hc。圆形连接器水平放置时，当电流I小于191A时，则无须考虑对流换热。竖直放置时，当电流I小于32A时，则无须考虑对流换热。

(条件：r=5mm，S=1， R=10mm，L=60mm，T0=25 C)

hc水平=0.97I0.39(I≥191A,R2=0.9997)

(13)

hc竖直=0.82I0.39(I≥32A，R2=0。9998)

(14)

4.4 芯数的影响

图7为芯数S对空气对流换热系数hc的影响曲线。随着芯数S的增加，连接器的自然对流换热系数hc减少，满足如式(15)和式(16)所示的幂函数关系。当S为相同值时，圆形连接器水平放置时的hc大于竖直放置时，即圆形连接器水平放置时的自然对流换热要大于竖直放置时。

(条件：I=250A，r=1.5mm，R=10mm，L=60mm，T0=25 C)

hc水平=12.65S-0.17(R2=0.9993)

(15)

hc竖直=10.99S-0.17(R2=0.9990)

(16)

5 总结

本文以圆形连接器为研究对象，基于热路图、热平衡方程和迭代法，开发了MATLAB GUI界面软件来快速而准确计算自然对流换热系数，为ANSYS准确分析连接器的热性能提供必需的参数。自然对流换热系数随着特征尺寸的增大而呈幂函数减少，当水平放置的圆形连接器外壳直径小于17mm，当竖直放置的圆形连接器外壳长度小于18mm，均可忽略对流换热对温升的影响。自然对流换热系数随着环境温度的升高而呈指数函数减少，当圆形连接器水平放置于温度低于63 C的大气环境中时，可忽略对流换热对温升的影响。自然对流换热系数随着电流的增大而呈幂函数增加，当水平放置的圆形连接器通以的电流小于191A，当竖直放置的圆形连接器通以的电流小于32A时，均可忽略对流换热对温升的影响。自然对流换热系数随着芯数的增加而呈幂函数减少。实际应用时，为了增加对流换热效应和减少连接器温升，建议将圆形连接器水平放置。后续将开发计算矩形连接器对流换热系数的MATLAB GUI界面。