弯曲钢梁正应力和挠度的试验与数值模拟*
2022-06-28姚子谦谢梓郁
陈 锴,姚子谦,谢梓郁,陈 丽
(1.福州大学 至诚学院 环境资源工程系,福建 福州 350002;2.福州大学 至诚学院 材料工程系,福建 福州 350002)
在实际工程问题中,有很多杆件是承受弯曲变形的,为保证弯曲构件正常工作,不但要求构件有足够的强度,还要求有足够的刚度。例如,桥式起重机梁在起吊重物后若其弯曲变形过大,会使小车行走困难,出现爬坡现象;汽车轮轴上的叠板弹簧是利用其弯曲变形来缓和车辆受到的冲击和振动,这时要求弹簧有较大的变形[1],因此为了限制或利用弯曲构件的变形,并满足正常使用极限状态的要求,应研究构件的弯曲变形规律,合理计算使用载荷下构件的应力和挠度[2-4]。
目前,许多学者基于弹性力学的方法对各类梁发生纯弯曲时的变形规律进行了理论分析与计算,但通过理论分析、实验验证和模拟仿真三者相结合的方式对梁发生纯弯曲和横力弯曲时变形规律的研究相对较少,实验结合模拟计算是目前科学研究的重要方法[5-8],因此本文使用多功能组合实验装置和静态数字应变仪对矩形截面梁在弹性范围内进行纯弯曲试验,测定沿其横截面高度的正应变分布规律,进一步对截面上应力分布规律进行研究。同时应用ANSYS有限元软件对3种截面梁的弯曲过程进行有限元仿真模拟[9-11],采用理论推导法、实验法和有限元模拟法三者相结合的方式,验证仿真模拟结果的准确性;采用模拟仿真法计算不同截面梁发生弯曲时的正应力和挠度,其结果能为实际工程的应用提供有意义的参考。
1 纯弯曲梁试验方法
试验使用多功能组合实验装置和静态数字应变仪(见图1),采用螺旋推进和机械加载方法。当增加压力ΔP时,梁的受力点处分别增加作用力ΔP/2。梁材料弹性模量E=210 GPa,泊松比μ=0.28,跨度L=370 mm,横截面尺寸c=15 mm,h=25 mm,a=125 mm,简支梁如图2所示;为了测量梁纯弯曲时横截面上的应变分布规律,在梁纯弯曲段侧面各点沿横截面高度方向布置5片应变片,3#在h/2处,2#和4#在上下对称于3#的h/4处,1#和5#在梁的上下表面(见图2)。

图1 纯弯曲梁实验装置

图2 梁上应变片的分布位置
2 试验和理论结果分析
2.1 正应力
试验时采用等量逐级加载,增加压力ΔP=300 N,Pmax=2 100 N,每增加ΔP,测得梁沿高度各点处的轴向应变,由单向应力状态胡克定律公式σ=E·ε,求得各点处应力试验值。
2.2 挠度
根据材料力学理论可知,当图1所示简支梁AB上只有一个载荷F作用时,利用积分法可得梁挠曲线方程:
当0≤x≤a时,
(1)
当a≤x≤L时,
(2)
式中,b=L-a;w为挠度值;x为梁上任一点至A端的水平距离。图1所示简支梁AB在2个载荷ΔP/2作用下,梁挠曲线方程可利用叠加法求得。
2.3 结果分析
矩形截面梁纯弯曲段各测点正应力增量的实测值与理论值见表1。
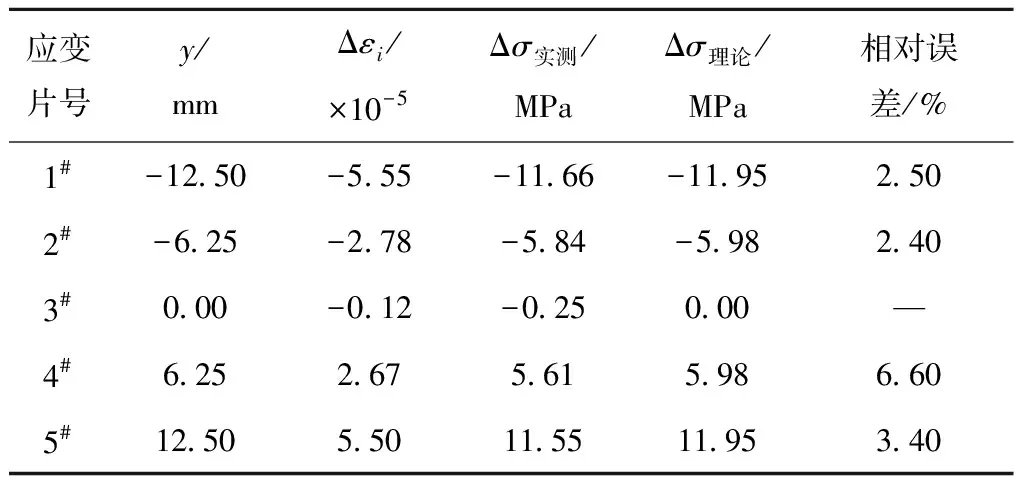
表1 矩形截面梁上5个测点处的正应力值
由表1可知,3#应变片位于中性层,其正应力几乎为零;1#和2#应变片位于梁中性层上侧,应力值为负,即梁中性层之上部分受挤压;4#和5#应变片位于梁中性层下侧,正应力为正,即梁中性层之下部分受拉伸。正应力沿梁高度几乎呈线性分布,越靠近梁的上下边缘应力值越大。应力实测值与理论值十分相近,但存在一定误差,这主要与试验精度有关,仪表越精确,其值越准确,相对误差越小。
3 仿真模拟与分析
3.1 纯弯曲
在ANSYS有限元软件界面上,按矩形截面梁的实际尺寸建立三维模型并进行有限元模拟分析;图3所示给出了梁在载荷作用下,其纵向正应力的分布情况。
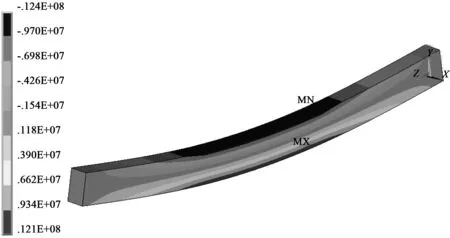
图3 矩形截面梁的弯曲正应力分布图
由图3可知,纵向正应力在梁中性层处为零,在梁中性层上方纵向纤维受挤压,中性层下方纵向纤维受拉伸;应用ANSYS软件的通用后处理器读取梁上5个测试点的应力增量值,具体见表2。

表2 纯弯曲梁正应力的模拟值与理论值
由表2数据可知,梁上各点正应力模拟值与理论值的相对误差不超过3.8%,模拟结果与理论结果十分相近。同时结合表1数据可知,应力增量的理论值、实测值与模拟计算值均相吻合,验证了此模拟方法的可靠性及模拟结果的准确性,因此可将此模拟方法应用于不同截面梁发生弯曲时正应力与挠度计算,具有较高的理论与实际指导意义。在其他条件不变的情况下,对T形截面梁和工形截面梁进行有限元模拟分析,其纵向正应力的分布情况如图4所示。

a) T形截面

b) 工形截面
由图4可知,工形截面梁的中性轴在其几何中心线上,但梁受挤压的力略大于受拉伸的力,模拟结果比理论更贴切实际;而T形截面梁的中性轴不在其几何中心线上,梁受挤压的力比受拉伸的力大得多,正应力沿梁横截面高度接近按线性规律分布。由图4数据显示可知,在距中性层越远的位置正应力越大,外力对梁的作用主要由距中性层较远处的材料来承担。矩形截面梁的大部分材料靠近中性层,未能充分发挥作用,T形截面梁中性层上下两侧不对称,大部分材料也靠近中性层,而工形截面梁的大部分材料远离中性层发挥了重要作用,因此在工程上受弯曲构件的截面形状宜采用工字形。
3.2 横力弯曲
3.2.1 载荷作用位置
图2中,若2个载荷ΔP/2的受力点为同一个点时,梁将无纯弯曲段存在,而是发生横力弯曲,梁简化后如图5所示,梁上C处为载荷作用位置。例如桥式起重机梁在起吊重物过程中,AC段和CB段便是发生横力弯曲,随着小车的移动,载荷的作用位置不断发生改变,梁发生不同程度的弯曲变形。
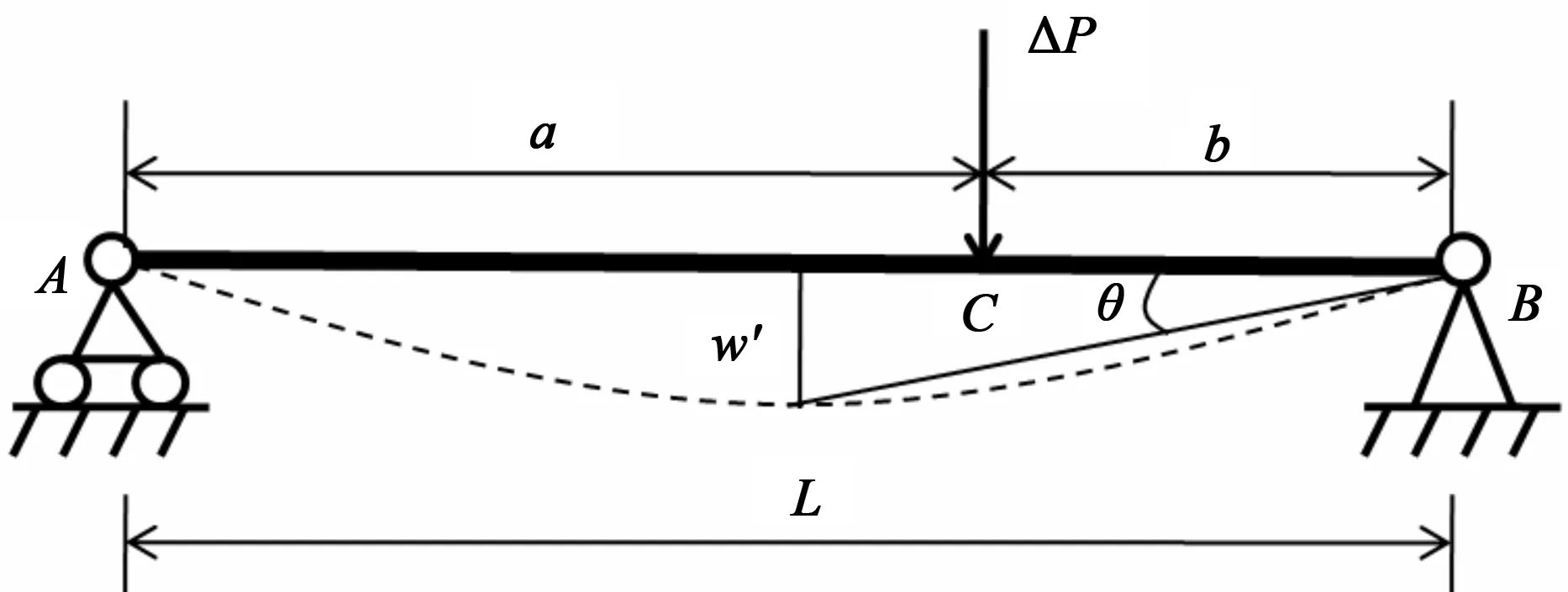
图5 梁的示意图
在工程上,梁的截面形状常选取工形截面,A、B两端受支座的约束,C处到A端的距离为a,到B端的距离为b,θ为发生弯曲变形后梁的坡度,w′为最大挠度值。载荷作用位置变化时,a与b的值也随之变化。
采用仿真模拟方法研究横力弯曲梁的正应力和挠度分布情况。图2中,梁承受2个左右对称的载荷ΔP/2,其挠度由2个载荷分别作用后叠加所得,因此梁发生横力弯曲时的挠度理论值可由式1和式2求得。取梁跨度L=500 mm,ΔP=2 100 N。表3给出了梁最大挠度的理论值与模拟值。
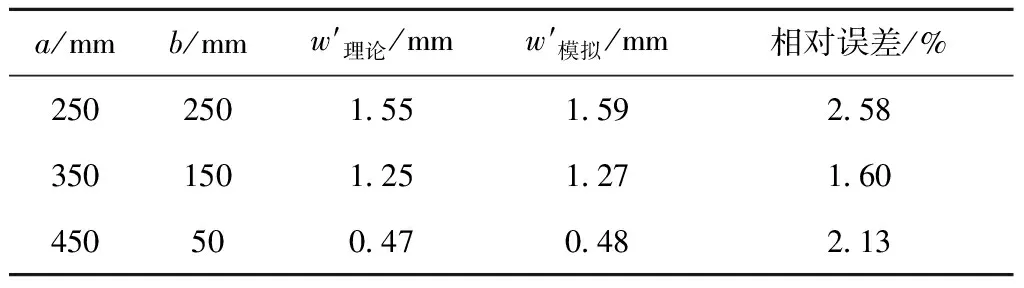
表3 梁最大挠度的模拟值与理论值
由表3可知,横力弯曲梁最大挠度的模拟值与理论值相对误差低于3%,载荷作用的位置越靠近梁跨中点处,梁最大挠度的绝对值越大,因此梁弯曲变形程度的大小不仅与弹性模量有关,也与载荷作用位置有关。使用模拟方法可较准确计算梁上不同位置处的挠度,其模拟结果能为实际工程应用提供有意义的参考。
当载荷作用位置从B端向A端移动时,梁纵向正应力分布情况如图6所示。
由图6可知,当载荷作用位置发生变化时,其轴向应力分布规律不变。载荷作用位置越靠近梁跨中点,梁受到的最大拉、压应力越大;在梁跨中点(即a=b)处达到最大,其引起的弯矩也达到最大,此时梁处于最危险的工况。

a) a=450 mm,b=50 mm

b) a=350 mm,b=150 mm

c) a=b=250 mm
3.2.2 梁跨度
在其他条件不变的情况下,梁受到的最大拉、压应力与其跨度的关系如图7所示,最大挠度、坡度与梁跨度的关系如图8所示。
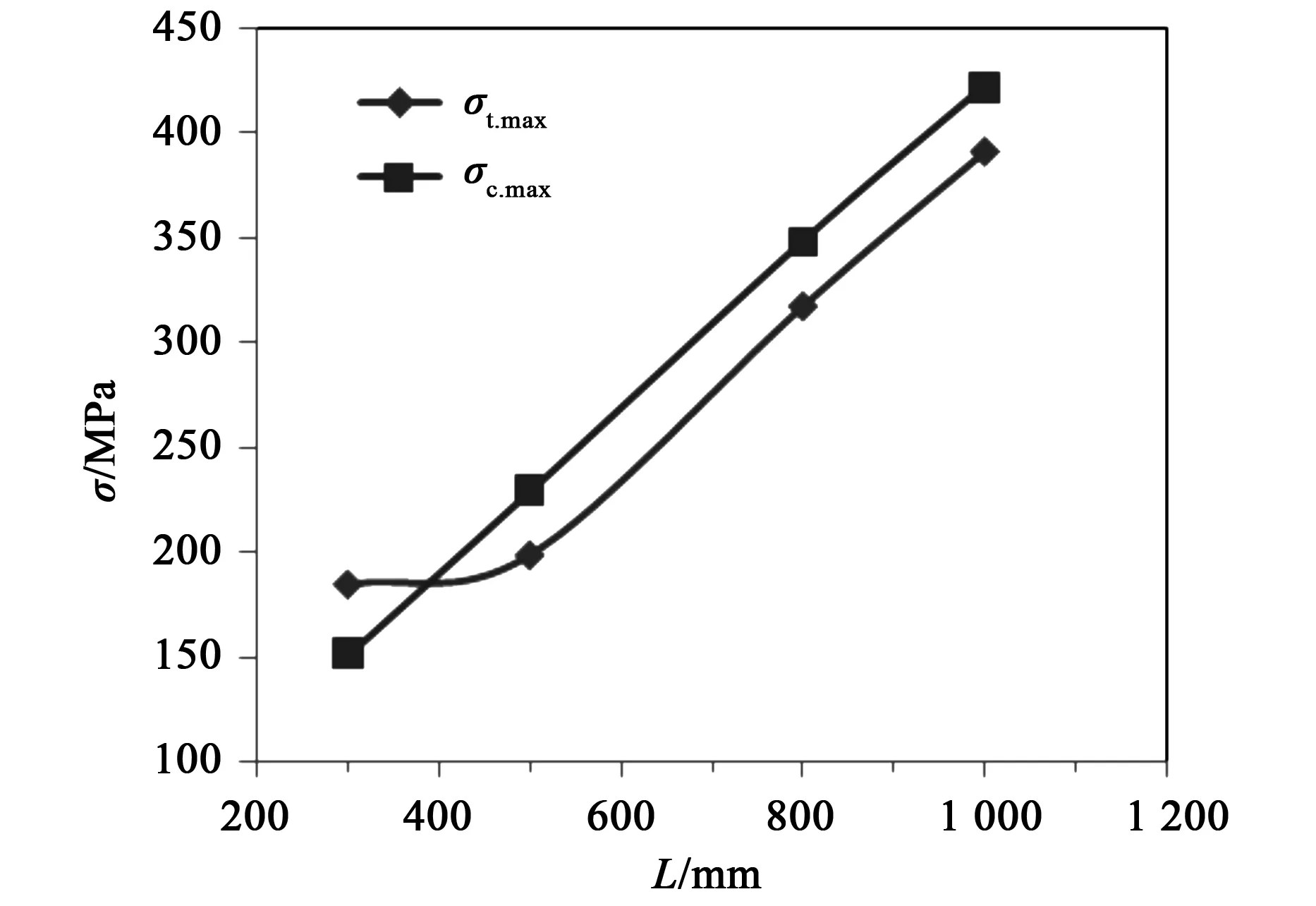
图7 跨度对梁弯曲应力的影响

图8 跨度对梁弯曲变形程度的影响
由图7可知,在相同载荷作用下,随梁跨度的增加,梁受到的最大拉、压应力不断增大,将会引起较大的应力集中;当梁跨度大于500 mm时,压应力比拉应力大,且二者几乎呈线性增大。
由图8可知,在相同载荷作用下,随梁跨度的增加,最大挠度并非呈线性增大,而是先缓慢增大,随后迅速增大;梁跨度和挠度的增大致使梁坡度增大,这对于吊车梁,若其跨度过大,在起吊重物过程中坡度过大,会使小车行走困难,出现爬坡现象。因此可根据实际情况选择合适的跨度,减小梁弯曲应力和变形,避免由于较大的应力集中而产生疲劳裂纹。
4 结语
通过上述研究可以得出如下结论。
1)纯弯曲梁各测点正应力的理论值、试验值与模拟结果值均相吻合,验证了模拟方法的可靠性及模拟结果的准确性。
2)梁发生弯曲时,横力弯曲梁上各点处正应力分布规律与纯弯曲梁一致,沿梁截面高度接近呈线性分布;最大挠度值随梁跨度的变化并非呈线性关系变化。
3)梁弯曲程度的大小不仅与梁弯曲类型、梁跨度及载荷作用的位置有关,还与梁的截面形状有关,在工程上受弯曲构件的截面形状适宜选用工形截面。
