基于粒子群优化算法的温度示踪渗漏探测应用研究

2022-06-28张国新李小雨颜书法

东北水利水电 2022年5期

张国新，陈亮，李小雨，颜书法

（1.中电投蒙东能源集团有限责任公司扎哈淖尔工业供水分公司，内蒙古通辽 028000；2.河海大学岩土力学与堤埋工程教育部重点试验室，江苏南京 210098；3.河海大学岩土工程科学研究所，江苏南京 210098）

0 引言

据调查研究显示，由渗透破坏造成堤防和大坝破坏的事故占大坝失事事故的40%以上[1]。渗漏会造成土体颗粒流失，如果任由渗漏发展会进一步形成集中渗漏通道，将可能导致坝体塌陷或滑坡，甚至形成决堤，造成严重后果[2]。受堤坝规模、材料和地形、地质条件的影响，堤坝往往存在多个集中渗漏通道，如果不能探测出全部渗漏通道，在主要通道进行治理后，次要渗漏通道会逐渐发展成主要通道，继续对堤坝造成危害。因此，有必要对堤坝进行全面摸排，找到所有渗漏通道，进行彻底加固。

目前，用于堤坝渗漏探测的技术主要有物探法[3]、同位素法[4]和温度示踪法[5-7]。物探法包括高密度电法[8]、瞬变电磁法[9]和地质雷达法[10]。由于渗漏一般处在堤坝深层，在含水层中物探信号会受到强烈干扰，导致探测效果不明显。同位素测定则成本昂贵，对环境也会造成一定的污染。温度场属于地层的天然物理场，通过测量地层不同部位的温度值，可以得到整个地层连续的温度场。因此，利用温度场对渗漏通道进行探测，具有成本低、效率高等优点。

20世纪50年代，国外将地温运用于堤坝渗漏探测[11]，目前，温度探测主要用于对大坝渗漏的定性分析，缺乏对渗漏通道的定量计算。本文基于已有的多个集中渗漏通道温度场探测模型，建立反分析目标函数，通过粒子群优化算法[12]优化目标函数中的参数得到集中渗漏通道中心位置，并与同位素示踪结果进行对比，证明此优化算法可以运用在温度示踪确定大坝集中渗漏的中心位置。

1 多个集中渗漏通道反分析

1.1 温度示踪原理

渗流是土体中普遍存在的现象。渗流过程中流速缓慢，土和水之间有充分的时间进行热量交换，因此，在渗流过程中，岩土体和水的温度是相同的。发生渗漏时，水流流速变快，岩土和渗漏水没有时间进行充分的热量交换，渗漏水仅仅与附近土体发生部分热量的交换。因此，渗漏附近的温度场与渗流部分的温度场存在明显差异，离渗漏中心越近，这种差异越明显，整个地层形成了具有一定特征的温度场。

1.2 数学物理模型

正常渗流情况下，基于单个渗漏通道的一般热传导物理问题的数学模型：

式中：M为渗漏通道到某点x的温度函数；L0为渗漏通道的中心位置；T（x，t）为堤坝x测点t时刻的温度值。

由于所采用的数学模型是线性的，温度又是标量值，运用叠加原理可得n个集中渗漏通道下的一般热传导物理方程数学模型：

式中：n为集中渗漏通道的数量；Loi为第i个集中渗漏通道的位置；T(xj，t)为堤坝xj测点在n个集中渗漏通道作用下t时刻的温度值。

在构建数学模型时，将渗漏通道的中心作为坐标原点，构建了热传导方程。在实际测量中，并不知道渗漏的位置。因此，往往将某个探测孔的地面高程作为坐标原点。想要运用上述方程，就必须要把探测坐标系统下测点的坐标转换为以渗漏通道中心为原点的坐标。为此，采用转换尺度无变化的Brusa-Wolf六参数模型，图1是以渗漏通道中心为原点的坐标系统O和探测坐标系统O′之间相互关系示意图。转换公式如下：

图1 模型坐标O与探测坐标O′转换示意图

式中：x，y，z为测点在热传导模型中的坐标值；αx，αy，αz为欧勒角；x′，y′，z′为测点在探测坐标系中的坐标值；X0，Y0，Z0为热传导模型坐标原点O在探测坐标系中的坐标值；矩阵R如下：

因此，可得在热传导模型坐标系下，测点j在n个集中渗漏通道作用下的温度：

式中：Tj为测点理论温度值；Tji为测点j在集中渗漏通道i单独作用下的温度值；C1i，C2i为第i个渗漏通道产生的温度场解析方程的未知参数；lji为测点j到集中渗漏通道i中心的距离

1.3 目标函数的构建

在实际工程中，通常会通过测量部分位置的温度来计算式（2）中的参数。通过观测数据求解数学物理模型中的参数问题称为反问题。但是，观测过程中，由于人为偶然误差和测量仪器的系统误差，观测量一般可表示：

式中：为j点温度观测值；εj为误差。

此处主要研究多个渗漏通道在同一平面同一深度的情况，因此，式（5）可以简化成：

式中：Xoi为第i个渗漏通道中心的横轴坐标值。

为此，最小二乘法最优化目标函数为

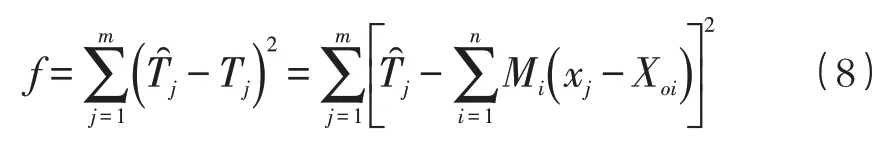
式中：m为测点个数。

2 粒子群优化算法

粒子群优化算法（Particle Swarm Optimization）是由KENNEDY等于1995年提出的一种模拟鸟类觅食行为的智能算法。PSO利用鸟群中个体对信息的共享机制，使得整个鸟群朝食物最多的方向运动。PSO算法中有2个参数：速度和位置。通过每一次迭代后对适应度函数进行评价，不断调整速度和位置，最终达到全局最优值。具体表现见图2。

图2 粒子群优化算法流程图

每次迭代后速度更新公式：

式中：t为当前迭代次数；w为惯性权重；vi（t）表为当前粒子i的速度；c1，c2为学习因子；rand1和rand2为取值0～1之间的随机数；pi（t）为当前粒子i的个体极值；xi（t）为当前粒子i的位置。

位置更新公式：

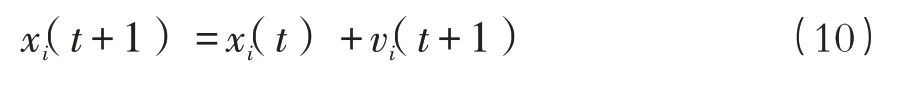
式中：xi（t+1）为第t+1次迭代开始时粒子i的位置。

优化过程中，为了避免陷入局部最小，动态调整加速度因子和惯性权重。每次迭代后，w，c1和c2可表示：

式中：wmax为迭代过程中惯性权重的最大值，取wmax=1.4；wmin为迭代过程中惯性权重的最小值，取wmin=0.7；tmax为最大迭代次数，取tmax=500。

式中：c1max为迭代过程中学习因子的最大值，取c1max=2.5；c1min为迭代过程中惯性权重的最小值，取c1min=0.7。

文中每次迭代过程中c2取值与c1相同。

3 工程实例应用

3.1 工程概况

某坝水库工程等级为Ⅲ等，主要建筑物级别为3级，次要建筑物级别为4级。坝顶长1 230.00 m，坝顶宽3.50 m，坝顶高程953.80 m，最大坝高21.60 m。上游坝坡采用模袋混凝土护坡，坡度为1∶3.5。下游坝坡为碎石护坡，在940.00 m处设有马道，马道宽2.50 m，马道以上坡度为1∶3.0，以下为1∶3.5。河床覆盖层截渗采用悬挂式混凝土心墙，心墙分布桩号为0-150～0+520和0+730～0+770，墙深25.00 m，墙厚1.20 m。

该水库自2008年蓄水以来，出现渗漏主要分布在桩号0+200，0+250及桩号0+700～0+900附近，大部分区域坝后坡脚潮湿，后期对大坝进行加固，加固后发现在下游排水沟仍然存在一股渗漏量较大的稳定渗漏水。为此，在马道布置16个勘探孔，从左到右孔号分别为ZK8到ZK23，孔深18.00 m，入基岩5.00 m，16个勘探孔一字型排开与坝轴线平行。

3.2 温度反演

钻孔完成后，静置钻孔2 d，等钻孔中的流速场和温度场恢复到本底之后开始对这16个钻孔进行温度探测，进行了一周探测后发现每个钻孔的最低温度在16.00 m的位置，这16个钻孔的16.00 m温度见图3。

图3 各孔最低温度分布情况

从图3中可以发现，在ZK17附近存在明显的异常低温区，因此，在ZK17附近肯定存在一条明显集中渗漏通道。首先，式（7）中n=1，利用单集中渗漏通道热传导模型式进行数据拟合，拟合的温度曲线如图4单个集中渗漏通道温度拟合曲线所示，C1，C2，Xo分别为0.08，9.0和600。各点拟合残差结果见表1。

表1 各孔温度残差分布情况

图4 单个集中渗漏通道拟合曲线

从图4中发现，实测数据点离散分布在拟合曲线的上下侧，为了使各测点温度对单个集中渗漏堤坝温度曲线异常程度具有可比性，把拟合曲线整体向上移动，移动量为0.36。此时各点的残差即为表1中修正后的残差，残差值越大，代表测点处越有可能存在其他渗漏通道。利用3次样条曲线对修正后的残差值作插值曲线，如图5所示，由曲线的波谷数量确定所有渗漏通道的位置。图5中共发现了5个波谷，其中波谷1经过分析认为是由于勘探范围的限制，未能完全揭示可能存在的渗漏通道，这种情况求得的渗漏通道位置误差较大，因此不考虑这部分的异常。其余4个波谷认为是由于渗漏通道造成的，因此，除了在17号孔附近还存在另外3个渗漏通道。

图5 3次样条插值曲线

通过3次样条插值曲线确定了4条渗漏通道，因此，在目标函数中一共有12个参数：C11，C21，Xo1，C12，C22，Xo2，C13，C23，Xo3，C14，C24，Xo4。采用粒子群优化算法初始化10个12维粒子，利用Python编制优化算法进行500次迭代后，目标函数收敛，收敛过程见图6，计算结果见表2。

表2 计算参数结果

图6 优化过程

将优化后的参数带入式（7），目标函数方差为0.838，优化曲线见图7，各点残差值见表1中优化后的残差一栏。

在图7中明显可以看到2条主要集中渗漏通道，其中心位置为600.00 m和910.00 m。此外,还有2条次要集中渗漏通道，它们的中心位置为517.47 m和664.60 m。

图7 多通道温度优化曲线

3.3 同位素示踪试验

为了进一步说明温度示踪法和粒子群优化算法在渗漏探测中的可靠性，选择同位素示踪试验，测试8～23孔的流速，经过测试，得到各孔16.00 m位置的流速见图8。从图8中可以发现：在ZK17和ZK22附近存在明显较大流速，流速超过1.00×10-4cm/s，而在次要集中渗漏通道附近流速较小。ZK17的位置正好是600.00 m，所以，此处流速和温度相符合，流速大，温度低。ZK22离主要渗漏通道1还有10.00 m的距离，ZK22存在大流速，从侧面说明主要集中渗漏通道已经发展到了此处。从图7也可以看出主要渗漏通道1已经包含了ZK22，而ZK15和ZK18流速正常，从侧面说明次要渗漏通道规模较小，还没有形成大规模的集中渗漏通道。