地铁车站自然通风模型实验研究
2022-06-28肖益民渠永通陈永江曹树勇
曾 臻 ,肖益民,渠永通,陈永江,曹树勇
(1. 中铁二院工程集团有限责任公司,成都 610031;2. 重庆大学,重庆 401331)
1 研究背景
自然通风作为一种常用的被动节能措施,具有很好的节能潜力和较高的应用价值,在民用建筑中常被广泛采用。因此,将自然风引入地铁车站,对其空气品质的改善和节能具有重要意义[1-5]。然而,针对地铁车站自然通风的相关研究,尤其是与自然通风效果有关的研究较少,其有效应用方式、应用效果和价值有待进一步深入探究。
在当前地铁环控设计过程中,基本未考虑自然通风对地铁车站的能耗影响[6],造成了设备容量事实上的冗余过剩。笔者通过对地铁车站自然通风模型实验台的搭建,结合实验数据,得到了过渡季不同通风工况下地铁车站的自然通风效果,并给出了地铁车站公共区充分利用自然通风的方式和建议,为地铁车站的设计和运营提供了参考,具有良好的工程应用前景和节能潜力。
2 模型实验
2.1 相似理论
相似理论是模型实验的依据,为实现两个流动问题的力学相似,必须先保证几何相似、运动相似、动力相似,以及两个流动的边界条件和起始条件相似。同时,地铁站内存在大量的发热体,导致通风空调系统的送风温度必然低于站内的空气温度,即送风气流属于非等温射流,其表现为重力和浮升力的不平衡。本研究采用阿基米德数Ar 来代替表征重力相似的弗诺得数,它们在重力作用上相差一个乘数Δρ/ρ0,其中Δρ 是送风气流和工作区气流的密度差,ρ0为送风气流密度。综合阿基米德数Ar、气体状态方程和热平衡方程,可以得到热量阿基米德数为
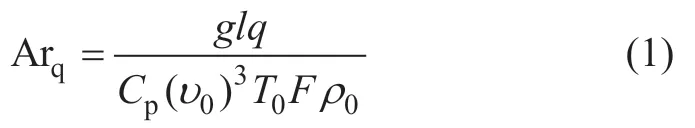
式中:T0为送风气流温度,℃;q 为站内余热,W;Cp为空气定压比热容,J/(Kg·K);υ0为平均送风风速,m/s;F 为送风口的面积,m2;ρ0为送风气流空气密度,kg/m3;Arq为热量阿基米德数。
最终拟以Arq代替Ar,实际上是用室内余热量q取代反映浮升力作用的温差ΔT0,从而使其包含的各个参数均成为工程应用中可知或者可控的参数。
2.2 相似比例尺
确定模型的几何比例尺Cj,一般认为Cj越大,越容易真实地模拟原型,但Cj越大,模型的造价越高,需要的试验场地越大,试验观察的难度就越大。在充分考虑了试验经费和试验场地的实际情况后,确定本次模型试验的几何比例尺为Cj=1∶20。根据沙坪坝地铁站的原始内部空间尺寸和几何比例尺Cj=1/20,确定模型的内部空间尺寸,如表1 所示。

表1 原型和模型内部空间尺寸 Table 1 Summary of internal space dimensions of the prototype and the model mm
模型主体结构的几何尺寸严格按照原型进行设计制作,同时把一些对实验结果影响很小的结构进行简化处理。其中,站厅层原型为微拱形,模型将站厅层处理为长方体,站台层根据原型尺寸搭建,只考虑一辆列车到站、站台门打开时的情况,因此只在一侧方向上设置24 个站台门,每个站台门开度2 m,高度2 m,另一侧不设置站台门以及站内隧道。站内隧道长度按160 m 的原型尺寸考虑,涵盖了车站两端的活塞风井和排热风井。与站台方向平行的隧道部分宽3.8 m,高5.0 m,地铁列车采用A 型车辆,6 辆编组,全长120 m,宽度3 m,高度3.8 m。模型主体结构及搭建完成的实物实验台如图1 所示。

图1 搭建完成的实物实验台 Figure 1 Completed physical test bench
3 测点布置
3.1 发热量及热源尺寸
地铁车站内部热源主要有设备散热、照明散热、人员散热以及站台门传热等,根据相似理论所确定的几何比例尺Cj=1/20 和热量比例尺Cq=1 789,结合当前设备设计容量,可以计算出模型内部设备的几何尺寸和发热设备的发热量。
发热设备按所处位置可分为3 类:第一类位于楼板上,如自动售票机、安检设备和进出闸机等;第二类位于壁面上,如广告牌、指示牌以及站台门传热等;第三类则位于天花板上,如照明设备、线缆发热等。对于第一类发热设备,可按照就近原则,将多个热源组合为一个发热体,并采用电阻值为133Ω/m 的碳纤维发热线外包薄壁铁皮外壳来模拟;对于第二类发热设备,可直接将碳纤维发热线均匀粘贴于模型内侧壁面;对于第三类发热设备,可在对发热线上部做隔热处理的基础上,将发热线均匀粘贴在对应层顶板上。此外,由人员分布具有随机性,可将该发热量视为站内单位面积的均匀热源,并简化为以碳纤维发热线为实验热源的“线型”热负荷。地铁站内第一类发热设备的外壳尺寸及布置如图2 所示。
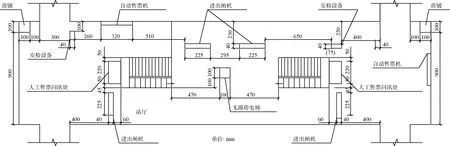
图2 站厅层第一类发热设备尺寸及布置 Figure 2 Dimension and layout of class I heating equipment on the station hall floor
3.2 隧道通风系统设计
重庆地铁1号线沙坪坝站采用全封闭站台门系统,在该系统的列车运行及空调散热量中,50%以上释放在车站车行道[7]。为了准确模拟真实情况,需要在模型实验台设置通风排热系统来控制隧道内的温度。由于隧道和站台空气流动处于阻力平方区,站台门处等效局部阻力系数只与其几何形状有关,因此在制作模型时,要严格根据实际隧道、列车及站台门的实际尺寸按相似比例制作。隧道活塞风对地铁车站的影响呈周期性正负压作用,因此在一定的周期内,影响车站自然通风效应的主要因素为车站隧道排热风机。为了能够实现对地铁车站间歇性负压效应的模拟,实验台在隧道两侧安装有两台风机,以模拟列车停站、站台门开启时的工况条件。
3.3 温度测点和工况安排
地铁站温度场和速度场的分布情况需通过专业仪器测试得到,因此,模型实验台设计中需根据站内结构和设备布置,合理地确定温度和风速测点。其中,温度测点按均布原则分别在站内公共区中部、主体附属接口和出入口通道,按实际距离约900 m 间隔设置;风速测点则位于各出入口通道中部,截面内采用九点法均匀布置。站厅层温度测点布置方案如图3 所示。

图3 站厅层温度测点布置 Figure 3 Layout of temperature measuring points on station hall floor
本模型实验共安排了6 组实验工况,其中:1~3组工况为出入口之间无高差工况,重点通过改变站内设备的运行工况,以便来观察车站自然通风规模的变化情况;4~6 组工况为车站内部发热量一致的工况,重点通过改变出入口之间的高差,以便来观察该因素对车站自然通风规模的影响。具体工况安排如表2 所示。
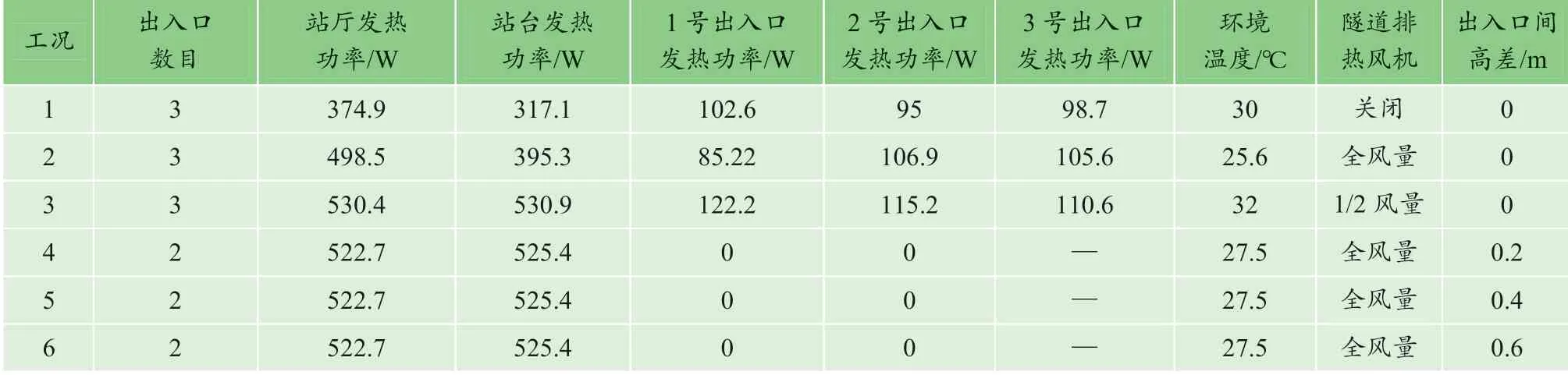
表2 模型实验工况安排 Table 2 Working condition schedule of model test
4 结果分析
4.1 内部发热量的影响
根据既定的实验工况,开启对应的设备,进行测点温度和出入口风速的测试,并将不同工况下的测试结果记录汇总,形成模型实验工况1~3 的实测结果,如表3 所示。另外,需要特别说明的是:表中所有的测试数据均为多点、多次实测结果的平均值,以避免测试过程中的偶然误差对结果造成不利的影响。

表3 实验工况1~3 的实测结果 Table 3 Summary of measured results under test conditions 1-3
其中:+表示进风,自然风从室外吹入地铁车站;-表示出风,地铁车站排风至室外。从测试数据可以看出:工况1 由于热压作用,自然风从1 出入口通道引入,流经站厅层和站台层,温度逐渐升高,再从2 和3 出入口通道流出,即自然通风客观存在且规模可观,工况2、3 亦有类似结论。同时,工况1~3 的测试结果均表明:在站厅层实测发热功率比站台层更大的情况下,站厅平均温度更低,且温度分布均匀,在相同条件下,流经站台层的通风规模较站厅层的更小,即该通风规模中的较大部分路径主要由出入口通道+站厅层+出入口通道组成。
工况2 在开启全部风量的排热风机后,其自然通风的规模和方向与工况1 十分接近,且两个工况下站厅层与室外空气平均温度的差值分别为15℃和15.1℃,热压作用亦基本相同。因此,可以得出:车站隧道通风系统对自然通风量的影响作用不明显,在无室外风压作用的情况下,自然通风的主要动力来源为站内热源释放热量所形成的空气热压。工况3 将隧道排热风机的风量调整为1/2 后,1 号和2 号出入口通道的通风方向反向,但总的通风规模变化不大。结合前述分析不难得出:车站隧道通风系统虽然对自然通风规模的影响作用十分有限,但站内热压所形成的空气流动方向本身具有不确定性;在包含车站隧道通风系统在内的外部条件变化的影响下,形成了特定方向的初始通风流向,并在后期热压作用的自然通风过程中维持不变。
同时,通过测得的壁面温度以及站内不同区域温度,可估算得到各区域向围护结构(实际车站为土壤)的总散热量,其中站厅、站台、出入口通道可以计算其当量直径,将它们近似于水平管道来进行计算,站厅层表面传热系数取1.41 W/m2·℃,站台层取1.86 W/m2·℃,出入口取2.32 W/m2·℃,最终算得的散热量如表4 所示。
可以看出:无论是站厅层、站台层还是出入口,工况1 站内环境向围护结构的传热量均相对较大;工况2 将排热风机开启后,由于隧道通风系统对车站轨行区的排热影响,轨行区壁面温度较低,但受室外空气温度(实验工况下与环境温度为同一温度)降低更多的影响,它向围护结构的总传热量反而减小,导致自然通风需带走更多的站内热量;当工况3 在工况2 的 基础上调小隧道通风规模时,虽然受车站轨行区通风规模减小的影响,轨行区维护结构的壁面温度略有提高,但此时环境温度升高明显,站台层向围护结构的总传热量增加,在站内发热功率差异不大的情况下,自然通风进、排风温差明显减小。因此,可以得出结论:自然通风对地铁车站的排热作用受室外环境温度的影响较大,实验结果与理论分析一致。

表4 实验工况1~3 围护结构的散热量 Table 4 Heat dissipation scale of enclosure structure under test conditions 1-3
4.2 出入口间高差的影响
实际车站的出入口受地面地坪高度的影响,不同出入口之间存在一定的垂直高差,尤其是在类似于重庆这种山地城市中,体现更为明显。为了进一步探究出入口间的高差对车站自然通风规模的影响,在维持站内散热量等条件不变的前提下,进行了工况4~6的模型测试,测试过程中环境温度保持27.5℃不变,测试结果如表5 所示。
从测试数据可以看出,当两个出入口之间高差分别为0.2、0.4 和0.6 m 时(几何比例尺Cj=1/20,即4、8 和12 m),由于热压作用,自然风均从3 号出入口通道引入并流经站厅层,吸收站内余热后温度逐渐升高,再从1 号出入口通道流出。在这3 种高差情况下,模型实验台内部的温度场以及壁温几乎没有什么变化,散热量基本相同,3 号出入口通道由于排风,其平均温度明显高于1 号出入口通道的平均温度,得到的散热量如表6 所示。
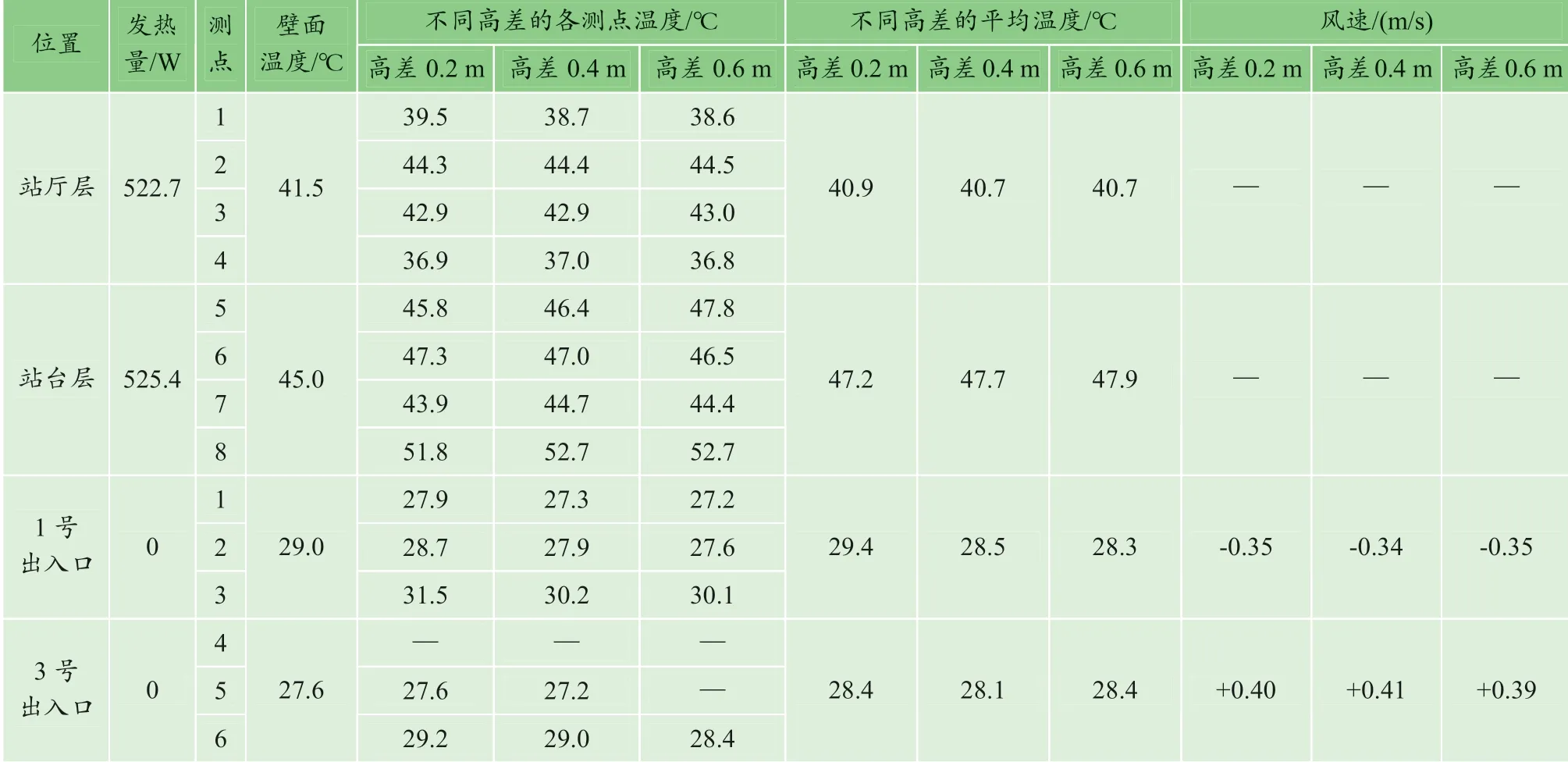
表5 实验工况4~6 实测结果汇总 Table 5 Summary of measured results under test conditions 4-6
工况4~6 的条件仅改变了出入口间的高差,包括围护结构散热量在内的其他条件均保持一致,且最终得到的各工况通风规模差异不显著。因此,可以得出:在其他条件不变的前提下,车站各出入口间的高差在一定范围内的变化,并不会对通风规模产生实质影响,它对自然通风的影响作用有限。

表6 实验工况4~6 围护结构散热量 Table 6 Heat dissipation scale of enclosure structure under test conditions 4-6
5 结论
因场地等因素限制,本实验中所使用的实验台没有进行妥善的保温处理,在实验过程中,通过采取放大实际发热量的方式来补齐外部传热损失,以保证实验测试的准确性。通过对比分析各工况的实测数据,可以得出以下实验结论:
1) 自然通风客观存在且规模可观,其中的较大部分路径主要由出入口通道+站厅层+出入口通道组成,流经站台层的通风量相对较少。
2) 热压是地铁车站自然通风的主要动力之一,主要受地铁车站埋深以及内部发热量大小的影响,而车站隧道通风的运行状态对自然通风规模的影响十分有限。同时,自然通风对地铁车站的排热作用受室外环境温度的影响较大,就实验测试工况而言,测试范围内室外温度升高5℃,排热作用降低30.1%。
3) 车站隧道通风系统虽然对自然通风的规模无影响,但因热压驱动的空气流动方向本身具有不确定性,所以隧道通风系统客观上决定了自然通风的初始流向,并在外部条件不发生改变的前提下始终维持不变。
4) 改变出入口间的高差可以改变自然通风的热压驱动力,但由于外部条件的制约,出入口间的高差不可能无限增加,在测试对应的实际高差4~12 m 范围内,出入口的高差对自然通风规模的影响不大。
