圆振动弛张筛动态结构特性分析

蒲坤玮，王新文，徐宁宁，于 驰，乔德正，郭 进，李保岐

(中国矿业大学(北京) 化学与环境工程学院，北京 100083)

在筛分粘湿细粒级物料时，细粒物料容易在筛面上发生粘聚成团等情况[1]，从而造成筛分设备处理能力下降、筛分效果变差等问题。弛张筛作为潮湿细粒物料深度干法筛分的新型筛分设备，它突破性地解决了粘湿细粒物料筛分这一国内外筛分技术的难点[2]。随着振动筛大型化、重型化和标准化的发展，对筛机结构的振动强度的要求也相应增加。在设计阶段，对筛机进行动态特性分析是必要的，同时对计算模态分析结果的准确性有更高的要求。近年来，研究者对单质体振动筛动态结构特性的研究较多，对弛张筛动态结构特性的研究较少。柴保明等人[3]，采用有限元软件对单质体振动筛进行计算模态分析，得到筛机各阶的固有频率和振型，并在此基础上，优化了振动筛的结构，提高了筛机的可靠性。沈高飞等人[4]，对单质体振动筛进行实验模态分析，得到了各阶模态参数，分析了筛机结构在设计上存在的问题，为后续模型的修正和结构优化设计提供参考。洪瑞[5]为研究弛张筛中剪切弹簧的橡胶动态特性，采用有限元法和模态实验分析法进行对比研究，验证了有限元法的准确性。王宏等人[6]，采用有限元软件对弛张筛进行了模态分析，得到前八阶固有频率和振型，找到了筛机合适的工作频率，同时进行了应力分析，通过对比结果，验证了筛机结构的合理性。上述讨论可看出，针对弛张筛复杂的机械结构，有些研究者以某个关键部件进行动态特性分析，有些研究者对整机进行计算模态分析，但是，目前鲜有研究者在考虑筛机与实际一致边界条件的同时，将弛张筛计算和实验得到的模态分析结果进行比较。

本文对0827型圆振动弛张筛采用有限元法进行预应力模态分析[7]，同时通过力锤法对筛机进行模态测试，对比这两种模态分析结果，优化筛机结构，验证此种有限元法模态分析的准确性，为后续大型振动弛张筛采用有限元法进行动态结构特性分析的合理性和可靠性提供依据。

1 圆振动弛张筛结构及工作原理

圆振动弛张筛是在传统圆振动筛的基础上发展而来，其结构如图1所示，主要由主动筛框、浮动筛框、惯性激振器、剪切弹簧、隔振弹簧、聚氨酯筛板以及加强梁等零部件组成。主动筛框与浮动筛框之间通过剪切弹簧弹性连接，属于双质体振动系统[8]。圆振动弛张筛通过单一激励就可产生双重振动，其中，基本振动是偏心块旋转带动主动筛框产生圆形振动，附加振动是连接主动筛框与浮动筛框的剪切弹簧在主动筛框的作用下，使浮动筛框产生椭圆形振动[9]。主动梁与浮动梁交叉布置，由聚氨酯筛板连接，当主、浮筛框产生相对运动时，筛板发生周期性连续地往复张紧、松弛，产生大挠度形变，从而实现细粒度物料的筛分。

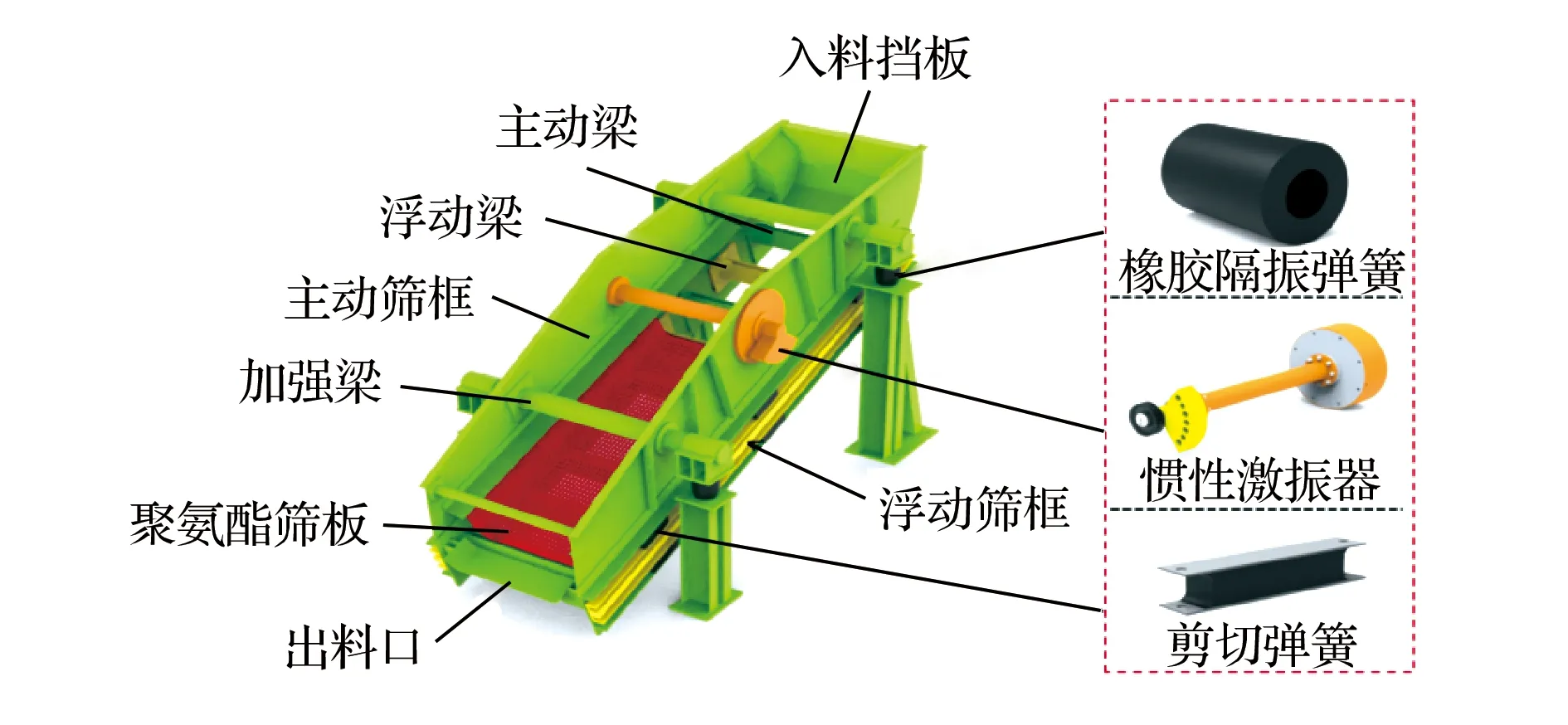
图1 圆振动弛张筛结构

2 模态分析

2.1 模态分析理论基础

模态分析是以振动理论为基础，以获取机械结构模态参数为目标的分析方法。机械结构的每一阶模态均有特定的固有频率、阻尼比、振型和模态刚度等模态参数。这些模态参数既可以通过有限元法(FEM)来获取，又可以通过实验测试(EMA)来获得[10]。其中，运用有限元法对振动结构进行离散，建立系统特征问题的数学模型，用各种近似方法求解模态参数的过程，称为计算模态分析；通过实验测得激励和响应，运用数字信号处理技术获得传递函数，运用参数识别方法，求得系统模态参数的过程，称为实验模态分析[11]。由于本文研究内容是对圆振动弛张筛进行计算模态和实验模态分析及对比，因此，获取振动弛张筛的固有频率和振型是该研究的主要内容。

圆振动弛张筛是多自由度振动系统，由振动理论可知，其微分运动方程为：

式中，[M]为质量矩阵；[K]为系统刚度矩阵；[C]为系统的阻尼矩阵；X、F(t)分别为系统各点的位移响应矢量和激励力矢量。

当激励力矢量F(t)为零时，式(1)变为结构系统的自由振动微分方程，对系统结构振动进行分析时，由于系统阻尼影响很小，故忽略，这样便得到系统无阻尼自由振动方程，即：

设系统做简谐振动，即：

X=X0sin(ωt)

(3)

将式(3)代入式(2)中，得到：

([K]-[M]ω2)X=0

(4)

求解式(4)的广义特征值，即为系统自由振动的固有频率ωi，此时Xi即为系统的振型向量。

2.2 圆振动弛张筛预应力模态分析

2.2.1 有限元模型的建立

针对0827型圆振动弛张筛建立双质体振动系统的有限元刚柔耦合模型，即在Solidworks中绘制简化的圆振动弛张筛三维模型，并保存为STEP格式文件，然后将STEP格式文件导入Ansys R17.0软件中，完成有限元模型的建立。对于较复杂的振动弛张筛实体模型，在进行有限元分析时，不能完全按照实体模型进行仿真分析，需要合理地简化操作[12]。本文在误差允许范围内，在几何建模平台中，忽略圆振动弛张筛结构上一些不重要的特征[13]，如聚氨酯筛面等非承载结构件以及主、浮筛框上的定位和安装孔结构，从而在网格划分阶段，使网格数量减少，提高网格质量、模型计算效率和准确性。运用布尔求和运算[14]处理筛机螺栓连接和焊接等刚性连接方式，以避免结构件的非线性耦合，如主动筛框的侧板、角钢和主动梁的连接，浮动筛框上连接槽钢与浮动梁的连接，均通过布尔求和成为整体，如图2所示。

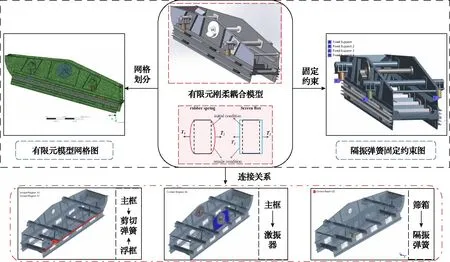
图2 有限元模型

为了能够获得相对真实的圆振动弛张筛模态分析结果，需要对弛张筛的材料参数进行定义，主、浮筛框采用低碳钢，而柱形橡胶隔振弹簧和剪切弹簧的材料均为橡胶，具体参数见表1。

表1 材料物理参数

2.2.2 边界条件及网格划分

考虑到圆振动弛张筛实际的工作状况，在圆振动弛张筛模型的隔振弹簧底面定义固定约束[15]。在综合考虑计算效率和精度的前提下，保证网格相关度不变，设置网格相关中心为中等，网格尺寸为5mm，进行自由网格划分，之后对连接振动弛张筛主动筛框和浮动框的剪切弹簧进行细化处理，该振动筛共划分2160864个单元，4237186个节点。偏斜系数(Skewness)是用来判定网格形状是否接近理想状态的指标，表示单元相对其理想形状的相对扭曲度量，0 最好，1 最差。由网格质量评估可知，整体网格的平均偏斜系数为 0.36，处于 0.25～0.5 范围内，说明网格质量较好，如图3所示。

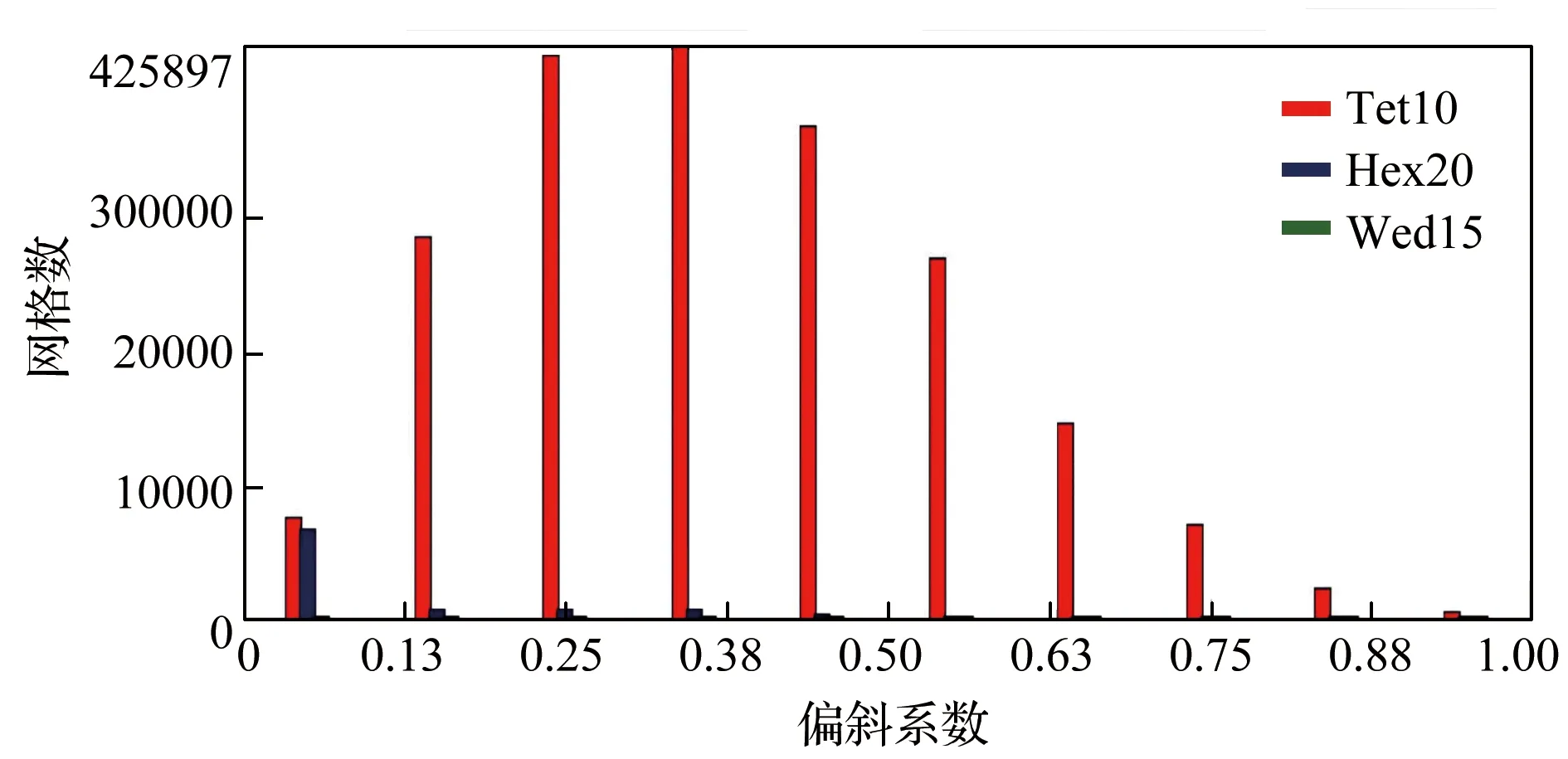
图3 网格质量评估图

2.2.3 筛机计算模态分析结果

为了获得与实际振动弛张筛一致的边界条件，在计算模态前先对振动弛张筛进行预应力分析[16]，具体：第一步，筛机隔振弹簧采用固定约束，对筛体施加重力加速度，进行静力学分析；第二步，将静力学分析的结果作为筛机模态分析的预应力，对圆振动弛张筛采用经典的Block Lanczos法[17]进行预应力模态分析，设置提取模态阶数为11，得到各阶固有频率，见表2。前十一阶固有频率下的部分模态振型如图4所示。

0827圆振动弛张筛的工作频率为11.67Hz，位于计算模态结果的第7阶固有频率14.888Hz之后，故实验测试筛机模态时，应侧重于低频区间模态参数采集。由图4可看出，前9阶模态振型均为筛机的刚体模态，其模态振型相对简单，故采用力锤法进行实验模态分析时，筛机上布置的测点数量可以相对减少，同时因低阶频率相对集中，故实验测试的采样频率设置要低一些，每次采样点数设置要高一些，以在低频区间得到较高的测试分辨率。

表2 前十一阶固有频率(FEM) Hz

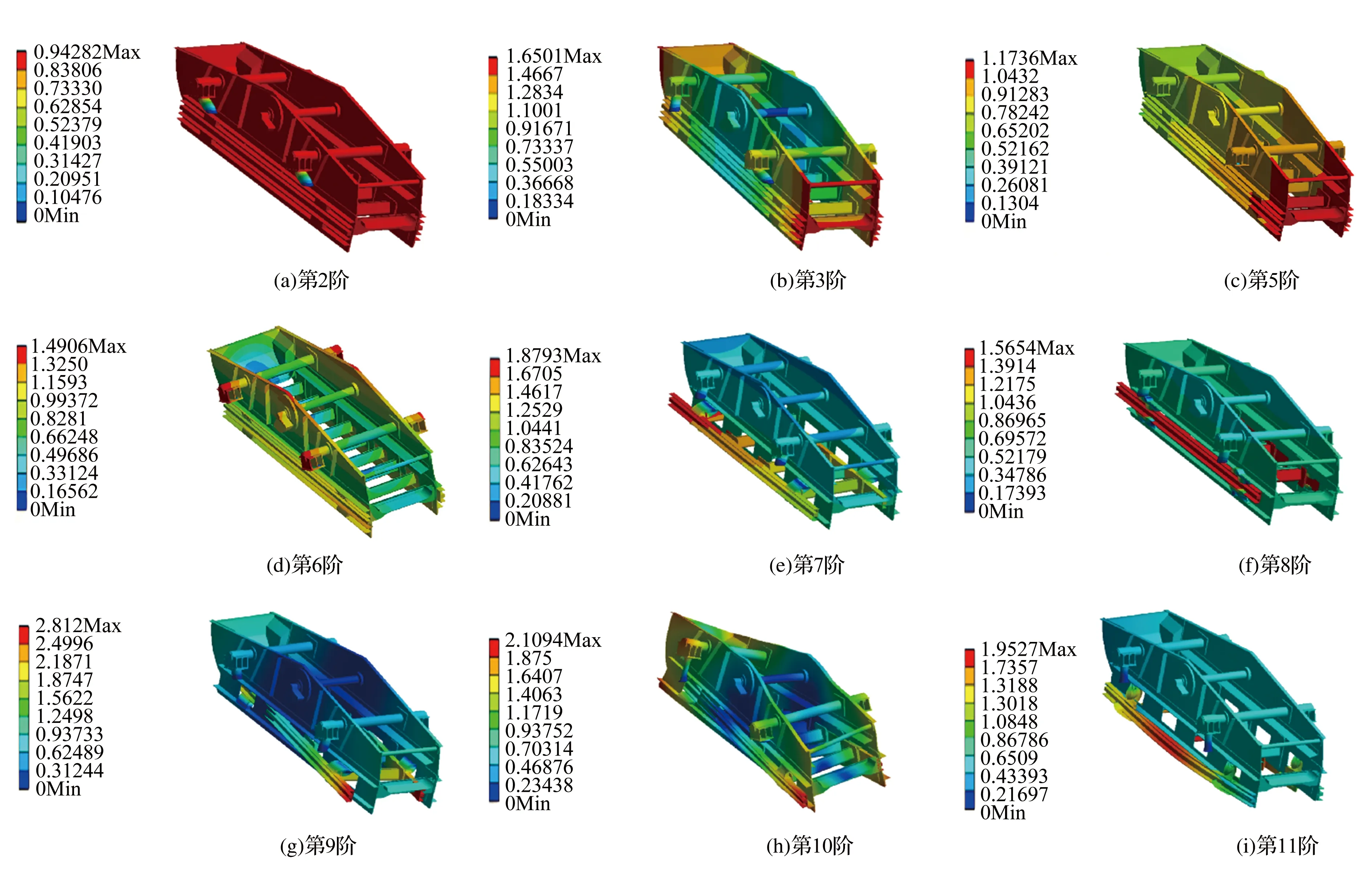
图4 1-11阶部分模态振型(FEM)

2.3 圆振动弛张筛实验模态分析

实验模态分析(EMA)是研究机械结构振动的非常重要的方法[18]，它通过分析测试过程中激励信号与对应的响应信号，建立频响传递函数，选取合适的参数估计方法收取系统的模态参数。

因圆振动弛张筛是平面对称结构，故根据有限元法模态分析结果，在试验筛机上对称布置测点位置，共布置24个测点，其中浮动筛框8个测点，主动筛框16个测点，如图5所示。筛体上的每个测点都要测量x、y、z三个方向的响应信号，并且每个测点的每个方向都要进行三次测量，然后进行平均处理，从而消除随机误差。为了避免激励点与某一阶节点接近，且保证获取所有模态，采用多输入多输出(MIMO)的激励方式，即测试时选取点4作为激励点，对其x、y、z三个方向分别进行激励[19]，其余点为响应点。

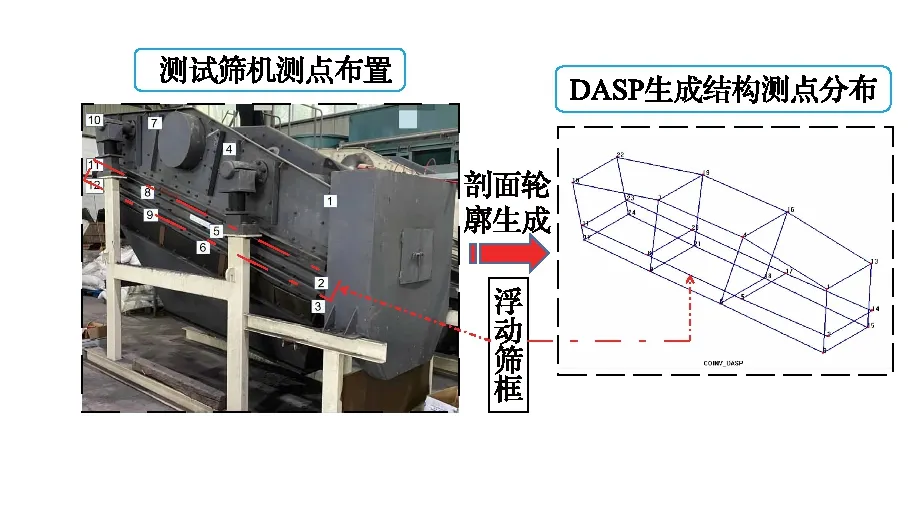
图5 测点布置

2.3.1 试验设备与测试方法

本文论述MIMO模态测试方式为激励点固定移动响应点[20]，即在固定的激励点使用力锤进行锤击试验，依次移动传感器到所有响应点，获取多组频响函数(FRF)。

实验测试中，信号采集仪采集力锤锤击筛箱激励点时对应激励力信号以及经三向加速度传感器采集并转化的振动响应数字信号，然后使用电脑对信号采集仪采集到的数字信号进行数模转换并记录。采用DASP-V10动态测试分析系统，进行激励和响应信号的采集、基本信号分析、高级信号分析以及结果输出。试验测试设备型号见表3，测试流程如图6所示。

表3 试验测试设备及型号

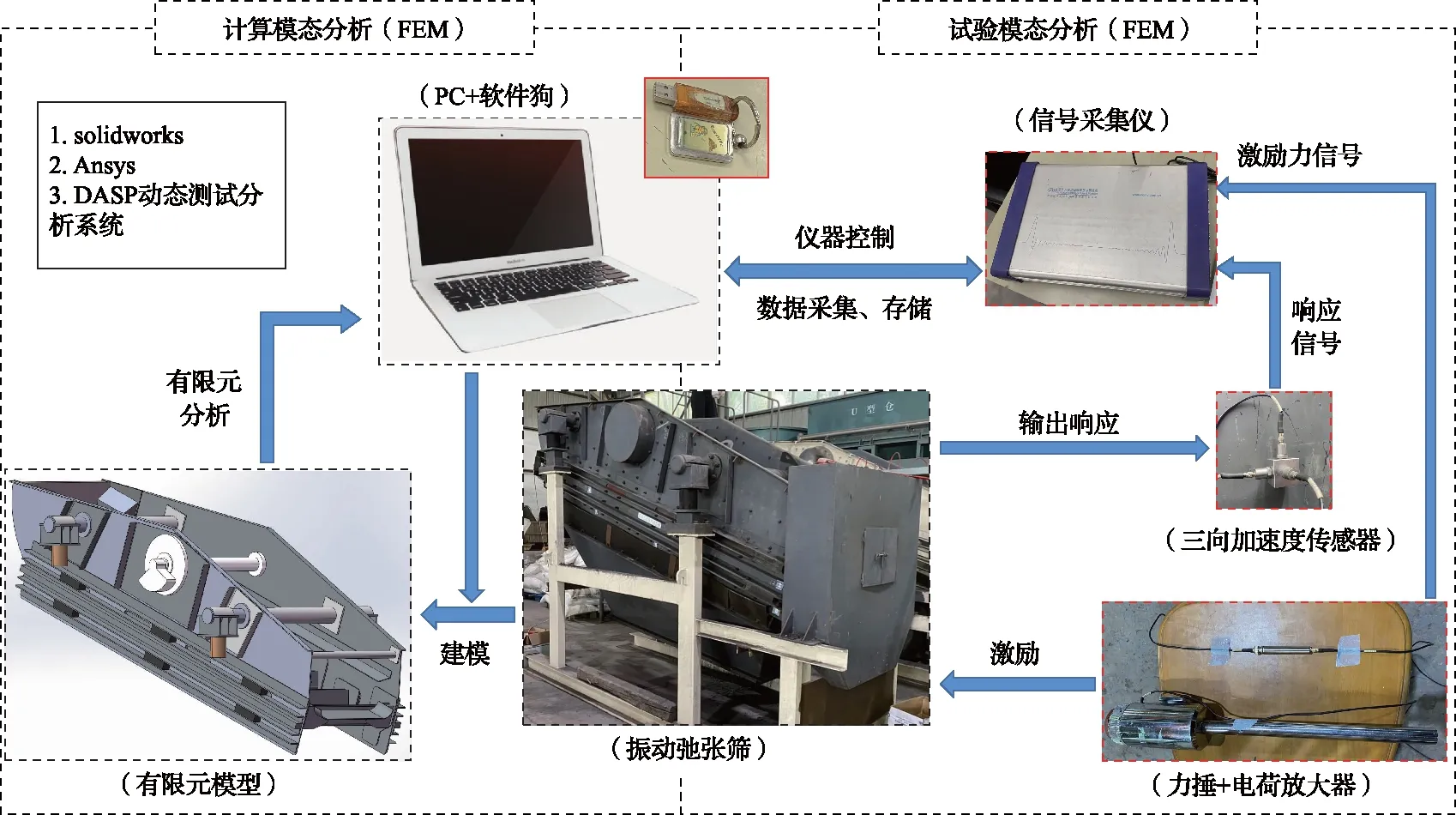
图6 试验测试流程

2.3.2 实验模态的固有频率和振型

采用DASP-V10中试验模态分析模块对现场采集得到的数据进行分析，通过FRF计算进行频响函数分析[21]，通过观察相干函数判断出激励信号与响应信号的相关性较好。采用特征系统实现算法(ERA)进行模态参数识别，在参数识别完成后，收取稳态图中稳定的“S”频率，得到前十一阶固有频率，见表4。将收取稳态图中的模态参数结果导入由试验中对应测点号建立的几何模型中，进行“质量归一”操作，得到筛机结构的前十一阶模态振型，如图7所示。

表4 前十一阶固有频率(EMA) Hz

2.4 结果对比

通过对应图4与图7中0827圆振动弛张筛各阶模态振型，发现第3阶计算模态与第2阶实验模态振型相同；第2阶计算模态在实验模态中未找到相近振型，分析其原因，由于实验过程中，筛箱底部与挡料装置有贴合，限制了筛箱沿着X方向的自由度，其次因前两阶模态数值很小且很接近，易受到测试过程中产生的噪声等因素的影响，未收到第2阶实验模态稳态参数；第7阶实验模态在计算模态中未找到相似振型，主要原因为：计算所使用的剪切弹簧材料属性认为是均匀致密的，不存在孔隙等，实际上可能是材料结构不均匀致密，给计算带来误差，导致没有第7阶计算模态参数。比较表2和表4中弛张筛各阶固有频率，综合得到筛机模态参数汇总见表5。

由表5可知，0827圆振动弛张筛前六阶的模态振型主要表现为柱状橡胶支撑弹簧形变，筛机整体沿坐标轴做平动及摆动的刚体运动；第7阶、第9阶、第10阶和第12阶模态振型表现为剪切弹簧与柱状支撑弹簧形变，主、浮筛框沿坐标轴做反向平动及摆动的刚体运动；第8阶和第11阶模态振型分别表现为浮动筛框的结构形变与筛体的结构形变。

由表5可知，两种方法获得的0827圆振动弛张筛各阶固有频率值相对误差在20%以内[22]，可以认为弛张筛刚柔耦合有限元模型的建立与边界条件的设定是合理可靠的，同时也表明对双质体振动筛进行实验模态分析的结果是准确的。本文分析的0827圆振动弛张筛工作频率为11.67Hz，筛机的工作频率在筛机第6阶固有频率与第7阶固有频率之间，工作频率避开了振动系统各阶次的固有频率，保证了筛机结构在平稳状态工作时不会因为系统共振而受到破坏。

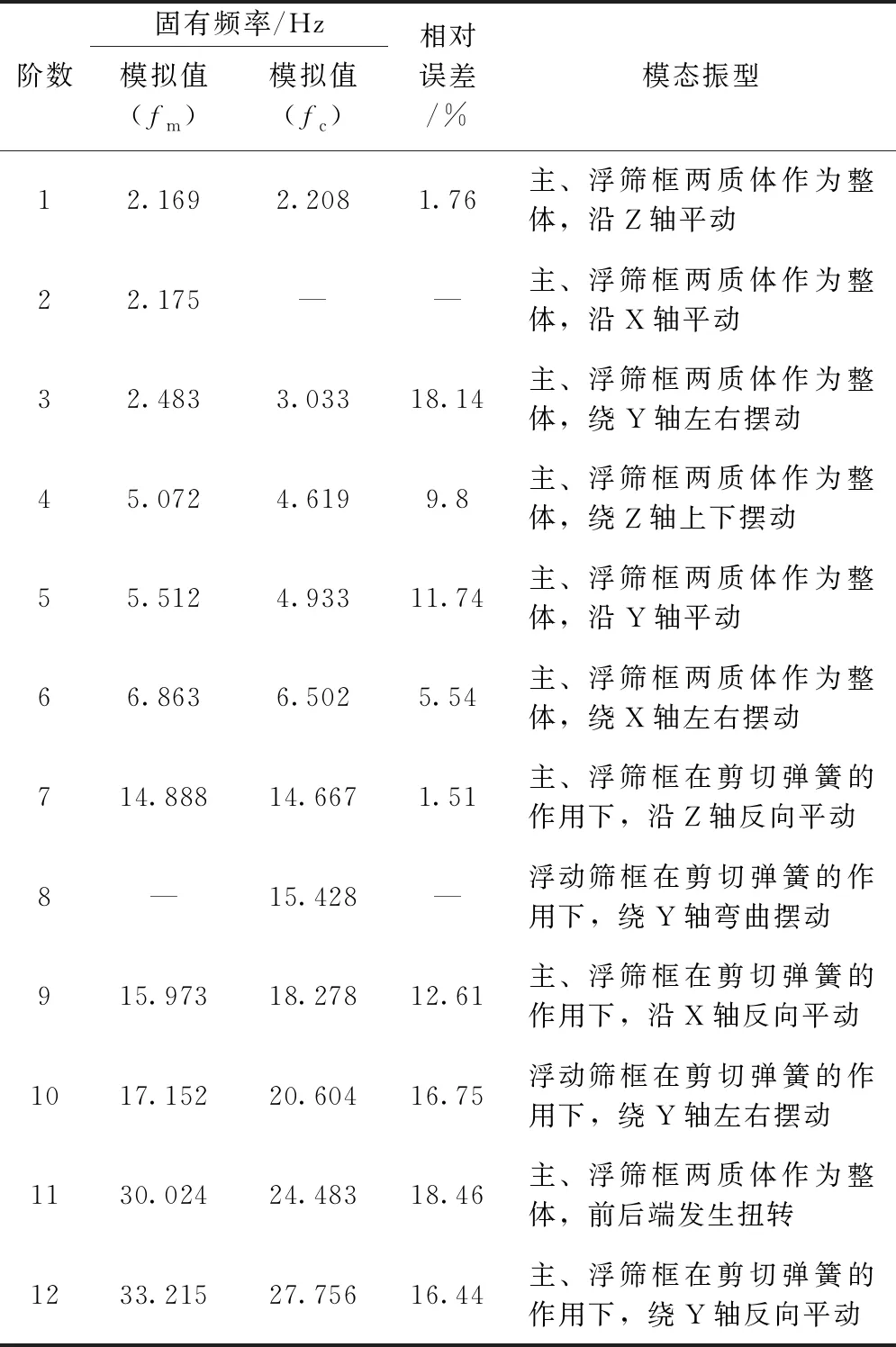
表5 两种模态分析结果对比

模态实验结果表明，圆振动弛张筛在工作频率附近有一阶浮动筛框发生弯曲变形的模态频率，其振型如图7所示，即浮动筛框以筛体质心为轴心，由上向下为轴线，发生弯曲变形，该振型会使筛面横向弹性形变增大，导致筛板易损坏，柔性筛板的弛张效果及筛分效果变差。出料端的左右位移量变大，说明浮框结构刚度较小，这对筛机结构不利，因此需要做增加剪切弹簧数量以及增加浮动梁连接槽钢部位刚度的改进。

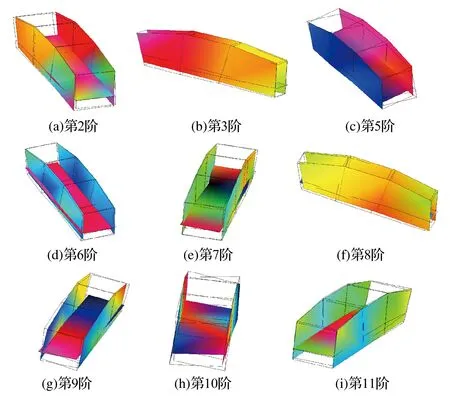
图7 1-11阶部分模态振型(EMA)

观察两种模态分析结果的振型，发现筛机第十一阶模态振型为筛体的前后端发生扭转，如图7所示。其形变主要发生在侧板上激振器安装位置附近，说明该区域结构刚度较小，因此需要采取增大该位置补强板或增加加强角钢个数的方式来进行筛机整体结构的优化。

3 结 论

1)对振动弛张筛进行计算模态分析，初步了解筛机固有频率分布范围、模态疏密程度以及各阶振型等，为模态测试实验中激励点选择、测点布置、采样频率设置等因素的确定提供依据。

2)通过两种模态分析结果证明该振动弛张筛的工作频率取值合理，位于整机刚体运动与主、浮筛框左右相互错动之间，不会引起结构的共振。圆振动弛张筛在工作频率附近有一阶浮动筛框发生弯曲变形的模态频率，根据模态叠加原理，邻近模态振型具有最大的叠加比例因子，因此可以适当增加剪切弹簧个数，同时增大浮动梁连接槽钢部位的刚度，来优化浮框的结构。

3)通过对比两种模态分析结果得到，因实验过程中，筛箱底部与挡料装置有贴合，限制了筛箱沿着X方向的自由度，其次前两阶模态数值很小且很接近，在测试过程中受到噪声等因素影响，第2阶实验模态没有测出；因计算所使用的剪切弹簧材料属性认为是均匀致密的，实际并非如此，故没有计算得到第8阶模态参数。圆振动弛张筛其余各阶固有频率值的相对误差在20%以内，总体相差不大，验证了采用有限元软件对双质体振动筛建立刚柔耦合模型进行预应力模态分析的合理性与可靠性。这种方法可以应用在设计阶段对大型弛张筛的结构进行优化、改进。