介电常数近零材料中的光与物质相互作用(特邀)
2022-06-28王衡李贵新梅霆
王衡,李贵新,梅霆
(1 西北工业大学物理科学与技术学院,西安 710129)
(2 南方科技大学材料科学与工程系,广东深圳 518055)
0 引言
材料的折射率决定了光在其中传播的基本规律。在众多新型光学材料中,零折射率材料备受关注[1]。英国科学家PENDRY J B 等在1996 年通过调控金属线的占空比,使人工结构材料的等效等离激元共振频率发生红移,从而实现了对等效介电常数从负到正的连续调控[2]。另一方面,通过设计金属开口谐振环结构的几何参数可实现负的磁导率[3]。如果介电常数和磁导率同时为负值,可实现负折射率材料[4,5]。此外,人们基于金属-介质复合结构设计并制备了在可见光波段工作的零折射率材料[6,7]。由于金属共振结构具有较高的光学损耗,会限制这类人工结构材料的实际应用。因此,人们也探索了如何使用低损耗的全介质材料实现零折射率现象。2011 年,香港科技大学的CHAN C T 等设计了具有狄拉克锥型色散特性的光子晶体结构,从而使材料表现出零折射率响应[8]。通过优化其共振单元结构,可进一步实现低损耗的折射率近零材料[9,10]。然而,这些零折射率材料都是人工结构构成的,其宏观折射率为零,但在微观尺度下折射率不为零,如果使用这些材料制造的器件的局域特征与其微结构尺寸相当,其零折射率特性则难以保证[11]。
光学材料的折射率可由相对介电常数εr和相对磁导率μr得出。零折射率材料要求介电常数和磁导率均为零,但在光频段绝大部分材料都是非磁性的,其相对磁导率μr≈1。因此,需要设计共振结构实现等效的零磁导率[12]。一些常见材料在特定波长处的介电常数实部为零,该波长被称为介电常数近零(Epsilon-near-zero,ENZ)波长。例如,透明导电氧化物在近红外波段的介电常数实部跨过零。虽然μr≈1,但由于εr近零,其折射率小于1且接近于零[13]。在ENZ波长处,折射率的实部与虚部相等,Re{n}=Im{n}=,Im{εr}越小则n越接近于0。ENZ 材料作为微纳光学领域一种重要的材料平台,近些年逐渐成为人们广泛关注的研究对象[14,15]。
在光与物质相互作用领域,如果需要利用一束光去控制另一束光,通常需要光与材料之间具有强的相互作用。近年来,人们发现透明导电氧化物具有良好的光电性能与可调谐性[16-18]。利用此类ENZ 材料,可以实现光的透射率[19,20]、反射率[21]和偏振态[22]的全光调控。这些研究表明,ENZ 材料的线性和非线性光学响应在电光调控、非线性光学频率转化和全光调控等领域具有极大应用价值[23,24]。
本文从线性和非线性光学范畴综述了介电常数近零材料中光与物质相互作用的原理与应用进展。在线性光学部分,讨论了透明导电氧化物材料的光学性质、介电常数近零模式、电调控特性等方面的内容。在非线性光学部分,讨论了介电常数近零材料在非线性折射率调控、非线性频率转换以及时变ENZ 材料中的非线性光学响应等方面的研究进展。最后,展望了介电常数近零材料领域的未来研究方向和应用领域。
1 ENZ 材料的线性光学性质
光在材料中的相速度可表示为vp=c/n=c/εr。ENZ 材料的折射率n的实部小于1,因此光在ENZ 材料中的空间相位累积小于其在真空中的空间相位累积。基于这些特性,人们从理论上研究了ENZ 材料的波导隧穿效应[25-28],波导中的完美弯曲等现象[29,30]。由于ENZ 材料具有电场屏蔽效应[31],ENZ 材料内部的空腔不影响材料的电响应。因此,通过在ENZ 材料中做磁性掺杂,有可能在介电常数缓变的情况下有效调控磁导率[32]。由于具有亚波长厚度的各向同性的ENZ 薄膜对光的电场和磁场响应的不对称性,当圆偏振的光束入射时,可以使反射光和透射光具有相反的圆偏振,并且光场携带2 阶轨道角动量量子数[33]。
其实,许多常见材料在特定波长处都存在介电常数近零现象[13],例如银(Ag)、铝(Al)等金属的ENZ 波长在紫外波段;氮化钛(TiN)、硅化钛(TiSi)等氮化物、硅化物在500~1 000 nm 波段;锗掺氮化镓(Ge:GaN)、铟掺氧化镉(In:CdO)、镝掺氧化镉(Dy:CdO)等在2.0~4.0 μm 波段。氧化铟锡(Indium Tin Oxide,ITO)、铝掺氧化锌(Aluminum doped Zinc Oxide,AZO)、镓掺氧化锌(Gallium doped Zinc Oxide,GZO)、氟掺氧化锡(Fluorine doped Tin Oxide,FTO)等透明导电氧化物的ENZ 波长通常在1 100~2 000 nm 的近红外波段[16,18,34],覆盖两个通信波段。透明导电氧化物的费米能级位于导带内,载流子密度通常在1020~1021cm-3量级,因而具有较好的导电性。另一方面,大多数透明导电氧化物的带隙较大,通常大于可见光光子能量,因此对可见光的吸收较小[17,35]。通过改变这类材料中的载流子密度、电导率、等离子体频率等参数,可实现透明导电氧化物的良好可调谐性。基于这些优良特性,透明导电氧化物在逐渐成为备受欢迎的光学材料[15,36,37]。透明导电氧化物在ENZ 波段的相对介电常数可以使用Drude 模型描述

式中,ω为光的角频率,ε∞为高频介电常数,ωp为等离子体频率,γ为弛豫系数,如图1。求解Re{εr(ω)}=0可得其ENZ 频率为
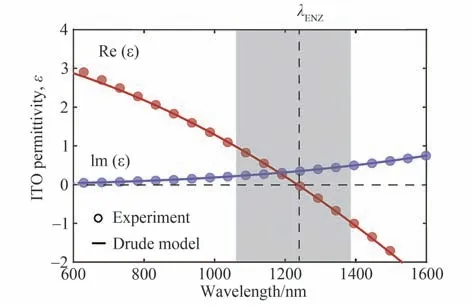
图1 ITO 介电常数的测量值和Drude 模型理论曲线,实部等于0 的波长为ENZ 波长[21]Fig.1 Measured permittivity of ITO and theoretical curve of the Drude model,the wavelength where the real part equals 0 is the ENZ wavelength[21]
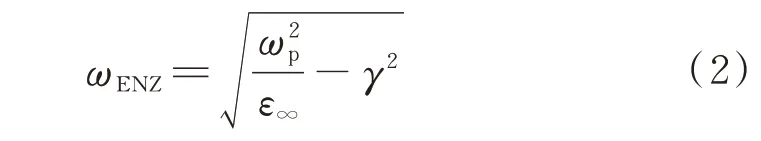
在倾斜入射的情况下,ENZ 薄膜样品在ENZ 波长处存在一个吸收峰。根据这一特性,可以很容易确定材料的ENZ 波长[38]。
作为一类掺杂氧化物半导体,掺杂浓度与晶态对透明导电氧化物的ENZ 波长有重要影响。使用磁控溅射制备ITO 薄膜时,通过改变工艺参数可以调控掺杂浓度[39-41]。 在使用原子层沉积(Atomic Layer Deposition,ALD)制备AZO 时,改变原子层比例来调控掺杂浓度,进而可以调控ENZ 波长[42,43]。在沉积后,也可以用热退火的方式调控ENZ 波长。这一过程中存在两个主要的竞争机制:晶粒尺寸增大导致ENZ 波长蓝移[44],以及氧注入填补氧空位导致ENZ 波长红移[45]。ITO 材料的退火阈值温度较低,在低温条件下透明导电氧化物的电学与光学性质易于调控[46],但温度调控存在调制速度慢的问题。
此外,金属和介质的多层人工结构同样可以产生等效的ENZ 响应。例如,使用Ag 和TiN 层叠薄膜[47]或者Ag 和二氧化硅(SiO2)层叠薄膜[48],可获得等效ENZ 波长处于可见光波段的双曲超构材料[49]。根据等效介质模型,其纵向和横向的介电常数可写为

式中,εm和εd分别为金属和介质的介电常数,dm和dd分别为金属和介质的厚度。可以看出,双曲超构材料是一种各向异性材料,沿不同方向的介电常数不同,通常只有纵向的介电常数ε⊥近零[50]。与人工零折射率材料类似,双曲超构材料的等效ENZ 也是一种宏观效应。
在不考虑面电流和面电荷的情况下,由麦克斯韦方程可得电磁场矢量在材料界面处的边界条件。其中电位移矢量的垂直分量连续D1n=D2n,即ε1E1n=ε2E2n,电场矢量的切向分量连续E1t=E2t,磁感应强度的垂直分量连续B1n=B2n,即μ1H1n=μ2H2n,磁场强度的切向分量连续H1t=H2t。在界面处求解电磁波波方程可以得到界面模式,其中金属-介质界面处支持表面等离极化激元(Surface Plasmon-polariton,SPP)模式。对于介质-金属-介质三种材料构成的双界面结构,当中间层的厚度d越来越薄时,两个界面上的模式会发生耦合劈裂,形成长程SPP 和短程SPP 模式,其中长程SPP 模式的色散关系满足:
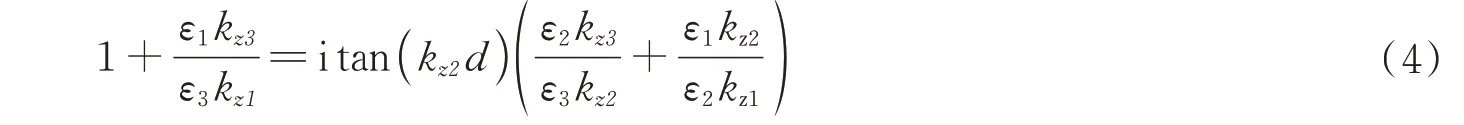
式中,ε为材料的介电常数,kz为光波矢的垂直分量。当薄膜厚度远小于波长时,长程SPP 模式色散曲线趋于平坦且接近ENZ 频率,该模式被称为ENZ 模式[51-53],如图2。ENZ 模式的电场局域在薄膜中且有较大增强,并且薄膜越薄,电场增强越大[53,54]。与激发SPP 模式类似,为了激发ENZ 模式也需要入射光的波矢满足匹配条件,传统的做法是使用棱镜或光栅实现波矢匹配。如果在超薄ENZ 基底上制备金属或介质纳米结构,那么基底的ENZ 模式会与金属纳米结构的局域表面等离激元共振模式发生耦合[55-63]。
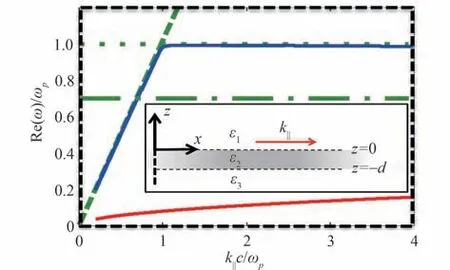
图2 超薄ENZ 薄膜中长程SPP 模式(ENZ 模式,蓝色)与短程SPP 模式(红色)的色散曲线[53]Fig.2 Dispersion relations of the long-range SPP mode(ENZ mode,blue)and short-range SPP mode(red)in the ultrathin ENZ film[53]
透明导电氧化物具有非常好的电光调控能力[17]。2010 年,ATWATER H A 等设计ITO-介质-金电容结构,通过施加电压使得ITO 界面处的载流子密度增加一个数量级。在这一过程中,ITO 的折射率改变量大于1,同时ITO 的ENZ 波长发生明显的蓝移[64],如图3(a)。基于该原理,人们设计了电调控光栅超构表面结构,可实现对光的反射相位、强度以及方向的综合调控[65-67]。可以预见,通过电调控ENZ 基底的折射率,也可以调控ENZ 模式与纳米结构的共振模式耦合效应[66,68]。
在光波导应用场景下,光的能量倾向于在高折射率介质中传播。因此,ENZ 材料本身通常不单独用作波导材料。为了充分利用ENZ 材料的电可调谐性,可以将其包裹在高折射率的波导上,通过电调控[69,70]或光调控[71]的方法改变ENZ 材料的折射率来调控波导中光的传播特性,如图3(b)。如果想使用ENZ 材料作为波导材料,则可以设计槽型波导结构。例如,使用高折射率材料包裹ENZ 材料,并将器件置于低折射率环境中,电磁波可以在槽型波导中形成稳定的传播模式[72]。类似的,也可以在ENZ 槽型波导周围的ENZ 材料中引入电调控的方法来改变光波导的传播性质[73,74]。
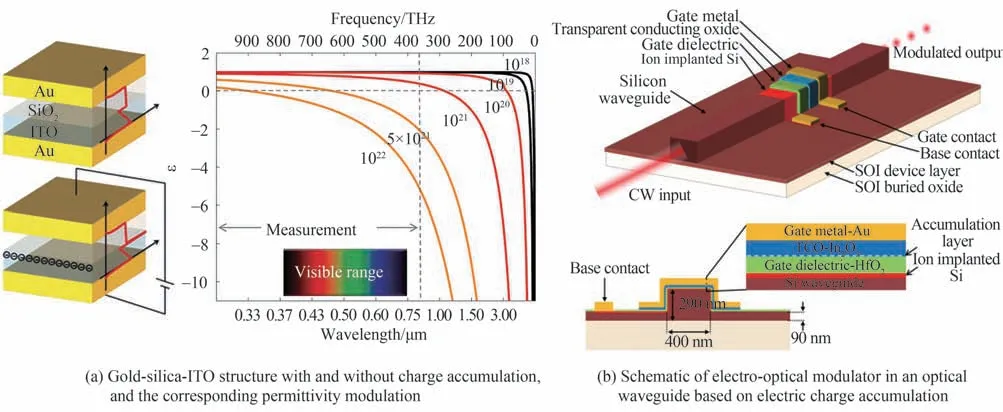
图3 ENZ 材料中基于电致电荷积累的光学性能调控[64]及其在电光调控波导中的应用[70]Fig.3 Optical modulation of ENZ material based on the electro-induced charge accumulation[64]and its application in electrooptical modulation waveguides[70]
2 ENZ 材料的非线性光学性质
在ENZ 材料中,主要有三种增强非线性光学响应的机制:
1)电场反比增强效应:根据电位移矢量在界面处的连续性条件可知E2n=ε1E1n/ε2,即电场的垂直分量反比于介电常数。因此,当倾斜入射的光的电场平行于入射平面时,ENZ 材料中光的电场强度将会极大地增强[21],因此,这一现象可以增强ENZ 材料的非线性光学响应。
2)折射率改变量反比增强效应:在材料的介电常数接近零时,其εr改变Δεr,将导致其折射率的变化量为。可以看出,当介电常数近零时,介电常数微小的改变会导致折射率很大的改变。因此ENZ 材料可以用于增大Kerr 非线性光学响应。
3)零相位匹配:在多波非线性耦合过程中,相位匹配决定了非线性光学过程的转化效率[75]。如果一个材料在对应频率的折射率或者介电常数接近零,则更容易实现非线性过程中的相位匹配条件[76]。
2.1 类Kerr 效应
透明导电氧化物在ENZ 波段的光致折射率改变主要起源于热电子动态过程,导带内的电子能态密度重新分布导致材料的折射率变化。需要指出的是,ENZ 材料的折射率较低,并且在非线性光学过程中折射率改变量较大。因此,传统非线性光学中基于微扰近似得出的n=n0+n2I不再适用,可以使用非线性极化率模型来描述折射率随泵浦光强的变化规律[23,77]

在ENZ 材料的非线性光学过程中,ENZ 波长对应的光子能量通常小于材料的带隙,因此只能激发导带内电子发生带内跃迁,电子密度N不变。在准热平衡近似下,电子能态密度分布可以使用Fermi-Dirac 函数描述。由于导带为非抛物线型,不同能量的电子具有不同的等效质量。因此,根据电子能态密度分布可以定义电子的整体有效质量m*[78]。不同能量的电子具有不同的散射时间,这取决于离子化杂质散射和声学声子散射等多种机制的贡献,可以根据电子能量密度分布定义电子的整体散射时间τ[79]。在ENZ 材料的非线性光学过程中,电子能态密度重新分布,导致m*和τ改变,进而导致等离子体频率和弛豫系数的改变。
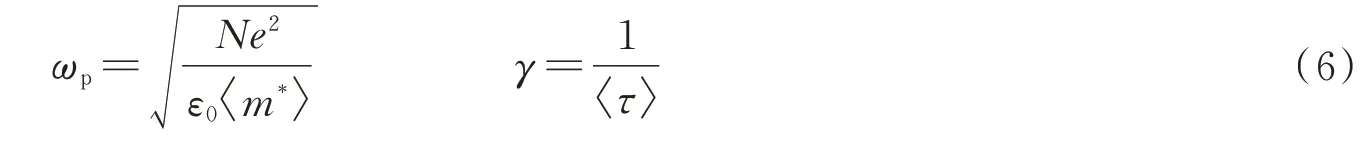
根据Drude 模型,可求得介电常数εr并可以进一步计算出非线性折射率n。n的实部变化对应于非线性光学折射,虚部变化对应于非线性光学吸收[80,81]。当然,ENZ 材料中也存在非线性极化导致的非线性光学Kerr 效应,但比热电子非线性光学效应小几个数量级[82],因此一般被忽略。值得注意的是,双能级系统近似下的四波混频模型[82]未能明确处理带内电子特性,因此难以准确描述ENZ 材料的非线性光学响应。在ENZ 材料中,电子带间跃迁产生的非线性光学响应往往与带内跃迁产生的非线性光学响应相反。例如,带内跃迁导致透射率增加而带间跃迁导致透射率减小[83],这主要是因为带内跃迁导致电子整体有效质量m*增加,而带间跃迁导致电子密度N增加,两者对等离子体频率ωp的影响是相反的。
由于ENZ 材料具有很强的非线性光学响应,因此使用ITO[21]或AZO[84,85]等材料制备的薄膜可实现对光的透射率与反射率的全光调控。除此之外,还可以对光的偏振态[22](如图4(a))和薄膜的等离激元共振模式实现全光调控[86]。如果将ENZ 材料制成纳米柱阵列[19,87,88](如图4(b))或纳米小球[80]时,由于等离激元共振增强效应,非线性光学响应相比于垂直入射时有极大增强。这一现象的本质是入射光场被纳米结构散射,从而产生了垂直于ENZ 材料界面的电场分量,进而产生电场增强。此外,将ENZ 材料置于共振腔内,通过泵浦调控ENZ 材料的光学性质,可以实现对腔的共振波长的调控[89]。在ENZ 薄膜上制备金属共振结构,基于等离激元共振与ENZ 模式的共振耦合,可以进一步增强非线性光学响应[20](如图4(c))。
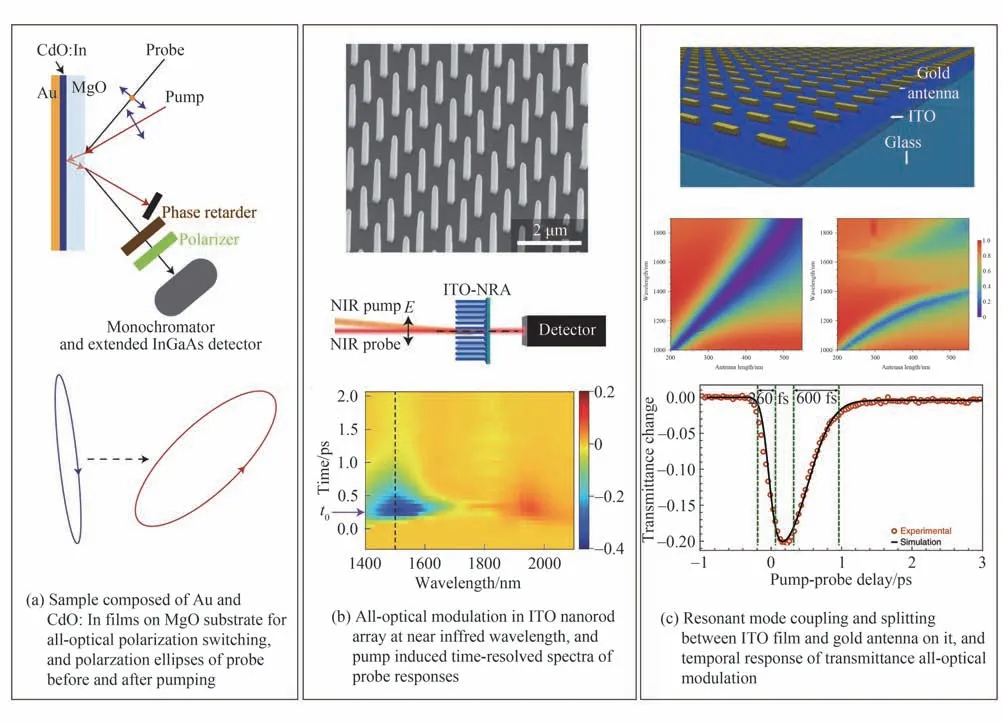
图4 ENZ 光学器件中偏振态[22]和透射率[19,20]的全光调控Fig.4 All-optical modulation of polarization state[22]and transmittance[19,20]in ENZ photonic devices
2.2 非线性混频过程
谐波的产生是非线性光学中一类重要的现象,人们在ENZ 材料中也实现了谐波发射的增强效应,如图5(a)。对于二次谐波产生来说,通常需要非线性材料具有中心反演对称破缺特性。如同在其他材料中一样,ENZ 材料界面处存在对称性破缺可导致二次谐波的产生[90],与此同时,ENZ 材料中的电场增强效应、洛伦兹力和电四极贡献都可进一步增强二阶非线性光学效应[91-93]。如果设计人工结构材料使其等效介电常数在基频和二次谐波频率均为0,可实现零相位匹配的强二次谐波产生[94]。除此之外,也可以使用金属超构表面的等离激元共振模式来增强ENZ 薄膜中的二次谐波产生。例如,设计在基频共振的金属纳米棒并将ENZ 波长设置于倍频波长[95];使用金属纳米光腔的间隙模式[96]或超构单元的等离激元共振模式与ENZ 模式耦合[97];或者将介质共振结构置于ENZ 薄膜上[98],均可实现二次谐波效率的增强,如图5(b)~(c)。此外,在近红外波段的飞秒激光泵浦下,可以在低损耗的ENZ 材料中观测到三次、五次、七次和九次谐波的产生[99-102],如图5(d)。当激发功率进一步提升,基频光和这些高次谐波在材料内发生自相位调制、三波混频、四波混频、拉曼散射等非线性光学过程,可使得发射频谱进一步展宽[103]。除此之外,ENZ 材料在飞秒激光泵浦下,还可以通过光整流效应发射太赫兹波[104],当薄膜的ENZ 模式与金属超构单元的等离激元共振模式耦合时,太赫兹波的产生效率会得到进一步增强[105,106]。
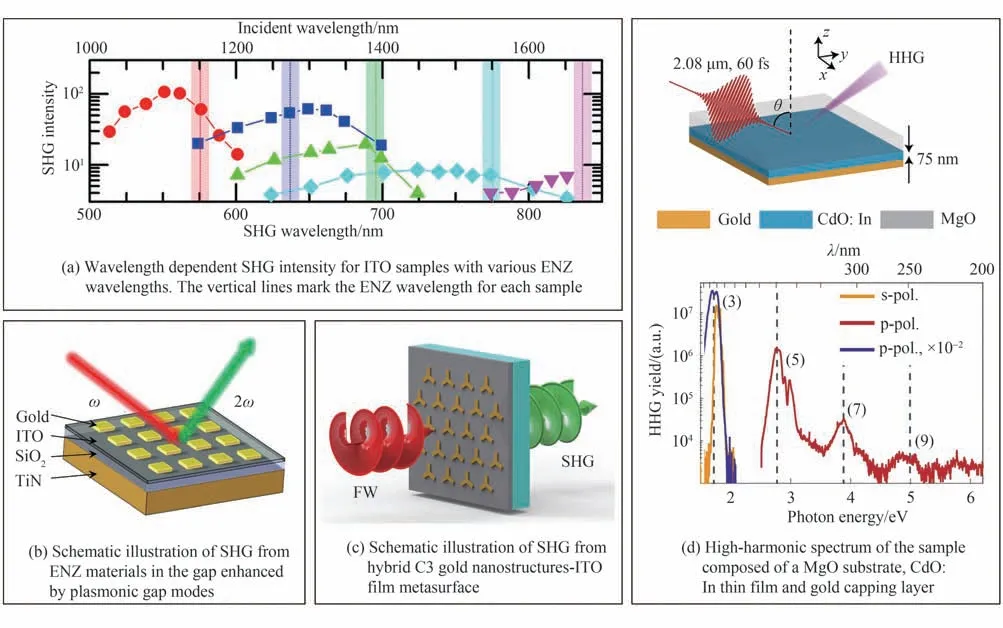
图5 ENZ 材料和ENZ-金属复合结构中的非线性光学频率转换[93,96,97,101]Fig.5 Nonlinear frequency conversion in ENZ materials and ENZ-metal hybrid devices[93,96,97,101]
2.3 时变ENZ 材料中的非线性光学响应
在ENZ 材料的非线性光学过程中,材料的折射率在几百飞秒内快速变化。在此过程中,在材料中传播的光将会产生频移[107-109]。在光泵浦时,ENZ 材料的折射率增大,其中探测光的频率减小,发生红移。在材料响应弛豫阶段,折射率减小,其中探测光的频率增大,发生蓝移[110,111],如图6(a)。通过在ENZ 薄膜上制备金属纳米结构形成金属-ENZ 复合超构材料,也可产生类似的频移现象[112,113]。后续研究发现,频移不仅起源于ENZ 材料内部,还同时来源于随时间变化的空间边界条件[114]。此外,时变的ENZ 材料可用于产生相位共轭和非线性负折射效应[115,116],如图6(b)。
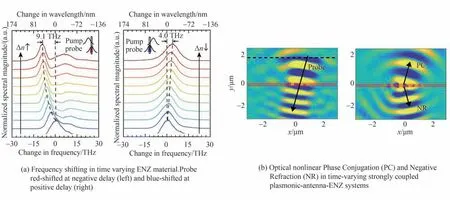
图6 时变ENZ 材料中的光学频移[110],以及时变ENZ-金属复合结构中的非线性相位共轭和负折射[116]Fig.6 Optical frequency shifting in time-varying ENZ materials[110],and nonlinear phase conjugation and negative refraction in time varying ENZ-metal hybrid structure[116]
3 总结与展望
近年来,介电常数近零材料领域的研究获得了广泛关注。这类材料中光与物质相互作用过程具有丰富的物理机制,为设计新型的光学功能器件提供了很好的材料体系。在ENZ 波段,这类材料的一个天然的劣势是其折射率低,导致光不易被局域在ENZ 材料内部。目前,人们的主要思路是将ENZ 薄膜与超构表面共振结构相结合,通过共振模式之间的耦合提升器件的非线性光学效率。在ENZ 材料的非线性光学过程中,材料的折射率改变非常大,然而所需的泵浦光强也非常高,从而限制了相关物理机制的实际应用。如何进一步提升器件的非线性光学效率,是介电常数近零光学器件走向应用所必须克服的问题。总体而言,ENZ 材料中丰富的光与物质相互作用机制有望在显示、全光信息处理等领域取得重要应用。
