基于小波理论的近场地震动模拟方法分析
2022-06-27丁庆灯
丁庆灯
(兰州交通大学 土木工程学院,甘肃 兰州 730070)
当前有限的实测近场地震动数量以及震源环境和场地条件对结构抗震的限制,引起了抗震工作者对脉冲型地震的模拟持续关注[1-2]。对实测地震动模拟的脉冲模型,学者所采用的数学模型主要有三角形模型、三角函数模型、带包络函数的三角函数模型、小波模型等模型。Mavroeidis和Papageorgiou[3]以Gabor小波为基础,通过简单的数学拟合方法提出一种单驼峰的速度时程脉冲模型;Baker[4]以多贝西小波为窗函数通过小波变换提出单驼峰的速度脉冲模型;蒲武川等[5]在Makris的模型基础上考虑地震动不同位移恢复度的情况,提出了改进的三角函数模型。除此之外也有以确定地震动为基础的地震动模拟的研究,谢俊举等[6]对汶川地震近场地震动脉冲特性进行了研究,谢礼立等[7]对唐山地震进行了模拟。
目前对近场地震动的模拟都以速度时程为基础,这样减少了高频成分对模拟结果稳定性的影响,但Rodríguez 和 Miranda[8]研究发现地震动高频成分对结构响应有一定影响,尤其对加速度需求敏感性较强。同时,近场地震动模拟均只考虑了单脉冲模型,但不少实测地震动记录含有多个脉冲,使得单脉冲模型的能量相较于实测地震动记录有很大损失。
基于单脉冲模型的不足,本文提出以多贝西小波为小波基对地震动加速度时程多次连续小波变换后模拟地震动的方法,该方法可模拟多个脉冲部分的脉冲模型且不会影响单脉冲型地震动的模拟精度。同时,选取目前几种常规单脉冲型数学模拟模型,从速度时程、反应谱和桥梁的非线性地震响应结果3个方面展开分析,对比分析各模型对不同类型地震动的模拟精度。
1 脉冲模型
1.1 包络三角函数法
带包络曲线的三角函数拟合法(Menun模型)由Menun和Fu提出,通过2段带包络线的三角函数模拟脉冲部分[9]。MF模型含有VP、TP、t0、n1和n25个参数,n1、n2为分别控制前后2段三角函数形状的参数,速度模拟公式为
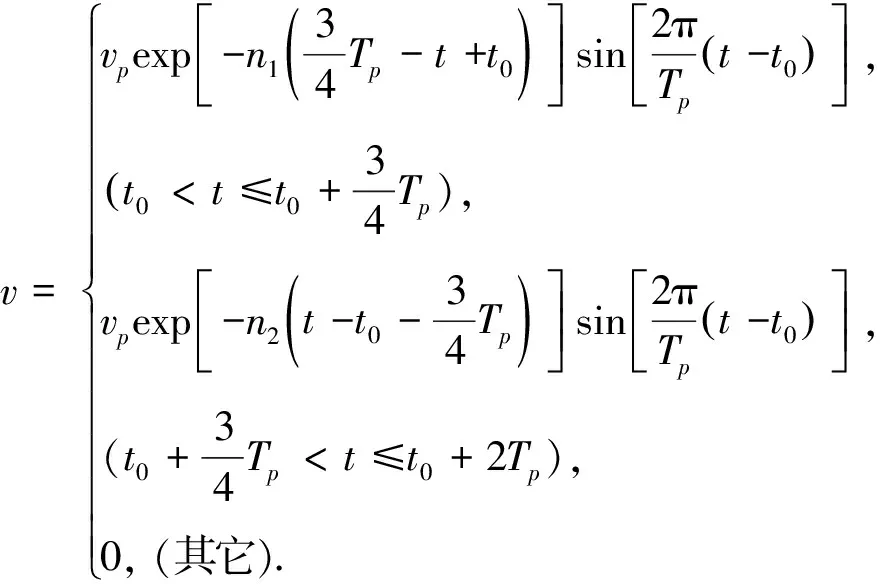
(1)
1.2 Mavroeidis模型
Mavroeidis和Papageorgiou提出了基于Gabor小波提取速度脉冲的方法(MP模型),该模型中保留Gabor小波谐波振荡部分,替换高斯包络函数为余弦包络函数[3]。MP模型包含4个参数VP、fP、γ和φ,γ控制包络线周期,φ确定振荡函数相位,速度脉冲的振动频率用伪速度反应谱峰值法并计算后求得,其他参数用试错法拟合。速度脉冲表达式为
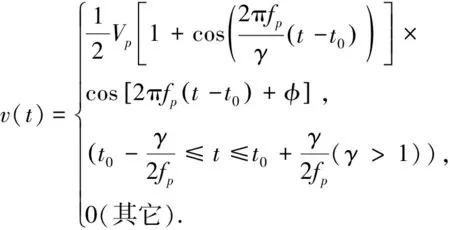
(2)
1.3 Baker模型
Baker利用4阶多贝西进行连续小波变换,对地震动速度时程信号进行频谱分析,通过连续小波变换时频图最大能量所对应的时刻和频率来确定脉冲周期和脉冲发生时间[4]。
1.4 蒲武川模型
蒲武川根据Makris的三角函数模型考虑速度峰值的正负向差异,对Makris的三角函数脉冲模型作出改进,使模型能够模拟不同永久位移的地震动[5]。该模型(PWC模型)包含正负向速度时程峰值vm+、vm-;位移时程峰值dm;脉冲周期TP。速度模拟及脉冲周期公式为
(3)
(4)
2 本文拟合方法
地震波属于典型的非平稳信号,频域特性随时间变化而变化。对于局部区域的频谱特性傅里叶变换不能实现,类似于窗口函数的小波变换在非平稳信号中有明显的优势,能反映地震波的局部频谱特性。小波变换表达式如式(5)所示,通过改变幅值a和窗函数时间t来实现。
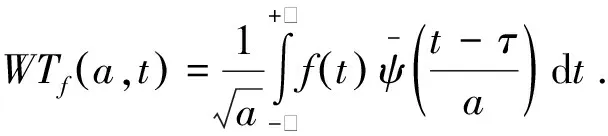
(5)
Baker模型中仅得到单脉冲模型,对近断层地震动中高频成分和多脉冲部分的模拟有很大局限性。前几种模型都以地震动速度时程为研究对象,虽然能简化拟合的难度,但是经过对比发现,用速度时程曲线作为拟合对象会丢失地震动加速度时程曲线的很多特性,尤其是加速度多脉冲时程。基于此,本文以加速度时程曲线为研究对象,利用多次小波变换来模拟多脉冲地震动以提高拟合精确度。
本文先通过MATLAB对地震动加速度时程进行连续小波变换,然后获得频谱图中最大能量值所处位置,根据小波变换尺度数组查找并确定对应幅值a,脉冲周期T计算公式为
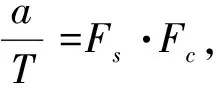
(6)
式中:Fs为采样频率;Fc为小波中心频率。
根据对地震波的观察发现,大多地震波的脉冲次数在4次以下,本文经过4次拟合得到多脉冲模型,速度脉冲周期取多脉冲模型最优频率所对应的周期。
3 地震动模拟
3.1 地震波选取
本文中为尽可能确保各模拟方法保持原文的准确性,从Mavroeidis模型所提供的近场地震时程中根据Baker所提出的脉冲指示公式筛选出8条地震波(见表1),所选地震波均为与断层向垂直的波分量。选取的8条地震波按典型特征又分为了3类:1、2、3号地震波为典型单脉冲型地震波;4、5、6号地震波为多脉冲型地震波;7、8号地震波为长周期脉冲型地震波。
3.2 地震动速度时程曲线拟合
Menun模型实际模拟过程中,按原文所述先用遗传法得到5个参数的局部最优值,然后用牛顿法求出整体最优值。蒲武川模型原文中未给出脉冲初始时刻的求值方法,实际模拟过程中用脉冲地震动与原始地震动最小标准差的方法求得,脉冲周期取Baker模型的周期,其余参数按原文所述求得。其他模型均按原文方法模拟。本文模型以加速度时程为参考拟合后转化为速度时程曲线,地震动速度时程曲线拟合结果见图1。

表1 地震波基本信息
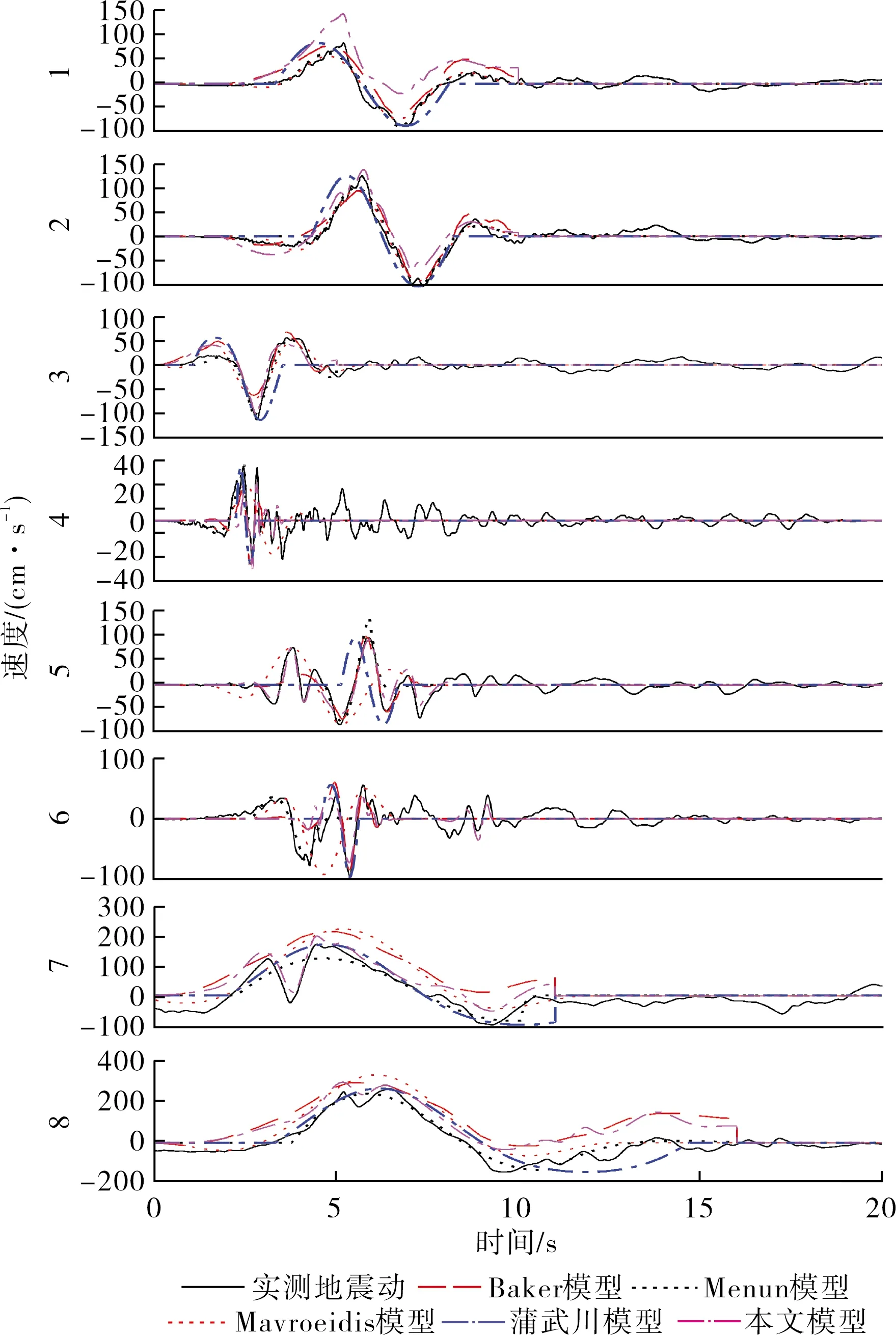
图1 速度时程曲线
由图1可看出:不同的地震波、不同的模拟方法结果有一定偏差,部分能与原地震动很好吻合,也有部分拟合出现较大偏差。其中:1、2、3号地震波各拟合方法均较好,但是蒲武川模型因其模型的缺陷使得最后一个小脉冲无法拟合;4、5、6号地震波为多脉冲地震波并含有大量高频成分,而上述拟合方法中单脉冲模型均只能拟合有限数量脉冲,故整体拟合结果不够理想,同时多脉冲的缘故使得各单脉冲模型识别出不同的主脉冲而导致脉冲周期也因拟合方法不同而明显不同,本文模型则对多脉冲型地震动的模拟效果则明显提升,能有效模拟多个脉冲;7、8号地震波的拟合中Baker和Mavroeidis模型的拟合地震波整体略大于原始地震波,其余单脉冲模型仅能较好拟合主脉冲,但多脉冲模型则能很好拟合出主脉冲中的次要脉冲。
不同拟合方法所得拟合结果的地震特征参数见表2。由表2可知:不同模型的单脉冲地震动和长周期地震动脉冲周期结果相近,偏差很小;4、5、6号多脉冲周期地震动不同模型的脉冲周期偏差较大,如6号波MF模型周期TP=6.45 s,而Baker模型周期TP=1.04 s,这主要是本文所列举的脉冲模型均只考虑单一脉冲,对多脉冲模型的拟合没有一定的准确性。
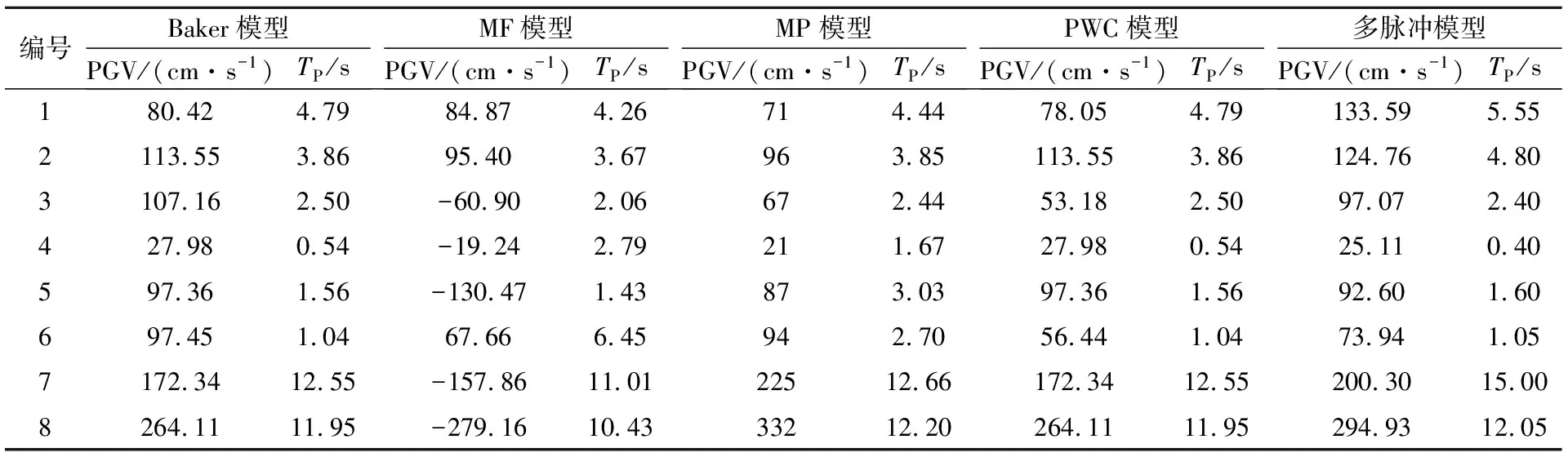
表2 各模型模拟结果
3.3 反应谱分析
将每条地震动不同模拟方法的反应谱与原地震动的反应谱结果对比,分别计算阻尼比为5%、10%、30%三种情况下相对速度反应谱的结果。图2反映了阻尼比分别取5%、10%、30%时不同地震动拟合波与原波的反应谱表现。
由图2可以看出:在高自振频率内,所有实测地震动的反应谱曲线明显高于其单脉冲拟合地震动反应谱曲线,随着自振频率降低两者逐渐相吻合;相较于单脉冲模型,本文模型拟合地震动与实测地震动的反应谱相比,在高自振频率和低自振频率段均有良好的吻合度,较单脉冲模型在低自振周期有明显优化。这种现象主要由多个原因导致,对单脉冲型地震动而言,本文模型因有多次拟合过程,能有效拟合部分含有较高能量的高频成分;对多脉冲型地震动而言,模拟多个脉冲使得更多脉冲被识别;对于长周期地震动而言,能有效识别主脉冲中的次要脉冲而有效提高地震动整体的拟合度。对于不同单脉冲模型的结果也会出现局部大偏差,如Mavroeidis模型对多脉冲模型的模拟在实测地震动卓越周期出现后有很大偏差,所有单脉冲模型对长周期地震动的模拟在实测地震动卓越周期出现后几秒内也有很大偏差。同时随着阻尼比增加,高自振频率部分的峰值减少,反应谱曲线更光滑。
为显示模拟结果的直观性,图3反映了各模拟地震动与原始地震动相对位移反应谱的比值,模拟结果与图2所表现的基本一致,单脉冲模型模拟的单脉冲型和长周期型地震动的反应谱在短自振周期内出现很大差异,长自振周期阶段则吻合度较高,而本文模型则对整个阶段均表现良好。单脉冲模型对多脉冲型地震动的整个阶段模拟结果很差,Mavroeidis模型模拟结果明显高于实测地震动反应谱,而其他模型则低于实测地震动反应谱。本文模型则对4、6号波的反应谱表现较差,对5号波的反应谱表现良好,这可能是4、6号波多脉冲不够显现的原因,但本文模型整体较单脉冲模型的结果有提升。
由图2~3可知:多脉冲模型的拟合结果相较于单脉冲模型拟合地震动的反应谱结果有明显提升;对单脉冲型地震动可提升高自振频率段内反应谱的拟合度;对多脉冲型地震动可以优化整体反应谱吻合度;对长周期型地震动可提高反应谱高中自振频率段吻合度。
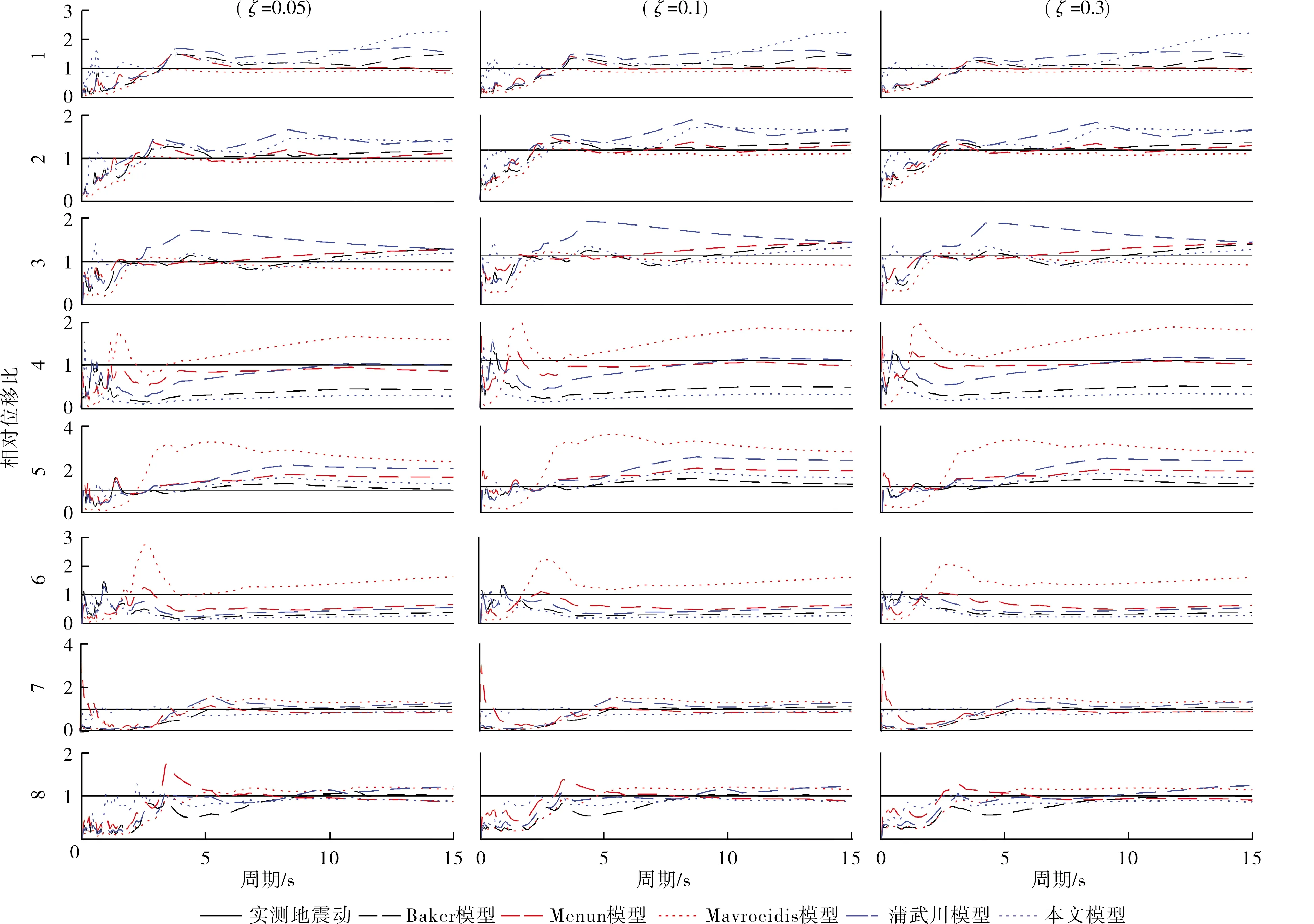
图3 相对位移反应谱比
4 桥梁结构响应分析
4.1 有限元模型的建立
本文所选桥梁为某铁路4跨连续梁桥(72+2×120+72) m,该桥位于Ⅱ类场地,抗震设防级别8度,地震动峰值加速度0.3g。本桥桥面宽12.2 m,上部为变截面单箱单室C55混凝土现浇结构,下部结构采用重力式桥墩,边墩为C40混凝土材料,中墩为C50混凝土材料。承台材料为C30混凝土,桩基础材料为C35混凝土。
本文基于CSi Bridge有限元分析模块建立桥梁非线性有限元模型,主梁用弹性梁单元模拟,摩擦摆支座采用系统自带的Friction Isolator单元模拟,桥墩采用弹塑性梁柱单元模拟,从左往右编号依次为1#~5#桥墩。在本文材料本构模型模拟中,钢筋用软件自有的Simple模型模拟,混凝土用Mander本构模拟。构件所选滞回曲线的准确性对时程响应结果的精确性有决定性作用,选择合理的滞回模型很有必要,简单的模型影响结果的准确性,复杂的模型又会影响计算效率,因此本文使用考虑刚度退化的武田双折线模型。全桥的有限元模型见图4。
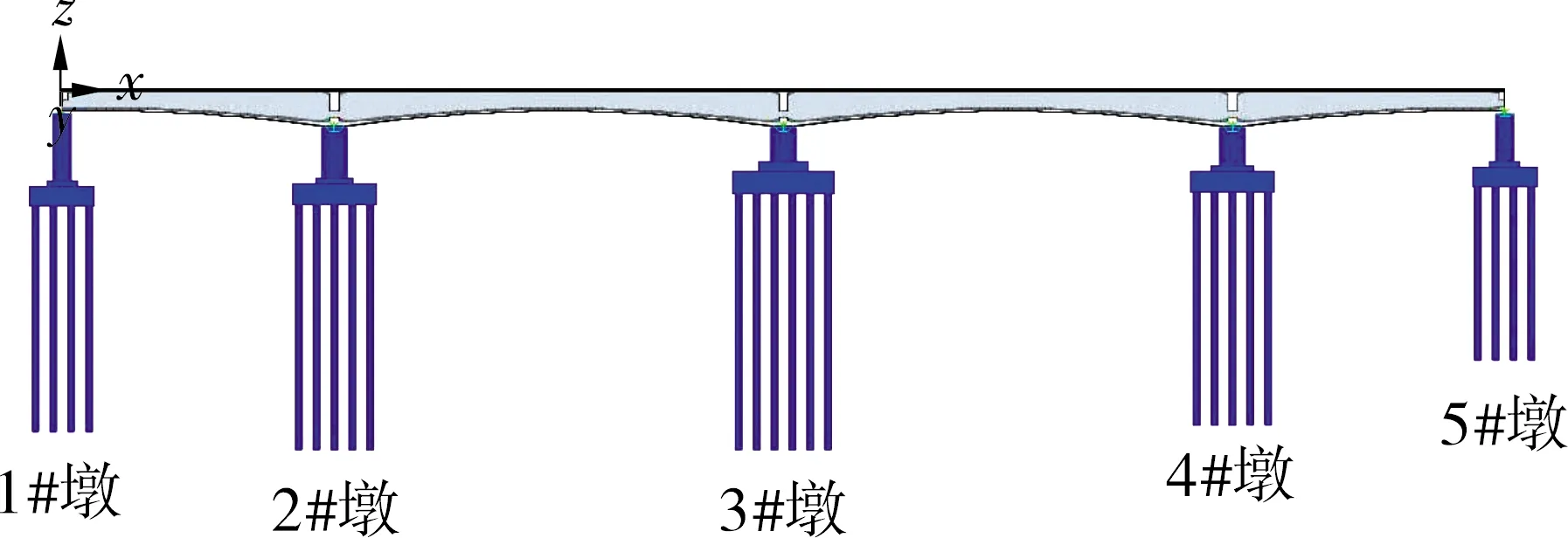
图4 全桥有限元模型
4.2 非线性时程分析结果
时程分析会因地震波峰值加速度PGA不同有明显差异,为减小不同地震动PGA对时程结果分析的影响,将原始地震动幅值均调整为0.3g,对应的拟合地震动按相应比例调幅。经过对时程响应结果的查看,各桥墩的地震响应结果规律相近,为便于比较,本文以2#墩为分析对象作对比分析。图5显示了不同地震动作用下2#墩墩底最大弯矩值,图6显示了不同地震动作用下2#墩墩底最大剪力值,图7显示了不同地震动作用下2#墩墩顶最大位移值。

图5 2#墩墩底最大弯矩值

图6 2#墩墩底最大剪力值
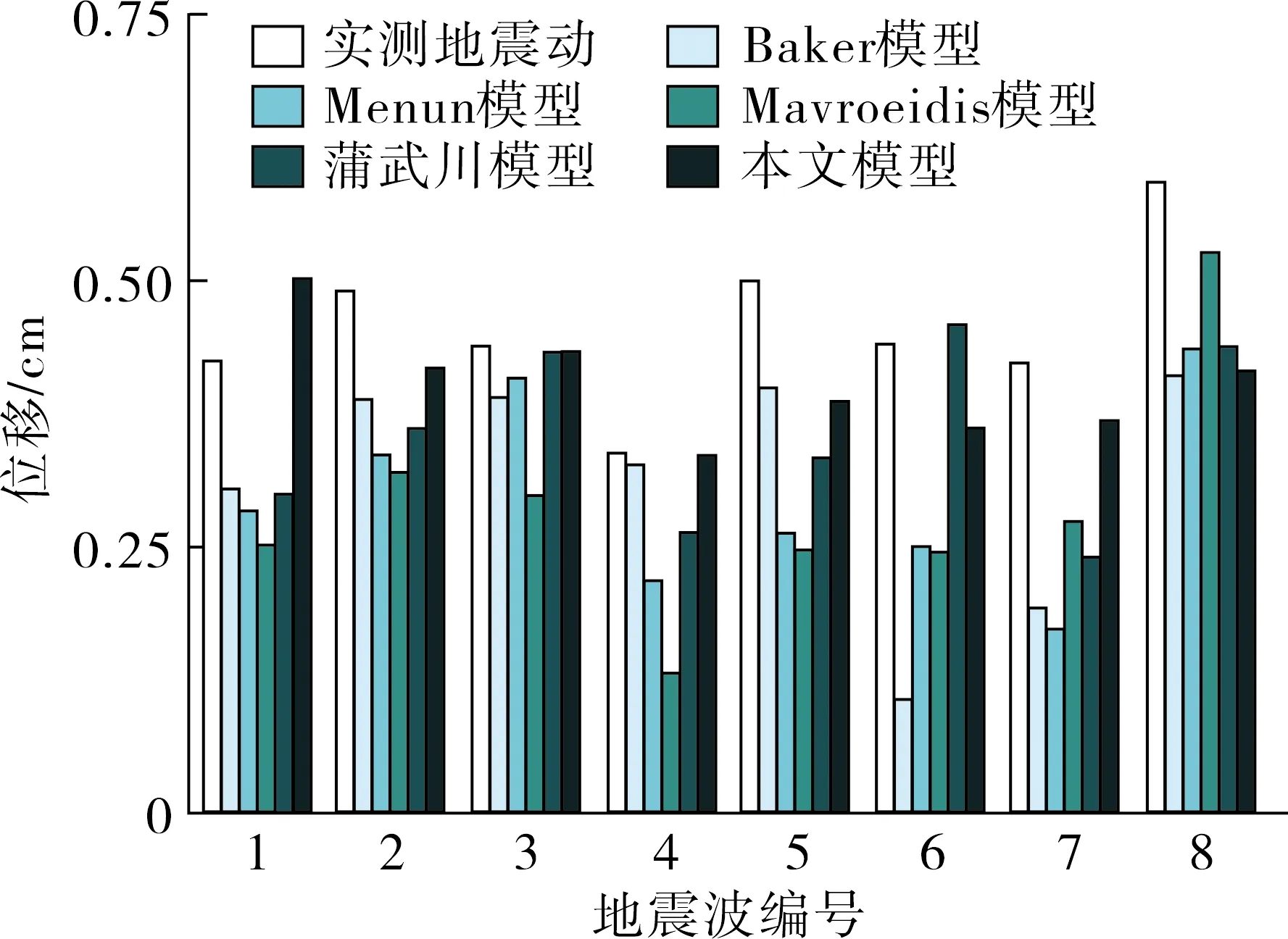
图7 2#墩墩顶最大位移值
由图5~7可知,同工况下的墩底弯矩、墩底剪力和墩顶位移结果趋势大致相同。本文以墩底弯矩结果为参考来分析地震响应结果。
首先分析单脉冲模型对各类型模拟地震动响应结果。1、2、3号单脉冲型模拟地震动的时程结果比较均衡,除Mavroeidis模型外实测地震动的响应结果误差在25%以内且小于实测地震动响应值,各模型间的误差也在30%以内。单脉冲模型模拟地震动的响应结果以Baker模型和蒲武川模型为最优,误差控制在20%以内。4、5、6号多脉冲型模拟地震动作用下随地震波和模拟方法变化地震动响应值变化很大。如Baker模型对4、6号波的误差值分别为11%、70%,出现明显的不稳定性,Baker模型和蒲武川模型对6号波的误差值分别为1%、70%,出现明显模型间的不稳定性。7、8号长周期型模拟地震动作用下的时程结果与4、5、6号波作用结果相似,即同一条波不同模拟方法、相同模拟方法对不同地震波的结果偏差均变化很大,其中蒲武川模型、Menun模型对地震波的模拟结果较好,其余2种模型对不同地震动的模拟出现很大差异。
从分析结果可知单脉冲模型对单脉冲型地震动的模拟比较优秀,对多脉冲型地震动和长周期地震动的模拟出现明显的不稳定性。以Baker模型和Menun模型最典型,对单脉冲型地震动的模拟较好,对其他2类地震动的模拟很差,蒲武川模型的模拟结果则相对较稳定。
相较于单脉冲模型,本文所提出的多脉冲模型的模拟结果有明显的提高。对单脉冲型地震动、多脉冲型地震动和长周期地震动的模拟结果误差最大分别为10%、22%、25%,虽对多脉冲型地震动和长周期型地震动模拟精度较单脉冲型地震动较弱,但模拟的精确度和稳定性较单脉冲模型均有明显提高。
5 结论
1) 本文基于小波变换的方法提出了多脉冲型地震动的模拟方法,通过与单脉冲模型的模拟结果对比,验证了本文方法对多脉冲型和长周期型地震动的模拟的可靠性,同时也不会影响对单脉冲地震动的模拟精度。
2) 本文基于加速时程为研究对象,相较于单脉冲模型基于速度时程为研究对象,从反应谱和时程响应结果可以看出,本文方法的模拟结果对短自振周期结构的响应更接近。
3) 从时程响应结果可知,时程响应结果对单脉冲型地震动、多脉冲型地震动和长周期地震动的模拟结果误差最大分别为10%、22%、25%,本文模型相较于单脉冲模型对不同类型地震动的模拟精度均有提升。
4) 本文模型较单脉冲模型考虑了一种模拟多脉冲型地震动的方法,但对于高频成分的模拟还需要更进一步的研究,有研究表明高频成分也具有一定能量且对短自振周期结构有较大损伤,需要进一步研究。
