Ultra-lightweight CNN design based on neural architecture search and knowledge distillation:A novel method to build the automatic recognition model of space target ISAR images

Hong Yng ,Y-sheng Zhng ,Cn-in Yin ,Wen-zhe Ding

a Space Engineering University,Beijing,101416,China

b Beijing Institute of Tracking and Telecommunications Technology,China

Keywords:Space target ISAR image Neural architecture search Knowledge distillation Lightweight model

ABSTRACT In this paper,a novel method of ultra-lightweight convolution neural network (CNN) design based on neural architecture search(NAS)and knowledge distillation(KD)is proposed.It can realize the automatic construction of the space target inverse synthetic aperture radar (ISAR) image recognition model with ultra-lightweight and high accuracy.This method introduces the NAS method into the radar image recognition for the first time,which solves the time-consuming and labor-consuming problems in the artificial design of the space target ISAR image automatic recognition model(STIIARM).On this basis,the NAS model's knowledge is transferred to the student model with lower computational complexity by the flow of the solution procedure(FSP)distillation method.Thus,the decline of recognition accuracy caused by the direct compression of model structural parameters can be effectively avoided,and the ultralightweight STIIARM can be obtained.In the method,the Inverted Linear Bottleneck (ILB) and Inverted Residual Block (IRB) are firstly taken as each block's basic structure in CNN.And the expansion ratio,output filter size,number of IRBs,and convolution kernel size are set as the search parameters to construct a hierarchical decomposition search space.Then,the recognition accuracy and computational complexity are taken as the objective function and constraint conditions,respectively,and the global optimization model of the CNN architecture search is established.Next,the simulated annealing (SA)algorithm is used as the search strategy to search out the lightweight and high accuracy STIIARM directly.After that,based on the three principles of similar block structure,the same corresponding channel number,and the minimum computational complexity,the more lightweight student model is designed,and the FSP matrix pairing between the NAS model and student model is completed.Finally,by minimizing the loss between the FSP matrix pairs of the NAS model and student model,the student model's weight adjustment is completed.Thus the ultra-lightweight and high accuracy STIIARM is obtained.The proposed method's effectiveness is verified by the simulation experiments on the ISAR image dataset of five types of space targets.

1.Introduction

Space target recognition based on two-dimensional ISAR images is the research focus in space situational awareness [1,2].The traditional target recognition methods based on radar images include two steps:(1) construct manually high discriminant features;(2)train specific classifiers to identify the target category,such as support vector machine (SVM),random forest (RF),and extreme gradient boosting (XGBoost) [3].Compared with the manual feature engineering,CNN realizes the end-to-end automatic target recognition,avoiding the tedious artificial feature construction and saving a lot of human resources and material resources.Therefore,many scholars have applied the CNN to the target recognition of radar images[4-6].For example,literature[4]studied an automatic synthetic aperture radar (SAR) target recognition method based on the visual cortex network;literature [5]proposed a fast semi-supervised ISAR image recognition method based on the full convolution region candidate networks and deep convolutional neural networks (DCNNs);literature [6] proposed a transferred DCNNs' stacking ensemble algorithm and realized the space target ISAR images'classification under the condition of small samples.The above researches have achieved high precision recognition of radar image targets.However,the models designed in these researches have high computational complexity and large storage space,so they are not suitable for portable mobile terminal deployment and other tasks that have a high limitation on storage devices and computing resources.Therefore,it is of great practical significance to further study building a lightweight space target ISAR image automatic recognition model(STIIARM)that meets the storage requirements and computational power limitations.

For the lightweight design of CNN,traditional methods mainly rely on the manual design of efficient network computing ways to reduce the model's parameters and calculation amount.For example,reduce the number of convolution kernels,reduce the number of feature map channels,and design efficient convolution operation mode.Many classic lightweight CNN models have been designed by the above methods,such as MobileNet [7,8],ThunderNet[9],ShuffleNet[10,11],SqueezeNet[12],etc.Although these artificial models have made remarkable achievements,their design requires a great deal of time and human resources due to the need to consider various factors such as the connection mode between layers,network depth,and convolution calculation method.Therefore,to improve the model design efficiency,we adopt the neural architecture search (NAS) method to design the STIIARM with lightweight and high recognition accuracy.

NAS refers to the method that can automatically search out the high-performance CNN model in a specific search space through a particular search strategy.At present,the CNN model's performance designed by the NAS method has shown good performance on visual tasks such as image classification [13] and semantic segmentation [14].The NAS's search space can be divided into the global search space for directly searching the entire CNN architecture and the local search space for forming the whole CNN architecture by searching and repeating some specific structures.The global search space mainly includes the chained architecture search space [15] and the multi-branch architecture search space [16],while the local search space mainly consists of the block architecture search space [17].For the global search space,the search process requires a lot of time and computing resources because of its wide search range and massive parameter scale.Besides,due to the lack of constraints on the CNN structure in the global search space,the search process is often difficult to converge or converge to the local suboptimal CNN structure.Compared with the global search space,the block architecture search space reduces the search scope to the repetition number of the blocks and the specific block parameters such as convolution type,convolution kernel size,and output filter size.It significantly reduces the search space scale and therefore is more suitable for the search of STIIARM.However,the traditional block architecture search space only searches the structure parameters in a block,so the constructed CNN model will lose the diversity among layers,resulting in the limitation of the searched model's classification performance.Therefore,we adopt a local search space construction method based on hierarchical decomposition [18-20].This method first decomposes CNN into different blocks and then sets the search space for each block,effectively ensuring the built model's layer diversity.

The NAS's search strategy determines how to search out the required optimal CNN model in the search space.Currently,the commonly used search strategies are supernet-based search strategies [21,22],those based on the reinforcement learning (RL)method [17],and those based on the heuristic algorithm [13].Among them,the supernet-based search strategy has the highest search efficiency.It builds a super-large network based on the search space and then trains the supernet once to obtain all subnetworks weights.However,due to the supernet model's complex structure and the limited number of space target ISAR images that can be obtained,it is easy to cause overfitting in the supernet's training.Simultaneously,since the sub-networks in the supernet are not separately trained,the search model's final effect cannot be guaranteed.The search strategy based on the RL method is computationally expensive and time-consuming,and the search efficiency is low.In contrast,the search strategy based on the heuristic algorithm has faster search speed and strong robustness,which can significantly improve search efficiency,so it is more suitable for the search of STIIARM.However,for search strategies based on swarm intelligence algorithms such as genetic algorithm(GA) [23],particle swarm algorithm (PSA) [24],and ant colony algorithm (AC) [25],one iteration of the algorithm requires simultaneous training and evaluate multiple models.This requires high computing performance for computing platforms,and ordinary computing platforms cannot run at all.In this regard,to enable the NAS method to be implemented on common computing platforms,we adopted a search strategy based on the simulated annealing(SA) algorithm.Unlike the swarm intelligence-based heuristic algorithms,the search strategy based on the SA algorithm only trains a single neural network model for each iteration so that the common computing platform can meet the algorithm's operation memory requirements.However,the SA algorithm is unsuitable for solving multi-objective optimization problems,so we adopt a twostage strategy to obtain the ultra-lightweight STIIARM.In the first stage,we use the recognition accuracy rate as a single objective function.By combining the above search space design method and the simulated annealing algorithm,we search for a STIIARM with high recognition accuracy.In the second stage,we use model compression technology to simplify the network structure further,to obtain an ultra-lightweight STIIARM while maintaining a high model recognition accuracy.

At present,Common model compression methods include network pruning,weight quantization,low-rank decomposition,and knowledge distillation (KD) [26-29].Among them,network pruning reduces CNN's redundant parameters by pruning the weights in the CNN structure;weight quantization reduces the model size by reducing the model weight expression precision;low-rank decomposition achieves model compression by using a low-rank matrix to approximate the original weight matrix.The above three model compression methods are implemented by directly processing the original model.For the STIIARM searched by the NAS method,its structural parameter redundancy is relatively low.If the STIIARM is compressed directly by the above three methods,the STIIARM's recognition accuracy will be greatly reduced.Therefore,we use the KD method to compress the STIIARM.Unlike the model compression method that directly deals with the original model's structural parameters,the KD method creates a smaller student model to fit the original model's weight distribution (teacher model),thus transferring the larger model's knowledge to the smaller model.However,the traditional KD method only allows the student model to fit the teacher model's output soft label,which limits the knowledge extraction scope of the student model from the teacher model.In this regard,we use the flow of the solution procedure(FSP)distillation method[30]to compress the STIIARM further.The FSP distillation method makes the student model fit the FSP matrix of the teacher model.That is to allow the student model to learn the teacher model's feature representation method,thereby improving the final distillation effect of the model.

In summary,in order to achieve a lightweight design for the ISAR image recognition model for space targets,we propose a twostage design scheme based on automatic architecture search and knowledge distillation.The first stage uses the NAS method to search for a space target ISAR image recognition model with high recognition accuracy;the second stage uses the FSP distillation method to compress the searched model to be lighter.In the first stage,to enable the NAS method to be efficiently implemented on a common computing platform,we constructed a block-based decomposition hierarchical search space,and the SA algorithm is adopted as the NAS search strategy.In the second stage,to avoid the reduction of recognition accuracy caused by the search model's direct compression,we adopted the FSP distillation method to reduce the model's computational complexity and volume indirectly.To effectively link the NAS method and the FSP distillation method,we also proposed a corresponding student model design strategy.In general,we propose a feasible solution to the design problem of the ultra-lightweight STIIARM.This scheme can be implemented on a common computing platform and provide ideas for the lightweight design of other recognition models in engineering.The main contributions of this article are as follows:

(1) For the first time,the NAS method is introduced into the radar image recognition task.By designing the block-based hierarchical decomposition search space,the CNN layer diversity is guaranteed,and the overall scale of the search space is effectively reduced.Using SA as a search strategy ensures that only a single network model is trained and evaluated in each iteration during the search process,which effectively reduces model search difficulty.Compared with the traditional manual-based CNN design method,the NAS method can automatically search out the STIIARM with high recognition accuracy and low computational complexity without consuming much time and human resources.

(2) Combine the FSP distillation method and the NAS method to design an ultra-lightweight recognition model for ISAR images of space targets.A student model design method is proposed based on the principles of a similar block structure,the same number of corresponding channels,and the lowest model computational complexity.On this basis,a student model with lower computational complexity than the NAS model is designed.A“one-to-one”distillation strategy is proposed.The student model's weight is adjusted by minimizing FSP matrix pairs' loss between the NAS and student models.The knowledge transfer from the NAS model to the student model is then completed.On the premise of retaining the NAS model's high accuracy,a STIIARM with lower computational complexity is further obtained.

2.STIIARM search based on the SANAS method

If the traditional manual design method is used to design the lightweight STIIARM,we not only need to consider the network depth,network convolution calculation method,and network layer connection method but also need to continuously adjust the network structure according to the model's training performance.That will consume a lot of human resources and material resources.Therefore,to reduce designers' burden and improve design efficiency,in this section,we adopt the neural network architecture search based on the simulated annealing algorithm (SANAS) to design the STIIARM automatically.Firstly,to speed up the search efficiency,we design the STIIARM's search space based on hierarchical decomposition.Secondly,to take into account both model recognition accuracy and model search efficiency,we use model recognition accuracy and floating-point operations as performance evaluation indicators in the model search process.Finally,to quickly search out the global optimal network model on a common computing platform,we formulated the model search strategy based on SA.Through the above method,it is possible to directly search for STIIARM with good performance,thereby avoiding the dependence on the designer's experience and solving the timeconsuming and labor-consuming problems of manually designing the network.

2.1.Construction of the block-based hierarchical decomposition search space

The search space defines the basic architecture unit for constructing the network model.An adequate search space determines the network model's search efficiency and performance.To narrow the model search range and ensure the diversity of the model layers,in this section,we propose a local search space construction method based on the hierarchical decomposition method and use this method to construct the STIIARM's search space.

Unlike the traditional block architecture search space,the hierarchical decomposition search space first decomposes the CNN model into different blocks.Then search for the internal structure of each block.Each block consists of a series of units.The search variables are specified as the internal parameters and repetitions of each unit.To ensure that the searched CNN is lightweight,we use Inverted Linear Bottleneck (ILB) and Inverted Residual Block (IRB)as the block's base unit structure.The structures of these two units are shown in Fig.1.

IRB uses depthwise (DW) convolution [7] instead of standard convolution,which significantly reduces the computational complexity.Simultaneously,it adds a layer of 1×1 Pointwise(PW)convolution [7] before DW convolution to increase the number of channels,thus improving the model effect.After DW convolution,1 × 1 PW convolution is used to reduce the number of channels,and the input and output are connected.Among them,the first PW convolution layer and the middle DW convolution layer both adopt a nonlinear activation layer-rectified linear unit(ReLU)to improve the nonlinear expression ability of features.The last PW convolution layer uses the linear activation function instead of the traditional ReLU,which effectively solves information loss of low dimensional features.The ILB's structure is similar to that of the IRB,except that the shortcut connection between the IRB's input and output layers is removed.

To determine the internal parameters of the unit structure and the number of units in each block,we set the search variables to four types:the size of the expansion ratio (SE ratio),output filter size (the number of channels),the number of IRBs,and the convolution kernel size.We use a string of tokens to represent each block's search space,and each token represents the index position of the corresponding search variable.Fig.2 shows the structure of the hierarchical decomposition search space.

Suppose that the search range corresponding to the search variables are:(1)SE ratio:1,2,3,4;(2)output filter size:3,4,8,12,16,24,32,48,64,80,96,128,144,160,192;(3)number of IRBs:0,1,2,3;(4)convolution kernel size:3×3,5×5.Then we can express the search space of each block as (0,0,0,0)～(3,14,3,1).For example,tokens(2,14,2,0,3,4,3,1)indicates that the CNN model consists of two blocks.Tokens (2,14,2,0) corresponds to the first block structure,in which the SE ratio is 3,the output filter size is 192,the number of IRBs is 2,and the convolution kernel size is 3;tokens(3,4,3,1)corresponds to the second block,in which the SE ratio is 4,the output filter size is 16,the number of IRBs is 3,and the convolution kernel size is 5×5.The corresponding CNN structure is shown in Fig.3.

Fig.1.Inverted linear bottleneck and inverted residual block.

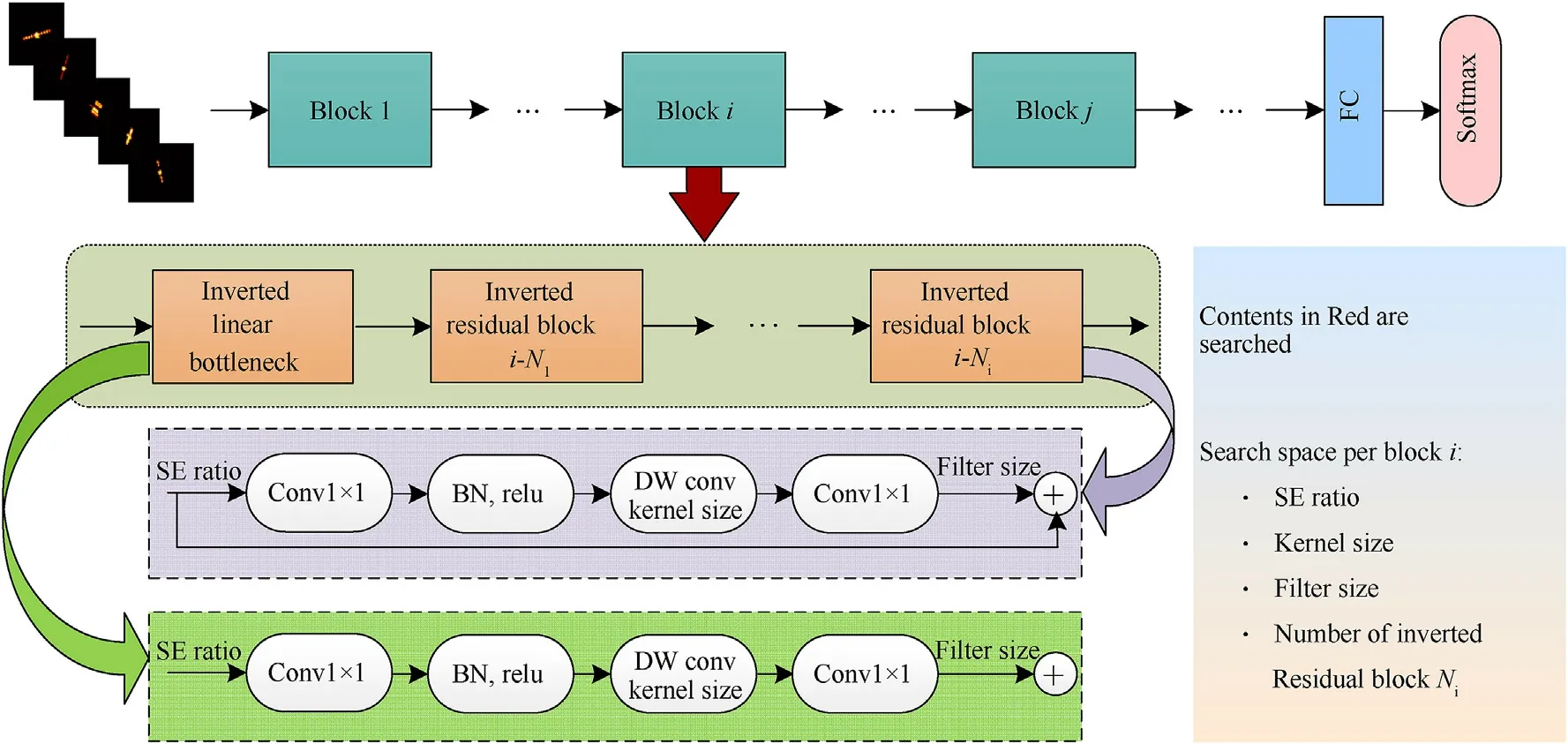
Fig.2.Schematic diagram of hierarchical decomposition search space.

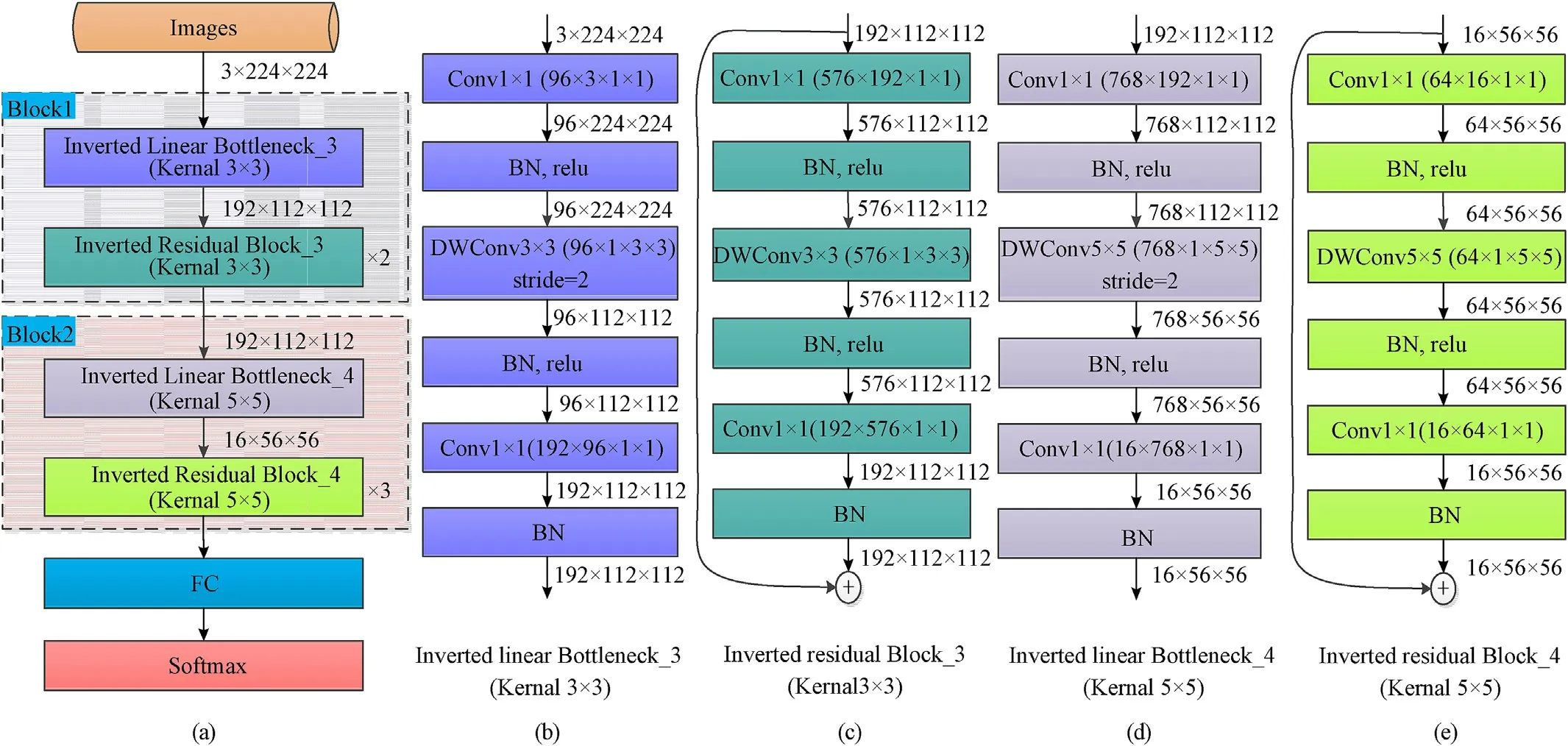
Fig.3.Schematic diagram of the CNN structure corresponding to tokens (2,14,2,0,3,4,3,1).

2.2.Design of the evaluation index and formulation of the search strategy

We have completed the construction of the model search space in Section 2.1.Next,we need to develop the corresponding model search strategy further.The purpose of formulating the search strategy is to search for the optimal global model under the premise of ensuring search efficiency.To this end,we first need to establish relevant performance evaluation indexes.We take the model's recognition accuracy of the space target ISAR image as a performance evaluation index to ensure that the searched model has high recognition accuracy.Simultaneously,to enhance the search efficiency and enable the searched model to have strong real-time computing ability,we take the model's computational complexity as another performance evaluation index.The recognition accuracy(ACC) is the ratio that the correctly predicted ISAR image samples are to the total ISAR image samples.The computational complexity is measured by the floating points of operations (FLOPs).

The specific calculation method of FLOPs is as follows [31]:

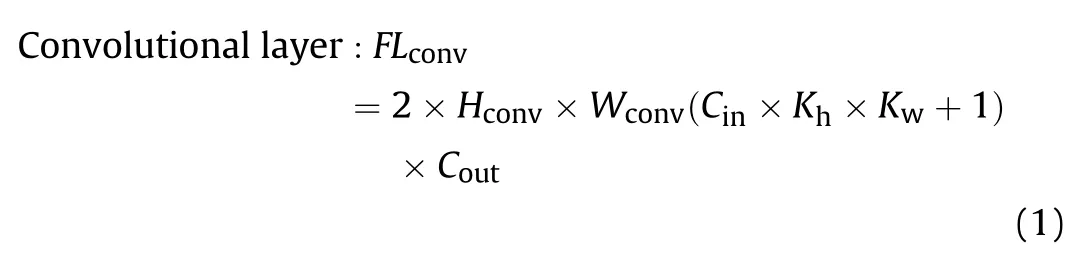
where FLis the FLOPs of the convolution layer;Hand Ware the height and width of the input feature map,respectively;Cand Care the number of channels of the input feature map and the output feature map,respectively;Kis the kernal height,and Kis the kernal width.

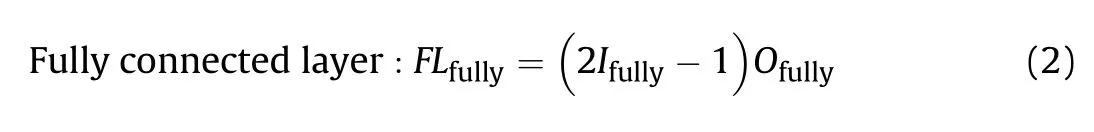
where FLis the FLOPs of the fully connected layer;Iis the number of input neurons;Ois the number of output neurons.

On this basis,we take the model's recognition accuracy and the model's computational complexity as the objective function and constraint conditions,respectively.The optimization model is established as follows:

where Mod represents the searched CNN model;ACC(Mod) represents the recognition accuracy of CNN model to ISAR image of space target;FL (Mod) represents the FLOPs of CNN model;FLrepresents the maximum allowable FLOPs.

To quickly and accurately search out the global optimal STIIARM,we also need to formulate a good search strategy for solving Eq.(3).The RL method was often used as NAS's search strategy in the early days [32].However,the RL method has high computational complexity and time-consuming,resulting in low efficiency of the whole search process.In addition,the heuristic search strategy based on population evolution needs to operate on the population,and dozens of neural network models need to be trained and evaluated simultaneously during the entire search process,making it difficult for the algorithm to run on common computing platforms.Compared with the population evolution algorithm,the SA algorithm only operates on a single individual.It only needs to train a single neural network model for each iteration in the entire search process.Therefore,the common computing platform can meet the algorithm running memory requirements.In this regard,we choose the SA algorithm as the search strategy of the network model.

The SA algorithm simulates the process of metal cooling to the lowest energy state after a hot bath.It obtains the optimal global solution of the optimization problem by likening the optimization problem's objective function to the metal system's energy.Recently,this algorithm has been widely used in various disciplines to solve nonlinear system optimization problems [33-35].The essential structure of the SA algorithm can be divided into internal and external circulations.For the external circulation,to avoid the SA algorithm falling into the local optimum,we set the update function of temperature as T＝γTto keep the temperature decreasing gradually.Where Tand Texpress the temperatures at the(k+1)-th and k-th annealing operations,respectively;γ is the temperature attenuation coefficient,and γ∈]0，1［.For internal circulation,to fully simulate the thermal motion of molecules and explore the search space with search potential,we use the Metropolis criterion to judge whether to accept the newly generated CNN model.In the k-th annealing process,the probability of accepting the new CNN model is assumed to be

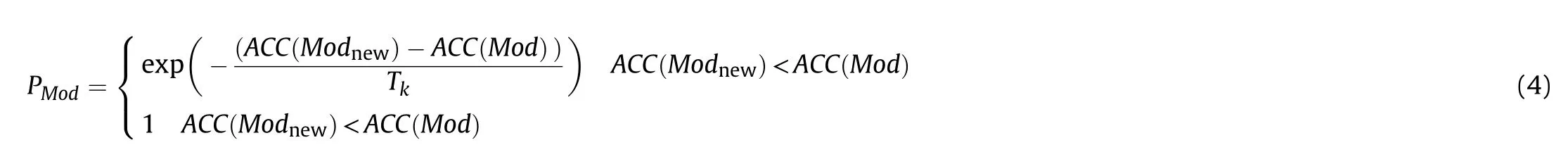
where ACC (Mod) represents the recognition accuracy of the new CNN model for space target ISAR image.At the beginning of the search,the recognition accuracy of the CNN model is initialized to 0.

According to the description in Section 2.1,the CNN model is represented by a string of tokens.Therefore,in the entire optimization process,we randomly modify a part of tokens each time to generate a new string of tokens and then map the new tokens back to the model structure to continue optimization.To shorten the overall search time,before calculating the objective function ACC(Mod),we only train a particular epoch for the newly generated model.Until the end of the search,we will conduct complete training on the searched optimal CNN model.Algorithm 1 gives the specific steps of using SANAS to search the STIIARM.

3.Construction of ultra-lightweight STIIARM based on the FSP distillation method

Since the computational complexity of the optimal STIIARM Modis relatively low,in order to further reduce its redundant parameters,we use the KD method to compress the Mod.In the traditional KD method research,the student model is generally used to fit the soft label produced by the teacher model [36],thus inducing the student model to train.However,in this way,the student model can only learn the teacher model's softmax layer knowledge,which limits the final distillation effect.In this regard,we take the optimal STIIARM Modas the teacher model and generate the corresponding FSP matrix in the block of the model Mod.By making the student model fit the FSP matrix of the teacher model,the student model can learn the process and method of the teacher model in solving problems,thereby enhancing the distillation effect.

3.1.Design method of the ultra-lightweight student model

KD method is an efficient model compression method based on the“teacher-student”framework.Its core idea is to use the compact student model to simulate the complex teacher model,thus completing the knowledge transfer from the teacher model to the student model.Since the KD method is easy to understand and implement,it has been widely used in academic and industrial circles and has achieved good results [37-39].Before distillation,we need to design the structure of the student model.Compared with the Modopt,which is a teacher model,the student model structure needs to be more simplified.However,there is no fixed design method for the student model structure,which is usually designed by human experience.Therefore,to enable the student model to maximize the learning of the teacher model's existing knowledge while maintaining a low computational complexity,we design the student model based on the three principles of similar block structure,the same corresponding channel number,and the minimum computational complexity.

(1) The principle of the similar block structure

When the teacher model uses the space target ISAR images for learning and training,the resolution of the output feature map corresponding to each block decreases with the deepening of the network.For example,for the teacher model shown in Fig.3,its output feature map's resolution decreases from 112 × 112 of the first block to 56×56 of the second block.If the number of blocks in the student model is 1,the student model's output feature map resolution is 112 × 112,which lacks the learning process for the feature map with a resolution of 56×56.It can be seen that if the number of blocks in the student model is less than 2,the student model will not maintain a feature learning process similar to that of the teacher model,resulting in the student model's limited learning ability.On the contrary,if the number of blocks in the student model is greater than 2,the student model's computational complexity may exceed the teacher model,so it is not easy to ensure the lightweight of the student model.In summary,when designing the student model,we keep the number of blocks in the student model consistent with the teacher model.

(2) The principle of the same corresponding channel number

The principle of block structure similarity ensures that the number of blocks in the student model is consistent with the teacher model.To make the guidance of the teacher model more pertinent,we adopt a one-to-one distillation strategy during distillation.The so-called one-to-one distillation strategy means that the ℓ-th block in the teacher model only guides the ℓ-th block corresponding to the student model,which ensures that the teacher model can more accurately impart its characteristic representation rules to the student model.Therefore,during distillation,it is necessary to ensure that the FSP matrix's size generated by the corresponding block of the teacher model and the student model is equal.At this time,the channel number of the block for distillation learning in the student model needs to be equal to the channel number of the block corresponding to the teacher model.For example,if the second block in the teacher model shown in Fig.3 is used to guide the student model,the number of channels in the second block should be 16 when designing the student model.

(3) The principle of the minimum computational complexity

When designing the student model,keep the computational complexity of each block to a minimum.It can be seen from Eqs.(1)and (2) that under the condition that the resolution of input and output feature maps are determined,the model's FLOPs are mainly determined by the channel number,the convolution kernel size,and the convolution kernel number in each block.The fewer the channel number,the smaller the convolution kernel size,and the fewer the convolution kernel number,the lower the model block's computational complexity.Therefore,to design an ultralightweight student model,under the premise of ensuring the same corresponding channel number,we set the SE ratio,the output channel number,and the convolution kernel size of each block in the student model to the minimum value in their search range.Thereby,ensure each block's channel number to be least and each block's convolution kernel size to be smallest.Besides,to ensure the convolution kernel number in each block to be the least,we make every block in the student model contain only the minimum number of IRBs.

After completing the block structure design based on the above three design principles,we continue to add a fully connected layer,a softmax layer,and a classification layer at the end of the student model to ensure the student model's integrity.For example,taking the model shown in Fig.3 as the teacher model,according to the above design principles,three student model structures can be obtained.Their tokens are(0,14,0,0,0,0,0,0),(0,0,0,0,0,4,0,0),and(0,14,0,0,0,4,0,0),respectively.Different tokens correspond to different model distillation strategies.Tokens(0,14,0,0,0,0,0,0,0)means using the first block of the teacher model to guide the first block of the student model;tokens(0,0,0,0,0,4,0,0)means using the second block of the teacher model to guide the second block of the student model;tokens(0,14,0,0,0,4,0,0) means using both two blocks of the teacher model to guide the two blocks of the student model simultaneously.Since the above three student models have similar model structures(only the number of channels is different),we only take tokens(0,0,0,0,0,4,0,0)as an example to show its corresponding model structures in Fig.4.

3.2.STIIARM compression based on the FSP distillation method

Next,we use the FSP distillation method to transfer the knowledge of the searched optimal STIIARM Modto the student model with a smaller network structure,further reducing the model size on the premise of ensuring model recognition accuracy.Fig.5 shows the entire FSP distillation framework.

In Fig.5,the FSP matrix is calculated by the feature maps extracted from the two layers of the network.And the specific calculation expression is shown in Eq.(5) [40]:

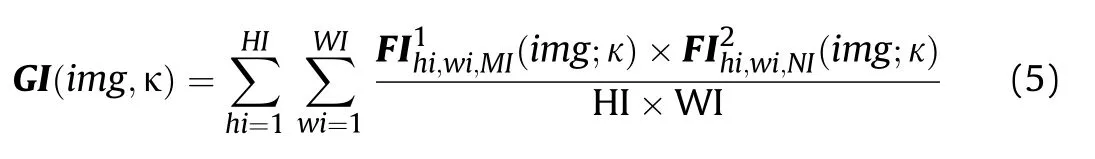
where GI is the FSP matrix;img represents the input space target ISAR images;κ represents the weights of the model Mod;FIis the feature map extracted from network layer 1;FIis the feature map extracted from network layer 2;MI and NI are the channel number of the feature maps of network layer 1 and network layer 2,respectively;HI and WI are the height and width of the feature maps of network layer 1 and network layer 2,respectively.

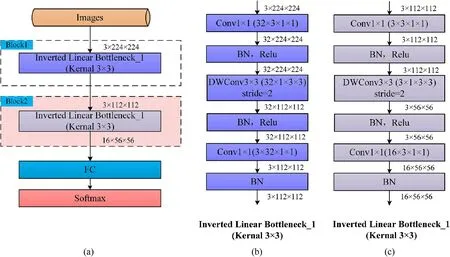
Fig.4.The student model structure corresponding to tokens (0,0,0,0,0,4,0,0).

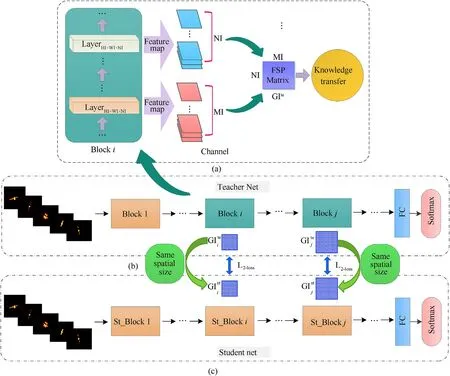
Fig.5.FSP distillation framework.

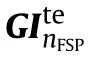
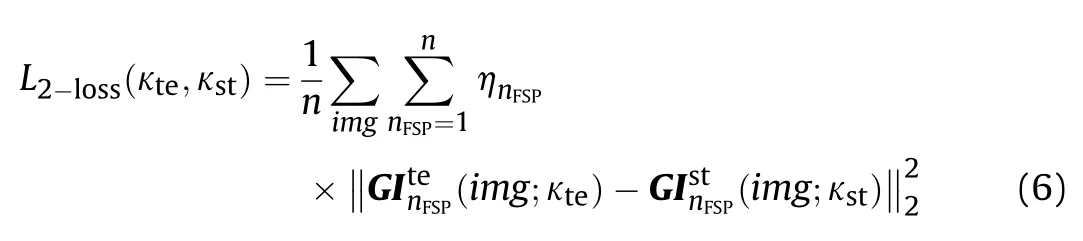
During the training process,the student model's weights can be determined by minimizing the Lof the FSP matrix pairs between the teacher and student models.Algorithm 2 gives the specific steps of compressing the optimal STIIARM Modby the FSP distillation method.After the model compression is completed,we can deploy the ultra-lightweight STIIARM to the mobile terminal with the help of Baidu PaddlePaddle's lightweight inference engine Paddle Lite.First,configure the Java environment for model deployment on the mobile terminal through Android Studio and the Java Development Kit (JDK).Then,use Paddle Lite's opt tool to convert the model into a naive buffer format file.And based on the Java application program interface (API),an ultra-lightweight STIIARM software for mobile deployment is developed.Finally,through virtual terminal debugging,the successfully debugged model is deployed to the entity mobile terminal for application.In summary,the complete building process of lightweight STIIARM is given in Fig.6.

Fig.6.Design flow diagram of ultra-lightweight STIIARM.

Fig.7.Three-dimensional grid models of five types of space targets and their corresponding ISAR image examples.

Fig.8.Partial ISAR image samples of five types of space targets.

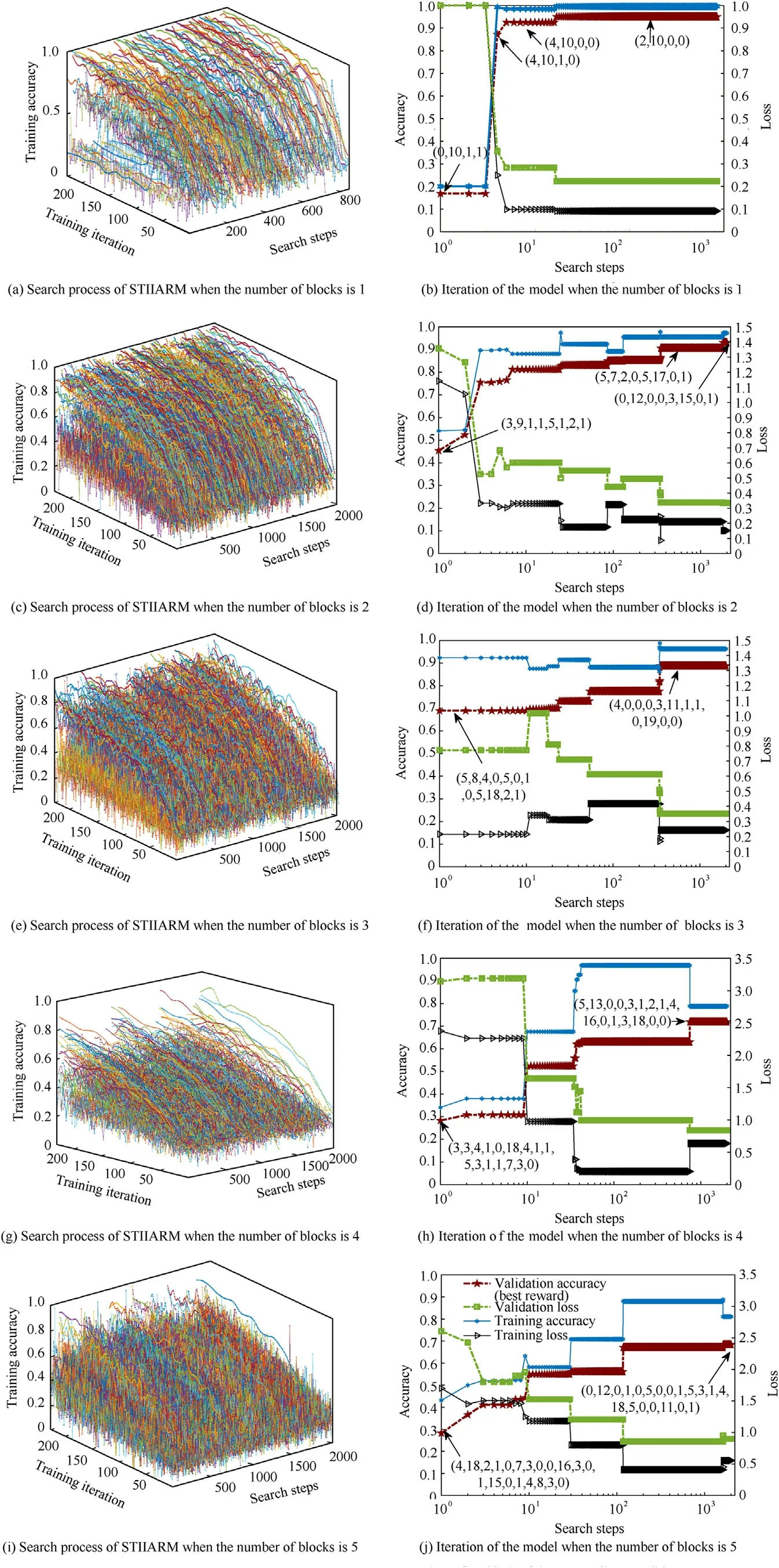
Fig.9.Searching process of optimal STIIARM structure under five kinds of downsampling conditions.

4.Experiment validation

4.1.Dataset,experimental environment and performance metrics

4.1.1.Dataset generation of the space target ISAR image

When constructing the ISAR image data set of the space target,the 3DMAX software is first used to establish the threedimensional mesh model of the five types of space targets.The specific model structure of the established space target is shown in Fig.7.A simulation environment for ISAR imaging is set up with reference to the regular on-orbit status of the targets.In the satellite tool kit (STK) environment,Satellite1～Satellite5 is placed on a circular orbit with an orbit altitude of 788.9 km,an orbit inclination of 98.57,and a right ascension of ascending node of 99.44.Meanwhile,the radar is placed at 29.5N and 119E.The LMF with pulse frequency f＝10 GHz,bandwidth B＝1 GHZ,and pulse width T＝1 × 10s is used to illuminate the Satellite1～Satellite5.The radar echo data is collected,and the sampling frequency is f＝1×10HZ.The received radar echoes are processed,and the initial ISAR images of five types of space targets can be obtained.The speckle reduction operation is used to process all ISAR images,and 292 ISAR images corresponding to each type of satellite are selected to form a space target ISAR image dataset.Fig.8 shows a part of the ISAR image data after speckle reduction.

4.1.2.Experimental environment and model performance metrics

In the following simulation experiments,we adopt a unified environment configuration.GPU is Tesla V100;VIDEO MEM is 32 GB;CPU is Intel 4 cores;RAM is 32 GB;DISK is 100G;programming environment is python 3.7.

In addition to the recognition accuracy ACC and the floating points of operations FLOPs,the cross-entropy loss C,precision PPV,sensitivity TPR,and comprehensive evaluation index F1-Score F1 are also selected as the additional performance metrics to measure the performance of the model.The specific calculation method is as follows:

Fig.10.The optimal model structure obtained when the number of blocks is 4.

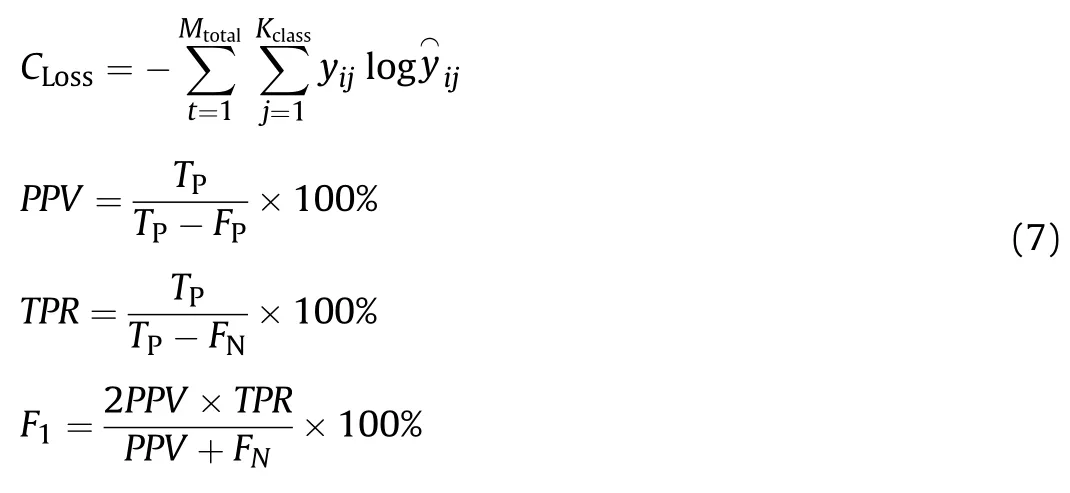
4.2.Search experiment of STIIARM based on the SANAS

4.2.1.Search for the high-performance STIIARM

Before searching,we first determine the search range corresponding to the search variables in the hierarchical decomposition search space.To ensure the diversity of the STIIARM's internal structure and the model search efficiency,we set the search ranges corresponding to the four search variables in the model block as:(1)SE ratio:1,2,3,4,5,6;(2)output filter size:3,4,8,12,16,24,32,48,64,80,96,128,144,160,192,224,256,320,384,512;(3)number of IRBs:0,1,2,3,4,5;(4)convolution kernel size:3×3,5×5.Then,the search space of each block can be expressed as(0,0,0,0)～(5,19,5,1).Within the model search process,the model's downsampling number is set equal to the number of its blocks.For example,when the model's downsampling number is 2,we also set the model's block number to 2.

Taking into account that the initial STIIARM Modis randomly generated in the search space,to ensure that the search process is sufficient,we set the initial temperature Tof the SA algorithm to 1000,the temperature attenuation coefficient to 0.95,and the number of temperature attenuations to 100.The number of inner cycles L under each annealing temperature Tis set to 20,and the maximum number of attempts to generate a new model Numis set to 50,000.The smaller the maximum FLOPs FLis,the lower the model's computational complexity is.However,if FLis too small,it will affect the generation of the model and the final model performance.Therefore,referring to the model computational complexity of MobileNetV2 (FLOPs＝3,1234,5728),we set the maximum FLOPs FLto about ten times that of MobileNetV2,that is,FL＝32,1208,5440.According to Algorithm 1,every time a new model is searched,it needs to be trained and evaluated.To prevent the model training time from being too long and affecting the overall search speed,we set the model training epoch Nto be 6 in each search step.Besides,set the model's learning rate to 1 × 10and the batch size to 32,1190 and 135 ISAR images are taken in the training set and validation set,respectively.

In the next simulation experiment,we set the number of blocks in the model to 1 to 5 according to different downsampling times(that is,the output feature map size of the model is 112,56,28,14,and 7,respectively).Based on the above simulation condition settings,the optimal model structure corresponding to the five downsampling conditions can be searched according to Algorithm 1.The specific search process is shown in Fig.9.

Fig.9 (a),(c),(e),(g),(i) is the search process of the STIIARM structure when the number of blocks is 1,2,3,4,and 5,respectively.The x-axis represents the search steps of the SANAS algorithm;the y-axis represents each generated model's training iterations.The zaxis represents the generated model's training accuracy.It can be seen that using the SA algorithm as the search strategy of the STIIARM structure,only a single model is trained and evaluated in each search step,which effectively reduces the search difficulty.Considering that the structure of the optimization model is updated rapidly in the early stage of the iterative search process,we use the logarithmic coordinate system to describe the change of the optimal reward model with iteration,as shown in Fig.9(b),(d),(f),(h) and (j).The x-axis represents the search steps of the SANAS algorithm.The left y-axis represents the ‘training accuracy and verification accuracy corresponding to the optimal reward model;the right y-axis represents the training loss and verification loss corresponding to the optimal reward model.For better display,Fig.9(b),(d),(f),(h),and(j)only show a part of the current optimal tokens.

Fig.11.DA examples of 5 types of space target ISAR images.A represents the original ISAR image;b represents the ISAR image after standardization;c,d,and e are ISAR images after contrast enhancement;f and g are ISAR images after small angle rotation;h and i are ISAR images after the azimuth-scale change;j and k are ISAR images after the distance-scale change.

Table 1 The scale of the training set,validation set,and test set after DA operation.

Fig.9 shows that when the block number is 1,the search algorithm stops after 845 iterations.At this point,the number of attempts to generate the current new model has reached the maximum attempts Numwe set.The searched optimal model tokens is (2,10,0,0).The training accuracy,training loss,verification accuracy(optimal reward),and verification loss corresponding to the optimal model are 0.9961,0.0916,0.9500,and 0.2239,respectively.When the number of model blocks is 2,the search algorithm terminates after 2000 iterations.The optimal model tokens is (0,12,0,0,3,15,0,1).The training accuracy,training loss,verification accuracy,and verification loss of the optimal model are 0.9729,0.1521,0.9313,and 0.3350.When the number of model blocks is 3,the algorithm terminates after 2000 iterations.The optimal model tokens is(4,0,0,0,3,11,1,1,0,19,0,0).The training accuracy,training loss,verification accuracy,and verification loss of the optimal model are 0.9625,0.2428,0.8875,and 0.3507.When the number of model blocks is 4,the search algorithm stops after 2000 iterations.The optimal model token is(5,13,0,0,3,1,2,1,4,16,0,1,3,18,0,0).The training accuracy,training loss,verification accuracy,and verification loss of the optimal model are 0.7884,0.6362,0.7188,and 0.8415.Finally,when the number of model blocks is 5,the search algorithm terminates after 2000 iterations.The optimal model token is(0,12,0,1,0,5,0,0,1,5,3,1,4,18,5,0,0,11,0,1).The training accuracy,training loss,verification accuracy,and verification loss of the optimal model are 0.8108,0.5541,0.6839,and 0.8973.

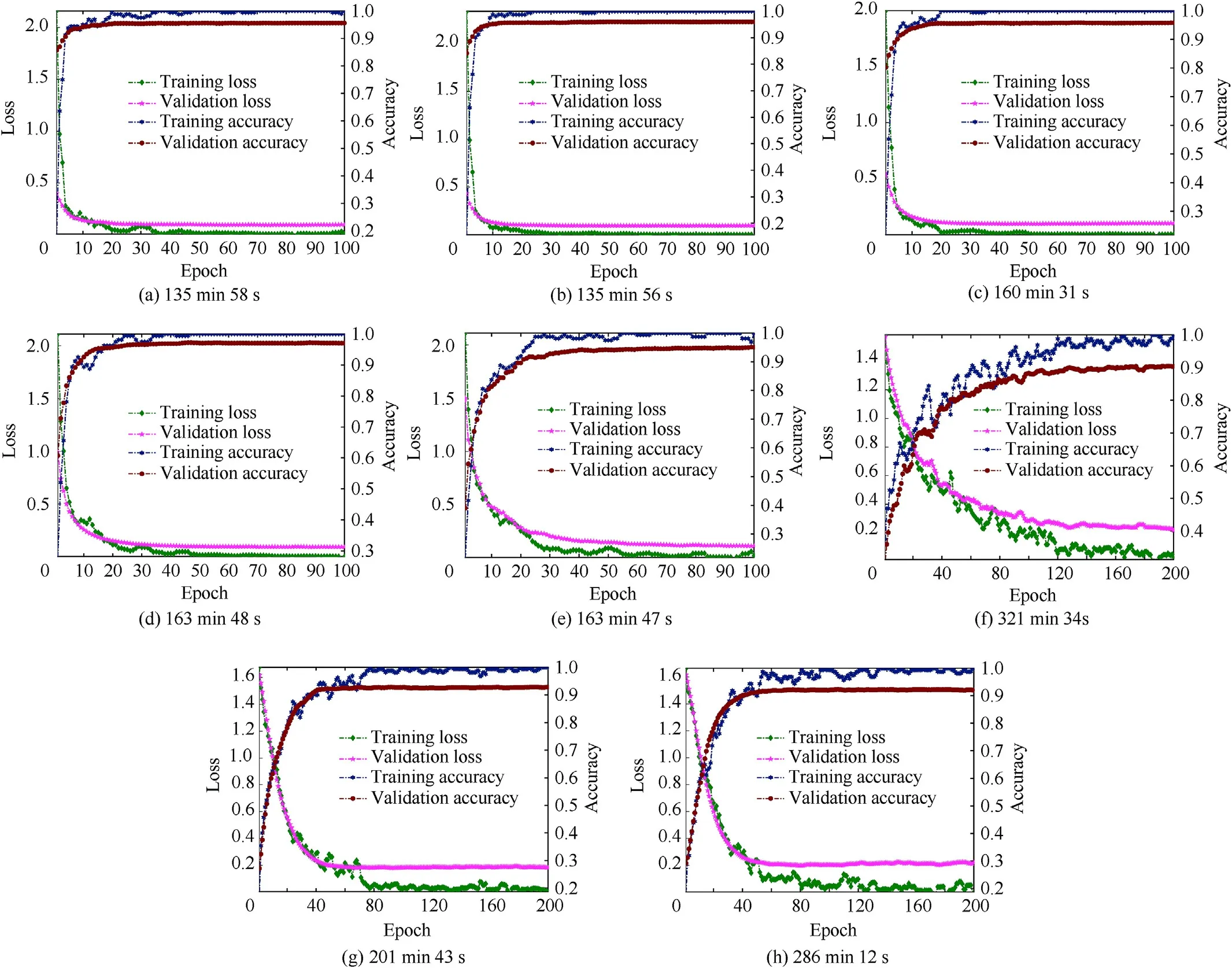
Fig.12.Comparison of the training process between the optimal models and the MobilenetV2 and MobilenetV3 models.(a)Retraining process of 1BlockNet model;(b)retraining process of 2BlockNet model;(c)retraining process of 3BlockNet model;(d)retraining process of 4BlockNet model;(e)retraining process of 5BlockNet model;(f)training process of MobilenetV2 model;(g) training process of MobilenetV3-Small model;(h) training process of MobilenetV3-Large model.

Fig.13.Test results of the eight models.(a)Test confusion matrix of 1BlockNet model;(b)test confusion matrix of 2BlockNet model;(c)test confusion matrix of 3BlockNet model;(d) test confusion matrix of 4BlockNet model;(e) test confusion matrix of 5BlockNet model;(f) test confusion matrix of MobilenetV2 model;(g) test confusion matrix of MobilenetV3-Small model;(h) test confusion matrix of MobilenetV3-Large model.

It can be seen from the above results that when the search algorithm terminates,the optimal models' structure has remained stable,and each model has rich layer diversity,which verifies the effectiveness of the hierarchical decomposition search space design method proposed in this paper.To save space,we only give the corresponding network structure when the number of blocks is 4,as shown in Fig.10.For the convenience of description,next we name the models corresponding to tokens(2,10,0,0),tokens(0,12,0,0,3,15,0,1),tokens(4,0,0,0,3,11,1,1,0,19,0,0),tokens(5,13,0,0,3,1,2,1,4,16,0,1,3,18,0,0),and tokens(0,12,0,1,0,5,0,0,1,5,3,1,4,18,5,0,0,11,0,1) as 1BlockNet,2BlockNet,3BlockNet,4BlockNet,and 5BlockNet,respectively.FLOPs of models 1BlockNet～5BlockNet are 1,4089,4688.0,15,5646,0640.0,6,0922,7008.0,20,7100,6912.0,and 18,6665,2896.0,respectively.

4.2.2.Retraining of the optimal model

Since the number of training epochs during the model search is set to be small,it cannot fully demonstrate the searched optimal models' actual performance.In this regard,we then retrain the above five optimal models separately and select the optimal modelstructure from them.To avoid over-fitting due to the small training data size,we use contrast change,small-angle rotation,azimuth scale change,and distance scale change to augment the 1190 ISAR images according to the characteristics of ISAR images of space targets.Fig.11 is an example of performing data augmentation(DA)on ISAR images of five kinds of space targets.Simultaneously,to improve the reliability of the verification results and test results,we used the same satellite models to regenerate a set of ISAR images in the same orbit,expanding the amount of verification data and test data to three times the original.Table 1 shows the size of the training set,validation set,and test set corresponding to each type of satellite in the retraining process.

Table 2 Final performance metrics of the eight models.

To perform comparative analysis under the same conditions,we set each model's retraining learning rate to 1×10,the batch size to 32,and the training epoch Nto 100.Therefore,the training iterations of each epoch is 372.Based on the above parameter settings,we retrain the five optimal models.The retraining processes are shown in Fig.12 (a)～(e).Also,to further compare and demonstrate the searched models'classification effect,we train the models of MobilenetV2 and MobilenetV3.There are two different versions of MobileNetV3-MobileNetV3-Small and MobileNetV3-Large.These two versions correspond to models with low and high requirements for computing resources and storage.In order to make the training more adequate,we set the number of training epochs of the MobilenetV2 and MobilenetV3 models to 200.Fig.12(f)～(h) shows the training effects of the MobilenetV2 and MobilenetV3 models.It should be noted that all the data in Fig.12 has been smoothed before drawing.

It can be seen from Fig.12 (a)～(e) that under the condition of iterative training of 100 epochs,the retraining effects of the five optimal models are relatively similar.When the training reaches the 50th epoch,the five models have converged,and the training accuracy of the five models has all reached 100%.The final verification accuracy of 1BlockNet～5BlockNet model is 95.56%,96.30%,95.80%,97.53% and 95.06% respectively.Also,it can be seen from Fig.12 (f),(g),(h) that the training effects of the MobilenetV2 and MobilenetV3 models have both converged after iterative training of 200 Epochs.The MobilenetV2,MobilenetV3-Small,and MobilenetV3-Large models' final verification accuracy is 90.12%,92.60%,and 91.40%,respectively,which are lower than the five optimal models obtained by the search.

Next,we use the test set in Table 1 to test the above models.Fig.13 (a)～(h) shows the eight models' test confusion matrices,respectively.Table 2 shows the final performance metrics of all models.

Table 3 14 kinds of student model structures based on the one-to-one distillation strategy.

Fig.14.Comparison of FSP distillation training effect of the student models under different distillation strategies.

In Table 2,the Macro Average represents the average value of each performance metric.It can be seen from Fig.13 and Table 2 that the model performance between the 1BlockNe～5BlockNet models is relatively similar.From the final performance metrics,the model performance of the 4BlockNet model is the best.Its test accuracy,Macro Average PPV,Macro Average TPR,and Macro Average Fare all 97.8%.In contrast,the model performance of 2BlockNet and 3BlockNet is slightly weaker,and the model performance of 1BlockNet and 5BlockNet is the worst.At the same time,the searched models are compared with the MobilenetV2 and MobilenetV3 models.It can be seen that the optimal search models 1BlockNet～5BlockNet have better model performance than MobilenetV2 and MobilenetV3,which verifies the effectiveness of the method in this paper.

Next,we take the 4BlockNet model as the teacher model and use the FSP distillation method to compress the 4BlockNet model further to obtain the final ultra-lightweight STIIARM.

4.3.Compression experiment of the optimal model based on the FSP distillation method

Before distillation,we need to design a more lightweight student model and then use the 4BlockNet model to guide the student model to train.Next,the student model is designed according to the principle of similar block structure,the same corresponding channel number,and the minimum computational complexity given in Section 3.1.Combining the scope of the hierarchical decomposition search space given in Section 4.2.1,the designed student model has the following characteristics:

(1) Maintain a four-block structure;

(2) The size of all convolution kernels in the student model is set to 3×3;

(3) Each block in the student model contains only one ILB,and the number of IRBs is set to 0;

(4) The SE ratio of each block in the student model is set to 1;

(5) The output filter size of the block without doing distillation is set to 3.

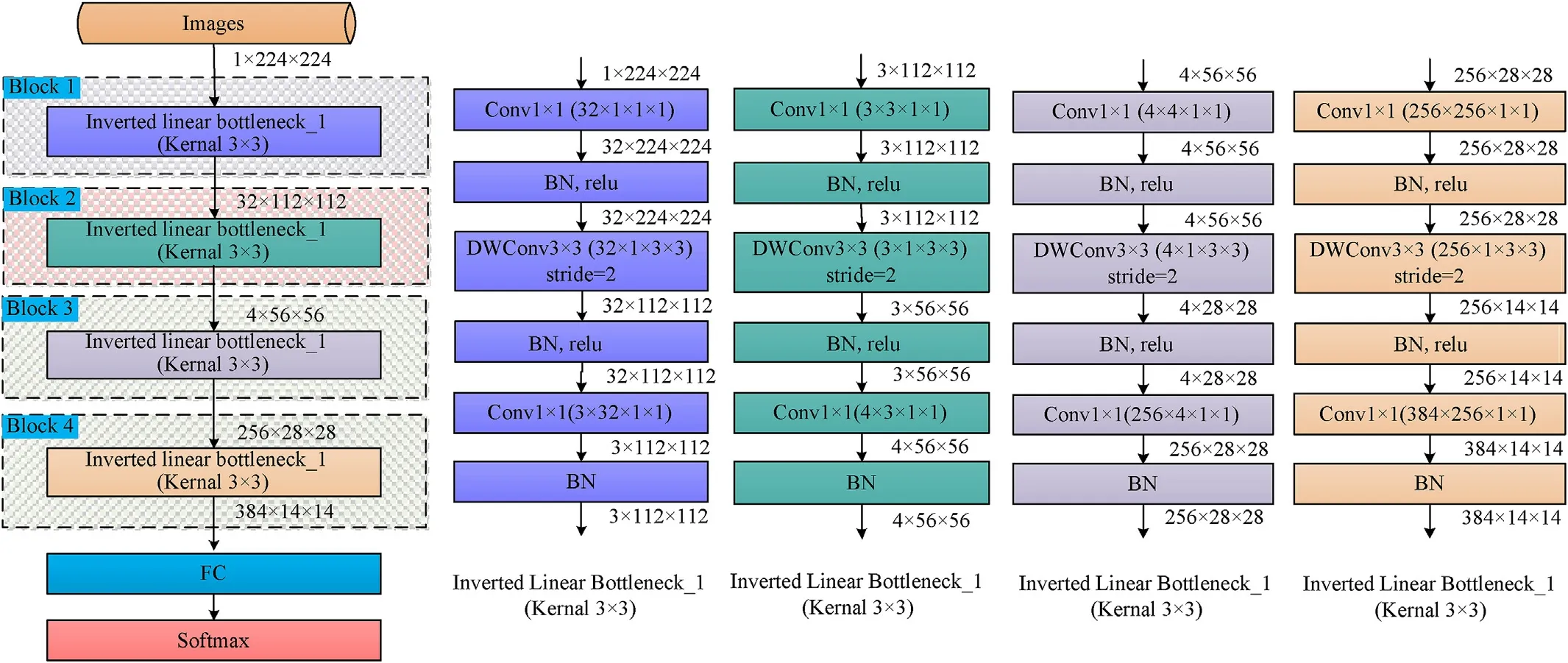
Fig.15.The specific network structure of ultra-lightweight STIIARM.

Fig.16.Test confusion matrix of all models.(a) Test confusion matrix of the ultra-lightweight STIIARM;(b) test confusion matrix of the 4BlockNet model after pruning with a pruning rate of 0.1;(c)test confusion matrix of the 4BlockNet model after pruning with a pruning rate of 0.2;(d)test confusion matrix of the 4BlockNet model after pruning with a pruning rate of 0.3;(e) test confusion matrix of 4BlockNet model after quantization operation.

According to the one-to-one distillation strategy,14 kinds of student model structures meet the above requirements.The computational complexity of each student model and the number of FSP matrices required for KD operation are shown in Table 3.

To ensure that the student model is sufficiently lightweight,we take the computational complexity of the lightweight model MobileNetV2 as the benchmark for student model selection.Considering the MobileNetV2 model's computational complexity is 3,1234,5728.0,we take the seven student models in Table 3 thatmeet the requirements as the candidate models.The seven student models correspond to the distillation strategies of 2→2,3→3,4→4,2&3→2&3,2&4→2&4,3&4→3&4,and 2&3&4→2&3&4,respectively.To further select student models with higher classification accuracy,we train the seven models according to Algorithm 2.The training set,validation set,and test set are consistent with Table 1.

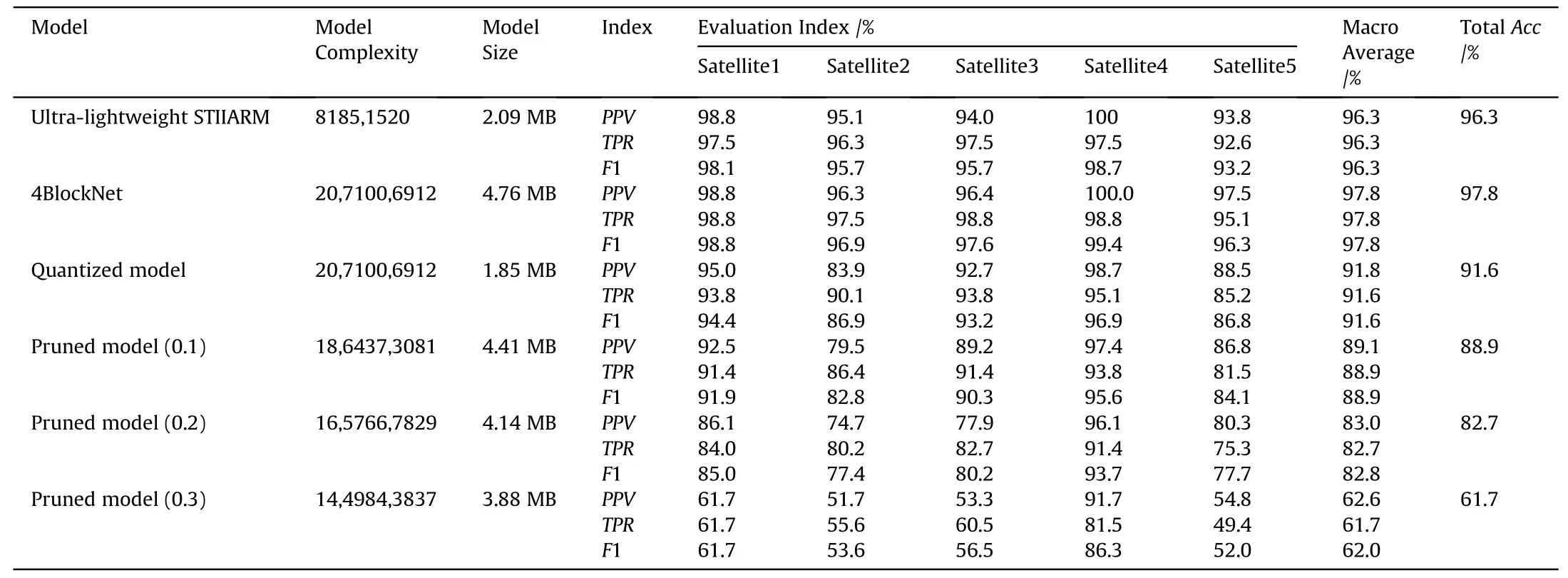
Table 4 Comparison of final test results of the models.

Table 5 Parameters of the virtual machine and Vivox60Pro devices.

It can be obtained that the number of model training generations corresponding to each epoch is 171 times.We use the pretrained 4BlockNet model to guide the student model to perform FSP distillation and compare the model's distillation effect with the direct training effect.Fig.14 shows the FSP distillation process and the direct training process corresponding to the seven student models.

Fig.17.Debugging results of the model on the virtual machine.

It can be seen from Fig.14 that with the increase of training epochs,the training accuracy of the seven student models is continuously improved,and the training cross-entropy loss is continuously reduced.Among them,the student model corresponding to the 2&3&4→2&3&4 distillation strategy has the best FSP distillation training effect.Its verification accuracy and verification cross-entropy loss is 96.54% and 0.1009,respectively.Distillation training effect of student models corresponding to the 2&3→2&3 distillation strategy,3&4→3&4 distillation strategy,and the 3 →3 distillation strategy are the next best.Their verification accuracy is 90.86%,90.62%,and 89.63%,respectively,and the verification cross-entropy loss is 0.2516,0.2733,and 0.2723,respectively.The distillation training effects of student models corresponding to the 4→4 distillation strategy,2→2 distillation strategy,and 2&4→2&4 distillation strategy are relatively low.Their verification accuracy is 81.98%,77.53%,and 76.79%,respectively,and the validation cross-entropy loss is 0.5527,0.7686,and 0.5971,respectively.Therefore,we choose the student model corresponding to 2&3&4→2&3&4 distillation strategy as the final ultra-lightweight STIIARM,and its corresponding network structure is shown in Fig.15.

Next,we use the trained ultra-lightweight STIIARM to classify the test set in Table 1.To prove the superiority of the method proposed in the paper,we compare the test results of the ultralightweight STIIARM with the test results of the pruned and quantified 4BlockNet model.When pruning the model,we use the uniform pruning method [41] to prune the model′s convolutional layer.To compare the model compression effect under different pruning rates,we set the pruning rate of the 4BlockNet model to 0.1,0.2,and 0.3,respectively.When performing model quantization,considering that the model compressed by the post-training quantization way requires inverse quantization in actual use,we choose quantization aware training way [42] for the 4BlockNet model′s quantization operation.We quantize the 4BlockNet model from float 32 to int 8.The test confusion matrix and test results of all models are shown in Fig.16 and Table 4,respectively.

Fig.16 and Table 4 show that the computational complexity and model size of the ultra-lightweight STIIARM are 8185,1520 and 2.09 MB,which are 19,8915,5392 and 2.67 MB less than the teacher model 4BlockNet.It means that the ultra-lightweight STIIARM obtained after distillation is two orders of magnitude lower in computational complexity than the teacher model 4BlockNet,and the model size is only 43.91% of the teacher model 4BlockNet.Simultaneously,the test accuracy,Macro Average PPV,Macro Average TPR,and Macro Average Fof the ultra-lightweight STIIARM all reach 96.3%,which is only 1.5% lower than the teacher model 4BlockNet.From this,we can see that the test results of the ultra-lightweight STIIARM are very close to the 4BlockNet model.Therefore,the FSP distillation method can further obtain an ultralightweight model with lower computational complexity and a smaller model size while retaining the NAS model's high accuracy.

Besides,compared with other models in Table 4,it can be seen that the ultra-lightweight STIIARM has the lowest model computational complexity and the best test effect.Compared with the 4BlockNet model after pruned by 0.3 pruning rate,the computational complexity of the ultra-lightweight STIIARM is reduced by 94.4%,and the testing accuracy,Macro Average PPV,Macro Average TPR,and Macro Average Fhas increased by 34.6%,33.7%,34.6%,and 34.3%,respectively.Compared with the 4BlockNet model after pruning by pruning rate of 0.1,the test result of the ultralightweight STIIARM is improved by more than 7.2%.Compared with the quantified 4BlockNet model,the computational complexity of the ultra-lightweight STIIARM is reduced by 96.05%,and the test accuracy is increased by more than 4.5%.It can be explained that,compared with the pruning and quantification methods of directly compressing the original model,the FSP distillation method can avoid the operation of the model itself and is more suitable for compressing the NAS model.

Fig.18.Deployment results of the model on vivoX60Pro.

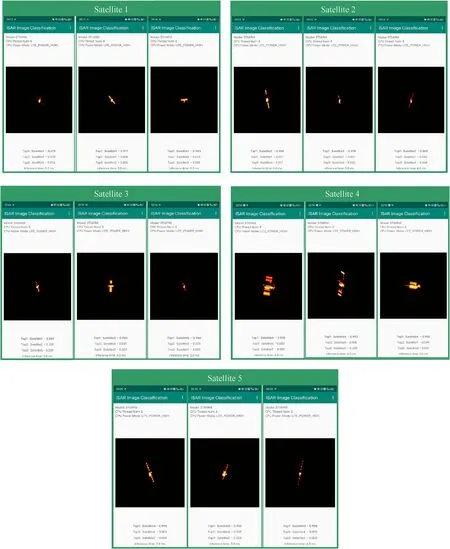
Fig.19.Partial test results of the deployed model.

Finally,we deploy the ultra-lightweight STIIARM on the mobile terminal.The vivoX60Pro mobile device is used as an example during deployment,and the model is debugged on the virtual machine.The virtual machine parameters are shown in Table 5.The debugging results are shown in Fig.17.After the debugging is successful,we deploy the model to the vivoX60Pro mobile device,and the deployment results are shown in Fig.18.Fig.19 shows part of the test results of the deployed model.The test results show that the deployed model's average inference time for the space target ISAR image is 3.3 ms.

5.Conclusions

This paper proposes a novel ultra-lightweight CNN structure design method based on the NAS method and FSP distillation method under the background of space target ISAR image recognition.It completes the automatic construction of ultra-lightweight STIIARM.1.Based on the ILB and IRB,a hierarchical decomposition search space for CNN structure search is constructed;2.Take the model's recognition accuracy and computational complexity as the objective function and constraint.The SA algorithm is used to search for the STIIARM with the highest recognition accuracy in the search space;3.A specific student network model with lower computational complexity than the searched model is designed based on the three principles of similar block structure,the same corresponding channel number,and the minimum computational complexity.Furthermore,based on the FSP distillation method,the student model's guidance training by the searched model is realized,thus obtaining the ultra-lightweight STIIARM with lower computational complexity than the searched model.

5.1.The simulation results show that

(1) The proposed SANSA method can search for the light-weight STIIARM with high recognition accuracy on a common computing platform.When the number of downsampling times is equal to the blocks in the model,the searched 4BlockNet model can achieve the best classification performance.The computational complexity of the 4BlockNet model is 2,071,006,912,and the model size is 4.76 MB.After retraining,the test accuracy,Macro Average PPV,Macro Average TPR,and Macro Average Fof the 4BlockNet model are 97.8%,which is better than MobileNetV2 and Mobile-NetV3 models.

(2) The FSP distillation method can effectively compress the NAS model while retaining its high accuracy.Under the one-toone distillation strategy,the ultra-lightweight STIIARM designed based on the 2&3&4→2&3&4 distillation strategy can achieve the best distillation effect.The calculation complexity of the ultra-lightweight STIIARM is 81851520.0,and the model size is 2.09 MB.Compared with the searched 4BlockNet model,the model computational complexity and model size are reduced by 1,989,155,392 and 2.67 MB,respectively.Also,the ultra-lightweight STIIARM retains the high accuracy of the 4BlockNet model.Its test accuracy,Macro Average PPV,Macro Average TPR,and Macro Average Fis 96.30%,which is better than the 4Blocknet model after pruning or quantization operation.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.