Effect of different geometrical non-uniformities on nonlinear vibration of porous functionally graded skew plates:A finite element study
2022-06-27NaveenKumarSubhaschandraKattimani
H.S.Naveen Kumar,Subhaschandra Kattimani
Department of Mechanical Engineering,National Institute of Technology Karnataka,Surathkal,575025,India
Keywords:Functionally graded material Shear deformation theory Porosity distributions Variable thickness Geometrical skewness Nonlinear free vibration
ABSTRACT This article presents the investigation of nonlinear vibration analysis of tapered porous functionally graded skew (TPFGS) plate considering the effects of geometrical non-uniformities to optimize the thickness in the structural design.The TPFGS plate is analyzed considering linearly,bi-linearly,and exponentially varying thicknesses.The plate's effective material properties are tailor-made using a modified power-law distribution in which gradation varies along the thickness direction of the TPFGS plate.Incorporating the non-linear finite element formulation to develop the kinematic equation's displacement model for the TPFGS plate is based on the first-order shear deformation theory (FSDT) in conjunction with von Karman's nonlinearity.The nonlinear governing equations are established by Hamilton's principle.The direct iterative method is adopted to solve the nonlinear mathematical relations to obtain the nonlinear frequencies.The influence of the porosity distributions and porosity parameter indices on the nonlinear frequency responses of the TPFGS plate for different skew angles and variable thicknesses are studied for various geometrical parameters.The influence of taper ratio,variable thickness,skewness,porosity distributions,gradation,and boundary conditions on the plate's nonlinear vibration is demonstrated.The nonlinear frequency analysis reveals that the geometrical nonuniformities and porosities significantly influence the porous functionally graded plates with varying thickness than the uniform thickness.Besides,exponentially and linearly variable thicknesses can be considered for the thickness optimizations of TPFGS plates in the structural design.
1.Introduction
Functionally graded materials (FGMs) are the class of new unconventional materials with inimitable heterogeneous constituents of materials.FGMs are first proposed by a group of material scientists from Japan[1].FGMs are the amalgamation of two or more materials with a gradation of material properties that varies from one phase(ceramic)to another phase(metal)smoothly.In contrast to composite materials,FGMs have excellent advantages:hightemperature resistance,corrosion resistance,delamination,toughness,and mechanical strength.Applications of FGMs are widely used in civil structures,marine ships,pressure vessels,aerospace,defence,automobile industries,and bio-medical,etc.FGMs are produced by various techniques such as powder metallurgy technique,vapor deposition technique,high-speed centrifugal casting,ultraviolet irradiation process,direct oxidation technique,etc.Besides,due to the fabrication technique's limitations,a generation of porosities cannot be prevented during the production of FGMs structures.In addition,Porosities could occur due to the difference in the two material's solidification temperature [2,3].As a consequence,the presence of porosity can weaken the strength of FGMs.Thus,the effect of porosities on the dynamic characteristics of FGMs plate should therefore be considered.
Many investigators have carried out an extensive analysis of functionally graded (FG) rectangular plate's dynamic characterization with uniform thickness and various solution methodologies for different kinds of FGMs [4-17].Various plate theories have been proposed on the nonlinear vibration analysis by considering FG thin and thick plate's geometrical nonlinearity and the effects of transverse shear deformation for uniform thickness.For example,Huang and Shen [18,19] investigated the nonlinear free vibration and dynamic response of FG rectangular plates with and without piezoelectric actuators subjected to thermal loads.Sundararajan et al.[20] developed nonlinear finite element (FE) governing equations by assuming von Karman's nonlinearity to examine the nonlinear free vibration characteristics of FG rectangular and skew plates with uniform thickness under the thermal environment.Yang et al.[21]presented nonlinear vibration and transient analysis of FG plate with a surface crack exited by transverse force.Yang and Shen[22]investigated free and forced vibration of initially stressed FG plates with uniform thickness in the thermal environment by adopting Reddy's higher-order shear deformation theory(HSDT)in conjunction with von Karman's geometric nonlinearity.Chen et al.[23,24] derived the nonlinear equations of motion for initially stressed and non-uniform initial stresses on FG plates based on classical laminated plate theory (CLPT) to investigate linear and nonlinear frequencies.Woo et al.[25] presented an analytical solution to obtain nonlinear free vibration of FG plates.The governing equations of motion are obtained using von Karman's assumptions for large transverse deflections and mixed Fourier series analysis.Talha et al.[26] investigated the nonlinear free vibration of FG plates by developing nonlinear FE equations based on HSDT associated with Green-Lagrange's nonlinear relations.Alijani et al.[27]studied the nonlinear free vibration of FG rectangular plate coupled with thermal effects by utilizing a multi-modal energy method,pseudo-arc-length,and collocation methods.Malekzadeh et al.[28]proposed the effects of in-plane material gradation.The nonlinear vibration of FG plates with non-varying thickness is investigated for different boundary conditions.Shen et al.[29] investigated the nonlinear vibration of FG graphene reinforced with composite laminated plates exposed to a thermal environment.Parida et al.[30,31] presented the nonlinear free vibration behavior of FG rectangular and skewed plates with an unvarying thickness resting on an elastic foundation by utilizing the HSDT with Green Lagrange's geometric nonlinearity under thermal environments.Tomar and Talha[32]developed a FE formulation for the nonlinear vibration analysis of FG laminated skew plates under a thermal environment.
Recently,theoretical advancements have been attentive to vibration and dynamic characteristics of porous FGMs structures(plates,beams,and shells)for uniform thickness,assuming various porosity distributions.The most recent works on the linear vibration and dynamic analyses to investigate the influence of porosity distributions of porous FG structures with several solution methods are presented by various authors [33-42].Besides,Wang et al.[43,44]presented the nonlinear vibration of porous FG(PFG)plates by adopting a harmonic balance method.Wang et al.[45]continued investigating the nonlinear forced vibration of PFG piezoelectric plates with unvarying thickness.Gupta and Talha [46,47] investigated the nonlinear vibration and stability of FG plates with geometric imperfections and porosity for non-varying thickness in the framework of HSDT.Huang et al.[48] investigated the nonlinear natural frequency and dynamic response of sigmoidal PFG plates with nonlinear elastic boundary conditions.They found that the effect of nonlinear foundation on PFG plates has less impact.Xie et al.[49]explored the nonlinear free vibration of rectangular PFG plates based on the novel energy balance approach in conjunction with von Karman's assumptions and Lagrange's equations to obtain the governing equations of a PFG plate.Kumar et al.[50].Presented the nonlinear vibration and transient responses of PFG skew plates with uniform thickness.
Moreover,the study on the non-uniform thickness of porous FG plates is still an overlooked area.Only a few investigators have attempted to investigate the effects of variable thickness on PFG plates/shells to develop engineering applications in the last few years with several solution methods [51,52].Further,Xu and Zhou[53] investigated the displacements and stress distributions of FG plates with variable thickness.Bouguenina et al.[54] presented a numerical solution to study the effects of thermal buckling of FG plates with varying thicknesses.Thang et al.[55] proposed an analytical approach to study the impact of variable thickness on the behavior of buckling and post-buckling of imperfect FG plates resting on elastic foundations.Lieu et al.[56] developed an isogeometric model to study the free vibration and bending characteristics of in-plane bi-directional FG plates with non-uniform thickness.Chen et al.[57] presented the vibration characteristics of in-plane PFG parallelogram plates with variable thickness using a numerical approach.Minh et al.[58]studied the effects of cracks on FG plate's stability with exponentially varying thickness by adopting HSDT.Kumar et al.[59] developed a model on tapered PFG plates resting on an elastic foundation to investigate a plates' free vibration.Farsadi et al.[60]investigated the nonlinear panel flutter and bifurcation behavior of tapered PFG skew plates,such as skewness and variable thickness.The FG plate's non-uniform thickness has real-world applications in defence,such as bulletproof vests,armour plates,axle housings,and latches.However,landing gear doors,turbine blades,wings,spacecraft truss structures,fuel tanks,electronic components,machine parts,solar panels,and laptop cases are other fields of use.
However,in most of the previous researches,it is seen that the influence of porosity distributions on the nonlinear vibration analysis with two types of geometrical non-uniformities is scarce.For the refinement of the thickness of the porous FG plates,the present research work makes a bridge to introduce the novelty and attain the first attempt at understanding the nonlinear free vibration behavior with variable thickness and geometrical skewness for the products used in the defence,energy,aerospace,automotive,and civil fields.In this regard,this study presents the primary effort at evaluating the effects of porosity distributions coupled with geometrical skewness and various types of variable thickness on the nonlinear vibration analysis of tapered porous functionally graded skew(TPFGS)plates.To this end,the present article intends to establish a nonlinear FE model in conjunction with von Karman's geometric nonlinearity considering the porosities with the aid of Hamilton's principle under the framework of FSDT to fill the research gap.The large amplitude free vibrations of the TPFGS plate are evaluated by the direct iterative method.The effective material properties of the TPFGS plate are computed using modified powerlaw distribution.Further,the research focuses on the influence of the porosity distributions and the geometric non-uniformities such as skewness and various kinds of variable thickness,i.e.,linearly,bilinearly,exponentially varying thickness.Besides,the influence of taper ratio,skewness,porosity distributions,gradation,and boundary conditions affecting the plate's structural behavior is investigated in detail.
2.Problem description
2.1.TPFGS plate geometry
The schematic diagram of the TPFGS plate is depicted in Fig.1.The dimensional parameters referred to a Cartesian coordinate with the x,y,and z coordinate axes spanning its length a,width b,and tapered thickness h(x,y).The geometrical skewness of the TPFGS plate is measured by rotating the coordinate y at an angle Φ called the skew angle.The TPFGS plate consists of different types of variable thickness viz.linearly (h (y)),bi-linearly (h (x,y)),and exponentially (h (y)) variable thickness as shown in Fig.1 (a)-(c).Where,h is a function of both x and y coordinates for bi-linearly variable thickness,while h is a function of the only y coordinate for linearly and exponentially variable thicknesses.
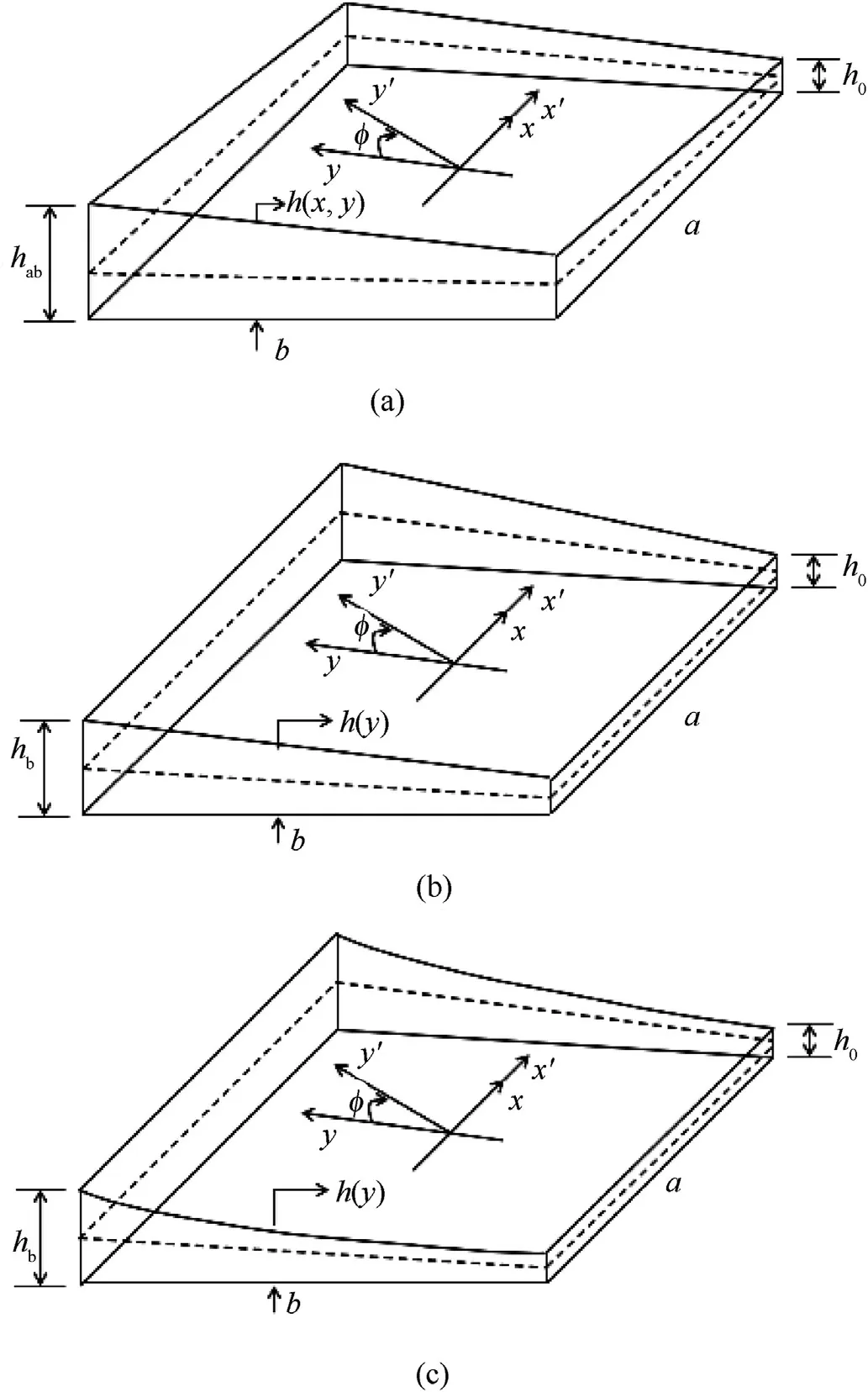
Fig.1.The geometry of the TPFGS plate.(a) Bi-linearly variable thickness,(b) Linearly variable thickness,and (c) Exponentially variable thickness.
2.2.Material properties
The TPFGS plate consists of two isotropic and homogeneous materials,metal and ceramic.The volume fraction of the ceramic material constituent (V) changes continuously in the thickness direction.i.e.,z-axis.The plate's top surface is solely ceramic(z=h(x,y)/2),and the bottom surface is solely metal(z=-h(x,y)/2),as depicted in Fig.1.The appearance of porosity distributions during the fabricating process of a functionally graded skew (FGS) plate is modeled by adopting various mathematical models for distributing the properties.The present analysis emphasizes three types of TPFGS plates viz.ideal (without porosity),evenly distributed,and centrally distributed porous functionally graded skew(PFGS)plates,as shown in Fig.2.In the ideal FGS plate,the plate is assumed to have no pores.As a result,the weight and stiffness of the FGS plate remain constant,as shown in Fig.2 (a).Whereas,in the evenly distributed porosity(P),all the pores are presumed to be uniformly distributed across the TPFGS plate thickness.Hence,the plate's weight and stiffness reduce abruptly,as shown in Fig.2(b).Besides,in centrally distributed porosity (P),all the pores are assumed to be unevenly proportionally distributed across the plate's thickness.Therefore,the weight and stiffness reduce steadily,as shown in Fig.2(c).

Fig.2.Cross-section of the TPFGS plate with the distribution of the porosities.(a)Ideal FGS plate(b)Evenly distributed porosity(Pe)and(c)Centrally distributed porosity(Pc).
The effective material properties of the TPFGS plate(P(z))are young's modulus(E(z)),the density(ρ(z)),and the Poisson's ratio(ϑ(z))at any point in the plate are determined by employing the modified power-law distribution method[61]by using Eq.(1).
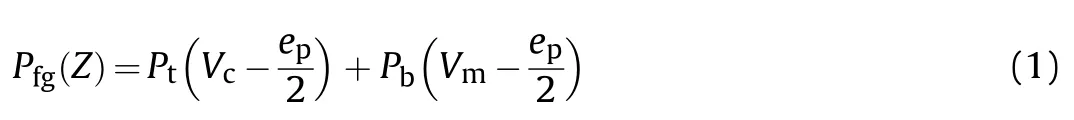
P(z) is the effective material properties along the thickness direction,Pand Pare material properties of ceramic and metal,respectively.Vand Vindicate volume fractions of the ceramic and metal,respectively.e(e<<1)is the porosity parameter index and which is zero(e=0)for an ideal(without porosity)FGS plate.The sum of volume fractions of the ceramic and metal is always unity,and the equation for the volume fraction of the ceramic is as follows:

Where m indicates the volume fraction grading index,it is a positive real number.Z is the distance normal to the mid-plane of the TPFGS plate(h(x,y)/2≤z≤-h(x,y)/2).If m is equal to zero,then the plate becomes a fully ceramic isotropic plate while it becomes a fully metal isotropic plate for the greater values of m (say 100).From Eqs.(1)and(2),the generalized effective material properties of the TPFGS plate [62] for different porosity distributions can be obtained as follows:

2.3.Variable thickness
(a) Bi-linearly variable thickness(h(x,y)):If the non-uniformity of thickness changes in both the directions,i.e.,x-and y-directions of the TPFGS plate as depicted in Fig.1(a),i.e.,taper ratio's β=χ≠0.Then the function for the bi-linearly variable thickness (h (x,y)) varies in both x and y directions can be stated as follows:
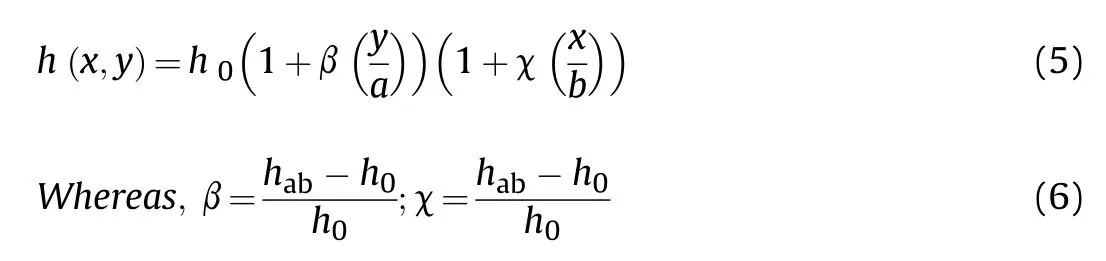
Where β and χ are taper ratios in the y and x directions,respectively;his the initial thickness of the bi-linearly tapered PFGS plate;his the plate's maximum thickness varies in both x and y directions,and x/a and y/b are the dimensionless parameters.
(b) Linearly variable thickness (h (y)):If the non-uniformity of thickness is considered only in the y-direction as shown in Fig.1(b),i.e.,taper ratio β≠0,and χ=0.Then the function for linearly variable thickness h (y) in the y-direction can be expressed as follows:

Where β is the taper ratio in y-direction;his the initial thickness of linearly tapered PFGS plate;his the maximum thickness of the TPFGS plate,which varies in y-direction,and y/b is the dimensionless parameter.
(c) Exponentially variable thickness (h(y)):If the non-uniformity of thickness varies exponentially in the y-direction as represented in Fig.1(c),i.e.,taper ratio β≠0,and χ=0.Then,the function for exponentially variable thickness h(y)in the ydirection can be expressed as follows:

Where β is the taper ratio in y-direction;his the initial thickness of linearly tapered PFGS plate;his the maximum thickness of the TPFGS plate,which varies in y-direction,and y/b is the dimensionless parameter.
2.4.Constitutive equations
The constitutive equations for the TPFGS plate can be articulated as follows [63]:
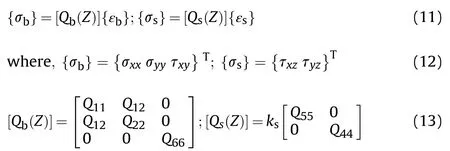
The elastic constants appearing in Eq.(13)can be expressed as:

Where,[Q(Z)]and[Q(Z)]are the elastic coefficient matrices of the TPFGS plate and are the function of z-coordinate;{σ}and {σ}are the stress tensors;{ε}and {ε}are the in-plane transverse normal strain and the transverse shear strain,respectively;kis a shear correction factor.The value of the shear correction factor is taken as π/12.
2.5.Displacement equations
The plate model involved in the current analysis is developed using the FSDT in conjunction with von Karman stain-displacement geometric nonlinearity [64].The displacement components u,v,and wat any point in the overall plate along x,y,and z coordinate axes,respectively,can be expressed as

Where uand vare the translational displacements along the xand y-coordinates,whereas wis the transverse displacements along the z-coordinate at any point(x,y,z)in the plate.θandθare the corresponding generalized rotations about the y-axis and xaxis,respectively.
Using Eq.(15)and von Karman's nonlinear strain-displacement relations[65],the strain-displacements relations can be written as follows:
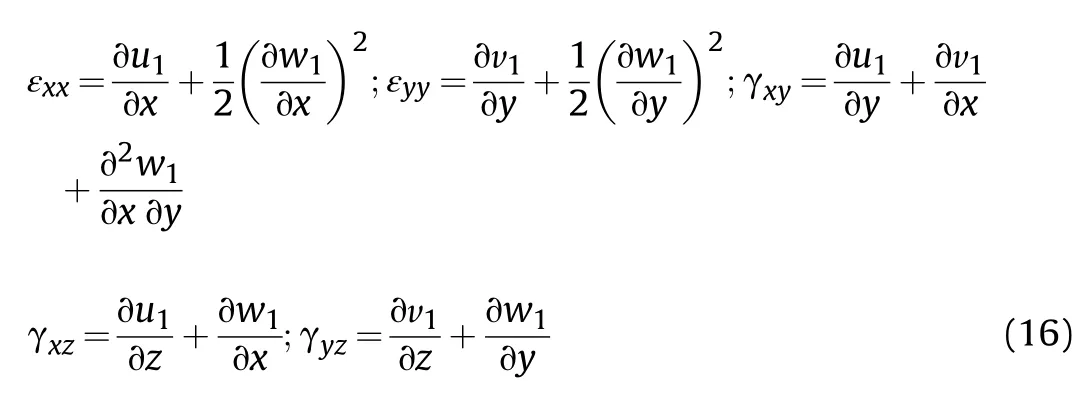
Whereas,Eq.(16) can be written as

The terms εand εappearing in Eq.(17) are the linear and nonlinear strains,respectively.
Substituting Eq.(15) into Eq.(16) gives

The in-plane strain vectors and the transverse shear strain vectors at any point in the TPFGS plate can be expressed as follows:

Table 1 Comparison of the square isotropic tapered plate with various boundary conditions.

Table 2 Comparison of fundamental frequency for a skew plate with SSSS boundary condition.
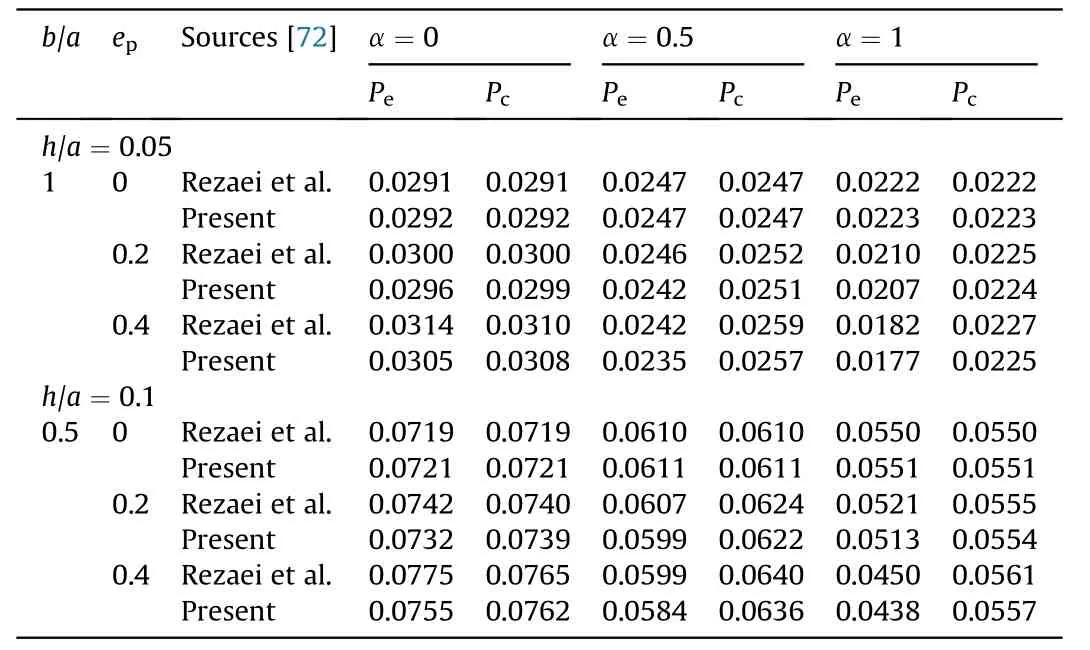
Table 3 Comparison of fundamental natural frequency for different porosity parameter index for SSSS square Al2O3/Al porous FG plate.
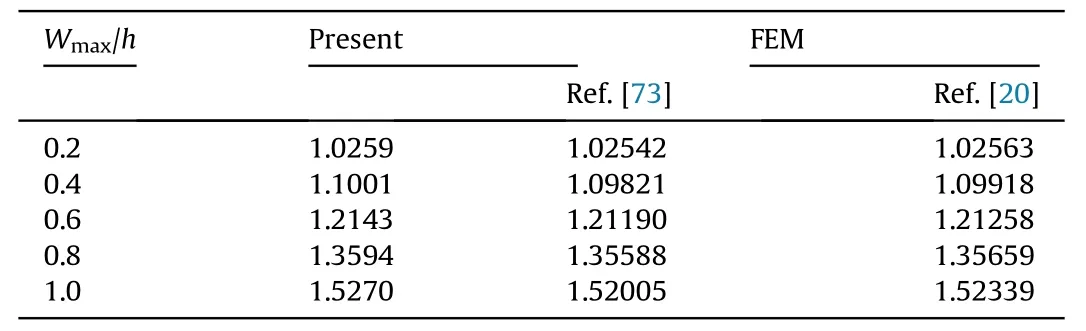
Table 4 Comparison study of nonlinear frequency ratio of a simply supported isotropic plate(a=b=1,a/h=1000).

Where,the terms {ε},{ε},{ε},{ε}and {ε} appearing in Eq.(19) are the generalized strain vectors and are obtained as follows:
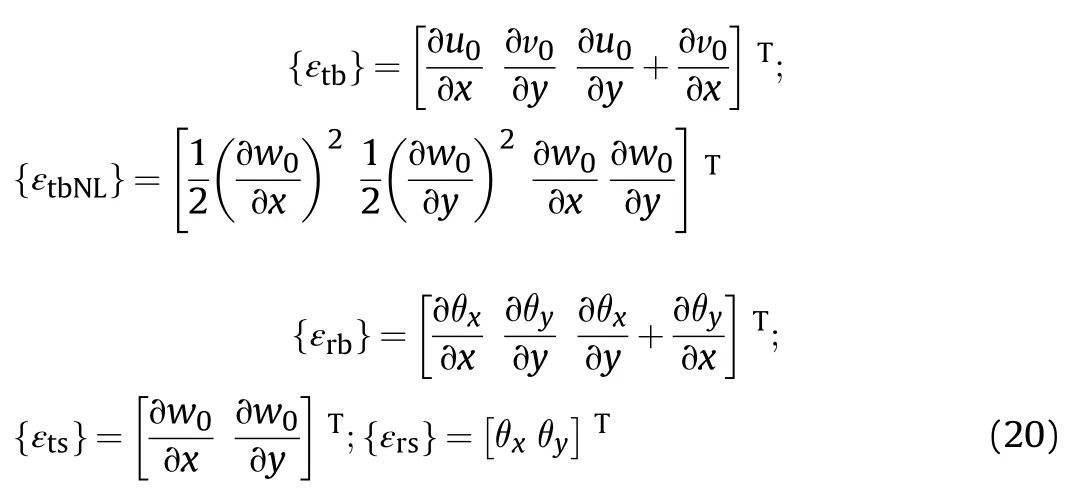
2.6.Equation of motion
Employing Hamilton's principle [66],the first variation of totalpotential energy and kinetic energy of the overall TPFGS plate is derived,and the governing equation of motion of the TPFGS plate is obtained as follows:
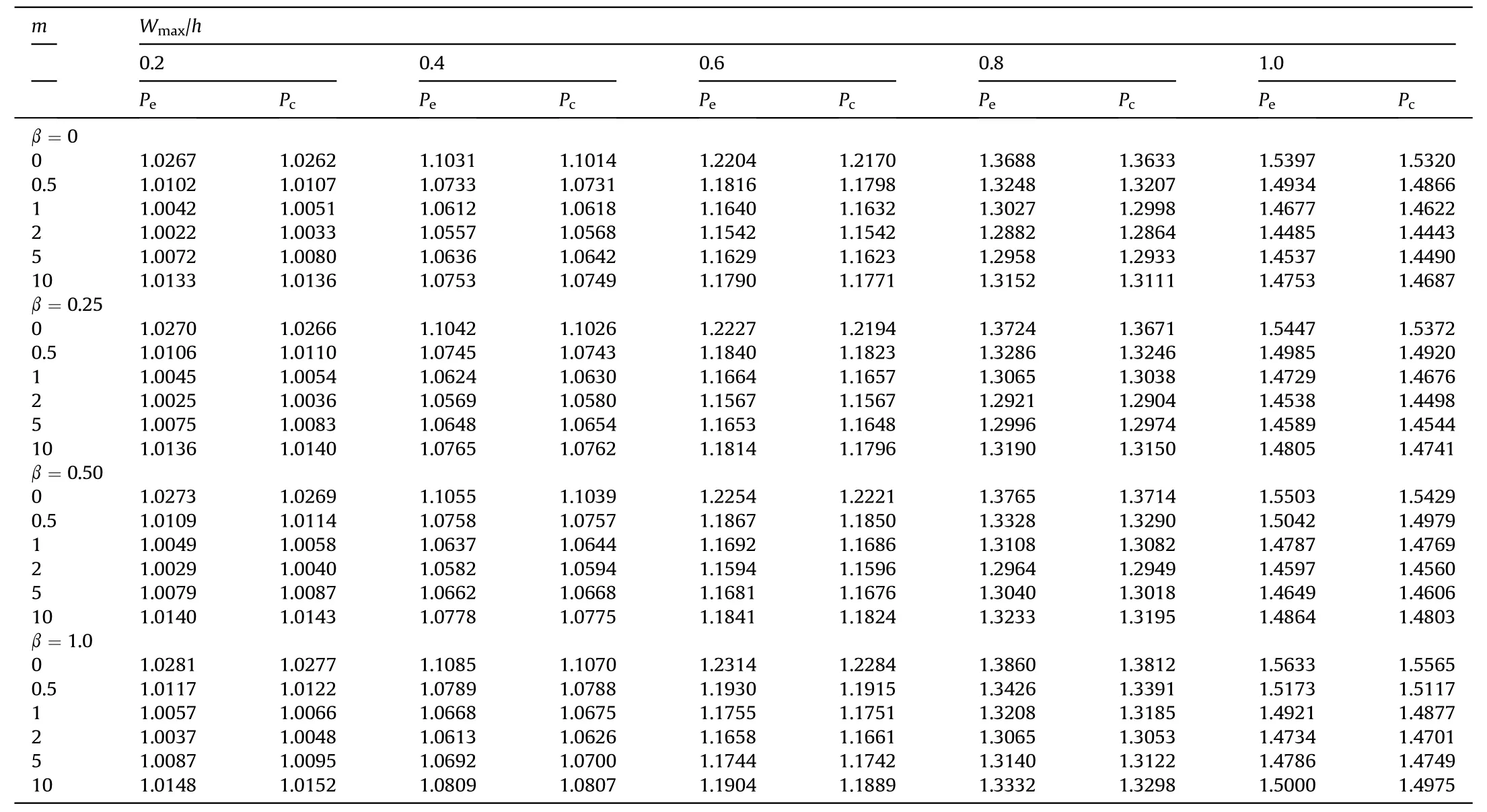
Table 5 Effect of volume fraction index on the NFR(ωnl/ω)of linearly variable thickness Si3N4/SUS304 TPFGS plate for the different taper ratio(β).(a/b=1,h0=1/10,ep=0.1,Φ=0°,χ=0,and SSSS).
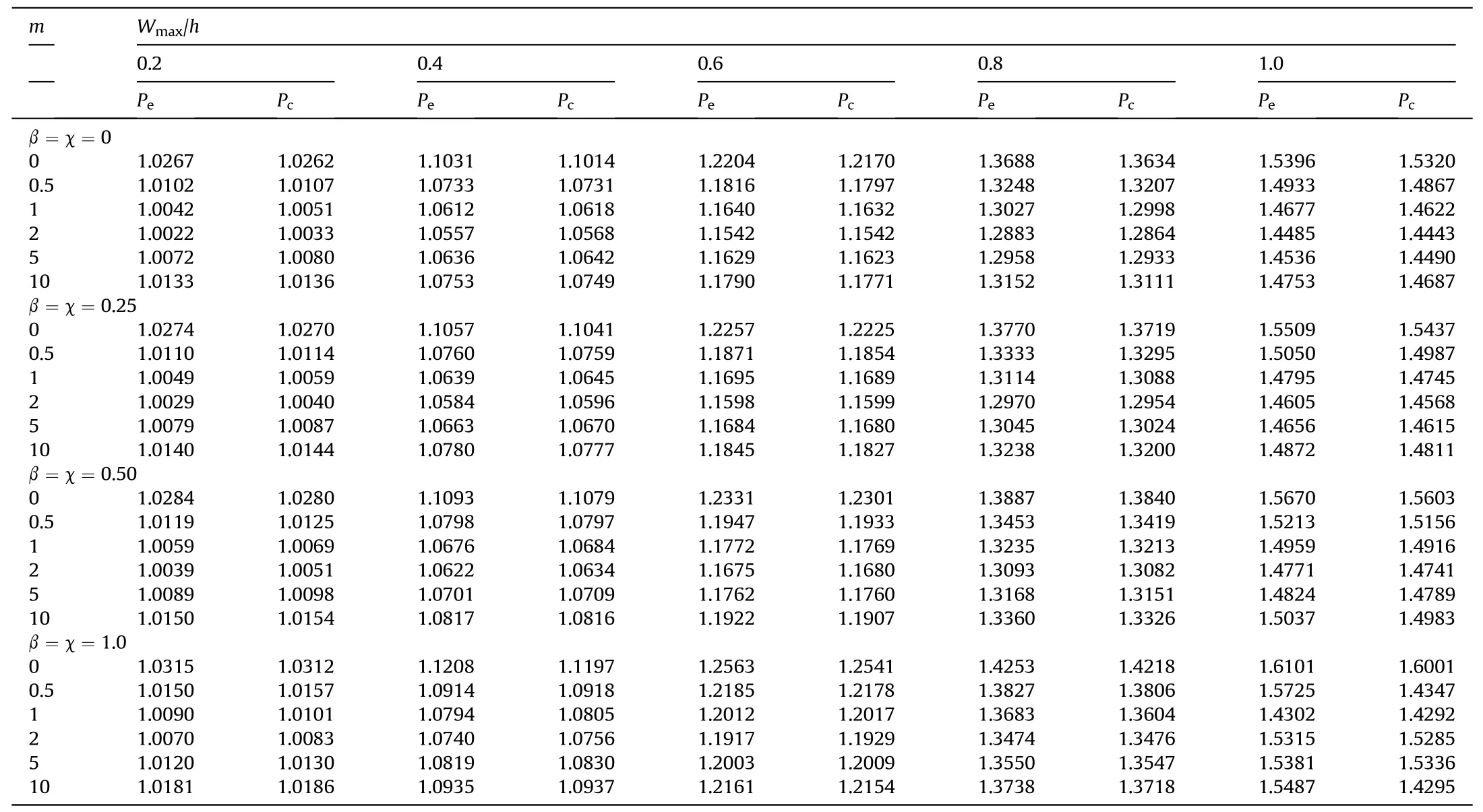
Table 6 Effect of volume fraction index on the NFR(ωnl/ω)of bi-linearly variable thickness Si3N4/SUS304 TPFGS plate for the different taper ratio(β=χ).(a/b=1,h0=1/10,ep=0.1,Φ=0°,and SSSS).

Table 7 Effect of volume fraction index on the NFR(ωnl/ω)of exponentially variable thickness Si3N4/SUS304 TPFGS plate for the different taper ratio(β).(a/b=1,h0=1/10,ep=0.1,Φ=0°,χ=0,and SSSS).

Where {F}={0 0 p}is externally applied traction acting over a surface area;p is the transverse load,ρ is the plate's mass density,and δ is the symbol that describes the first variation.
2.7.Nonlinear finite element (FE) formulation
The nonlinear FE model of the TPFGS plate is discretized using eight noded iso-parametric quadrilateral elements with five degrees of freedom [50,67].Three translational (u,v,and w) and two rotational (θandθ)) for each node.The generalized displacement vectors{d}and{d}are associated with i(i=1,2,3,…,8) node of an element can be written as follows:
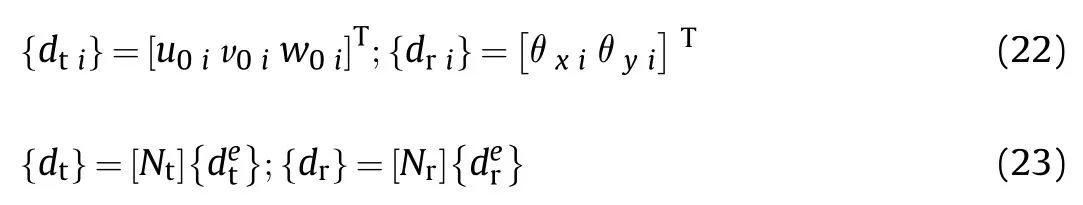


Now,from Eqs.(19) and (23),the generalized nonlinear strain vectors at any point within an element are obtained as follows:

In which,[ß],[ß],[ß],[ß],[ß]and[ß]are the generalized nodal strain displacement matrices demonstrated in Appendix-A.On replacing the terms of Eq.(21) with Eqs.(11),(19) and (25),and applying the principle of total potential energy,i.e.,δT=0,and simplifying,the elemental equations of motions for the TPFGS plate are obtained as follows:
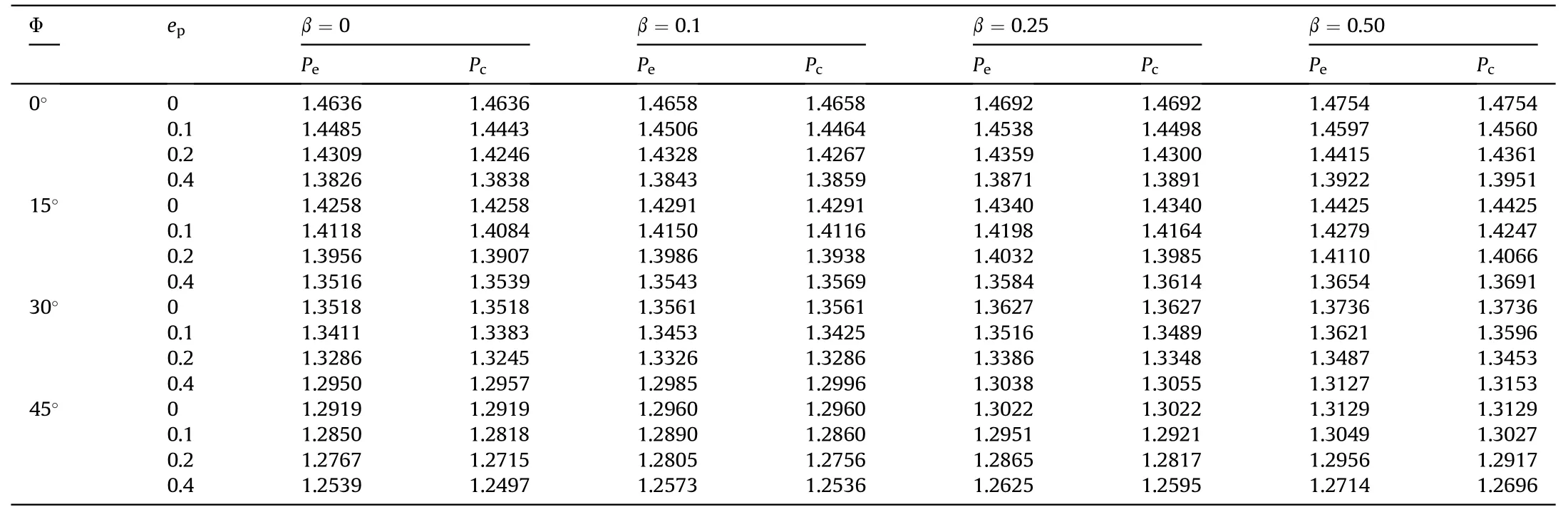
Table 8 Effect of porosity parameter index on the NFR (ωnl/ω) of linearly variable thickness Si3N4/SUS304 TPFGS plate for the different taper ratio (β) and skew angle (Φ).(a/b=1,h0=1/10,m=2,Wmax/h=1.0,χ=0,and SSSS).

Table 9 Effect of porosity parameter index on the NFR(ωnl/ω)of bi-linearly variable thickness Si3N4/SUS304 TPFGS plate for the different taper ratio(β=χ)and skew angle(Φ).(a/b=1,h0=1/10,m=2,Wmax/h=1.0,and SSSS).

Table 10 Effect of porosity parameter index on the NFR(ωnl/ω)of exponentially variable thickness Si3N4/SUS304 TPFGS plate for the different taper ratio(β)and skew angle(Φ).(a/b=1,h0=1/10,m=2,Wmax/h=1.0,χ=0,and SSSS).

Table 11 Effect of thickness-to-length ratio(a/h0)on the NFR(ωnl/ω)of linearly variable thickness Si3N4/SUS304 TPFGS plate for the different taper ratio(β)and skew angle(Φ).(a/b=1,m=2,ep=0.1,Wmax/h=1.0,χ=0,and SSSS).

Table 12 Effect of thickness-to-length ratio(a/h0)on the NFR(ωnl/ω)of bi-linearly variable thickness Si3N4/SUS304 TPFGS plate for the different taper ratio(β=χ)and skew angle(Φ).(a/b=1,m=2,ep=0.1,Wmax/h=1.0,and SSSS).
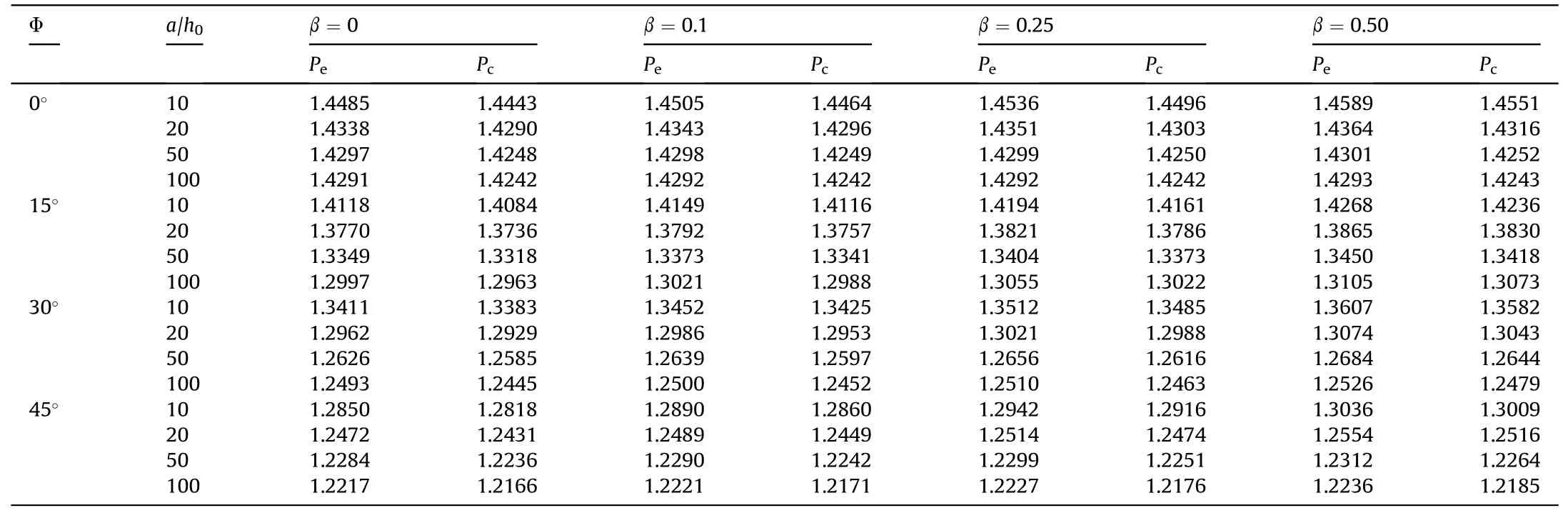
Table 13 Effect of thickness-to-length ratio(a/h0)on the NFR(ωnl/ω)of exponentially variable thickness Si3N4/SUS304 TPFGS plate for the different taper ratio(β)and skew angle(Φ).(a/b=1,m=2,ep=0.1,Wmax/h=1.0,χ=0,and SSSS).
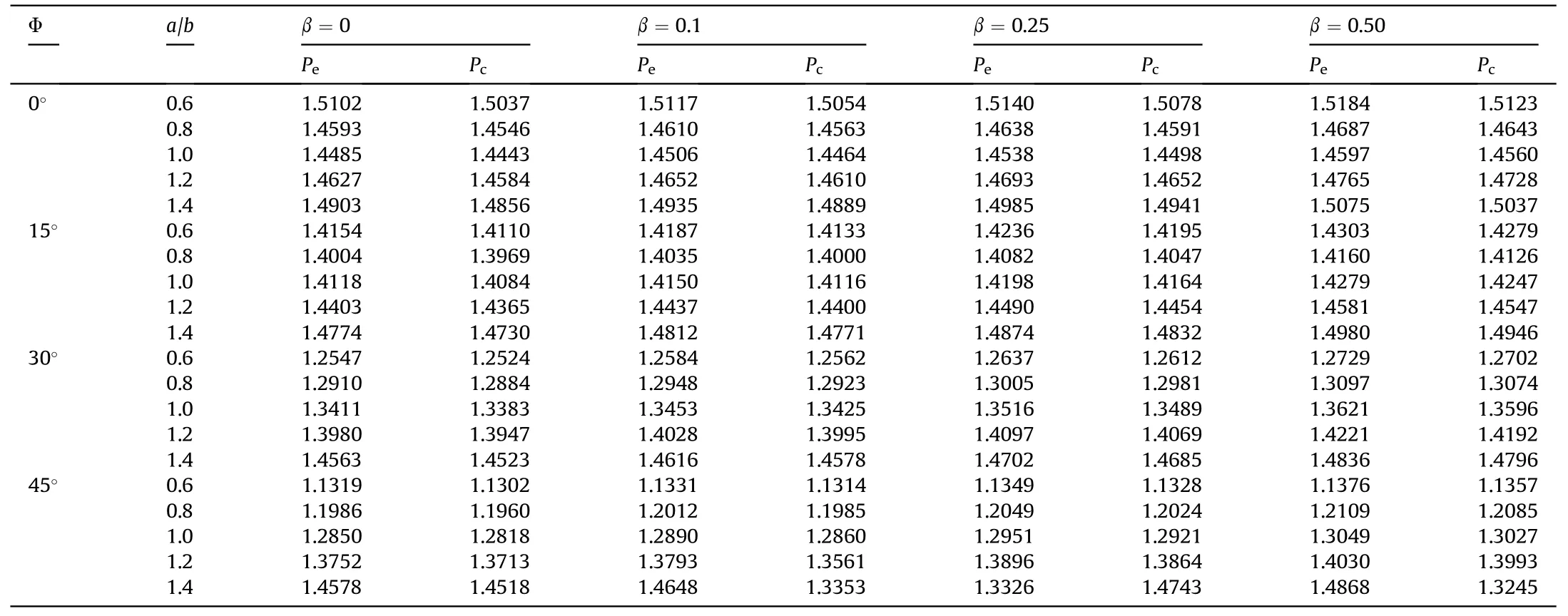
Table 14 Effect of aspect ratio (a/b) on the NFR (ωnl/') of linearly variable thickness Si3N4/SUS304 TPFGS plate for the different taper ratio (β) and skew angle (Φ).(h0=1/10,m=2,ep=0.1,Wmax/h=1.0,χ=0,and SSSS).
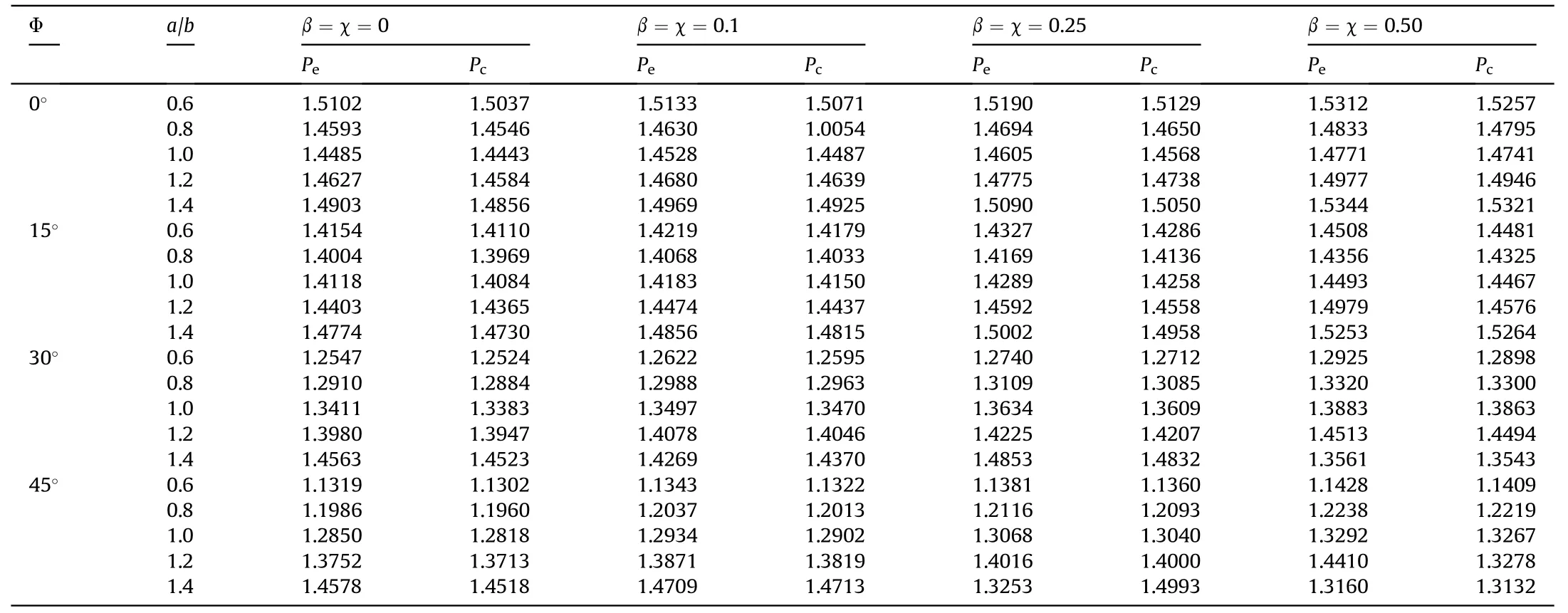
Table 15 Effect of aspect ratio(a/b)on the NFR(ωnl/ω)of bi-linearly variable thickness Si3N4/SUS304 TPFGS plate for the different taper ratio(β=χ)and skew angle(Φ).(h0=1/10,m=2,ep=0.1,Wmax/h=1.0,and SSSS).



The stiffness matrices evolved in Eq.(28)along with the various rigidity matrices and vectors appearing in the elemental matrices are exclusively presented in Appendix-B.
3.Skew boundary transformation
In order to impose boundary conditions on the skew edges ofthe TPFGS plate [62],it is essential to transform the Cartesian coordinate's axes along the x'-,y'-directions,as shown in Fig.1.Therefore,the generalized displacement vectors of a point resting on the skew edge is transformed as follows:

Table 16 Effect of aspect ratio(a/b)on the NFR(ωnl/ω)of exponentially variable thickness Si3N4/SUS304 TPFGS plate for the different taper ratio(β)and skew angle(Φ).(h0=1/10,m=2,ep=0.1,Wmax/h=1.0,χ=0,and SSSS).

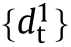

For a given node,the transformation matrices that act on the translational [T]and rotational [T]degrees of freedom along the main diagonals can be written as follows:

As a result,from these transformations,the transformed stiffness and mass matrices yields as follows:

Finally,Eqs.(26) and (27) are condensed to obtain the more generalized form as [50]:



Eq.(33) presents the nonlinear FE model for the TPFGS plate.Further,to find the eigenvalues and eigenvectors of the plate,Eq.(33)can be reorganized as follows:

Where,ω and Xare the fundamental natural frequency and eigenvector of the TPFGS plate,respectively.The fundamental nonlinear frequency-amplitude relationship is computed from Eq.(35)using a direct iterative method [20,68] in association with nonlinear FE formulations.
The boundary conditions on the skew edges of the transformed axes of the TPFGS plate are expressed as follows:
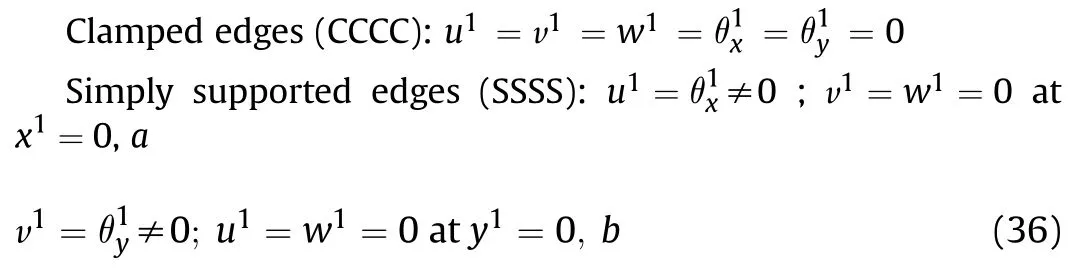
4.Solution methodology
The eigenvalue formulation is used to solve the vibration problems,while the nonlinear eigenvalue problems of the TPFGS plate are solved using a direct iterative approach[50].To begin,Eq.(35)is used to extract the linear eigenvalue and eigenvectors from the global mass and stiffness matrices by ignoring nonlinear stiffness matrices using a standard eigenvalue extraction algorithm.The normalised eigenvector is then scaled up to the amplitude ratio after normalising the mode shape vector.As a result,the desired value must equal the maximum displacement values.The initial vector is thus extracted.The initial nonlinear vector is then computed by numerical integration of the nonlinear stiffness matrices,and the nonlinear eigenvalues and corresponding eigenvectors are then solved.These steps are repeated until the nonlinear frequency,and its mode shape converge at the rate defined by
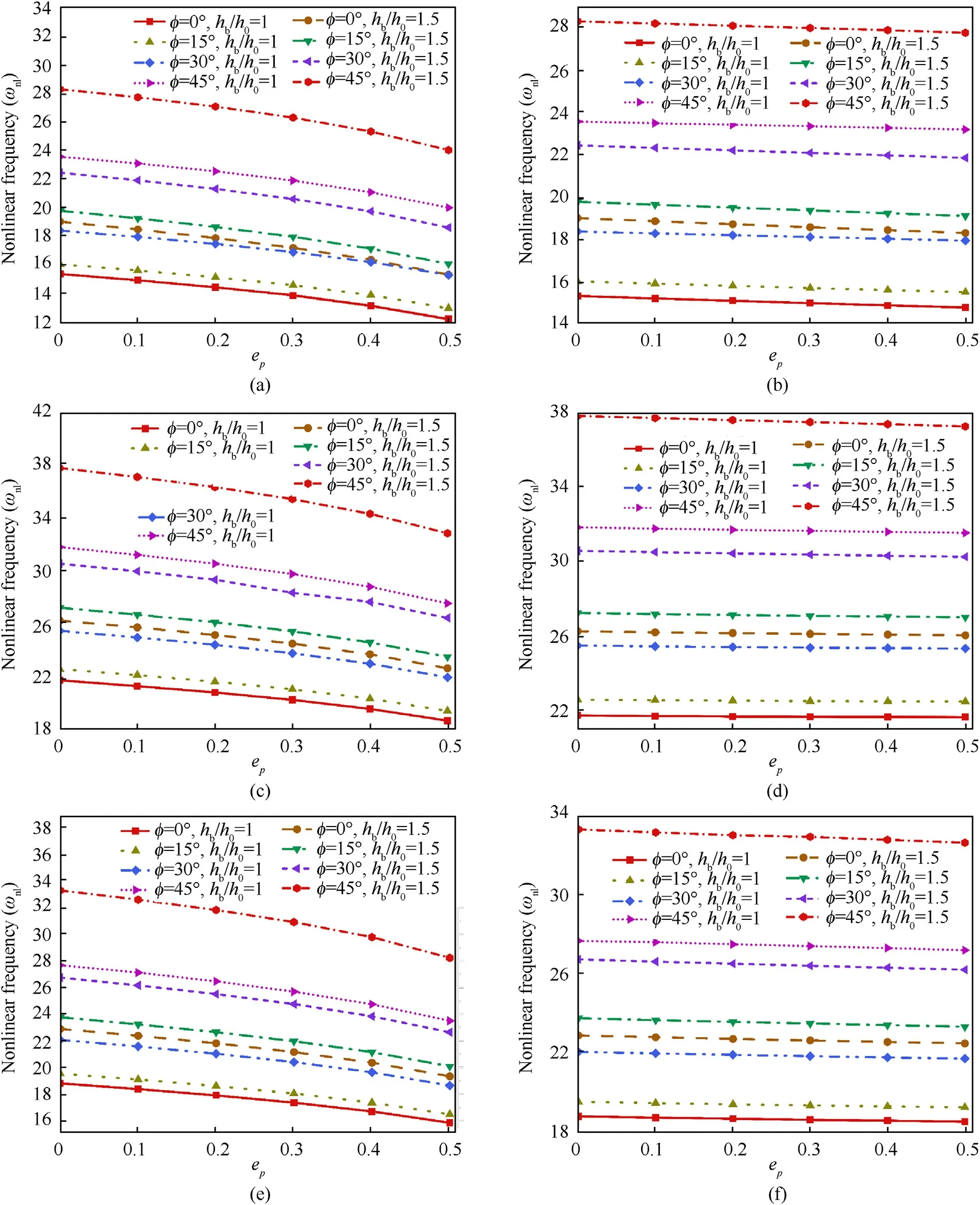
Fig.3.Effects of taper ratio and porosity parameter index on the NFP for the Linearly Variable thickness of the TPFGS plate for different porosity distributions and boundary conditions (h0=1/10,a/b=1,and m=2) (a) Pe,SSSS,(b) Pc,SSSS,(c) Pe,CCCC,(d) Pc,CCCC,(e) Pe,SCSC,and (f) Pc,SCSC.

The suffix itr denotes the number of iterations.
5.Results and discussions
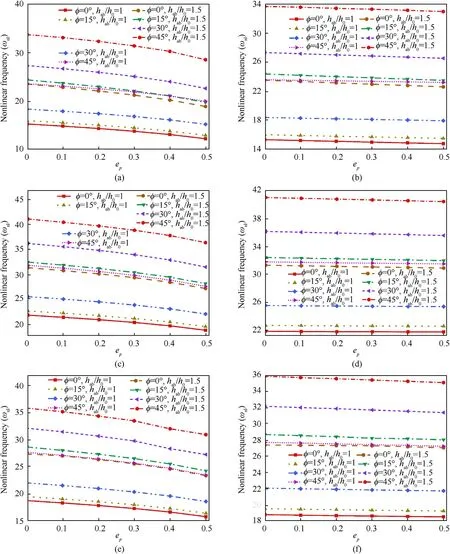
Fig.4.Effects of taper ratio and porosity parameter index on the NFP for the Bi-linearly Variable thickness of the TPFGS plate for different porosity distributions and boundary conditions (h0=1/10,a/b=1,and m=2) (a) Pe,SSSS,(b) Pc,SSSS,(c) Pe,CCCC,(d) Pc,CCCC,(e) Pe,SCSC,and (f) Pc,SCSC.
The TPFGS plate made of SiN/SUS304 is considered to investigate the porosity distribution's influence coupled with geometrical non-uniformities on the nonlinear free vibrations.The plate's top surface is tapered,consisting of ceramic material,while its bottom metallic surface is flat.There is a gradation of these materials between the tapered top surface and the bottom surface,including porosities.The nonlinear FE formulation proposed in sections-2 and 3 is adopted in this regard.Further,numerous examples are demonstrated to study the significance of porosity distributions,porosity parameter,and volume fraction index,aspect ratio,and span ratio for various skew angles and the taper ratio of different types of variable thickness on the large amplitude free vibrations of the TPFGS plate.
The TPFGS plate consists of SiN/SUS304 material with the properties of Young's modulus (E),and density (ρ) for the ceramic material (SiN) are 322.27×10N/mand 2370 kg/m,respectively,and for the metal(SUS304)207.79×10N/mand 8166 kg/m,respectively,are considered.The Poisson's ratio(ϑ)for both the constituent materials is assumed to be 0.280.

Fig.5.Effects of taper ratio and porosity parameter index on the NFP for the exponentially Variable thickness of the TPFGS plate for different porosity distributions and boundary conditions (h0=1/10,a/b=1,and m=2) (a) Pe,SSSS,(b) Pc,SSSS,(c) Pe,CCCC,(d) Pc,CCCC,(e) Pe,SCSC,and (f) Pc,SCSC.
5.1.Verification and comparison
This section is devoted to verifying the proposed nonlinear FE formulation.The fundamental natural frequencies of a square isotropic tapered plate are compared with the earlier results[59,69,70]for the span ratio(a/h)100,10,and 5,and the taper ratio for linearly varying thickness(β)0.25,0.50,and 1.0.The mesh size of [8×8] is used based on a progressive mesh refinement.The obtained results in Table 1 display excellent agreement with the reference literature [59,69,70].For further validation,the study is extended for the fundamental natural frequency of a square isotropic skew plate with skew angles of 0,15,30,and 45with SSSS boundary condition for the thickness ratio a/h=10 and 5.It may be noted from Table 2 that there is a good agreement with the results of Liew et al.[71].Also,the dimensionless fundamental frequencies parameter for PFG plates are calculated and matched with the results reported in the literature by Rezaei et al.[72] for the AlO/Al PFG plate with SSSS boundary condition for different volume fraction (m) and porosity parameter index (e).Table 3 witnesses that the present results agree very well with published results for both evenly distributed(P)and centrally distributed(P)porosities with reference [72].The nonlinear frequency to linear frequency ratios (NFR)(ω/ω)for various amplitude ratios W/h are validated with the results reported by Balamurugan et al.[73]and Sundararajan et al.[20] and noticed that an excellent agreement with the present nonlinear FE model for a simply-supported isotropic plate as depicted in Table 4.
The FE formulation derived in the present study is used for the parametric studies on porosity distribution's influence on TPFGS plates with variable thickness and skewness.The mesh size[8×8]used for the validation is adopted to extract all parametric results.
5.2.Numerical results
This section presents a study on the nonlinear frequency ratios(NFR) (ω/ω) of the TPFGS plate with geometrical skewness for different taper ratios of various non-uniform thicknesses such as linear,bi-linear,and exponentially varying thicknesses.Tables 5-7 present the NFR for different taper ratios for each type of variable thicknesses and the plate's porosity distributions.The influence of a porosity distributions is computed for a different values of the volume fraction index (m=0,0.5,1,2,5,10).The taper ratios for both the linearly varying and exponentially varying thickness is β=0,0.25,0.50,1.0 meanwhile,the taper ratio for bi-linearly varying thickness is β=χ=0,0.25,0.50,1.0.A comparative study of two different types of porosity distributions Pand Pis presented for the plate edge supported by SSSS boundary conditions.It is depicted from the results that with an increase in the volume fraction index(m)for both Pand P,the NFR decreases till m=2,whereas the trend reverses from m=5.The same trend is noticed for uniform plate thickness and all variable thickness types irrespective of taper ratios and porosity distributions.It may be due to the decrease in ceramic composition with an increase in the volume fraction index,leading to a decrease in the plate's stiffness,and the frequency is proportionally dependent on it.As a result,a rapid decrease in the linear frequency is observed for higher volume fraction index values,which leads to the increase in the difference between nonlinear frequency to linear frequency.Hence,the NFR increases for higher values of volume fraction index.
Further,the NFR increases with an increase in the taper ratio.It can be seen from Tables 5-7 that with an increase in the taper ratio,the degree of hardening nonlinearity increases.Consequently,the amplitude ratio significantly affects the NFR for different values of the taper ratios.Analogously,for a given value of m,the influence of different types of variable thickness on NFR follows the trend as exponentially variable thickness <linearly variable thickness <bilinearly variable thickness.An increase in the taper ratio increases the plate's stiffness,which results in higher nonlinear frequency.
Additionally,the effect of porosity distribution on the NFR follows the trend as centrally distributed porosity (P) <evenly distributed porosity (P),irrespective of different types of porosity distributions and taper ratio.The presence of porosities in the gradation region has significantly reduced the stiffness and weight of the plate.Hence,it has considerably less impact on the NFR.
The effect of geometrical skewness and porosity parameter on the NFR for different types of variable thickness of the TPFGS plate is also studied.Tables 8-10 depict the results of the NFR for different skew angles,porosity parameter index,taper ratio,and various types of variable thickness of the plate.A comparative study of Pand Ptype of porosity distributions with geometrical skewness for several inconstant thickness types is presented.As expected,with an increase in the porosity parameter index for both Pand P,the NFR decreases irrespective of the taper ratio,skew angle,and the type of variable thickness.It can be due to the reduction in the TPFGS plate's stiffness on which the frequency depends proportionally.This kind of impulsive behavior arises because of non-dimensionalized parameters.
Further evaluation reveals that irrespective of the porosity distributions,taper ratio,and type of variable thickness,the NFR decreases with an increase in the skew angle.The decrease in NFR attributes to the rise in the plate's stiffness,increasing the plate's skewness on which the linear frequency rises.Meanwhile,the effect of porosity distributions on the NFR follows the trend as centrally distributed porosity (P) <evenly distributed porosity (P),irrespective of the skew angle,taper ratio,and various types of variable thickness.
Tables 11-13 demonstrate the influence of the thickness-tolength ratio of different types of variable thickness for various taper ratios and the plate's skewness on the NFR.The NFR decreases with an increase in the thickness-to-length ratio.This decrease is irrespective of the different types of variable thickness,taper ratio,skew angles,and porosity distributions.Such kind of behavior happens when the parameters are non-dimensionalized.It may be because of the rise in the plate's stiffness with an increase in thickness,and thus,the corresponding linear fundamental frequency increases.As expected,as the taper ratio increases,the NFR increases irrespective of thickness-to-length ratio,porosity distributions,and the skew angle.Analogously,for a given value of the thickness-to-length ratio,the influence of different types of variable thickness on NFR follows the trend observed in the previous examples,i.e.,exponentially variable thickness <linearly variable thickness <bi-linearly variable thickness.
The effects of aspect ratio on the NFR for different types of variable thickness,taper ratio,geometrical skewness are presented in Tables 14-16.These tables disclose that with an increase in the aspect ratio,the NFR decreases and then increases for lower skew angles (Φ=0and 15) and increases progressively for the higher skew angles say Φ=30and 45.This erratic change of the NFR for a higher aspect ratio is due to reduced actual inertia due to porosities and reduced stiffness.This kind of unexpected behavior appears due to the non-dimensionalizing of the parameters.An additional interesting observation is that for a given value of aspect ratio,the influence of different types of variable thickness on NFR follows the trend as linearly <bi-linearly <exponentially changing thickness.It may be due to degradation of material properties and increased porosities as the aspect ratio increases.Furthermore,the NFR is lowest in the centrally distributed porosities than evenly distributed porosities (P<P).
5.3.Parametric studies
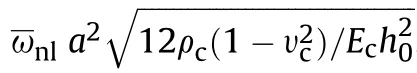
Fig.3 (a)-(f) depict the results for non-dimensional NFP of linearly TPFGS plate.The taper ratio taken for uniform thickness and non-uniform thickness (h/h) is 1 and 1.5,respectively,considering different boundary conditions for evenly distributed(P)and centrally distributed(P)porosities.Results show that for a given taper ratio and skew angle,the NFP obtained is maximum at the ideal tapered FGS plate (e=0);meanwhile,the NFP trend decreases with an increase in porosity parameter index(e)for the TPFGS plate.Thus,this signifies that ideal FGS plates are stiffer than the TPFGS plates.Besides,results reveal a rapid decrease in the NFP for the evenly distributed porosities (P) with an increase in the porosity parameter index(e).In contrast,the decrease rate is slow and steady for the centrally distributed porosities(P).The NFP can be assumed to be constant for the centrally distributed porosities(P)with an increase in the porosity parameter index(e).Thus,the NFP of Pis more harmful than the P.A further exciting comparison is that the NFP increases with an increase in the taper ratio(h/h)for a given skew angle.However,increasing NFP is seen with an increase in the TPFGS plate's geometrical skewness for a given taper ratio.Because the stiffness increases with an increase in the skew angle and taper ratio.Furthermore,Fig.3.(a)-(f)illustrate that the dimensionless NFP increases with an increase in the number of boundary edge constraints.However,the non-dimensional NFP for ideal tapered FGS plate(e=0)exhibits the higher side compared to TPFGS plate for all boundary conditions.Thus,the order of increasing the dimensionless NFP with boundary constraints is SSSS <SCSC <CCCC.The increase in the NFP from SSSS to CCCC is an average of almost 30%.This attributes to the fact that the flexural rigidity increases with an increase in boundary constraints.
Fig.4 (a)-(f) and 5 (a)-(f) depict the results for nondimensional NFP of both bi-linearly and exponentially variable thickness of the TPFGS plate with different boundary conditions for evenly distributed(P)and centrally distributed(P)porosities.The taper ratio for uniform and non-uniform thickness for bi-linearly(h/h) and exponentially (h/h) variable thickness is 1 and 1.5,respectively.The figures show that a similar kind of trend is observed for both bi-linearly and exponentially variable thickness,as presented in linearly variable thickness.In addition,for a given value of skew angle and taper ratio,the effects of different types of varying thickness on the NFP follows a trend as exponentially <linearly <bi-linearly variable thickness and exhibits the highest NFP in the centrally distributed porosities compared to evenly distributed porosities (P<P) for all the boundary conditions considered.It can also be noticed that the NFP of the TPFGS plate is always more significant than the uniform PFGS plate.
6.Conclusions
The present study uses the nonlinear FE formulation in the framework of FSDT in colligation with von Karman's assumptions to investigate the influence of porosity distributions on the nonlinear free vibrations of a tapered porous functionally graded plate with the consideration of geometrical skewness and various types of variable thickness.The equations of motion are derived using Hamilton's principle.The useful material properties of the TPFGS plate are predicted using the modified power-law distribution and Voigt's model.The nonlinear frequency results are computed through the direct iterative method.Validations and comparison studies have been carried out to check the proposed model's reliability.Following are the concluded outcomes from the present study.
1.In the presence of porosities,the NFR(ω/ω)decreases initially and then increases with an increase in the volume fraction index(m) for all the types of variable thickness,taper ratio,skew angles,and porosity distributions.
2.The NFR increases with an increase in the taper ratio and amplitude ratio.However,it decreases for the rise in the plate's skewness and porosity parameter index,irrespective of various types of variable thickness and porosity distributions.
3.The effect of bi-linearly variable thickness is high compared to linearly variable and exponentially variable thickness on both NFR and NFP.It follows the trend as exponentially variable thickness <linearly variable thickness <bi-linearly variable thickness.Hence,exponentially and linearly varying thicknesses can be considered for the thickness optimizations of TPFGS plates.
4.The geometrical non-uniformities on the PFG plate are always more significant than the PFG plate with uniform thickness for both NFR and NFP cases.
5.The NFP of the centrally distributed porosity (P) decreases steadily for all boundary conditions and various types of variable thickness with an increase in porosity parameter index.In contrast,the NFP of the evenly distributed porosities decreases rapidly.Hence,the NFR and NFP are more susceptible to the centrally distributed porosity than evenly distributed porosity.The influence of porosity distributions on the NFR follows the trend as P<Pand for the NFP,the tendency is P>P.
6.The NFP follows the sequence of increasing order with boundary conditions as SSSS >SCSC >CCCC.The average of almost 30%is the increase in the NFP from SSSS to CCCC.
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
The generalized nodal strain displacement matrices
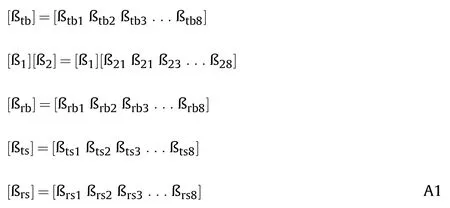
Whereas,[ß],[ß],[ß],[ß],[ß]and[ß](n=1,2,3,…,8)are the sub-matrices and are given by



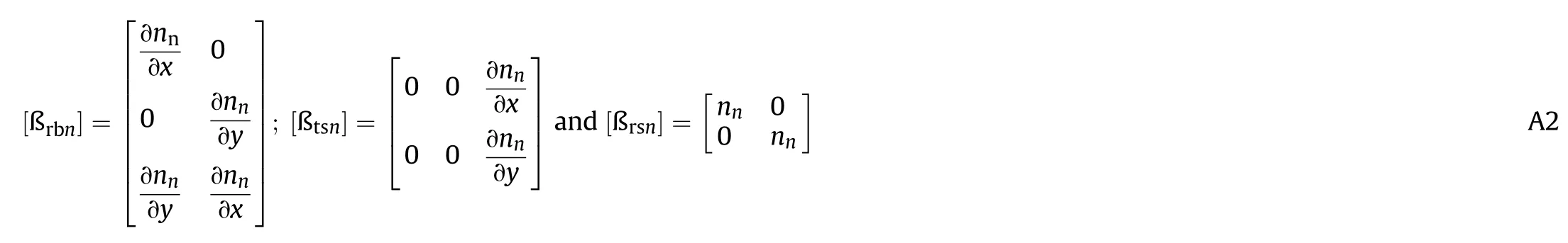
From Eq.(28),elemental stiffness matrices which correspond to bending and stretching
deformations and transverse shear deformations are given by


The various rigidity vectors and the rigidity matrices are given by
杂志排行
Defence Technology的其它文章
- Effect of porosity on active damping of geometrically nonlinear vibrations of a functionally graded magneto-electro-elastic plate
- Theoretical predict structure and property of the novel CL-20/2,4-DNI cocrystal by systematic search approach
- Manipulator-based autonomous inspections at road checkpoints:Application of faster YOLO for detecting large objects
- Penetration and internal blast behavior of reactive liner enhanced shaped charge against concrete space
- Failure investigation on high velocity impact deformation of boron carbide(B4C)reinforced fiber metal laminates of titanium/glass fiber reinforced polymer
- Compressive sampling and reconstruction in shift-invariant spaces associated with the fractional Gabor transform
