Compressive sampling and reconstruction in shift-invariant spaces associated with the fractional Gabor transform
2022-06-27QiangWangChenMengChengWang
Qiang Wang,Chen Meng,Cheng Wang
Shijiazhuang Campus,Army Engineering University,Shijiazhuang,PR China
Keywords:Compressive sampling Reconstruction Shift-invariant space Fractional gabor transform Chirp-like signals
ABSTRACT In this paper,we propose a compressive sampling and reconstruction system based on the shift-invariant space associated with the fractional Gabor transform.With this system,we aim to achieve the sub-Nyquist sampling and accurate reconstruction for chirp-like signals containing time-varying characteristics.Under the proposed scheme,we introduce the fractional Gabor transform to make a stable expansion for signals in the joint time-fractional-frequency domain.Then the compressive sampling and reconstruction system is constructed under the compressive sensing and shift-invariant space theory.We establish the reconstruction model and propose a block multiple response extension of sparse Bayesian learning algorithm to improve the reconstruction effect.The reconstruction error for the proposed system is analyzed.We show that,with considerations of noises and mismatches,the total error is bounded.The effectiveness of the proposed system is verified by numerical experiments.It is shown that our proposed system outperforms the other systems state-of-the-art.
1.Introduction
As the cornerstone of digital signal processing,Nyquist sampling theorem states that,to perfectly reconstruct band-limited analog signals,the sampling rate must be at least twice the highest frequency of signals [1,2].Although the band-limited assumption is often approximately met,many signals in applications may not be adequately modeled in frequency domain.Over the past two decades,substantial progress has been made in the sampling theories.That results in some new and reliably sampling methods accommodating more general signals [3-6].
Shift-invariant (SI) space theory is such a powerful tool for a large family of signals.It allows perfect recovery of signals from its linear or nonlinear samples under very broad conditions [7,8].Typically,the SI space with M generators can be defined by

where a(t) is the generator for space V .
The SI space allows perfect recovery of signals from M sample sequences obtained by filtering input signals with a bank of M filters.The output in each filter is uniformly sampled at the rate of 1/T,such that the overall sampling rate is M/T.Under this conception,the well-known Nyquist sampling theorem,whose generator is a single sinc function,can be viewed as a special case of SI space sampling theory [6].
Recently,the sampling theory in SI space has been extended to the more general situations.For example,in Ref.[9],the shiftinvariant subspace in mixed Lebesgue space is defined,and the fast reconstruction algorithm allows exact reconstruction of signals from the non-uniform samples.In Ref.[10],a continuously differentiable function satisfying certain decay conditions is introduced to generate the SI space,such that the unique and stable reconstruction can be achieved from the local averages on some discrete sets.In Ref.[4],the conception of SI space is extended to the fractional Fourier transform (FRFT) domain,and the simplified nonideal sampling scheme associated with FRFT is proposed in Ref.[7] to simplify the structure of sampling system in non-ideal cases.Some similar works can also be seen in Refs.[11-13].
Typically,M generators in SI space requiring M sampling sequences for reconstruction will,as expected,result in M sampling channels.To reduce the channel number,the works[6,14]design a novel sub-Nyquist sampling system based on the compressive sensing (CS) theory.Under this scheme,the channel number of sampling system can be reduced to P(2K=P ≤M),when only K out of M generators are active for generating the signals.These works provide a novel scheme to implement the compressive sampling for analog signals.However,before bringing this scheme into practice,some specific issues still require further study,such issues as the appropriate construction of SI space,efficient and feasible implementation for filters,and accurate reconstruction for input signals.
Actually,CS theory has aroused great interest in sampling theory over the recent two decades,and fruitful results have been made in the construction of feasible compressive sampling system.Random Demodulator (RD) is a typical CS-based compressive sampling system achieving sub-Nyquist sampling for analog signals [15,16].However,this scheme is only suitable for specific signal classes,such as the signals consisting of finite set of harmonic components.Modulated Wideband Converter(MWC)[17]is another mature CSbased compressive sampling system.It is designed for the sub-Nyquist sampling of multiband signals,making it well suited to cognitive radar [18,19].However,when the spectral content of signals resides within a wide spectrum range,MWC is incapable to capture sufficient information to reconstruct the input signals accurately.Recently,some modifications have been made for the conventional CS-based compressive sampling systems.In Ref.[20],the conventional RD is extended to a generalized structure,such that chirp-like signals can be well reconstructed after the sub-Nyquist sampling.In Ref.[21],the windowed MWC is presented to acquire chirp-like signals without the prior information of carrier frequency and chirp rate.In Refs.[22,23],a generalized multichannel compressive sampling system based on MWC is proposed by exploring the sparsity of chirp-like signals in fractional Fourier domain.
The chirp-like signals are widely used in many fields,such as radar,sonar,or communication systems [24-26].Due to the increasingly complicated applications,the chirp-like signals are expected to work at wide bands to cope with new challenges[27].Compressive sampling system has the potential to acquire signals well-below the Nyquist rate,which may lead to significant reduction in the sampling costs,power consumption,and hardware requirement.As a consequence,compressive sampling system is viewed as a panacea for wideband signals to achieve the efficient sampling[28,29].Nowadays,the compressive sampling systems for chirp-like signals are mainly based on the FRFT [20,22,23].However,FRFT integrates the signals over all time to obtain the fractional-frequency components in general.In words,the fractional-frequency spectrum loses the time-varying information.As is well known,some chirp-like signals observed in the real world are time-varying,which often requires signal analysis tools to capture the time-varying characteristics of signals [30].
In this paper,the compressive sampling and reconstruction for the time-varying chirp-like signals is considered.Our work is motivated by the CS-based SI space sampling theory and a novel short-time FRFT (STFRFT).Our main contribution is a compressive sampling and reconstruction system achieving the sub-Nyquist sampling and accurate reconstruction for time-varying chirp-like signals.
Under the proposed scheme,the time-varying chirp-like signals are stably expanded on the SI space associated with fractional Gabor transform(FRGT),which has the ability to analyze the signals in the joint time-fractional-frequency domain.We introduce the conception of FRGT based on a novel STFRFT proposed in Ref.[30].Under the frame theory,we analyze the completeness of signal expansion,and then provide the biorthogonality of FRGT.Utilizing the inherent sparsity of signals in the joint time-fractionalfrequency domain,the CS theory is introduced to achieve the sub-Nyquist sampling.We present the compressive sampling and reconstruction system,and then establish the sampling and reconstruction models for it.In reconstruction,a block multiple response extension of sparse Bayesian learning algorithm is proposed to guarantee the accurate reconstruction for time-varying chirp-like signals.In addition,the reconstruction error is proven to be bounded with considerations of noises and mismatches.Finally,the effectiveness of the proposed scheme is verified by some numerical experiments.
The remainder of this paper is organized as follows.In Section 2,we introduce the problem formulation based on some basic preliminaries.In Section 3,the SI space is defined by introducing the conception of FRGT.In Section 4,CS theory is implemented into the SI space to achieve the sub-Nyquist sampling and accurate reconstruction.In Section 5,numerical experiments are conducted to evaluate the effectiveness of the proposed scheme.
2.Preliminaries
2.1.Notation
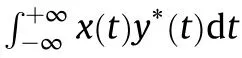
2.2.Sampling in SI space
SI space sampling theory deals with problem of recovering the signals from its uniform samples.With this scheme,the sampling and recovery are conducted by filtering operations.For signal x(t)∈V,the sampling and reconstruction in SI space [6] can be depicted in Fig.1.
With the expression of(1),the Fourier transform for signal x(t)is given by

where A(ω)is the Fourier transform for a(t),D(e)is the discretetime Fourier transform for d[k].The filter output is discretized in time to obtain the samples c[k],to yield

The relationship between coefficients d[k] and samples c[k] is given by

where c(e),d(e)and M(e)are denoted by
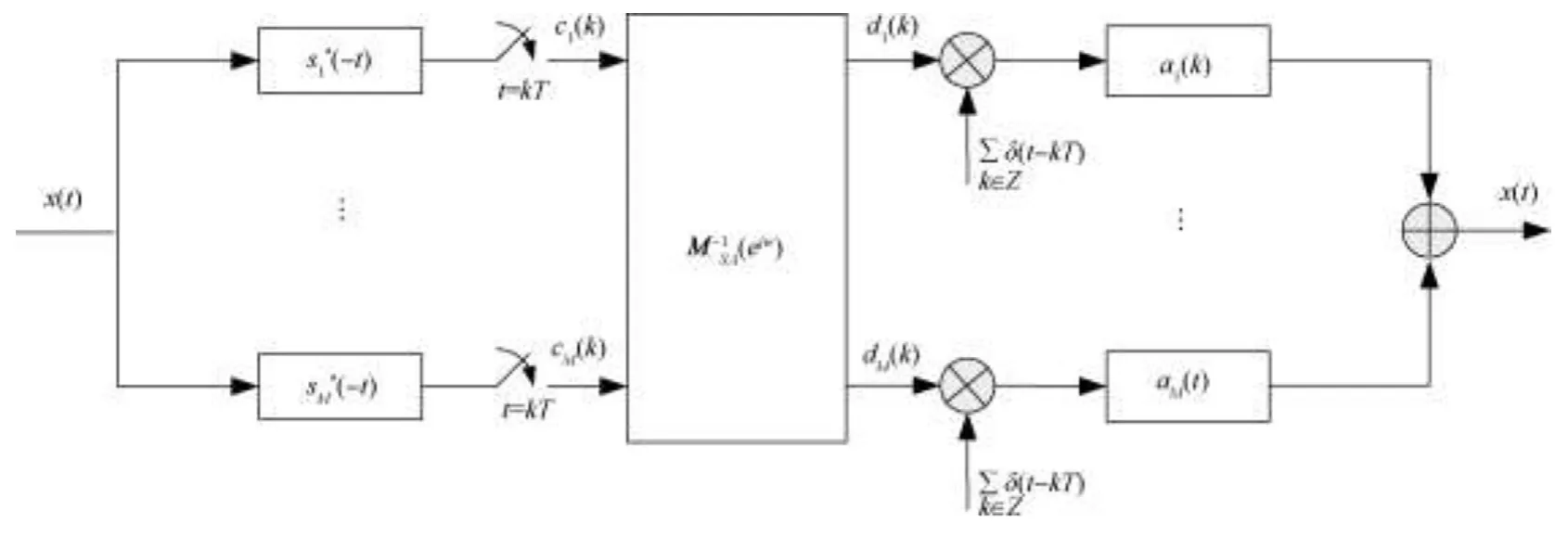
Fig.1.Sampling and reconstruction in SI space.
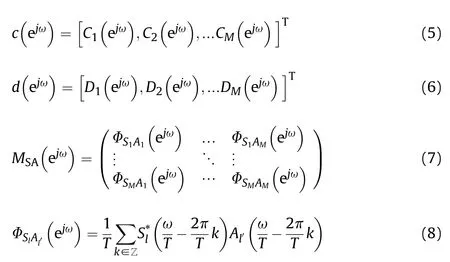
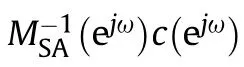
2.3.Compressive sampling in SI space
The sampling method depicted in Fig.1 is achieved by M sampling channels,each at rate 1/T,resulting in an overall sampling rate M/T.In principle,if the signals are generated by K out of M generators,as long as the chosen subsets are known,it suffices to sample signals at an overall rate of K/T corresponding to uniform samples with period T at the output of K filters.However,in the more general situation,we may not know the exact subspace in which the signal resides.To deal with it,in Ref.[14],a sub-Nyquist sampling and reconstruction method based on SI space and CS theory is proposed.This scheme is presented in Fig.2.Here,the input signals are processed by P filters,at the rate 1/T,leading to a system with overall sampling rate P/T,where 2K=P ≤M is determined by the requirements of standard CS theory.
In frequency domain,the filter is given by:

where A is the measurement matrix under CS theory,W(e)is an arbitrary P × P invertible matrix with element W(e),s(ω)and v(ω)are vectors whose lth elements are S(ω)and V(ω)respectively.V(ω)is the Fourier transform for v(t),and the function v(t) is biorthogonal to a(t),satisfying
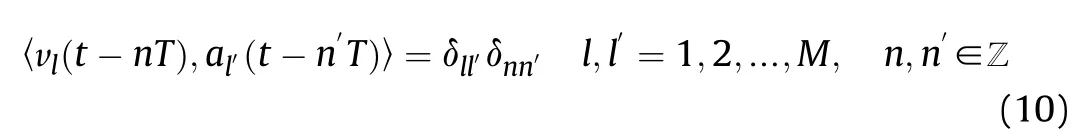
In time domain,the filter s(t),1=p ≤P,can be further depicted as

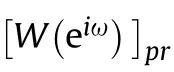
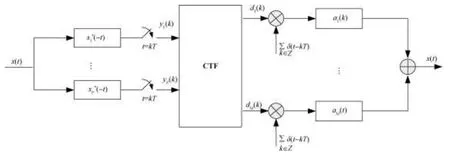
Fig.2.Compressive sampling and reconstruction in SI space.

and Y(e)is the discrete-time Fourier transform for y[n].Besides,the reconstruction model in (12) is typically an infinite measurement vector (IMV) problem.To solve it,the continuous-to-finite(CTF) block is used to convert the IMV problem into a multiplemeasurement vector (MMV) problem [31].
The scheme in Fig.2 provides a feasible sub-Nyquist sampling and reconstruction method in SI space.To bring this scheme into practice;some specific issues still require further study.Firstly,the effective reconstruction for input signals depends on the sparsity of coefficients d[k].In words,it is important to construct an appropriate SI space to make sure that the signals are sparsely expanded.Secondly,a feasible simplification for the sampling system is needed since the filter depicted in (11) is too complex to be implemented in hardware circuit.Thirdly,given the SI space,it is meaningful to explore the effective algorithm to improve the reconstruction performance.
3.The SI space associated with FRGT
3.1.The conception of FRGT
In this paper,we consider the sub-Nyquist sampling and reconstruction for chirp-like signals with time-varying properties in SI space.To make sure that the sub-Nyquist sampling process can gain sufficient information,appropriate generators for SI space are studies based on FRGT.
The FRGT studied in this paper is a class of STFRFT that employs discrete lattices in the joint time-fractional-frequency plane.Presently,there are several schemes to implement the STFRFT for signals [32-35].Particularly,in the work [30],a novel STFRFT is presented to analyze the time-varying fractional-frequency content for signals in terms of the FRFT-domain filter bank.
For signal x(t)∈L(ℂ),the STFRFT can be expressed as:
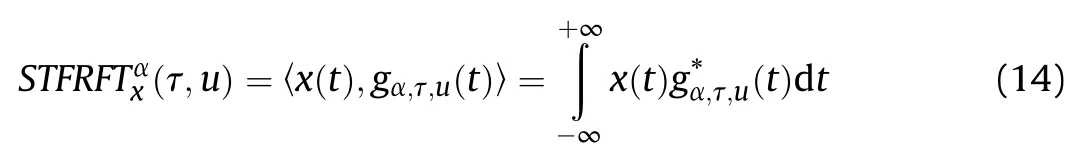
where α is the fractional angle,and the kernel follows that

Given the window function γ(t)satisfying

the inverse STFRFT can be expressed as

As mentioned in Ref.[30],the time-fractional-frequency coefficients of STFRFT can be obtained by a filter bank,which makes it suitable for sampling system designing.However,the continuous time-fractional-frequency lattices hinder the further reduction in the sampling rate.Therefore,to achieve the sub-Nyquist sampling for signals,we propose the FRGT based on the STFRFT mentioned above.
For signal x(t)∈L(ℂ),the FRGT proposed in this paper is given by
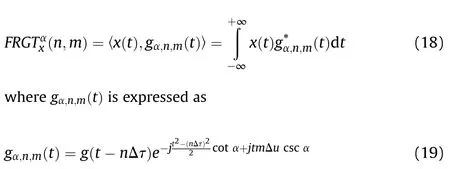
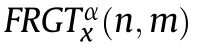
The collection

for all x(t)∈L(ℂ).The constants A,Aare frame bounds,and the frame is called tight,if A=A.


The collection
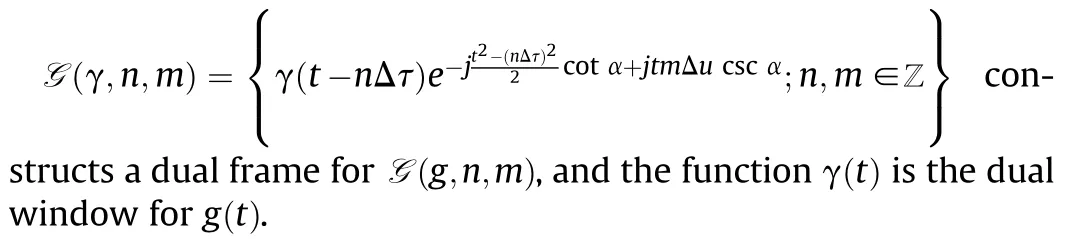
According to the sampling density (which is also the lattice density)defined by d=(ΔτΔucsc(α)/(2π)),the characterization of collection G(g,n,m)can be divided into three categories:
a) Undersampling-d<1;
b) Critical sampling-d=1;
c) Oversampling-d>1.
In the case of undersampling,the expansion for signals is incomplete,such that it is impossible to construct a frame.The necessary condition for a frame is d ≥1,whereas critical sampling occurs when d=1.And once the frame is formed,the expansion for signal will be complete and any signals in L(ℂ)can be recovered by formular (21).
3.2.Biorthogonality of FRGT
The frame theory establishes the completeness of signal expansion.However,the calculation for frame bounds and dual window suffers from high computing complexity.To cope with it,the biorthogonality of FRGT is studied.
Assume that the signal x(t)∈L(ℂ)can be represented by Eq.(21).Then substituting (18) into (21) yields the following completeness condition as

where δ(t)is the delta function.
In the following content,we will prove that the completeness condition in (22) is equal to the biorthogonality between γ(t)and g(t).
The completeness condition can be further expressed as

Assume that
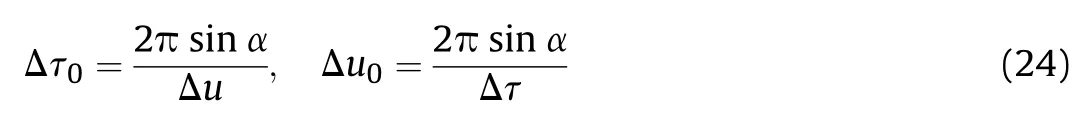
then according to the Poisson sum formula,we have
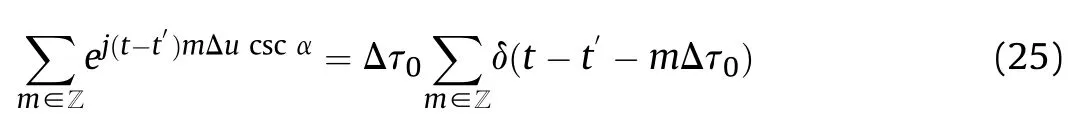
Substituting (25) into (23) yields
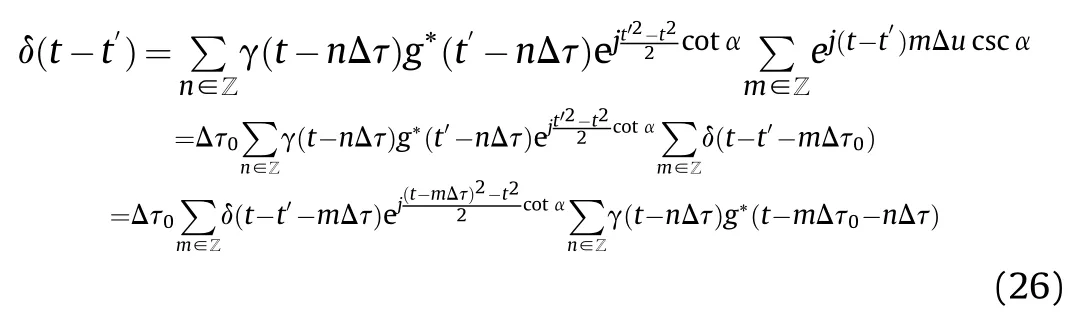
Using the Poisson sum formula again,we have
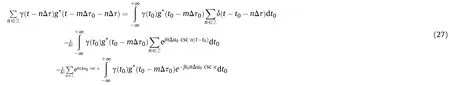
Substituting (27) into (26) yields
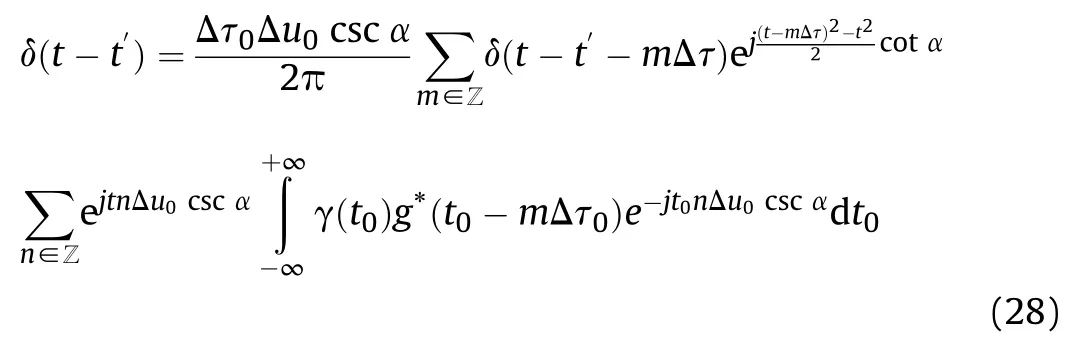
Thus,Eq.(28) holds if and only if
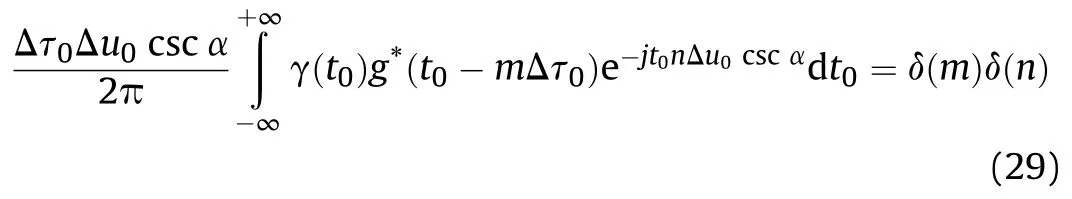
which is the biorthogonality of FRGT.
Given the function g(t),dual window γ(t)can be calculated by the biorthogonality in(29).The existence of dual window requires that ΔτΔucsc(α)≤2π,which conforms to the results in frame theory.
3.3.Filter designing in SI space
It is indicated in the expression of(21)that the fractional Gabor expansion is a special case of SI space with the generators related to each other in a simple way.Therefore,the SI space associated with FRGT can be depicted as

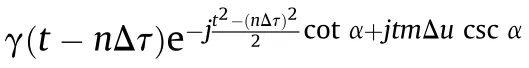

We define the fractional convolution operator*as

where*denotes the conventional convolution operator.Within the FRFT domain,fractional convolution corresponds to multiplication as

Here,G(u csc α)is the Fourier transform for g(t) scaled by cscα,K(t,u)is the kernel for FRFT defined by
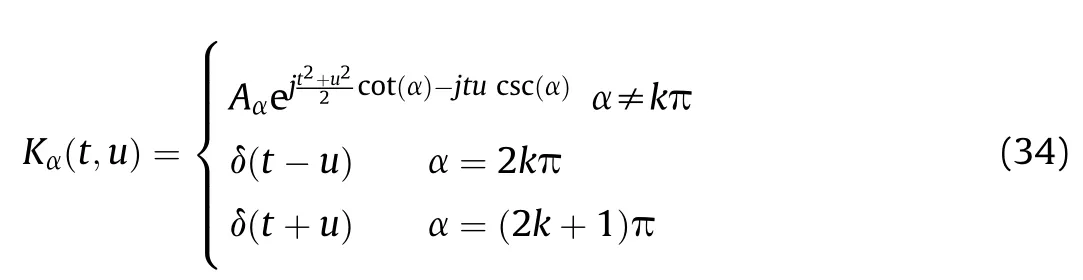
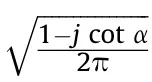

Then Eq.(31) can be rearranged as
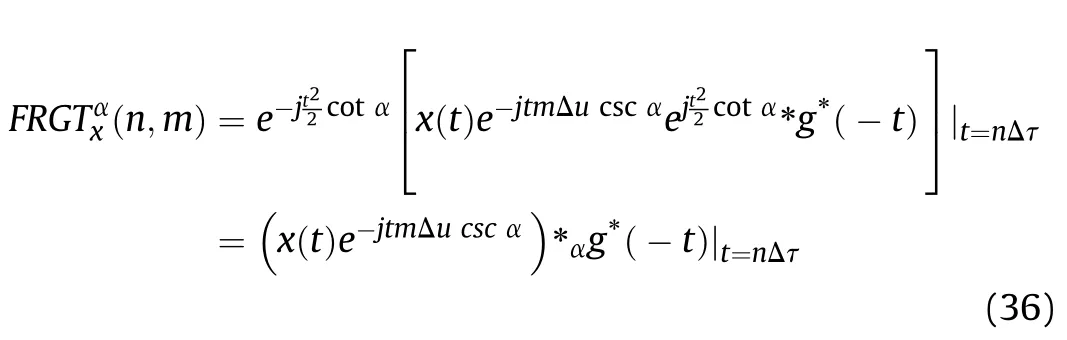
Correspondingly,in FRFT domain,we have
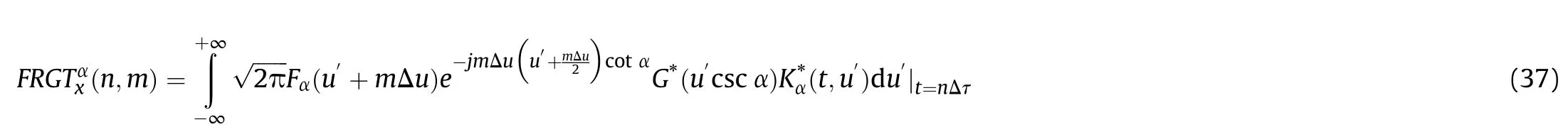

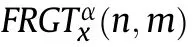

4.Compressive sensing in SI space associated with FRGT
4.1.Expansion with finite coefficients in SI space

Fig.3.Filter designing to obtain .
It is implied in Eqs.(36)and(37)that the sampling for signals in SI space associated with FRGT can be implemented in a filter bank.However,as depicted in(30),the infinite generators mean a bank of infinite filters,which is obviously impossible to be implemented in practice.Besides,the infinite samples in one filter also lead to IMV model during the compressive sampling and reconstruction.To deal with this problem,appropriate assumption is adopted for the chirp-like signals to simplify the sampling and reconstruction process.
Typically,the chirp-like signals used in practice are compactly supported in time.For example,in the radar system,the transmitted signals are usually periodic chirp pulses.In one period,the transmitter firstly works to transmit one chirp pulse.Then,the receiver works to sample the echoes[38].The intermittent working mode makes both the transmitted signals and echoes compactly supported within one period.
To sample the transmitted signals or echoes in one period,we assume that x(t)is compactly supported on the interval [0,T].Moreover,since the signals typically reside within a limited band in fractional-frequency domain,we assume that x(t)is essentially ε-bandlimited in [-Ω/2,Ω/2],to yield

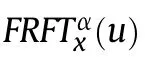
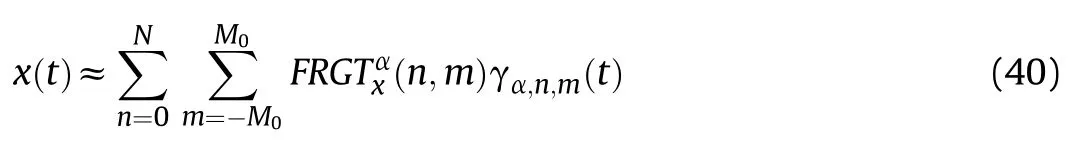
where

It is implied that only 2M+1 filters with N+1 samples in each filter are needed to make an approximate expansion for signal x(t)in the SI space associated with FRGT.
4.2.System designing
Typically,time-varying chirp-like signals show a good sparsity in FRGT.For further illustration,an example is shown in Fig.4.The expression of signal is given by
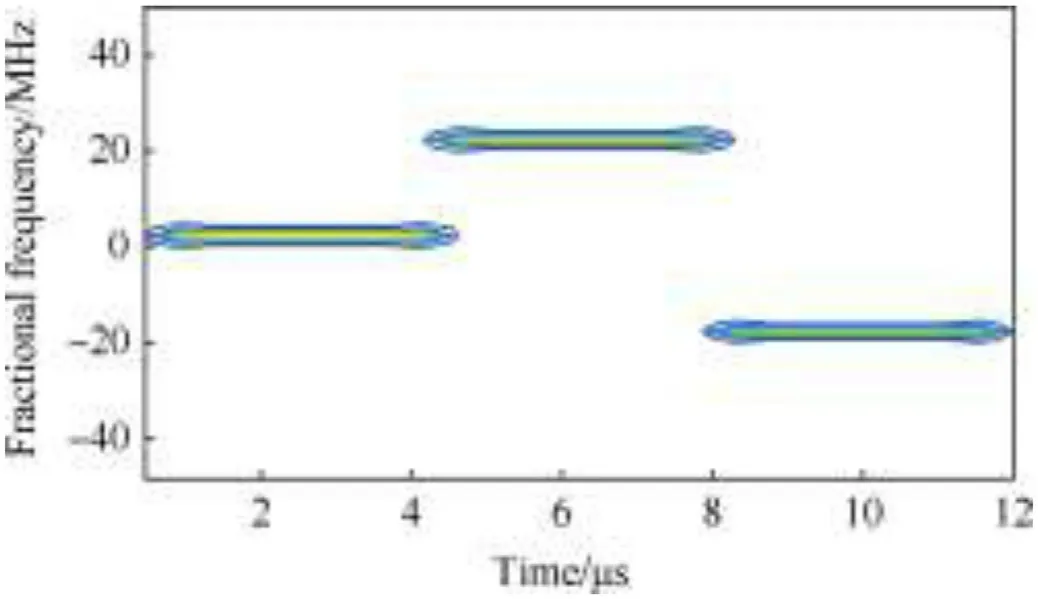
Fig.4.FRGT for signals given in (42).

where chirp rate k’=3×10Hz/μs.
It is seen that the time-varying properties bring the signals an inherent sparsity in the joint time-fractional-frequency domain.That gives us the inspiration to design a compressive sampling and reconstruction system in the SI space associated with FRGT.
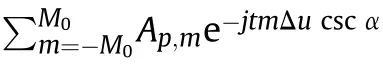

where M=2M+1.
Here,two conjugate chirp components are used to construct the FRFT-domain low-pass filter.The filter output is sampled at the rate 1/Δτ,and then the overall sampling rate is P/Δτ.As 2K=P ≤M,it is indicated that compared with the direct sampling in SI space,the proposed compressive sampling system reduces the channel number of sampling system.Due to the existence of low-pass filter,the sampling rate in one channel can be much lower than Nyquist rate.In addition,with an appropriate value of P,the overall sampling rate of proposed sampling system can also be lower that Nyquist rate.
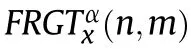

4.3.Sampling and reconstruction models analysis


Fig.5.The proposed compressive sampling and reconstruction system.

Assume that

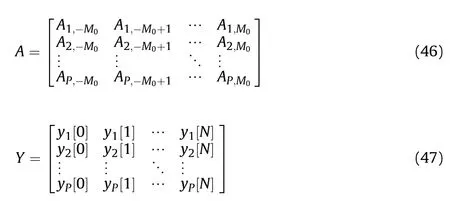
where G∈ℂis the coefficient matrix,A∈ℝis the measurement matrix,Y∈ℂis the filter output matrix.The relationship between filter outputs and coefficients can be rewritten as

With the expression in (48),we aim to reconstruct the coefficient matrix G from the filter output matrix Y.Since P <M,the reconstruction problem is ill-conditioned.However,it can still be solved by optimization algorithms when the columns in G show good sparsity.
Under the theory of CS,the successful reconstruction for sparse matrix G requires the measurement matrix A to satisfy the Restricted Isometry Property (RIP) [39].From the expression of(43),we can find that measurement matrix used in the proposed system is a kind of random measurement matrix,which is named as Bernoulli random matrix.The RIP of Bernoulli random matrix has been studied in some previous works[40,41].The main results are presented in Lemma I.
Let A be a random P×M matrix whose entries Aare drawn according to the distribution in (43).Given M,K,δ∈(0,1)and P≥O(K×log(M/K)),there exist constants c,c>0 depending on the δand A satisfying 3K-order RIP with probability

where
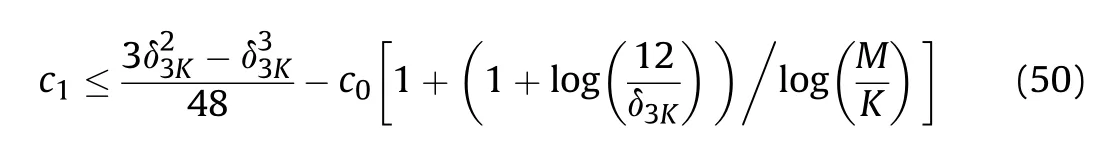
To simplify matters,it is useful to introduce the notation

where I [·] denotes the indicator function,‖·‖ is an arbitrary vector norm,Gis the (m+M+1)th row of G.In essence,d(·)measures the row-diversity as it counts the number of rows in a matrix that are not equal to zero.With the measurement matrix A satisfying RIP,the reconstruction model for coefficient matrix G can be expressed as
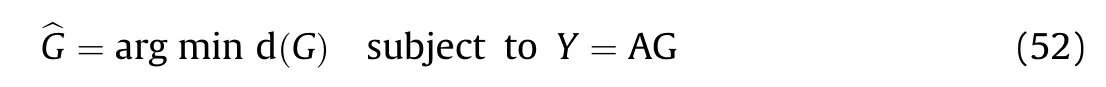
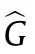
4.4.Reconstruction algorithm
Due to the inherent sparsity of chirp-like signals in the joint time-fractional-frequency domain,the reconstruction model presented in (52) is typically an optimization problem with multiple sparse vectors.Nowadays,many algorithms,including Simultaneous Orthogonal Matching Pursuit (SOMP) [42],Multiple Signal Classification (MUSIC) [43],and Multiple Response Extension of Sparse Bayesian Learning (M-SBL) [44],have been proposed to solve this problem.Compared with other algorithms,M-SBL provides the better estimation for sparse coefficients at the existence of noises,and can utilize the correlation between different vectors to enhance sparse optimization solutions.That inspires us to introduce the M-SBL to solve the reconstruction model in this paper.
Under the scheme of M-SBL,measurement noise is considered in the sampling model as

where N is the noise matrix.For 0=n ≤N,we assume that Yis the(n+1)th column for Y.Similarly,Gis the(n+1)th column for G,Nis the (n+1)th column for N.Then we have

Assume that Nis the zero-mean Gaussian noise with the variance σ.Then the distribution of Ycan be expressed as

Next,we assign a M-dimensional Gaussian prior to G(the(m+M+1)th row of G),to yield

where ξis an unknown variance parameter.By combining each of these row priors,we arrive at a full coefficient prior

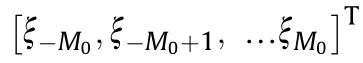

with the mean and covariance given by

where Γ=diag(ξ),Σ=σI+AΓA.The parameter σ and hyperparameter vector ξ can be estimated by maximizing a marginal likelihood,which is given by

For detail deduction,please refer to the work[44].Here we give the parameter estimation results as

As given in (56),entries in the row are drawn from the same distribution.In words,the good performance of M-SBL requires different columns in G having high correlation.It is seen from(45)that the column Gis actually the fractional-frequency coefficients at the time nΔτ.Therefore,for the time-varying chirp-like signals considered in this paper,the high correlation amount all columns of G is unsatisfied.However,within a short time interval,the signal property may stay the same,such that the high correlation for corresponding columns will be possessed.One example is shown in Fig.4.It is seen that the adjacent columns within a short time interval(for example 0=t <4)have similar appearance in fractional frequency.
Utilizing this property,a novel block M-SBL(BM-SBL)algorithm is proposed to improve the reconstruction performance.With the proposed algorithm,the filter output matrix Y is firstly divided into several blocks,and each block contains several adjacent columns of Y.Then the conventional M-SBL algorithm is conducted for each block to reconstruct corresponding coefficients.Assume that the block number is Q,then each block contains(N+1)/Q columns.For 1=q ≤Q,the qth block Yis given by

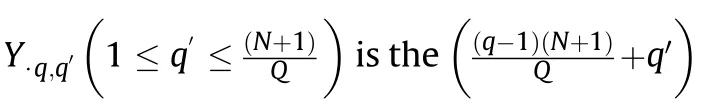
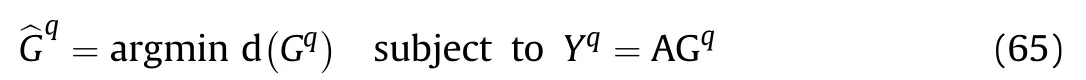
Similar to (64),coefficient block Gis given by

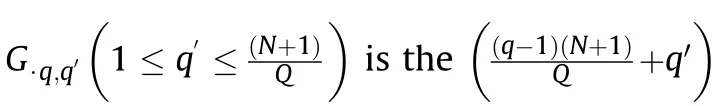
4.5.Reconstruction error analysis
With the coefficient matrix,it is depicted in Fig.5 that the original signals can be recovered from the time-fractionalfrequency coefficients.However,in practice,the sampling and reconstruction system will inevitably be interfered by noises and mismatches.More specifically,the sampled signals may contain noises and the sampling process may be interfered by some uncertain factors such as circuit crosstalk,grounding and measurement instability.On the other hand,there are also mismatches for the whole system,such as the approximation in signal expansion and non-ideal filter functions.Considering the noises and mismatches,in this sub-section,we make an analysis for the reconstruction error.
We assume that the sampled signals consist of two components as

where x(t)is the true signal without noises,e(t)is the Gaussian noise.Then in the p-th channel,the filter output at time nΔτ can be given by

Besides,we introduce w[n]as the Gaussian noise generated by sampling process.Then the filter output can be rewritten as
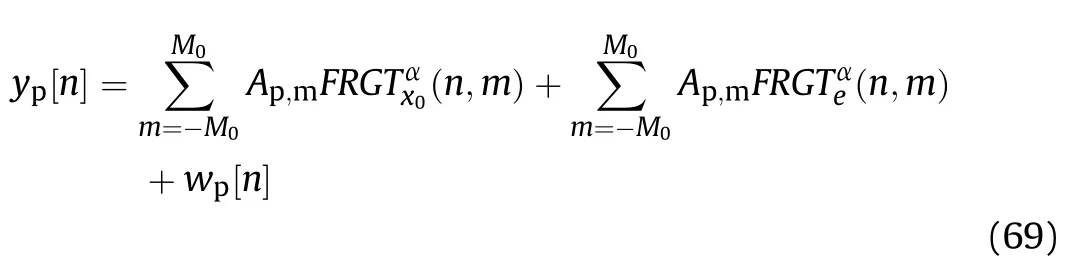
In matrix form,we have

where Gand Gare coefficient matrices constructed by x(t) and e(t) respectively,and W is the noise matrix with entries w[n].Assume that N=AG+W,then we have

which is consistent with the sampling model in (53).For further analysis,the matrix N is assumed to be bounded as‖N‖≤ε,such that the reconstruction model is rewritten as
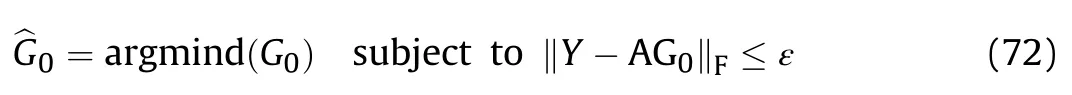
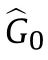
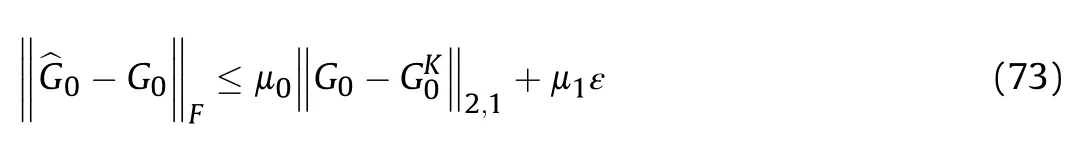

As analyzed in sub-Section 4.1,the finite sampling channels actually make an approximation for signals within the essential fractional-band F=[-Ω/2,Ω/2].To measure the approximation error,we assume that

Then according to the expression of (39),we have
In words


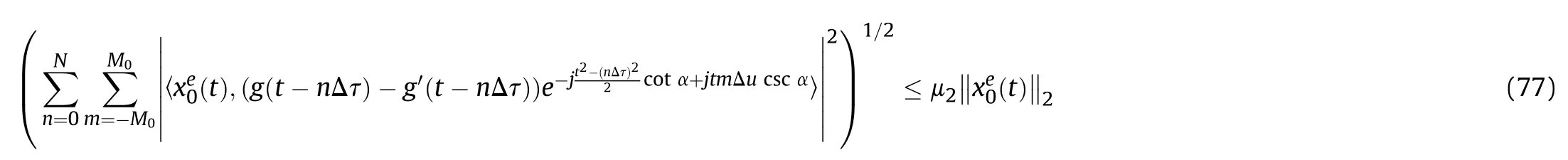
Then we have
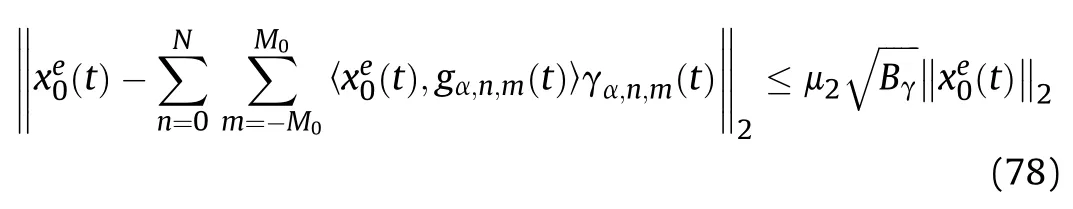
where Bis the upper bound for the frame constructed by γ(t).
Proof:See Appendix A.
Considering both the noises and mismatches mentioned above,we now present a total reconsruction error in Corollary I.

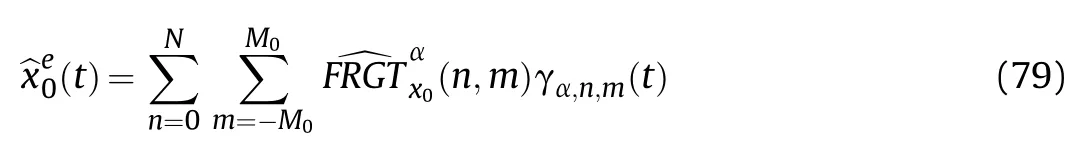
with the total error
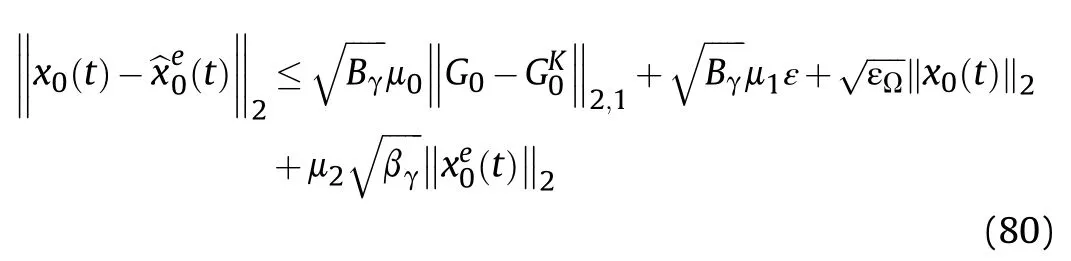
Proof:See Appendix B.
It is seen in (80) that with considerations of noises and mismatches,the total error is bounded.
5.Numerical experiments
We now present some numerical experiments to illustrate the effectiveness of the proposed compressive sampling and reconstruction system.We test the time-varying chirp-like signal x(t)given by (42),which is composed of finite-duration chirps of the same chirp rate and different center frequencies.The signals are compactly supported on the time interval [0,12 μs],and correspondingly,the essential fractional-band is limited to [-50 MHz,50 MHz].Indicated by (38),Gaussian function is used to generate the window g(t) with the widths T=1.5 μs,Ω=6 MHz.

Fig.6.The analysis for sampling density:(a) (D-C)/C with different Δucsc(α)/2π,(b) RE with Δτ varying from 0.1 μs to 1 μs.
5.1.Analysis for sampling density
The proposed compressive sampling and reconstruction system requires an appropriate Δτ and Δu to make sure that the original signals can be completely recovered from the time-fractionalfrequency coefficients.To construct a frame,a necessary condition requires that
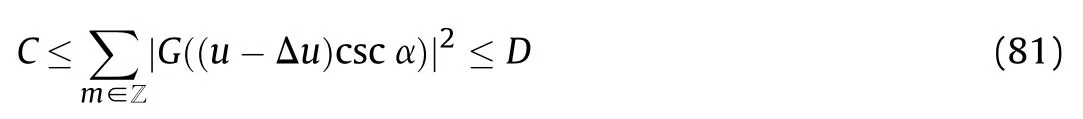

Fig.7.Reconstruction probability with different channel number:(a) Δτ=0.4 μs,(b)Δτ=0.5 μs,(c) Δτ=0.6 μs
where 0<C≤D<∞,G(u csc α)is the Fourier transform for g(t)scaled by cscα.To make a robust reconstruction for original signals,C and D are supposed to be close.To measure the gap between C and D,we show the value(D-C)/C in Fig.6(a).For convenience,the horizontal axis is given by Δucsc(α)/(2π).It is seen that C and D get close with the decrease of Δucsc(α)/(2π).However,considering the implementation of sampling system,the small Δucsc(α)/(2π) will also lead to a large number of channels.Thus,we choose Δucsc(α)/(2π)=1.54 MHz to keep a small (D-C)/C and reduce the sampling channels as much as possible.
Another necessary condition for the completeness is d ≥1,whereas d=(ΔτΔucsc(α)/(2π)).Meanwhile,the value of Δτ will directly determine the number of samples in one channel,such that we want Δτ to be large to reduce the sample number.Since Δucsc(α)/(2π)=1.54 MHz,we have Δτ ≤0.65 μs To show the influence of Δτ,we set Δτ varying from 0.1 μs to 1 μs(0.1 μs <0.65 μs <1 μs),and then recover the signal x(t)from timefractional-frequency coefficients determined by Δτ and Δu.The coefficient number is indicated by(41),whereas T=1.5 μs,Ω=6 MHz.In addition,we measure the error by Relative Error (RE)

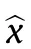
The completeness requires that Δτ ≤0.65 μs That is why when Δτ >0.65 μs,RE is large in Fig.6(b).When Δτ ≤0.65 μs,it is seen that RE reduces gradually with the decrease of Δτ.That means lower Δτ will contribute to the better representation effect for signals.However,as indicated by (41),lower Δτ will also lead to more samples.Therefore,in the following experiments,we set 0.4 μs ≤Δτ ≤0.6 μs to make a trade-off between sample number and RE.
5.2.Comparison for compressive sampling and reconstruction
After compressive sampling,we firstly use the compressive samples to reconstruct the time-fractional-frequency coefficients,and then recover the original signals under the SI space.The key step is the reconstruction for time-fractional-frequency coefficients,since we need to solve an ill-conditioned MMV problem.In this paper,the BM-SBL algorithm is proposed to improve the reconstruction effect.For comparison,some other algorithms are also introduced to conduct the reconstruction for time-fractionalfrequency coefficients including:
1) SOMP [42].
2) M-SBL [44].
3) Block Simultaneous Orthogonal Matching Pursuit (BSOMP)
4) BM-SBL
The BSOMP algorithm is an extension of SOMP.It shares the same blocks with BM-SBL,and for each block,conventional SOMP algorithm is conduct to reconstruct corresponding coefficients.According to the empirical value,we set block number Q=3,Δτ=0.4 μs,0.5 μs,0.6 μs respectively.For each Δτ,different sampling channels are used to sample the signals.For each setting,the Monte Carlo method is introduced to conduct the experiment 500 times.We calculate the RE between reconstructed coefficients and original coefficients.If RE <0.01,the reconstruction is viewed as success;otherwise,it is false.The reconstruction probability is shown in Fig.7.
From Fig.7,we can see that when channel number P is large enough,the time-fractional-frequency coefficients can be reconstructed with high probability.Besides,reconstruction algorithms also influence the reconstruction probability.By dividing the filter output matrix Y into several blocks,the correlation between columns in one block is strengthened,and corresponding row sparsity is lowered.Then BSOMP and BM-SBL achieve better reconstruction than SOMP and M-SBL.In general,BM-SBL achieves the better reconstruction than the others.Therefore,BM-SBL is more suitable to reconstruct the time-fractional-frequency coefficients.

Fig.8.Reconstruction probability with noises:(a) Δτ=0.4 μs,(b) Δτ=0.5 μs,(c)Δτ=0.6 μs.
Obviously,the input signals and sampling process will inevitably be mixed by noises.And as analyzed in(70),these noises will eventually be blended into the matrix Y.In this experiment,noises with different Signal-to-Noise Ratio (SNR) are added into the matrix Y.Then BM-SBL algorithm is used to reconstruct the timefractional-frequency coefficients.Based on the results in Fig.7,here the channel number is set as 26=P,such that in Fig.7 (a),Fig.7 (b) and Fig.7 (c),the reconstruction probability is always upper than 95%.In addition,we set Δτ=0.4 μs,0.5 μs or 0.6 μs,and SNR varies from 1 dB to 20 dB.Then the reconstruction probability is shown in Fig.8.
It is seen in Fig.8 that the reconstruction probability is directly impacted by SNR.When SNR is small,such as SNR≤11 dB,original signals will be submerged into the noises.Then it is hard to reconstruct the time-fractional-frequency coefficients effectively.With the increase of SNR,reconstruction probability is also increased.When SNR is large enough,such as SNR≥16 dB,high probability can be obtained.It is seen in Fig.8 that channel number P also affects the reconstruction probability.Typically,more channel number means more information about inout signals,resulting in a better reconstruction performance.However,the increase in channel number will also lead to the high overall sampling rate and sample number.Therefore,for practical applications,the value of P is supposed to be small as much as possible at the premise of high reconstruction probability.
For further comparison,different systems are considered to conduct the sampling and reconstruction for the chirp-like signals,including:
1) Traditional Nyquist sampling [1,2];
2) SI space sampling associated with FRGT;
3) SI space sampling associated with Gabor transform [45];
4) Generalized RD [20];
5) Generalized MWC [22];
6) Compressive sampling system in SI spase associated with Gabor transform [37];
7) The proposed system.
For convenience,we name these systems mentioned above as SYS I-VII.For SYS I,SYS II and SYS IIII,an perfect reconsruction is carried out under the SI space theory.Therefore,the reconstruction error is neglected.SYS IV-VII are compressive sampling systems,whereas SYS IV and SYS V are improved RD and MWC to achieve the sub-Nyquist sampling for chirp-like signals.SYS VI is a Gabor-based compressive sampling system proposed in Ref.[37] to reduce the sampling rate for short pulses.After compressive sampling,BM-SBL algorithm is used to reconstruct the sparse coefficients,and then the original signals are further recovered from corresponding sparse coefficients.For SYS IV,the reconstruction model is a SMV problem,such that BM-SBL algorithm changes into the SBL algorithm.In this experiment,we calculate the RE between reconstructed signals and original signals.The sampling numbers for SYS IV-VII are set to the same value.Then the sampling and reconstruction performances for different systems are summarized in Table 1.When considering the noises,we set SNR=16 dB.
For SYS II and SYS III,it is seen that the sampling rate (one channel) is reduced.However,the overall sampling rate is still larger than SYS I.Since SYS IV-VII are sub-Nyquist sampling systems,it is seen that both sampling rate (one channel) and overall sampling rate is lower than SYS I.The Gabor transform used in SYS VI is a conventional time-frequency analysis method.Due to the time-varying properties of the chirp-like signals considered in this paper,SYS VI obtains a better reconstruction than SYS IV and SYS V.However,Gabor transform cannot deal with the linear modulation properties of chirp-like signals.Thus,the joint sparsity of coefficient matrix in time-frequency domain is larger than FRGT.Compared with Gabor transform,FRGT can further improve the sparsity of signal representation in the joint time-fractionalfrequency domain.Therefore,SYS VII achieves the lowest reconstruction error among SYS IV-VII in both cases of“With noises”and“Without noises”.

Table 1 Sampling and reconstruction performance for different systems.

Table 2 Key parameters for real RADARSAT-1 data.
5.3.An application in SAR imaging
An immediate application of the proposed compressive sampling and reconstruction system can be found in synthetic aperture radar (SAR)imaging.SAR is an effective radar imaging technology.Typically,chirp-like signals are used in the transmitter to guarantee the high resolution of images.With respect to the azimuth,chirplike echoes are sampled in range at the Nyquist rate,which will absolutely result in high sampling rate and sample number.Fortunately,with the proposed scheme presented in Fig.5,we can achieve the sub-Nyquist sampling for chirp-like echoes with reduced sampling rate and sample number.
In this sub-section,a scene from the real RADARSAT-1 data is used to test the performance of the proposed compressive sampling and reconstruction system.The data are acquired over the parts of Vancouver,Canada.Some key parameters for real data are summarized in Table 2.For more details,please refer to the work[38].

Fig.9.SAR images with the sampling rate 9.69 MHz:(a) SYS IV,(b) SYS V,(c) SYS VI,(d) SYS VII.

Fig.10.SAR images with the sampling rate 16.16 MHz:(a) SYS IV,(b) SYS V,(c) SYS VI,(d) SYS VII.

Fig.11.SAR images with the sampling rate 22.62 MHz:(a) SYS IV,(b) SYS V,(c) SYS VI,(d) SYS VII.

Fig.12.SAR images with the sampling rate 32.317 MHz.

Table 3 Quantitatively evaluation of obtained SAR images.
For comparison,different systems,including SYS I,IV-VII mentioned in Section 5.2,are used to conduct the sub-Nyquist sampling for real data.The radar sampling rate is viewed as the Nyquist sampling rate.The total sampling times in range and azimuth are 24.75 μs and 0.6364 s respectively.Systems SYS IV-VII achieve the sub-Nyquist sampling for received chirp-like echoes.The overall sampling rates are set to 9.69 MHz,16.16 MHz,and 22.62 MHz,which are obviously lower than Nyquist sampling rate.After the sub-Nyquist sampling,BM-SBL is used to reconstruct the sparse coefficients,and then chirp-like echoes are recovered based on corresponding coefficients.After that,the typical Range-Doppler(RD)algorithm is used for imaging.The results are shown in Fig.9,Fig.10,Fig.11 and Fig.12.In Fig.12,the echoes are sampled at Nyquist rate (32.317 MHz),whereas in Figs.9,Figs.10 and 11,the echoes are sampled at the sub-Nyquist rate (9.69 MHz,16.16 MHz and 22.62 MHz respectively).For convenience,the image entropy[46] and image contrast [47] are used as two criteria to quantitatively evaluate the quality of obtained SAR images.The image entropy is defined as

where(I)denotes the obtained SAR image by different methods.Similarly,the image contrast is expressed as
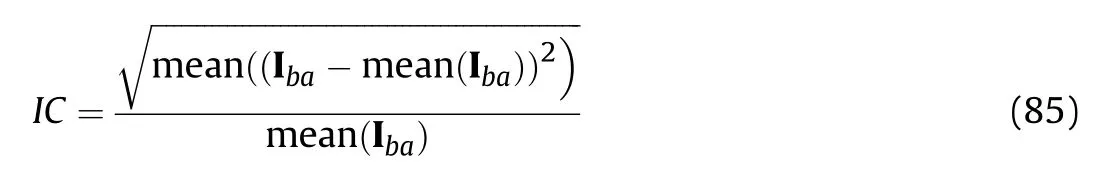
where mean(·)is to calculate the spatial mean.As indicated in the works [34],The SAR image with high quality is related to a small entropy or large contrast.The quantitatively evaluations for the obtained SAR images in Figs.9,Fig.10,Figs.11 and 12 are summarized in Table 3.
From the images,it is seen that after sub-Nyquist sampling,we can still make an effective imaging for the targets.And with the increase the overall sampling rate,the qualities of SAR images get better.This result can also be seen in Table 3.When overall sampling rate increases,IE gets smaller,whereas IC gets larger.Compared with SYS IV,SYS V and SYS VI,SYS VII achieves the better imaging.With the same sampling rate,SYS VII has a smaller IE and larger IC than SYS IV,SYS V and SYS VI.This is because that the tragets in different ranges bring an inherent time-varying properties to the chirp-like echoes.Then benefitting from the sparser representation in the joint time-fractional-frequency domain,the proposed scheme based on FRGT makes a better reconstruction for the time-fractional-frequency coefficients.That contributes to the better recovery for echoes,and eventually results in the better imaging.
6.Conclusion
In this paper,we consider the problem of sampling and reconstruction for time-varying chirp-like signals.Our proposed scheme is based on the CS and SI space theory.We propose a compressive sampling and reconstruction system to achieve the sub-Nyquist sampling and accurate reconstruction for time-varying chirp-like signals.
The proposed scheme is conducted on the SI space associated with FRGT.Motivated by a novel STFRFT,the conception of FRGT is introduced.We analyze the completeness of FRGT and construct a filter bank to obtain the time-fractional-frequency coefficients.The sub-Nysuist sampling and accurate reconstruction is achieve by the proposed compressive sampling and reconstruction system.We establish the reconstruction model and propose the BM-SBL algorithm to improve the reconstruction performance.We analyze the total recontruction error for the whole system.It is shown that a bounded recontruction error can be obtained with considerations of noises and mismatches.The effectiveness of the proposed scheme is verified by numerical experiments.We show that the proposed system outperforms the other systems state-of-the-art.In addition,an immediate application in SAR imaging is presented for the proposed system.We show that the effective imaging for the targets is achieved even the sampling rate is lower than Nyquist rate.
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
This work is supported by National Natural Science Foundation of China (Grant No.61501493).
Proof of Theorem I
Assume that γ(t)is a frame with the bounds Aand Bsatisfying
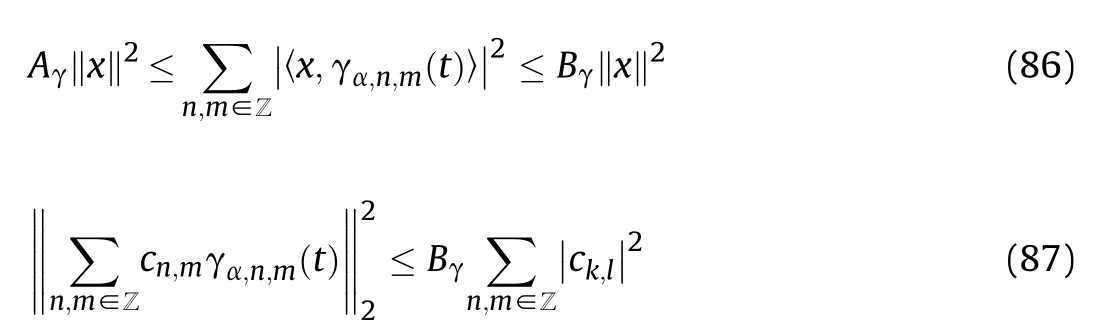
The error caused by the mismatch is depicted by
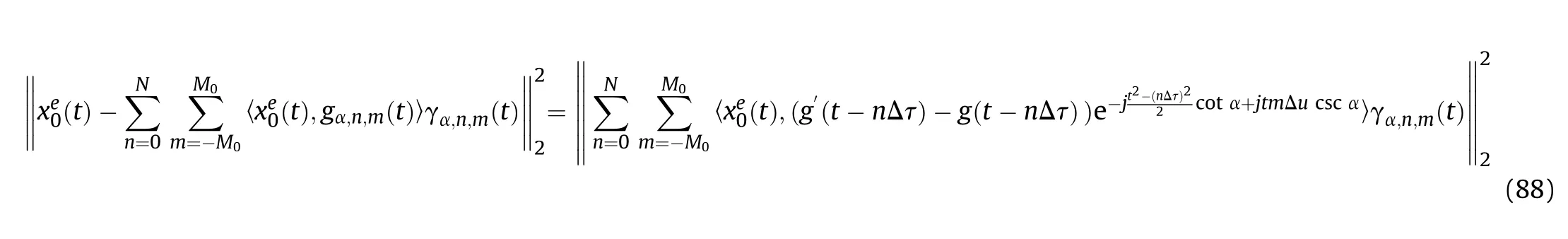
With the equation in (87),we have
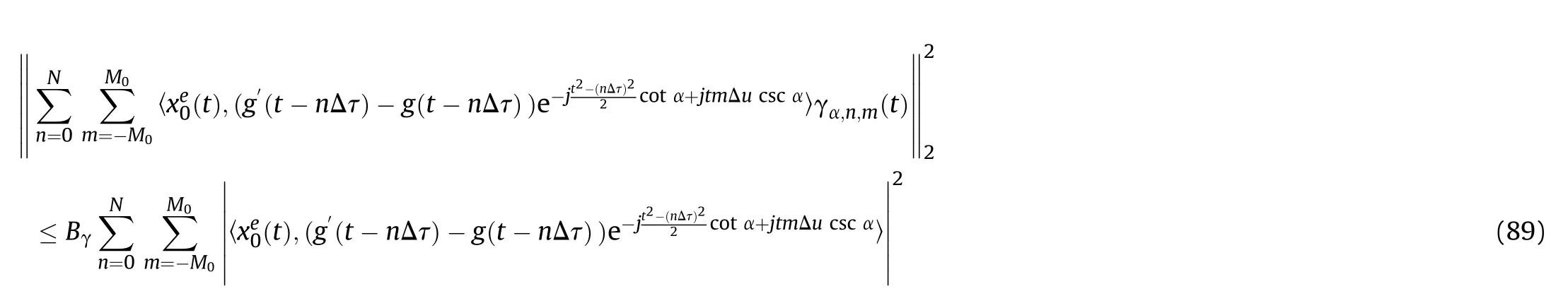
According to(77),the following result is obtained

Then Theorem I is proven.


Proof of Corollary I
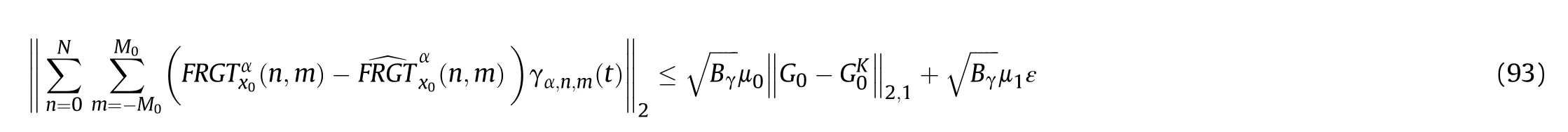
According to(87),we have
With (73),it is obtained that
Meanwhile,
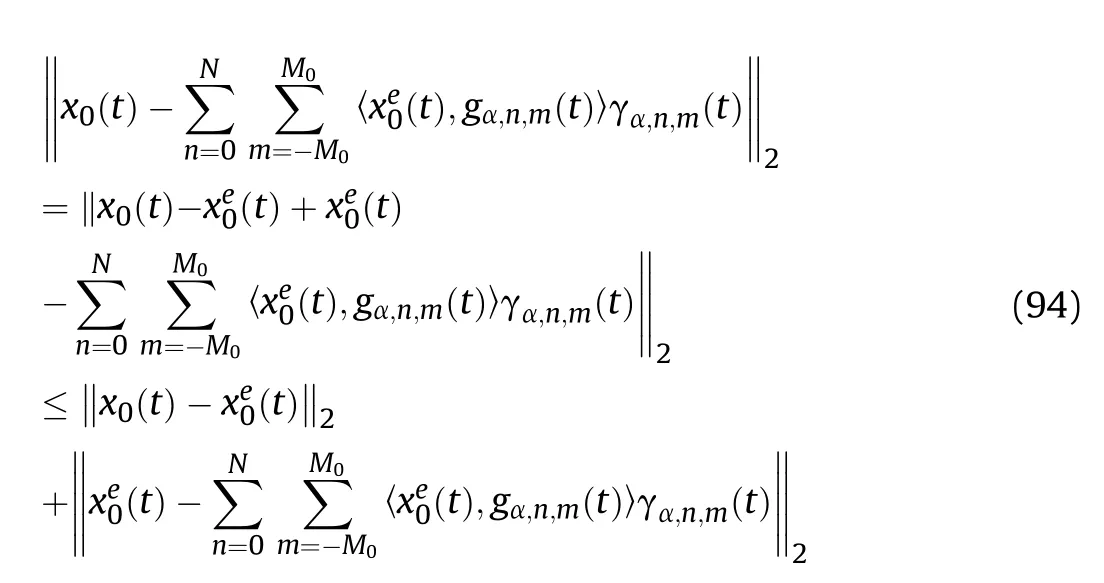
According to Eq.(75) and Theorem I,we have
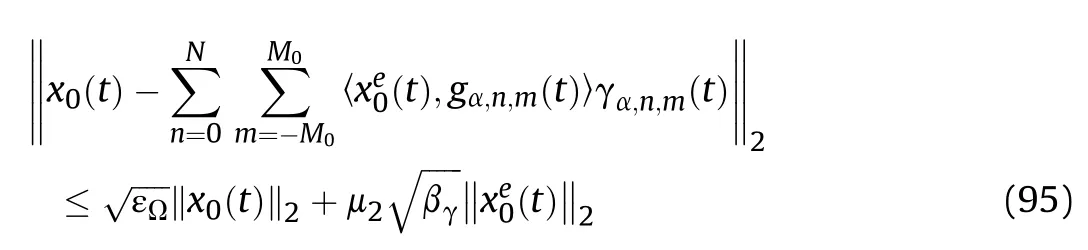
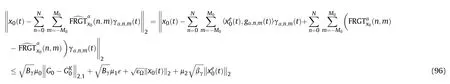
Therefore,the total error is depicted as
杂志排行
Defence Technology的其它文章
- Effect of porosity on active damping of geometrically nonlinear vibrations of a functionally graded magneto-electro-elastic plate
- Theoretical predict structure and property of the novel CL-20/2,4-DNI cocrystal by systematic search approach
- Effect of different geometrical non-uniformities on nonlinear vibration of porous functionally graded skew plates:A finite element study
- Manipulator-based autonomous inspections at road checkpoints:Application of faster YOLO for detecting large objects
- Penetration and internal blast behavior of reactive liner enhanced shaped charge against concrete space
- Failure investigation on high velocity impact deformation of boron carbide(B4C)reinforced fiber metal laminates of titanium/glass fiber reinforced polymer
