Calculating detonation performance of explosives by VLWR thermodynamics code introduced with universal VINET equation of state

Qin Liu ,Ying-ling Dun ,Wei Co ,Hong-ho M ,Xin-ping Long ,Yong Hn ,*

a Institute of Chemical Materials,China Academy of Engineering Physics,Youxian District,621000,Mianyang City,Sichuan Province,China

b CAS Key Laboratory of Mechanical Behavior and Design of Materials,Department of Modern Mechanics,School of Engineering Science,University of Science and Technology of China,Hefei,Anhui,230026,PR China

c China Academy of Engineering Physics,Youxian District,621000,Mianyang City,Sichuan Province,China

d Key Laboratory of Fire Science,University of Science and Technology of China,Hefei,Anhui,230026,PR China

Keywords:Detonation performance Thermodynamic calculation VINET equation of state VLWR thermodynamics Code Support vector machine Cylinder test

ABSTRACT Thermodynamic calculation is the theoretical basis for the study of initiation and detonation,as well as the prerequisite for forecasting the detonation performance of unknown explosives.Based on the VLWR(Virial-Wu)thermodynamic code,this paper introduced the universal solid equation of state(EOS)VINET.In order to truly reflect the compressibility of nanocarbon under the extremely high-temperature and high-pressure environment in detonation,an SVM(support vector machine)was utilized to optimize the input parameters of carbon.The detonation performance of several explosives with different densities was calculated by the optimized universal EOS,and the results show that the thermodynamic code coupled with the universal solid EOS VINET can predict the detonation performance parameters of explosives well.To investigate the application of the thermodynamic code with the improved VINET EOS in the working capacity of explosives,the interrelationship between pressure P-particle velocity u and pressure P-volume V were computed for the detonation products of TNT and HMX-based PBX (HMX:binder:insensitive agent＝95:4.3:0.7) in the CJ isentropic state.A universal curve proposed by Cooper was used to compared the computed isentropic state,where the ratio of pressure to CJ state were plotted against the ratio of velocity to CJ state.The parameters of the JWL(Jones-Wilkins-Lee)EOS for detonation products were obtained by fitting the P-V curve.The cylinder tests of TNT and HMX-based PBX were numerically simulated using the LS-DYNA,it is verified that,within a certain range,the improved algorithm has superiority in describing the working capacity of explosives.

1.Introduction

The accurate modelling of the thermodynamics of detonation products is a fundamental premise to evaluate the damage capability of explosives and guide the design,development and optimization of weapon charges.A fluid phase composed of simple molecules (CO,HO,N,…) will generate when the CHON molecular systems decomposes,and a solid phase containing numerous carbon nanoparticles is accompanied in case of negative oxygen balance[1].The fluid phase can be modelled in two definite paths:first using molecular simulations,a theoretically accurate but computationally expensive method [2],second using a thermochemical code based on statistical physics[3].The latter is used in VLWR(Virial-Wu)[4,5],which is applicable in the pressure range from atmospheric pressure to nearly 100 GPa with no empirical parameters,the free energy of complicated molecular mixtures is based on the ideal contribution of the decomposition into each pure substance and an additional contribution due to the intermolecular interactions.This additional contribution is firstly modelled by a sum of Lennard-Jones potentials,then lessened to a single effective fluid using a mixing rule.The thermodynamic code can reproduce experimental or literature values with relatively small errors.

In the case of CHON explosives with a negative oxygen-balance,one must calculate the thermodynamic contribution of the solid carbon phase.So far in VLWR,the carbon nanoparticles were simulated by an effective condensed phase made of graphite,diamond,and liquid carbon [6]:Its free energy was given by a semiempirical multiphase equation of state(EOS),namely Cowan EOS.It requires 12 parameters that is cumbersome and adopts relatively old shock compression data based on bulk carbon,it also limits the ability of VLWR to predict the properties of an explosive not in the fitting code.Thus further efforts are required to obtain a more generic EOS for carbon.In this paper we use a concise universal VINET EOS to describe the thermodynamic condition of carbon.The description of the EOS for solids is broadly divided into two types:the first uses finite stress-strain relations to find reliable methods of fitting curves (e.g.,the Birch-Murnaghan equation [7]),and the second proposes models based on the energy corresponding to different classes of solids.According to the derivation by Vinet et al.[8-10],for different condensed solids,an uniform form of the P-V relation exists,namely VINET EOS,which can be applied to various condensed-phase media over a wide range of temperatures and pressures [8,11],including ionic crystals,metal crystals,covalent crystals,and noble-gases.It has been shown to describe shock Hugoniot data of graphite well [12] and its accuracy exceeds the Murnaghan and Birch equations,especially in highly compressed states where no additional tunable constants are required.As with the Murnaghan EOS [7],it requires very few parameters.

Due to the pressure and temperature characteristics of the detonation process up to tens of GPa and thousands of K,the solid products do not necessarily exist in the traditionally recognized bulk form,and extreme thermodynamic conditions give rise to the generation of nanocarbon,especially for highly oxygen-lean explosives [1].Experiments and theoretical calculations show that there is a phase change and agglomeration process in the carbon product of the explosive detonation process [13-15],which plays an important role in determining many of their properties,particularly the energy release characteristics and possible failure behavior and sensitivity [13,15].The actually collected carbon product is confirmed to be either fluffy and porous amorphous graphite wrapping diamond core or complex graphitic structures such as nanometric ribbons and fullerenes,depending on the specific explosive compositions and detonation conditions[16-22].Therefore the input parameters of the VINET equation calibrated by conventional shock compression experiments on bulk carbon do not necessarily match the realistic detonation environment.To reproduce the real thermodynamic environment more accurately,this paper chooses to optimize the input parameters by SVM (support vector machine).SVM is a generalized linear classifier that performs binary classification of data according to supervised learning,and its decision boundary is the maximum-margin hyperplane for solving the learning sample [23].It is a sparse and robust classifier that uses a hinge loss function to compute empirical risk and adds a regularization term to the solution system to optimize structural risk.The final decision function of SVM is determined by only a small number of support vectors,and the complexity of calculation depends on the number of support vectors,not the dimensionality of the sample space,which avoids the“dimension disaster”in a sense.It has already been applied in image-based analysis and classification tasks,geo-spatial databased applications,text-based applications,computational biology,security-based applications,chaotic systems control,etc [24-28].

For the verification of the application ability of VINET EOS,the calculation of detonation parameters and CJ isentropic state were carried out.The calculation of the CJ isentropic state includes the comparison with the cooper curve and the contrast of displacement histories and velocity-displacement relationship between experimental and calculated results in cylinder experiment.The cooper curve is a universal relationship proposed by cooper to describe the ratio of pressure relative to CJ point changes with the ratio of relative CJ point velocity[29].Cylinder test[30,31]is a standardized experiment specially used to determine the parameters of the JWL(Jones-Wilkins-Lee) EOS of the detonation product and evaluate the working capacities of the explosive,JWL EOS is a kinetic procedure proposed by J.W.Kury et al.[32] that can more accurately describe the dynamics of the detonation product's driving and working capacities without explicit chemical reactions.

This work aims to present a universal VINET EOS based on optimization of SVM coupled with the VLWR thermochemical code and to verify the application ability of VINET EOS.The calculation of detonation performance parameters with different densities of highly oxygen-lean explosives and high explosives and verification of working capacity(TNT with a density of 1.634 g/cmand HMXbased PBX with a density of 1.863 g/cm) were implemented.The interrelationship between pressure P-particle velocity u and pressure P-volume V was calculated for the detonation products of TNT and HMX-based PBX(HMX:binder:insensitive agent＝95:4.3:0.7)in the CJ isentropic state.The computed isentropic state was compared with Cooper curve.The parameters of the JWL EOS for detonation products were obtained by fitting the P-V curve.The LS-DYNA program was applied to numerically simulate the cylinder test of TNT and HMX-based PBX explosives to verify the effectiveness of the improved algorithm in describing the working capacities of explosives.

2.Theoretical formulation

2.1.General description of the VLWR code

VLWR is used to calculate the thermodynamic properties of a mixture with a known composition ratio,which contain gases,liquids,and solids [4,5,33].The equilibrium composition of chemical substances is calculated from the minimum Gibbs free energy and the number of moles of chemical elements (stoichiometric conditions).The second-order virial coefficient of the VLWR state equation is obtained by theoretical calculation,and the third,fourth,and fifth terms are based on the similarity of the virial coefficients at high-temperatures,using the van der Waals equivalent fluid model of one-component (vdwlf) for the gaseous detonation products.The complete expression of VLWR is:

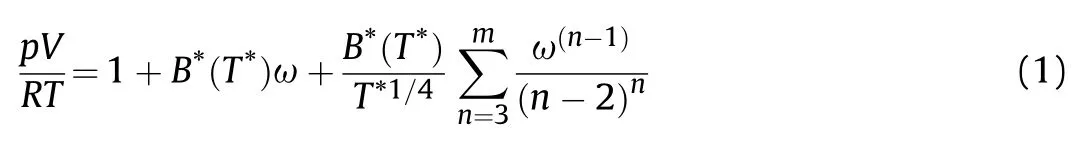
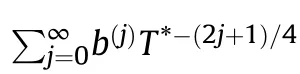
2.2.Explanation of the VINET solid state equation

Vinet[8-10]et al.developed a universal EOS that can be used in various condensed phase media.For metallic and nuclear materials,there is a general relationship between the total energy and the inter-atomic separation distance:

The pressure is obtained from the volume partial derivative of formula (2):

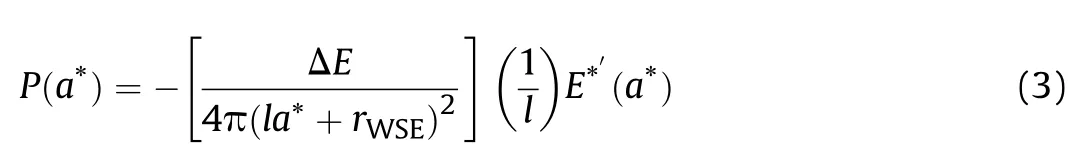
Using Hooke's law near the equilibrium point F（a）∝a,define a unified pressure function:

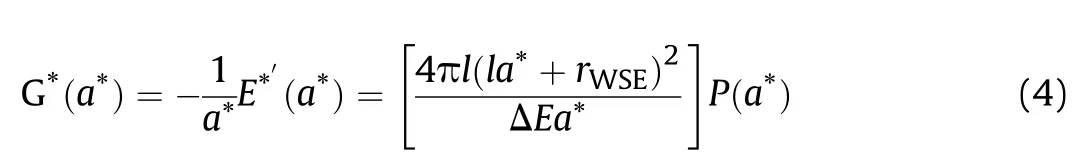
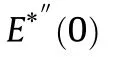
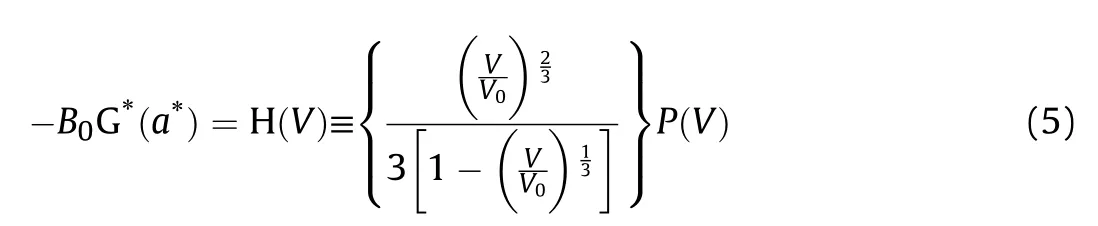
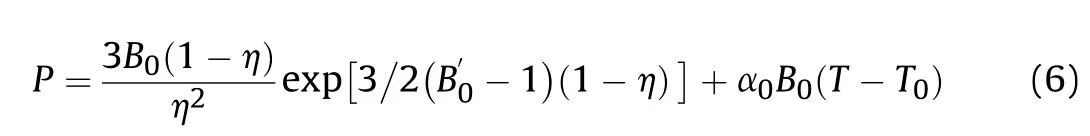
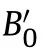
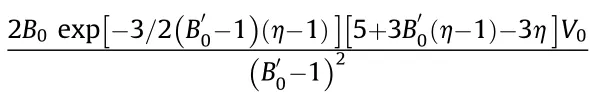
2.3.Coupled the VINET EOS with VLWR thermochemical code

The VINET EOS (Eqs.(6)-(9)) are integrated in a separate subroutine which is coupled with thermochemical code VLWR.VLWR calculates the volume,concentration and thermodynamic parameters of reaction products,for a given pressure,temperature and density along the Rayleigh line (Fig.1).

By the integration of the VINET equations,the thermodynamic parameters including internal energy,enthalpy,and entropy are obtained.The self-sustaining steady-state detonation velocity,CJ pressure and temperature are calculated as follows:

●Given the initial pressure and temperature,the subroutine calculates the volume and free energy of the gas and solid product,VLWR performs thermochemical equilibrium calculation to determine the concentration of individual products based on the principle of minimum free energy,then the Hugoniot curve of the product was combined to get the actual temperature.

●Applying the parabola method to find the CJ point,search interval is gradually reduced and the one-dimensional search method is utilized to find the approximate minimum point along the Rayleigh line.Once the CJ point is determined,the corresponding detonation performance parameters are derived.

3.Optimization process of the algorithm

Recent studies on detonation synthesis of nanosized ultrafine diamonds have shown that the solid phase carbon in detonation ash is not macroscopic bulk graphite or diamond.Rather,they are nano-sized diamond,graphite,or other carbon phases.They are much smaller in size at the beginning of growth and their surface contribution is significant [19].This indicates that the EOS for carbon fitted with impact Hugoniot cannot reflect the real physical image of carbon during detonation.The carbon parameters of the VINET EOS given in the literature are calibrated by the impact compression data of bulk carbon,and in order to reflect the more realistic state of carbon in the extreme environment of detonation,this paper uses the SVM support vector machine to optimize the four input parameters of the VINET state equation.

3.1.Get training data

Fig.1.Schematic representation of the model.

3.2.Construct SVM model

The support vector machine (SVM) linear programming model[34,35] can be expressed as

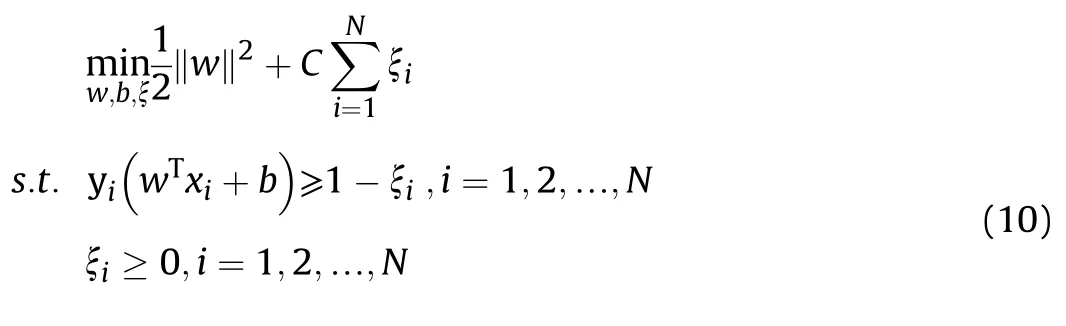
The“lower”and“high”types are composed of{V,B,α}.Here,the optimal segmentation plane can be expressed by the function f（x）＝wx+b.w is the normal vector of the hyperplane,b is the offset from the support vector to the hyperplane,x is located in the hyperplane when f（x）is equal to 0,C is a hyperparameter greater than 0,and called the penalty parameter.When the sample size does not satisfy the interval greater than 1,the relaxation variable is introduced,and its“pairwise problem”can be obtained using the Lagrange multiplier method:

Given a training sample set,the linear classifier finds a hyperplane in the two-dimensional space to separate the two classes of samples based on the training samples D＝（x，y），（x，y），…，（x，y））），y∈｛-1，1｝.Of course,there are many such hyperplanes.It is essentially a convex quadratic programming problem to find the optimal solution plane that has the best interference resistance,the largest spacing between the data on either side of the line,and the greatest“tolerance”to the limitations or noise of the training set.

3.3.Training result

Fig.2.The solving result of optimal classifying planes.(a)-(j)are the best classification planes,classification data and support vector corresponding to the detonation pressure or detonation velocity of Various explosives,(k) and (l) are the optimal classifying planes of detonation pressure and detonation velocity of TNT,TATB,DATB,TETRYL,(m) is the detonation velocity hyperplane of HMX,RDX,CL-20.

According to the constructed SVM model,the best segmentation plane is solved and plotted using Matlab,and the results are shown in Fig.2.From Fig.2(a)-(j),it can be seen that the two types of results(“low”and“high”)can be completely classified by using the SVM linear model,so the best segmentation plane is the reasonable range of values for the parameters of the VINET state equation.Besides,it can be seen that there is no consistent pattern in the interrelationship of the best segmentation planes from Fig.2(k)-(m),the specific parameters are shown in Table 1.

3.4.Data processing

In order to make the adjusted parameters{V,B,α}to satisfythe calculation of detonation parameters of similar energetic materials,the points {V,B,α} are selected to minimize sum of distance from the best segmentation planes in Fig.2(k)and(l),(m)respectively:

Table 1 Relevant parameters of the optimal classifying planes [36-37].

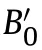
4.Specific application of explosives

4.1.Verification calculation of detonation performance of explosive

With the density of explosives changing,the corresponding detonation performance also changes accordingly,that is,their CJ detonation pressure and CJ detonation velocity are different,which corresponds to the explosive detonation products in different pressure and temperature ranges.Therefore,whether the detonation performance parameters of CHNO explosives of different densities can be accurately calculated is an effective method to test the superiority of the EOS.In order to test the superiority of the VINET EOS,the detonation performance parameters of CHNO explosives with different densities were calculated as a reference basis.The specific calculation results and analysis are shown in Figs.3 and 4 and Table 2,where scatter is the experimental value or calculated value in the literature [36,38-40],and the line is the calculated value in this article.(The detailed data is provided in the supplementary material Table 4.1).Among them,according to the level of oxygen balance and the criterion of high explosives,this article adopts low-density nanocarbon parameters for TNT,TATB,TETRYL,PETN,and HNS,that is{V,B,α}＝｛5.47981 ×e，3.0 ×e，3.0 × e｝,while for RDX,and TKX-50,high-density nanocarbon parameters are adopted that {V,B,α}＝｛3.4023 × e，65 × e，1.2 × e｝,which mainly due to a compaction effect on the product carbon under the dense thermodynamic environment with high-temperature and high-pressure,that promotes the agglomeration of carbon,and the low-density nanocarbon parameters are still used when these high explosives are in low densities.

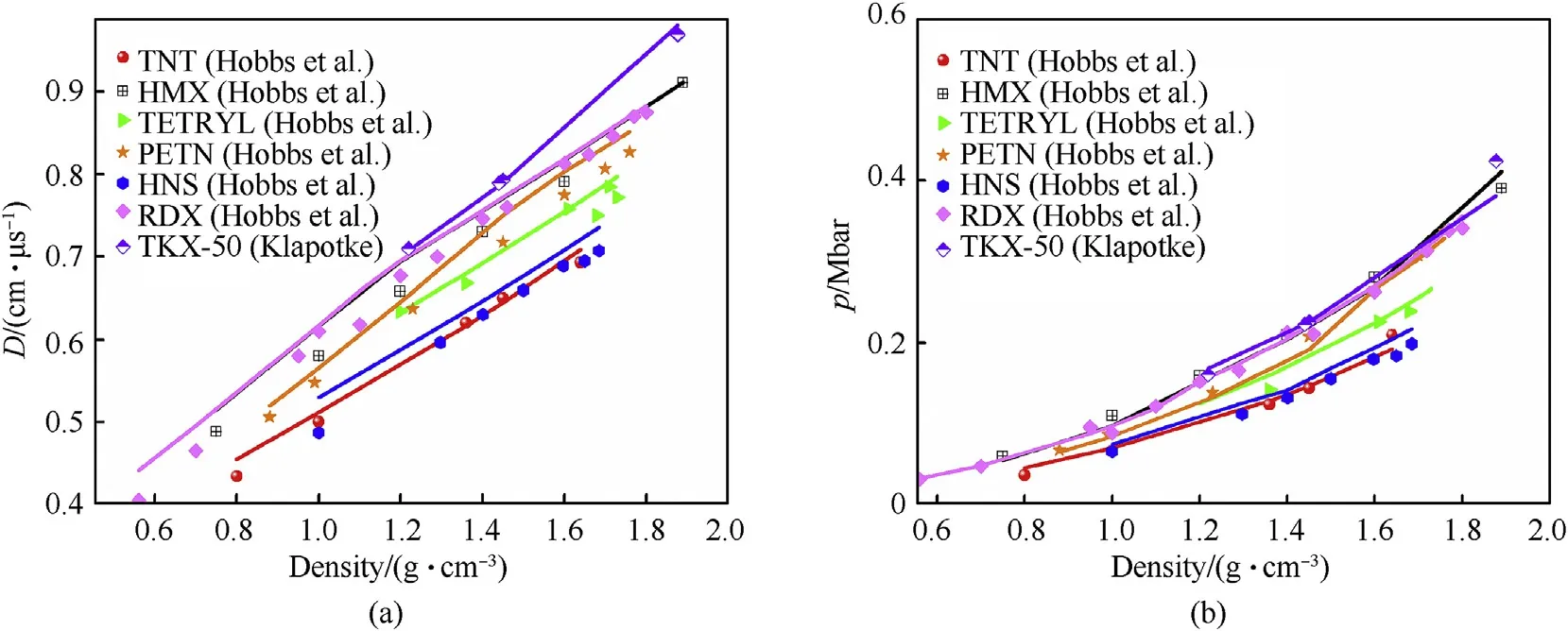
Fig.3.Comparison of the detonation velocity and detonation pressure of specific explosives between experimental and calculated results.

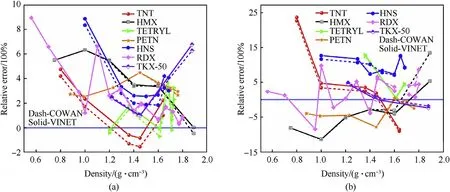
Fig.4.Relative error of specific explosives at different explosives.The dash line is for COWAN,and the solid line is for VINET.

Table 2 Error analysis of calculation results.

It can be seen from Figs.3 and 4 that in a certain density range,the thermodynamic code supplemented with the universal EOS VINET can describe the explosive detonation velocity and detonation pressure well.The error analysis in supplementary material Table 4.1 is summarized in Table 2,the maximum and minimum errors of detonation velocity for VINET are 8.94% and 0.022% for RDX of 0.56 g/cmand HMX of 1.89 g/cm,respectively,for detonation pressure the maximum and minimum errors are 23.69%and 0.0037% for TNT of 0.8 g/cmand PETN of 1.6 g/cmrespectively,where the error is defined as:（cal-exp）/exp× 100%.We also calculated the average error and RMS error for different explosives.For detonation velocity,the average error of COWAN is 2.69% and VINET is 2.98%,which indicates that the improved algorithm is slightly inferior to COWAN in velocity calculation.For detonation pressure,the average error of COWAN is 2.08%and VINET is 1.66%,so the calculation of pressure has a good improvement.Meanwhile,the root mean square error also demonstrated that the improved VINET lower the dispersion for the explosion pressure,while for detonation velocity the COWAN data dispersion is smaller.See Supplementary material for the relative value of calculation error for explosives of different densities.

4.2.The verification of working capacity

Cooper relates the pressure and particle velocity along the Hugoniot of detonation products for a series of explosive in a simplified parameter form P/Pversus u/u[29,41].The two expressions are

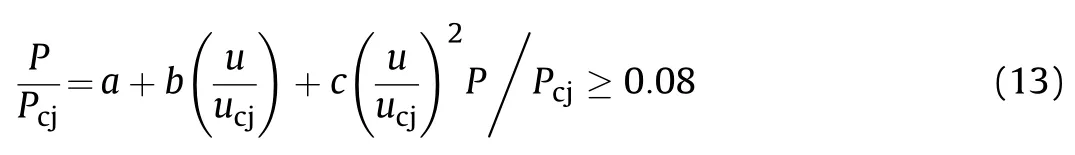
where a＝2.412，b＝-1.7315，c＝0.3195(correlation coefficient＝0.987).

where m＝235，n＝-8.71(correlation coefficient＝0.898).Here we compared the P-u curve at the isentropic expansion calculated by the improved algorithms VINET and COWAN and the cooper curve on the logarithmic axis in Fig.5 [29,42-45] to discover the associations easier.It can be seen from Fig.5 that for HMX-based PBX,VINET and COWAN are in good agreement with the cooper curve in the entire range,including experimental values.For TNT,when P/Pis lower than 0.63,the calculated value starts to deviate from the cooper curve.Since there are not enough experimental values for TNT at this density,we don't know whether the calculated values and cooper curves can accurately reproduce the experimental values.

Fig.5.Comparison of TNT and HMX-based PBX isentropic expansion data calculated by reduced parameter method and by thermodynamic code.

Fig.6.Schematic diagram of cylinder device.

Cylinder experiment schematic diagram is shown in Fig.6,the cylinder placed parallel to the stand,high-speed scanning camera through the metal plate slit was used to record the cylinder expansion distance of the stable detonation section of the explosive.

Based on the minimum free energy condition and isentropic condition S＝Sof detonation products,the pressure value of the detonation product is adjusted,and the temperature,volume and internal energy that meet the conditions are calculated according to the gas state equation VLWR of the detonation product and the solid-state equation VINET.The calculated isentropic expansion curves of the detonation product are shown in Fig.7,where for the TNT with a density of 1.634 g/cmand HMX-based PBX with a density of 1.863 g/cm.To reflect the most realistic state of the corresponding thermodynamic conditions of carbon,the input parameters of the TNT and HMX-based PBX are optimized by SVM,and the corresponding parameters with the smallest sum of the distance from the optimal plane of detonation velocity and detonation pressure are found out.The input parameters {V,B,α}are:{5.1631×e，3.0×e，2.5556×e} and {3.3473×e，65×e，1.5667×e} respectively.In Fig.7 we also draw the fitting curve of COWAN and the reference value calculated by the hydrodynamics code [46].The reference value has been compared with the experimental value and it was found that the displacement histories of cylinder wall is approximately the experimental uncertainty in the cylinder test.The calculated P-V data agrees well for TNT while for HMX-based PBX,the reference data is pure HMX,So the data fluctuates slightly.

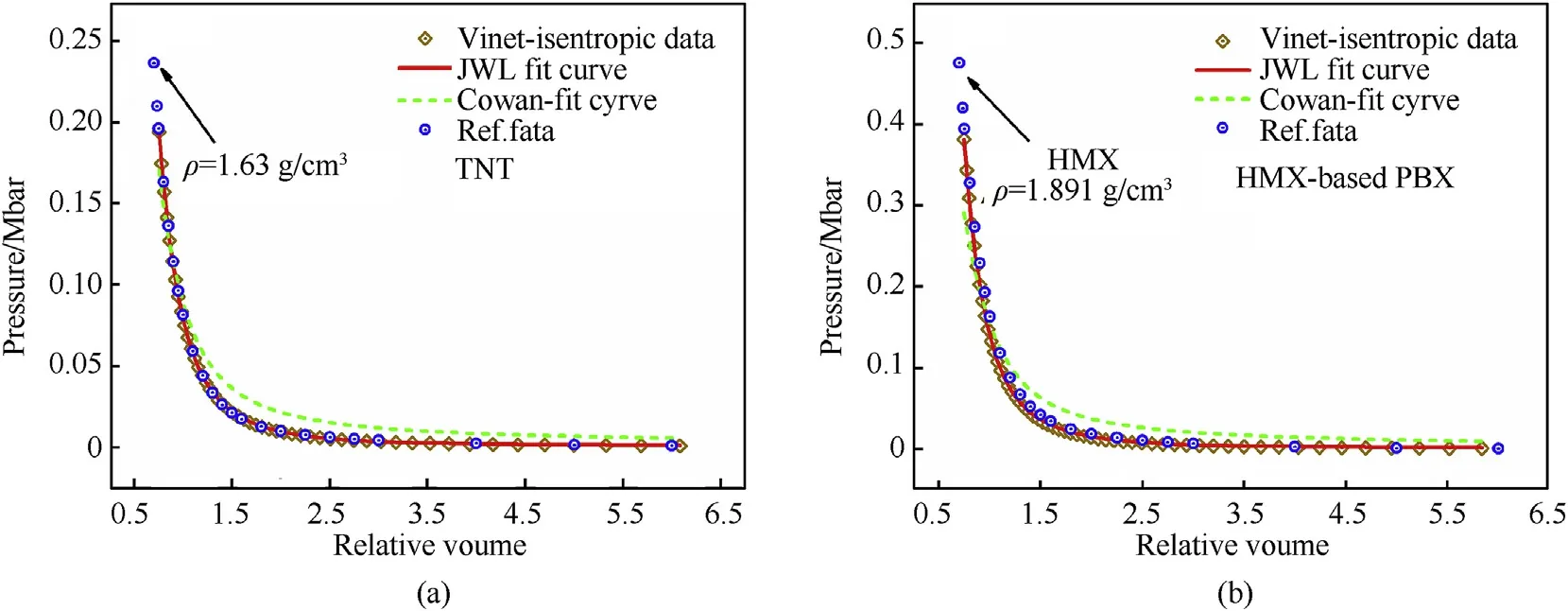
Fig.7.The calculation result of isentropic expansion curve of detonation product.

Table 3 JWL state equation parameters of detonation products of TNT and HMX-based PBX explosives.

Fig.8.Model sketch of calculation.

The specific form of the JWL state equation is:

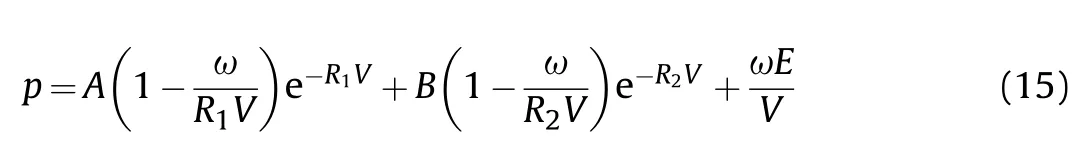
where p is the pressure of the detonation product,V is the relative volume of the detonation product,and E is the specific internal energy of the detonation product.A、B、R、R、ω are the parameters to be fitted,also called empirical(adjustment)constants.

In LS-DYNA,the definition of explosive materials needs the parameter values of A、B、R、R、ω of the JWL EOS.According to the calculated isentropic expansion curve,the parameter values of the JWL EOS of the TNT and HMX-based PBX detonation product obtained by fitting are shown in Table 3.

Based on the input parameters of the JWL EOS obtained by calculation,the LS-DYNA program was used to numerically simulate the cylinder test of TNT and HMX-based PBX explosive.The cylinder is an axisymmetric structure,and an axisymmetric calculation model can be established in the cylindrical coordinate system,as shown in Fig.8.

In Fig.8,the ABEF zone is the part of explosive in the cylinder,which adopts the point detonation method and detonates directly at point A,and the CDFG zone is the copper tube part.CF denotes the cylinder length,EF and EG is the inner diameter and outer diameter of the copper pipe.The high explosive burn model was used for explosives,and the red copper uses the John-cook material model [48],the state equation uses the Gruneisen state equation[49].The calculated values of cylinder wall velocity at the expansion distance R-R＝19 mm are shown in Table 4 for comparison with the experimental values [42].The comparison of calculated expansion displacement histories and velocity-displacement relationship are shown in Fig.9.

It can be obtained from Table 4 that the cylinder wall expansion velocities calculated by VINET and COWAN EOS for TNT is 1.15%and 1.29% respectively,while for HMX-based PBX is 0.17% and 0.99%compared with the experimental value.It can be seen that the newly introduced universal EOS can more effectively predict the velocity values of cylinder wall expansion to the characteristic distance in the cylinder experiment.Since the velocity at R-R＝5 mm and 19 mm are usually used to describe the working capacity of explosives [42],from Fig.9,the newly introduced universal EOS can better simulate the cylinder experiment of HMXbased PBX explosives in the whole range and TNT in specified limits.Combining the improved VLWR thermodynamics program with LS-DYNA can well evaluate the working capacity of explosives,which is of great significance for the synthesis design of new explosives or explosives that have not yet undergone cylindrical tests.

5.Conclusion

We coupled a universal EOS VINET with the thermodynamic code VLWR based on the Virial theory,which can be used to describe molecular crystals,ionic crystals,covalent crystals and rare gas crystals with a concise expression form and with good prediction accuracy in the whole pressure range.The generalized linear classifier support vector machine (SVM) for binary classification of data was used to optimize the initial specific volume,the initial zero pressure isothermal bulk modulus,and the zeropressure thermal expansion coefficient.And two sets of input parameters were used according to the level of oxygen balance and the classification of high explosives.The optimized thermodynamic code can describe the explosive detonation performance parameters well at different densities.The average error of COWAN is 2.69% and VINET is 2.98% for detonation velocity,while for detonationpressure,the average error of COWAN is 2.08% and VINET is 1.66%,it can be concluded that the improved algorithm is slightly inferior to COWAN in velocity calculation however the calculation of pressure has a good promotion.The root mean square error illustrated that the improved VINET lower the dispersion for the explosion pressure,while for detonation velocity the COWAN data dispersion is smaller.

Table 4 Comparison of cylinder wall velocity between calculated and test values.

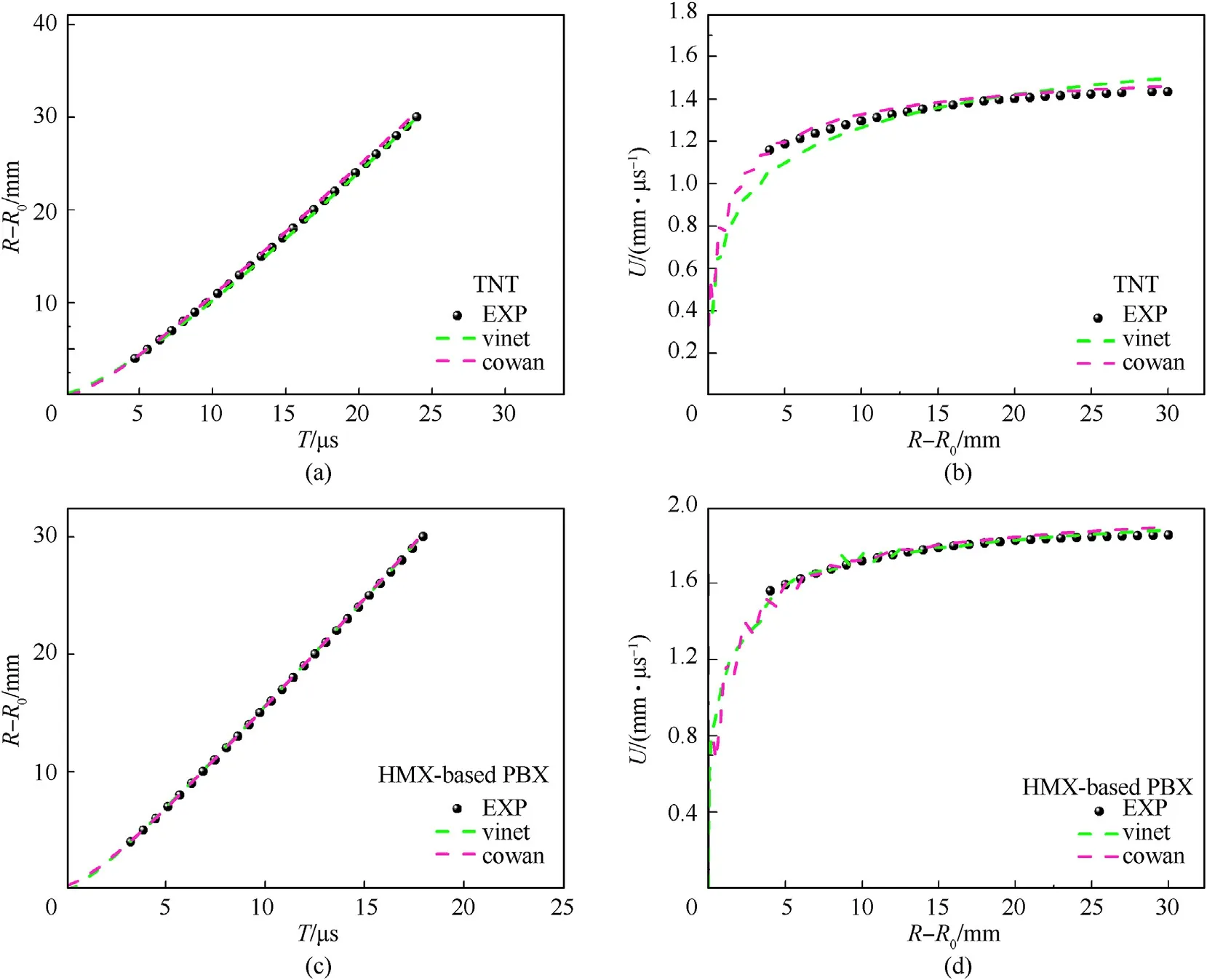
Fig.9.Comparison of displacement histories and velocity-displacement relationship between experimental and calculated results.

In the evaluation of the working capacity of explosives,the thermodynamic code supplemented with VINET and COWAN solidstate equations was used individually to calculate the isentropic expansion curve and compared with cooper curve,then the P-V curve was obtained to fit the parameters of the JWL EOS.For HMXbased PBX,the isentropic expansion curves obtained by VINET and COWAN EOS's are in good agreement with the cooper curve and experimental values in the entire range,while for TNT,there existed a slight deviations when P/Pis lower than 0.63.The hydrodynamic software LS-DYNA was used to calculate the cylinder wall expansion velocity at 19 mm,which was compared with the experimental value.The deviations for TNT and HMX-based PBX are 1.15% and 0.17% respectively.It can be seen that the newly introduced universal EOS can more effectively predict the velocity of the cylinder expansion to the characteristic distance in the cylinder test,and can well evaluate the working capacity of explosives,which provides theoretical guidance for the synthetic design of new explosives or explosives that have not yet undergone cylinder tests.

The detonation performance data of different explosives with different densities calculated by VINET and COWAN and the error compared with the experimental value are available in the supplementary material.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

We are greatly grateful for the financial support from the National Natural Science Foundation of China(No.11902298)and the National Key Research and Development Program of China(No.2017YFC0804701).

Supplementary data to this article can be found online at https://doi.org/10.1016/j.dt.2021.06.015.