基于双对数谱和卷积网络的船舶辐射噪声分类

徐源超 蔡志明 孔晓鹏

(海军工程大学电子工程学院 武汉 430033)

1 引言

卷积神经网络(Convolutional Neural Network,CNN)在图像识别领域[1,2]展现出强大的建模能力，其在船舶辐射噪声分类中的应用也取得进展。CNN在分类任务中的应用分3种：一是先人工提取特征，然后将CNN作为分类器；二是利用CNN进行特征提取；三是将原始目标信号输入CNN，构建端到端的分类模型。王念滨等人[3]将MFCC(Mel-Frequency Cepstral Coefficients)特征输入CNN，提出了结合注意力机制的快速降维卷积模型。MFCC特征最初用于语音识别，其滤波器组的中心频率和带宽根据人耳听觉特性设计。船舶辐射噪声特征信息多集中于低频线谱，甚至低于人耳听觉频率下限，因此直接将MFCC用于船舶辐射噪声会丢失信息。Shen等人[4]以时域信号为输入，利用Gammatone滤波器组初始化第1层卷积核并构建端到端的CNN。Gammatone滤波器经训练后虽然提高了识别性能，但是增加了过拟合的风险；且也是根据人耳听觉原理设计。Hu等人[5]以时域信号输入CNN自动提取目标特征，然后用极限学习机作为分类器。Li等人[6]先用不同尺寸的卷积核处理时域信号，然后在时频域上构建端到端的CNN。这些研究表明，CNN可以直接对高维的时域信号建模；但这会引入大量冗余信息，特别是高频端的冗余信息。Chen等人[7]利用卷积自编码器在低频分析记录(LOw Frequency Analysis Record, LOFAR)中提取特征用于目标分类。王念滨等人[8]和Chen等人[9]也以LOFAR输入CNN。Zhang等人[10]则将包括LOFAR在内的多种谱输入CNN。这些方法把LOFAR看作2维图像输入CNN，其在频率方向上均采用线性坐标。考虑由同一噪声源激发的谐波特征(以下称同源特征)，当基频变化时，各次谐波特征在线性频率坐标上的变化距离不等，这与卷积层对输入的平移等变性不适配。平移等变性[11]是指，当输入平移时函数输出也做相等平移。线性频率坐标的功率谱输入CNN时，当噪声源工况变化，其“激活”的卷积核不同。

对数频率坐标下同源特征等距变化的特点与CNN相适配。同时，对数坐标放大噪声谱低频部分信息，有利于目标分类。文献[12]发现恒Q变换(Constant Q Transform, CQT)特征比其他特征分类性能更强，其在频率方向采用对数坐标。CQT多用于音乐分析[13]，频点选取一般根据十二平均律，而船舶辐射噪声信息主要包含在低频段，且CQT特征高频端分辨率不足可能导致信息丢失，所以分析频点应更加细密。

减小对数的底可以提高频率分辨率，但同时会增加输入特征长度，导致CNN需要在深层才能对长距离依赖的同源特征建立连接。本文提出双对数谱，将分辨率很高的对数谱频点排列成矩阵，以此作为网络输入可以兼顾保留信息和控制CNN深度及参数规模。针对辐射噪声双对数谱的各行表征同一目标的特点，设计一种集成卷积网络(Aggregating CNN, ACNN)，使各行输入共享网络参数。进一步地，在损失函数中加入深层特征距离损失作为约束惩罚项，提高了分类正确率。

2 模型

2.1 船舶辐射噪声特征

2.1.1 平移等变性

图1为某船LOFAR，可以观察到一组同源特征(图中红色方框)。参考白色辅助线，当船舶工况变化时，线性坐标下线谱间的距离随之变化，特征尺度变大；对数坐标下同源特征的尺度则保持不变。CNN的卷积核用于在输入的不同位置检测特定特征。图2是线性坐标下，同源特征激活CNN神经元的示意图。工况1时，同源特征基频较小，3根线谱的间距较小，激活第1层的卷积核1。工况2时，同源特征基频增大，3根线谱间距变大，这组特征首先激活第1层的卷积核2，而后激活第2层的卷积核3。线性坐标下，不同工况的同源特征激活的神经元不同，这种情况不利于CNN层次化地提取目标特征。若在对数坐标下，由于同源特征尺度不变，两种工况下同源特征激活的卷积核相同，仅是输出产生了与输入相等的平移(即平移等变性)，这有利于特征的表达。

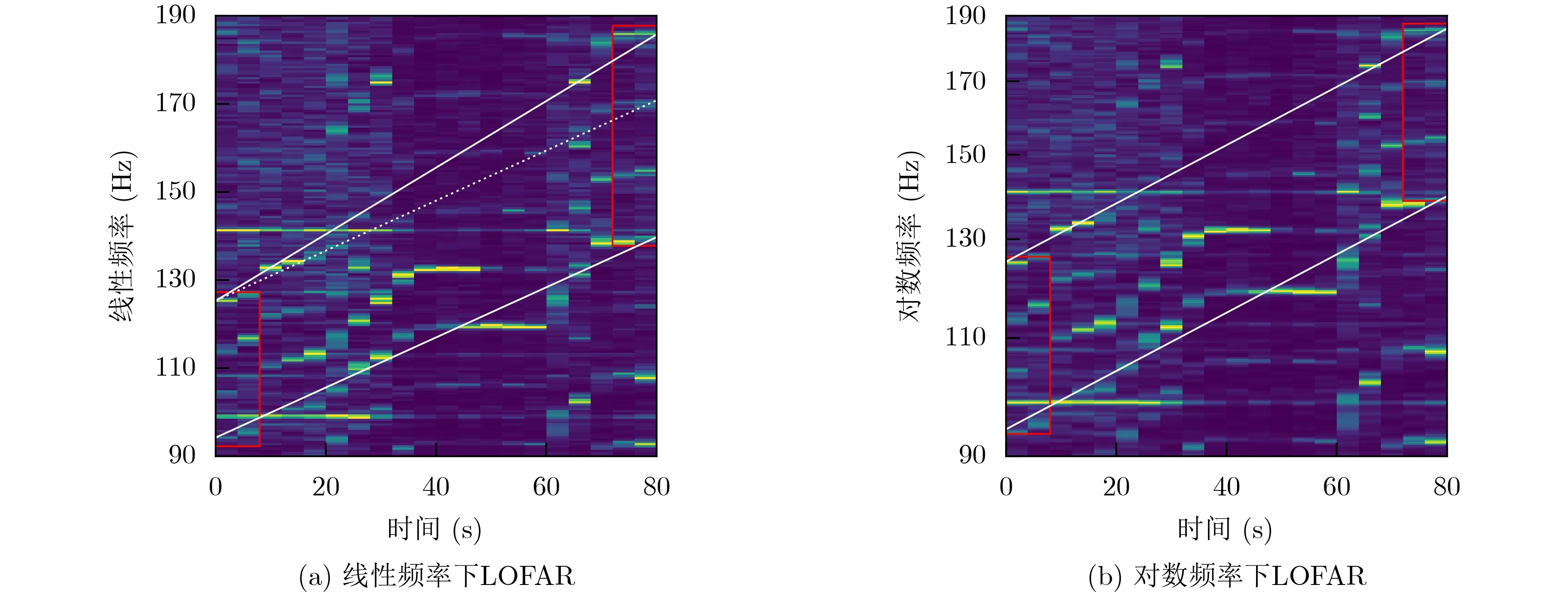
图1 工况变化时，同源特征在线性和对数频率下的表现

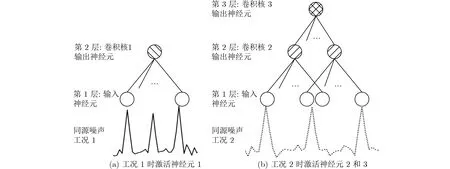
图2 线性频率坐标下同源特征激活神经元不同

CNN中的卷积运算定义为

2.1.2 双对数谱

两个频率间隔很大的相关特征要在深层才能建立连接，位于边缘的特征对输出的影响很小，CNN难以捕捉输入特征的长距离依赖-位置相距很远且非独立的特征。文献[14]指出CNN的有效感受野小于理论感受野，在CNN的深层特征图中，输入的影响随其与中心的距离增加而减小，且层数越多这种情况越严重。双对数谱把增加的频点放在列方向上以避免一个方向上的维数太多，一定程度上规避了CNN对长距离依赖建模能力不足的问题。以下介绍双对数谱的计算过程。首先计算线性谱(图3(a))，然后将其转为对数谱(图3(c))。考虑[fmin,fmax]频率范围内取M个频点的作为输入特征，则对数坐标的底为

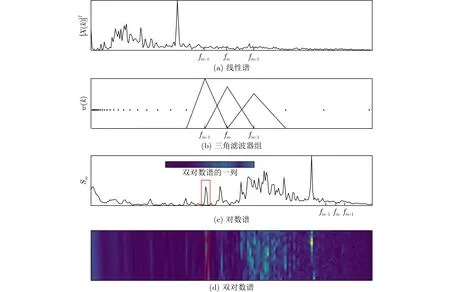
图3 双对数谱处理流程

2.2 分类模型

2.2.1 网络结构

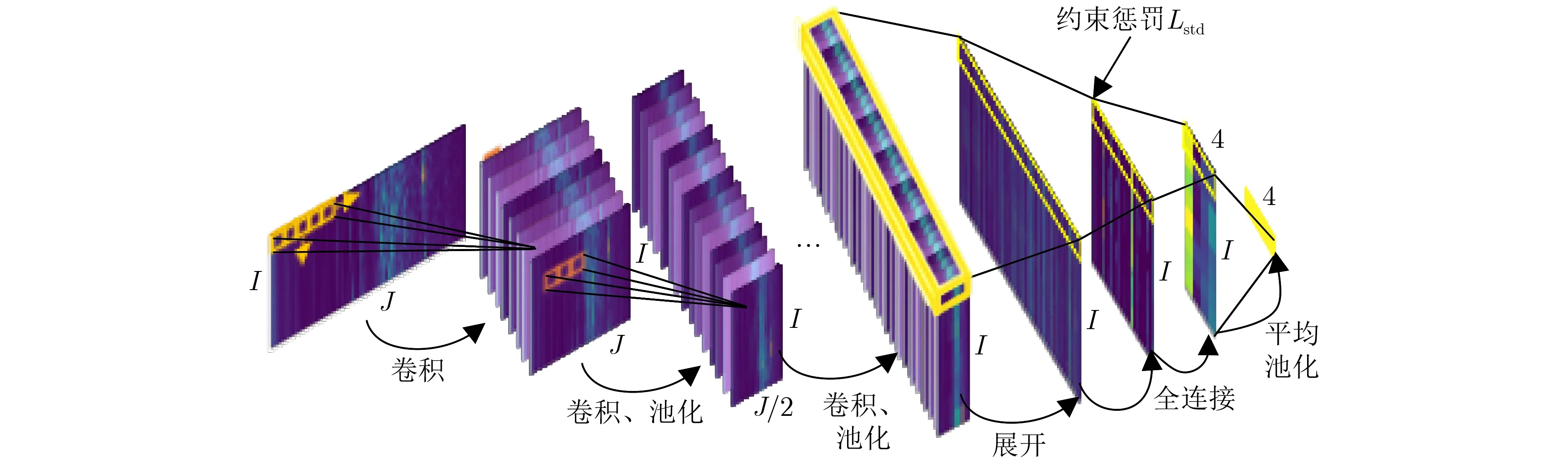
图4 集成卷积网络(ACNN)结构

2.2.2 损失函数

3 方法

3.1 数据集和预处理

本文基于DeepShip[12]数据集验证分类算法。

3.2 模型参数设置

表1 DeepShip 数据集样本统计

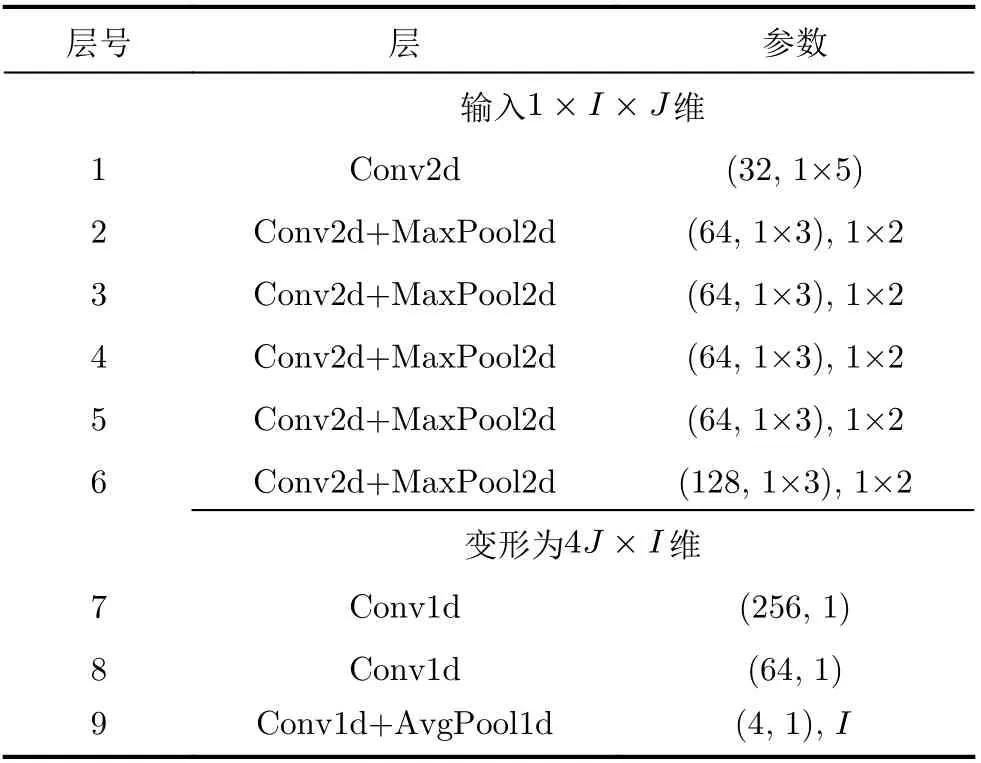
表2 ACNN 的网络结构参数

对照组CNN结构参数如表3所示。针对1维谱(包括线性谱和对数谱)，用1维卷积网络(CNN1d)作为分类器；针对双对数谱，用2维卷积网络作为分类器(C N N 2 d)。需注意，与A C N N 不同，CNN2d将双对数谱当作普通2维特征(类似图像)，从第1层开始就使用2维卷积。表中展示CNN各层卷积核数目，“CNN1d-256维”、“CNN2d”第1层卷积核尺寸分别为5和3×5，其余卷积核尺寸均为3；网络最后若干层使用尺寸为2的最大池化将特征维度降至1024，然后连接相同的4层全连接结构。

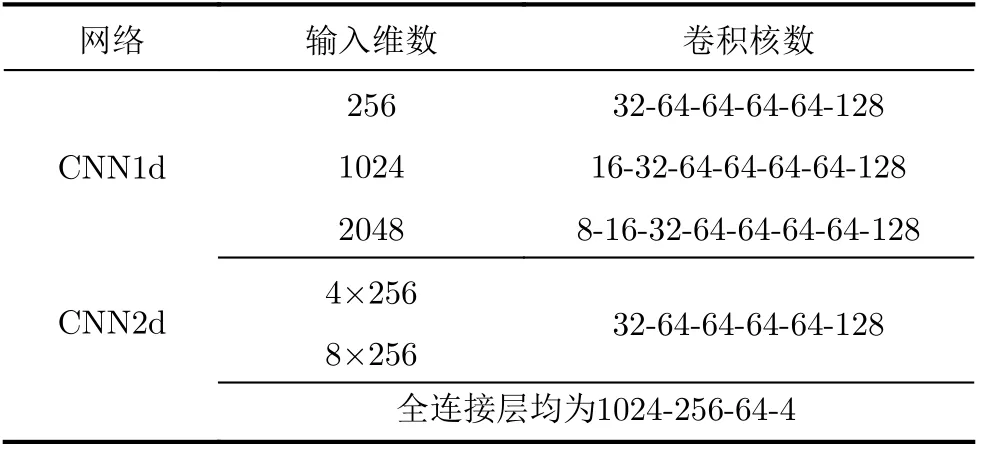
表3 对照组 CNN 结构参数

试验中所有网络均使用了批标准化和ReLU(Rectified Linear Unit)激活函数，网络输出使用Softmax激活函数，目标函数为交叉熵损失。注意，试验中ACNN与“CNN1d-256维”的网络参数量一致，ACNN在最后一层用平均池化集成了I个输出。

3.3 训练和验证

4 试验

4.1 分类性能比较

各算法分类正确率如表4所示(“ACNN”指不加约束，“ACNN+约束”指施加约束)，有如下结果：(1)对数谱特征优于线性谱。CNN1d的输入特征分别为256，1024和2048维时，对数谱的正确率比线性谱分别高1.40%, 1.55%和0.71%。256维对数谱的正确率比1024和2048维线性谱都略高。(2)对于线性谱和对数谱，CNN输入特征的维数不宜太高。无论是线性谱还是对数谱，CNN1d的输入为1024维时分类性能都是最好的。频率分辨率太低会模糊特征的频率信息，分辨率太高则会导致特征维数太高、冗余信息太多。(3)当特征维数很高时，双对数谱可以克服对数谱维数太高的问题。输入特征为1024维时，“CNN2d+双对数谱”比“CNN1d+对数谱”的正确率略低0.18%，因为此时双对数谱I=4，特征会在首行和尾行之间跳跃。而当输入特征增加到2048维时，“CNN1d+对数谱”正确率下降了，“CNN2d+双对数谱”的正确率则提高到66.35%，比前者高1.04%，表明双对数谱可以规避CNN对长距离依赖建模能力不足的问题。(4)本文提出的ACNN适配双对数谱，性能高于普通2维卷积网络CNN2d。双对数谱维数分别为4×256和8×256时，ACNN的正确率比CNN2d分别高0.79%和0.97%。(5)施加约束惩罚可进一步提高ACNN的分类性能。双对数谱维数分别为4×256和8×256时，施加约束后正确率分别提高0.25%和0.15%。

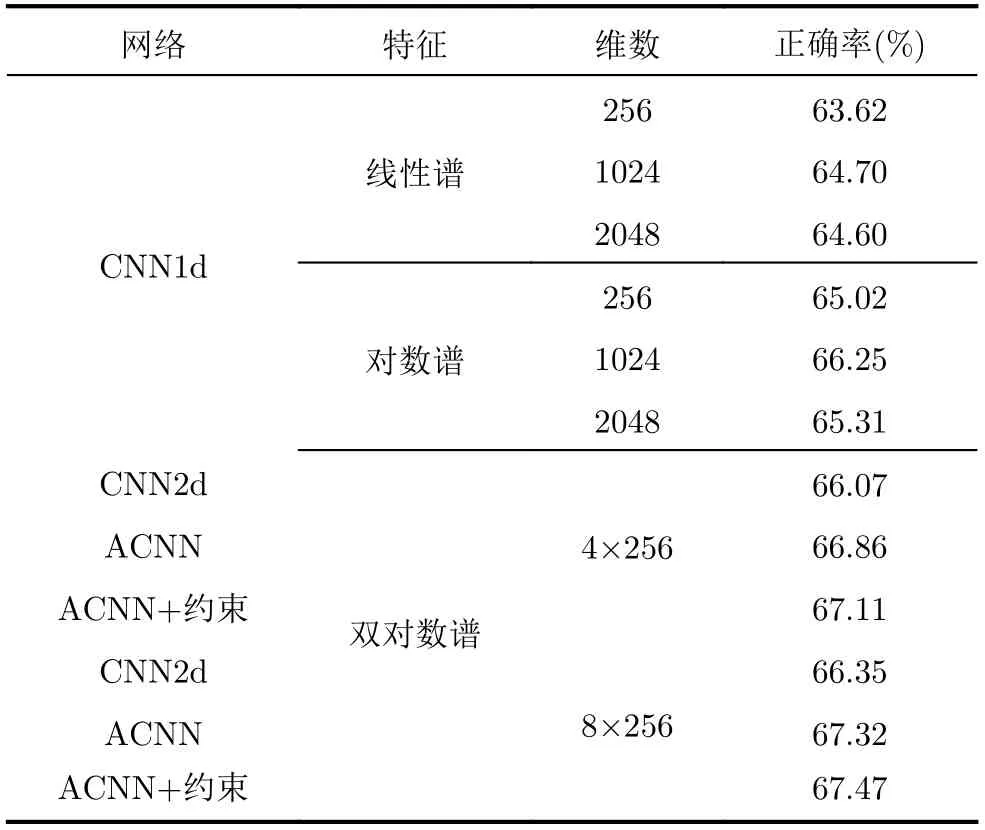
表4 分类正确率

4.2 平移等变性

利用仿真信号探究线性谱和对数谱输入下CNN的平移等变性。产生一组线性调频谐波信号

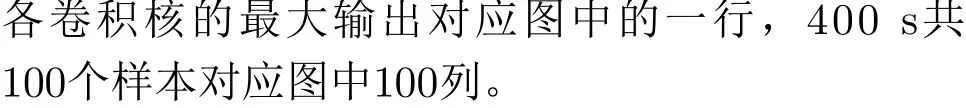
图5(a)中，线性坐标下，线谱特征随基频增加向高频端移动，同时10根线谱组成的特征尺度逐渐增加。当基频增加到原来的2倍，表达线谱特征的分辨单元数由23增加到45，相邻线谱间隔由2增加到5个分辨单元。在这个过程中，如图5(c)所示，CNN1d第1层最大输出卷积核发生变化：第0～40 s,22号卷积核的输出最大；第40～160 s, 10号卷积核的输出最大；第160～380 s, 24号卷积核的输出最大。由于第1层卷积核尺寸为5，第380～400 s后，相邻线谱间隔达到5个分辨单元，各卷积核的输出均较小，此时相邻线谱构成的局部特征要在卷积网络的下一层才能被检测到。

图5(b)中，对数坐标下，线谱特征随基频增加向高频端平移。与线性谱不同，基频增加过程中，对数谱中10根线谱组成的特征尺度保持不变，表达这个同源特征的分辨单元始终为32个左右，相邻线谱间隔的分辨单元则因线谱频率不同为1至3个不等，同阶次线谱的间隔不随频率变化。如图5(d)所示，CNN1d第1层最大输出卷积核始终为22或24号，且各卷积核输出值基本不变，这表明同源特征在对数谱中的表达方式与卷积的平移等变性相适配。

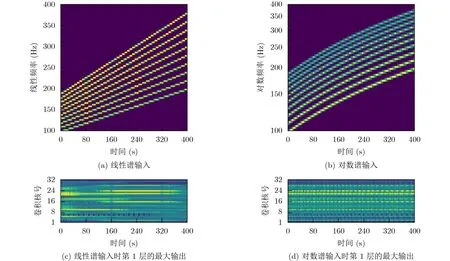
图5 卷积网络第1层的最大输出

4.3 约束惩罚系数

为考察目标函数中惩罚系数α的影响，分别设置其为0, 0.01, 0.1, 1和10，交叉熵损失LCE和深层特征距离损失Lstd随训练轮数的变化情况如图6所示，其中图6(b)中小图是第20～30轮的局部放大。

如图6(b)所示，模型在测试集上的LCE均随训练轮数增加而减小。当α=0时，即损失函数中忽略Lstd时 ，图6(a)中Lstd随训练轮数增加而增加。这表明不添加约束时，双对数谱的I个“样本”在ACNN深层特征空间中的距离会随着训练增大，这不满足I个“样本”为同一个体的先验。相应地，图6(b)的局部放大图中，α为0时的LCE大于α为0.01,0.1和1时的LCE。这表明，ACNN的损失函数中加入Lstd作为约束惩罚，有助于提高分类性能，这与4.1节的结果一致。

注意到LCE的值在1～1.3，而不加约束(α=0)时Lstd的值在0.25～1.45，二者大致处于同一量级，因此考虑设置α≤1。可以看到当α=10时，虽然Lstd被 控制得很小，但是图6(b)中LCE远高于其余曲线。这表明，损失函数中约束惩罚的比重太大，影响了模型收敛速度和分类性能。

具体地，惩罚系数α的值可通过试验确定。当α=0.01时 ，随着训练轮数增加Lstd的值逐渐增大到0.75，明显小于不加约束时Lstd的值；相应地，图6(b)中LCE的值略小于不加约束的情况。当α=0.1时，Lstd的 值先略微增大而后缓慢减小，LCE的值进一步减小。当α=1时 ，Lstd迅速减小(仅训练2轮就收敛)；此时，图6(b)中LCE的 值略小于α=0.1时的情况，且前10轮的收敛速度变慢。综上，约束惩罚系数α的值可设置为0.1～1，考虑到训练的收敛速度，4.1节分类性能比较试验中α均设置为0.1。

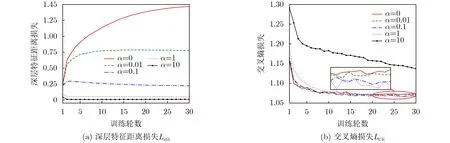
图6 惩罚系数对损失函数的影响

5 结束语

本文针对CNN的平移等变性原理，探究了线性谱和对数谱作为输入特征时的分类性能差异。结果表明，对数谱优于线性谱。针对CNN在深层才能对长距离依赖建模的缺陷，本文提出双对数谱特征。试验表明，在输入维数较高的情况下，双对数谱仍能有效建模，分类性能优于对数谱。提出的ACNN把双对数谱各行看作来自同一个体的多个样本，集成分类打分结果；构造深层特征距离损失作为约束惩罚，进一步提高分类正确率。总体上，特征为1024和2048维时，以双对数谱为输入的ACNN(加约束)的正确率，比以线性谱为输入的CNN1d分别提高了2.41%和2.87%。本文着重研究单帧谱特征作为CNN输入时的分类性能，考虑时频特征CQT的良好表现，下一步将把双对数谱拓展为时频特征。