基于辐射噪声干涉条纹斜率分布的声源深度分辨方法研究

安 良 徐若珺 曹红丽

①(东南大学水声信号处理教育部重点实验室 南京 210096)

②(东南大学信息科学与工程学院 南京 210096)

③(东南大学吴健雄学院 南京 210096)

1 引言

水中目标的航行或工作深度是其重要的属性，也是进行目标类型判别的重要依据。被动声呐作为水中非合作目标探测的重要手段之一，主要基于各种水声被动定位方法，利用目标辐射(或发射)的声信号进行目标深度估计。但是由于海洋环境的复杂性、目标信号先验信息的缺失以及声呐设备自身的限制，水中目标深度的准确估计仍是水声被动定位的难题之一。

相比于声源深度的估计，对水面目标(深度较小)和水下目标(深度较大)进行双择假设判决，可为目标类型判断提供依据，对于水下威胁目标的探测识别有重要的意义。声源的深度与简正波各阶模态的分布密切相关，现有方法大多基于简正波理论，利用声源深度与简正波模态之间的对应关系实现声源深度的二元判决。

匹配场处理被广泛应用于水声被动定位，也是研究人员最为关注的深度判别方法。杨坤德等人[1]提出基于环境扰动的线性匹配场处理方法，通过增加环境扰动约束提高方法在随机误差下的稳健性，但方法在目标方位与干扰方向相似时失效。王奇等人[2]提出基于最小二乘算法短垂线阵匹配场处理技术的目标深度辨别方法，用最小二乘得到各阶模态系数估计值重构短垂线阵测量场向量，提高了短垂线阵匹配场处理性能，但其性能在声场采样不充分时下降。Yang[3]提出基于数据的窄带信号移动源深度辨别方法，利用垂直阵接收数据提取深度函数以降低环境依赖性，但方法稳健性较低。Lin等人[4]提出基于单水听器匹配场的目标源深度辨别方法，利用频差波束形成器通过降频减小实际与模型的不匹配性，但其性能在环境变化时下降。毕雪洁等人[5]提出以垂直复声强无功分量为匹配量的目标深度匹配的二元分类方法，但方法对线谱频率稳定性要求较高。张朝金等人[6]利用半经验关系建立联合匹配定位方法，实现爆炸声源深度精确反演，但其在估计远距离目标时性能下降。

基于简正波分解的模式闪烁指数也常用于水下目标深度判别的依据。Premus等人[7,8]利用子空间投影法估计声源模态谱的差异，提出利用水平线阵进行目标深度辨别的模式闪烁指数，但方法对水平孔径有一定要求。近年来，Warping变换受到了众多学者的关注。Li等人[9]利用Warping变换提取简正波自相关与互相关指数解决波浪运动带来的源深度变化问题，并提出模式相关闪烁指数的概念。刘志韬等人[10]提出基于简正波相关项特征频率间比例关系的声源分辨方法，用Warping变换分离简正波相关项，但是方法性能在负跃层情况时降低。

近年来对干涉条纹的研究蓬勃发展，其核心思想是利用波导不变量、干涉条纹、声源径向运动速度和距离之间的关系[11]，在声场干涉结构中提取波导不变量，从而利用波导不变量的数值判别声源深度，但是这种方法需要在声源和接收器相对距离已知的条件下[12-14]。也有学者探究未知相对位置条件下波导不变量的提取：刘志韬等人[15]利用目标时延轨迹计算波导不变量，但方法要求声源相对于水听器近似匀速运动；苏冰等人[16]提出一种波导不变量β谱分离算法估计声源距离和波导不变量，但是方法只适用于波导不变量值随频率变化缓慢的情况。

本文提出了一种利用辐射噪声干涉条纹分布进行声源深度二元判决的方法。在存在负跃层的浅海波导中，利用Radon变换从干涉图像中提取干涉条纹斜率的分布，可以在未知声源距离的情况下判别声源深度。相比传统波导不变量方法和匹配场法，不需要声源距离与海洋声学环境参数的先验信息。

2 二元深度判别的基本原理

2.1 干涉条纹特征差异的物理机理

根据波导不变量理论[17]，声场干涉条纹的波导不变量可用各简正波相干项βmn加和描述。

根据文献[19]，当接收点与声源间距离足够大时，条纹的斜率近似于波导不变量。根据式(3)计算统计量svarmn，可得ω∈[ω1, ω2]频带内βmn(ω)的分布情况。波导不变量为各阶简正波相干项βmn(ω)的叠加，按式(4)定义统计量γMN，可表征一定频率范围内波导不变量的分布情况，进而反映干涉条纹斜率的分布情况，其中M,N约束了参与相干叠加的简正波的阶数范围。若γMN较小，干涉条纹斜率分布均一；若γMN较大，干涉条纹斜率分布不均。

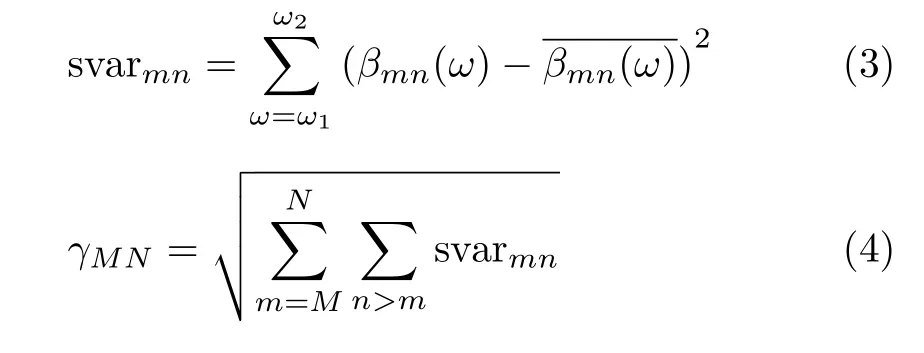
表1给出了在水深100 m，海水声速1500 m/s，海水密度1.024 g/cm3，海底声速1749 m/s，海底密度1.96 g/cm3的Pekeris波导条件下，信号频率为250～350 Hz、频率分辨率为1 Hz时声源与接收器距离为5.0～6.6 km的各阶简正波相干项βmn(ω)的统计量svarmn。将表1数据代入式(4)计算得γ14=189.91, γ59=1818.57。低阶简正波间相干的得到的统计量γ较小，而较高阶简正波间的统计量γ较大，所以低阶简正波相干形成的干涉结构斜率分布均一，较高阶简正波相干形成的干涉结构斜率分布不均。

表1 频率250～350 Hz各阶简正波相干项波导不变量的标准差svarmn

考虑有负跃层的典型浅海波导环境，声速剖面如图1所示，其中负跃层深度从15 m到35 m，对应声速分别为1515.5 m/s和1485.5 m/s，海面声速1520 m/s，近海底处水中声速1482.25 m/s，海底声速1759 m/s。

图1 典型浅海声速剖面

图2给出了频率为300 Hz，深度分别为10 m和35 m的声源激发的前10阶简正波幅度值。可见，深度10 m的声源(水面声源)激发的低阶简正波幅度小，激发的较高阶简正波幅度大。深度35 m的声源(水下声源)低阶简正波与较高阶简正波都有激发。

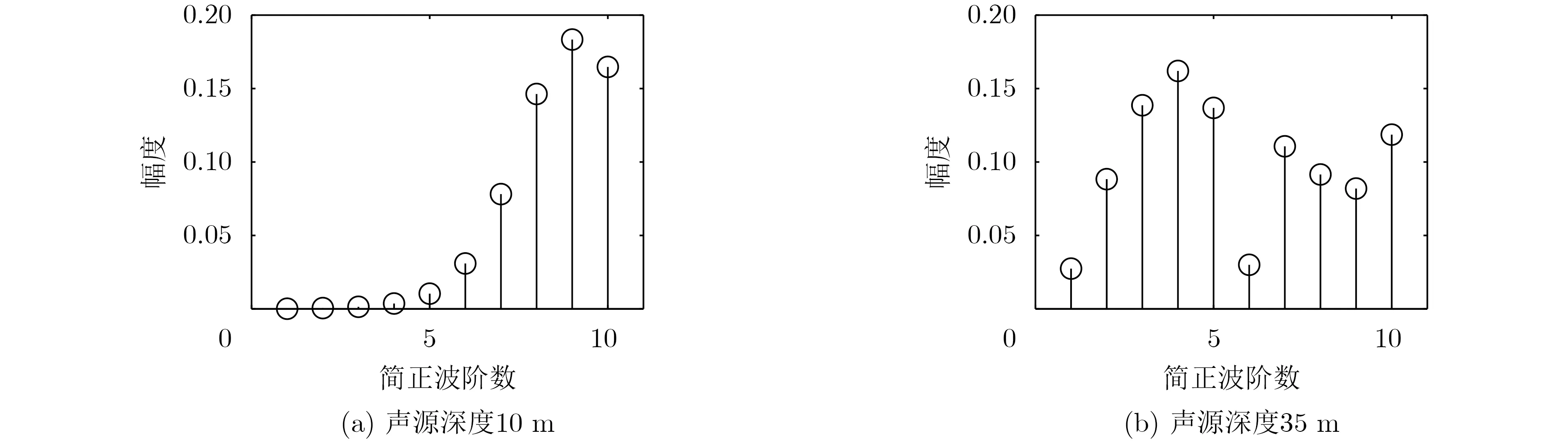
图2 频率300 Hz前10阶简正波幅度

根据前述干涉条纹斜率分布规律的分析，水面声源较高阶的简正波占主导，所以干涉条纹斜率分布不均，水下声源虽然同时激发了低阶与较高阶的简正波，但经过远距离传播后较高阶的简正波衰减较大，低阶简正波能量占比较大[16]，所以干涉条纹斜率分布均一。

2.2 干涉条纹特征提取的理论解释

由2.1节可知，声源深度的差异性会引起干涉条纹斜率分布的差异性，接下来我们试图量化这种差异性。Radon变换是一种投影方法，可以检测图像中的直线，定义为[20]

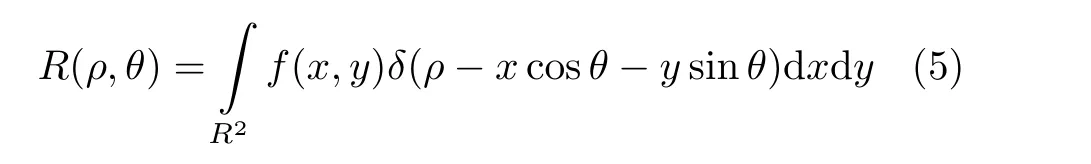
其中，f(x, y)是被积函数，x, y和ρ, θ分别为原视空间坐标和Radon空间坐标，δ(·)函数为狄利克雷函数，R(ρ, θ)为Radon变化后原函数在(ρ, θ)处的投影值。给定2维函数f(x, y)定义如下，其中ak, bk, ck为常数。

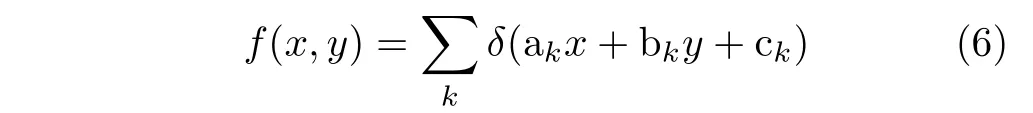
将式(6)代入式(5)，设x取值[x1,x2]，y取值[y1,y2]，Radon变换表达式可写成

设式(7)中k = 1，当tanθ ≠ b1/a1时，对于方程 δ(ρ+(c1+b1y)cosθ /a1-y sinθ) = 1，任意ρ都有y使得方程成立；tanθ = b1/a1时，当且仅当ρ = -c1cosθ/b1时方程成立。则可设

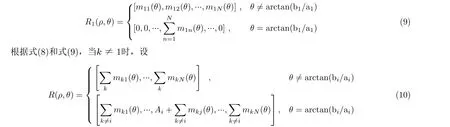
结合式(12)，当bi/ai均相同时，即空间中存在有限多相同斜率的直线，序列z(θ)有单个或较少峰值；当bi/ai不同时，即空间中存在有限多不同斜率的直线，序列z(θ)有较多峰值。定义Radon变换角度为0～180°，步长为0.1°，由式(12)计算z(θ)，结果如图3所示，图3(a)、图3(c)是Radon变换前图像，图像像素为300×300，其中图像的宽度方向对应图中x坐标，高度方向对应图中y坐标；图3(b)、图3(d)是z(θ)曲线，其横坐标为Radon变换角度，纵坐标为归一化后的z(θ)值。图3(b)、图3(d)可知，空间中直线斜率分布均一时，z(θ)为单峰或较少峰值；空间中直线斜率分布不均时，z(θ)为多峰值。由此，干涉条纹斜率的分布情况可由Radon变换后列方差向量的峰值个数表征，列方差向量z(θ)计算方法由式(12)给出。

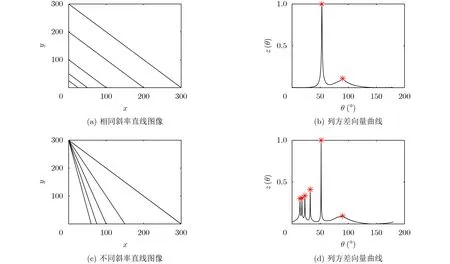
图3 Radon变换后列方差向量曲线

分析可知，列方差向量曲线的峰值个数与干涉条纹斜率的分布有关，其取决于参与干涉的简正波阶数，而参与干涉的简正波阶数与负跃层的声速梯度和声源深度密切相关。因此，可以考虑将列方差向量曲线的峰值个数作为声源深度判别的依据。

2.3 声源深度判别方法

结合2.1节、2.2节，若辐射噪声干涉条纹呈现多种斜率，Radon变换后列方差向量为多个峰值；若辐射噪声干涉条纹呈现单一斜率，Radon变换后列方差存在较少峰值。考虑与图1相同的水文环境，选取信号分析的频率范围为200～500 Hz，频率分辨率为1 Hz，假设在分析信号频带内声源信号为白噪声，接收器深度为5 m，声源深度分别为10 m(水面声源)和35 m(水下声源)，声源与接收器距离为5.0～6.6 km，距离采样间隔为1 m，利用Kraken模型仿真得到辐射噪声干涉条纹如图4所示。

图4给出了不同深度声源辐射噪声干涉条纹，其条纹斜率分布的均一性不同。利用Radon变换处理条纹图像，将变换后矩阵按式(12)求得列方差向量，得向量的峰值个数如图5所示，水面、水下目标的峰值个数分别为4个和2个，水面目标的峰值个数多于水下目标。

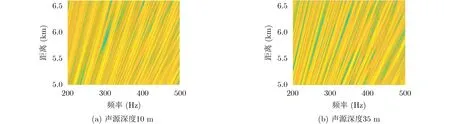
图4 不同深度声源辐射噪声的干涉条纹图像

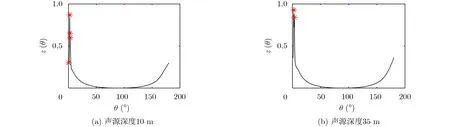
图5 Radon变换后列方差向量曲线

由前文分析可知，峰值个数与负跃层声速梯度的大小有密切联系，本文选取另两种有负跃层的典型浅海波导环境[21]，通过仿真分析负跃层梯度大小对峰值个数的影响。负跃层深度从15 m到35 m。两种环境中，15 m处声速分别为1510.5 m/s和1520.5 m/s，负跃层梯度分别为1 s-1和2 s-1，海面声速分别为1515 m/s和1525 m/s，近海底处声速分别为1487.25 m/s和1477.25 m/s，海底声速为1759 m/s。

图6和图7给出了负跃层梯度分别为-1 s-1和-2 s-1时声源信号的干涉条纹与Radon变换后的列方差向量曲线。在负跃层梯度不同时，水面水下目标噪声干涉条纹Radon变换后的列方差向量曲线峰值个数有微小变化，如梯度为-1 s-1时，水面和水下声源对应的峰值个数分别为3个和2个；梯度为-1.5 s-1时，水面和水下声源对应的峰值个数分别为4个和2个；梯度为-2 s-1时，水面和水下声源对应的峰值个数分别为4个和2个。声速剖面负跃层梯度的大小对分辨门限的影响较小。在本文后续的研究，门限值默认选取为3，即当列方差向量曲线峰值个数不小于3个时，判别对应的声源为水面声源，反之判别为水下声源。

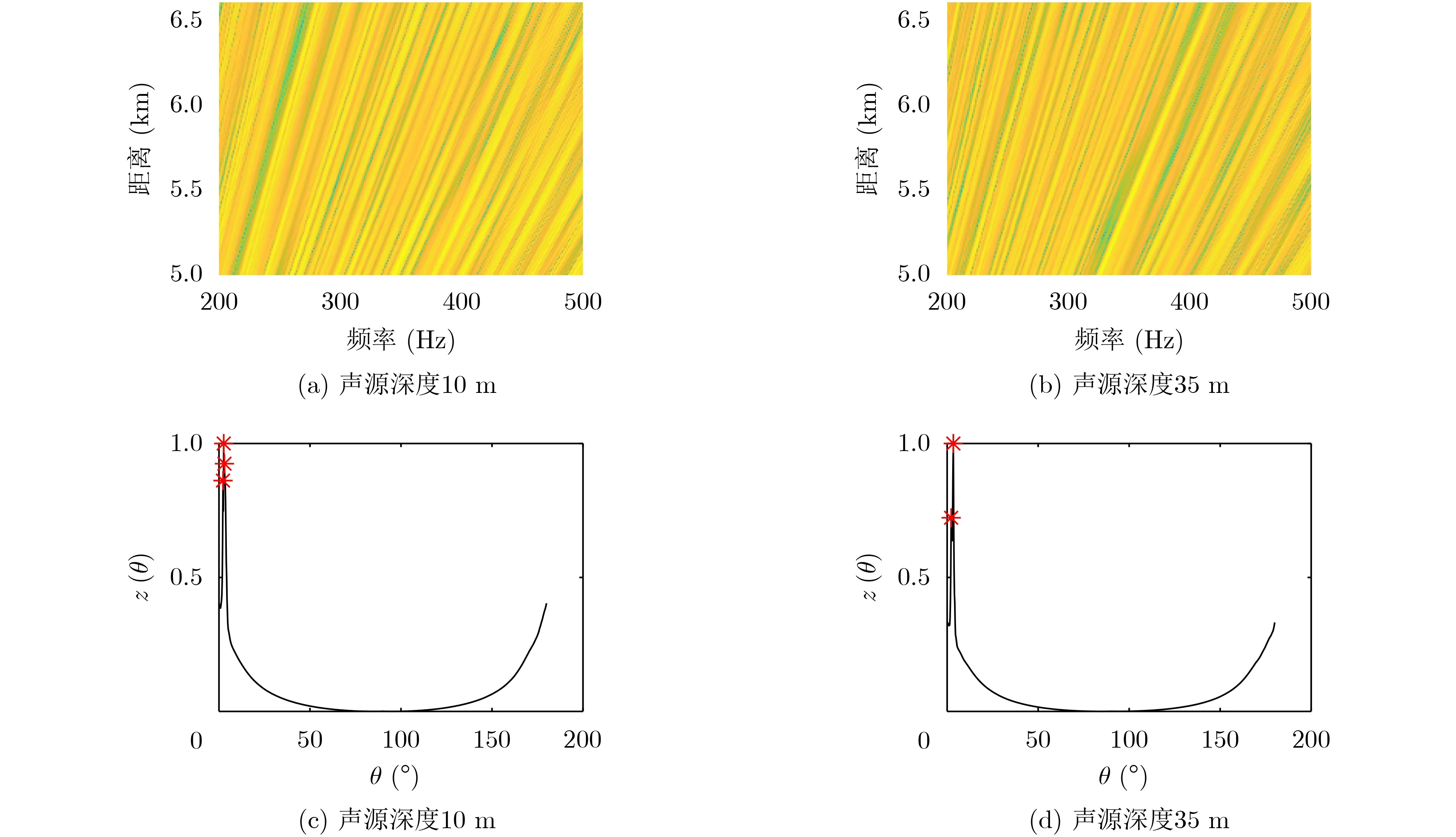
图6 负跃层梯度为-1 s-1时辐射噪声干涉条纹图像及列方差向量曲线

图7 负跃层梯度为-2 s-1时辐射噪声干涉条纹图像及列方差向量曲线

在实际海洋信道中，接收的目标信号中不可避免地会叠加环境噪声。由于海洋环境噪声级在低频段变化缓慢[22]，本文为了便于干涉特性分析，假设环境噪声在信号分析频带范围内也为白噪声，其余参数与图4和图5中参数一致。图8、图9和图10分别给出了信噪比为0 dB, 5 dB和10 dB时，含有环境噪声的声源信号干涉条纹与Radon变换后的列方差向量曲线。如图，由于环境噪声的影响，水面水下目标辐射噪声干涉条纹Radon变换后的列方差向量曲线峰值个数差异性减小：信噪比为0 dB时，水面和水下声源对应的峰值个数分别为2个和2个；信噪比为5 dB时，水面和水下声源对应的峰值个数分别为3个和2个；但在信噪比为10 dB时，水面和水下声源对应的峰值个数分别为4个和2个，对辨别结果影响较小。本文后续的仿真，暂不考虑环境噪声的影响。

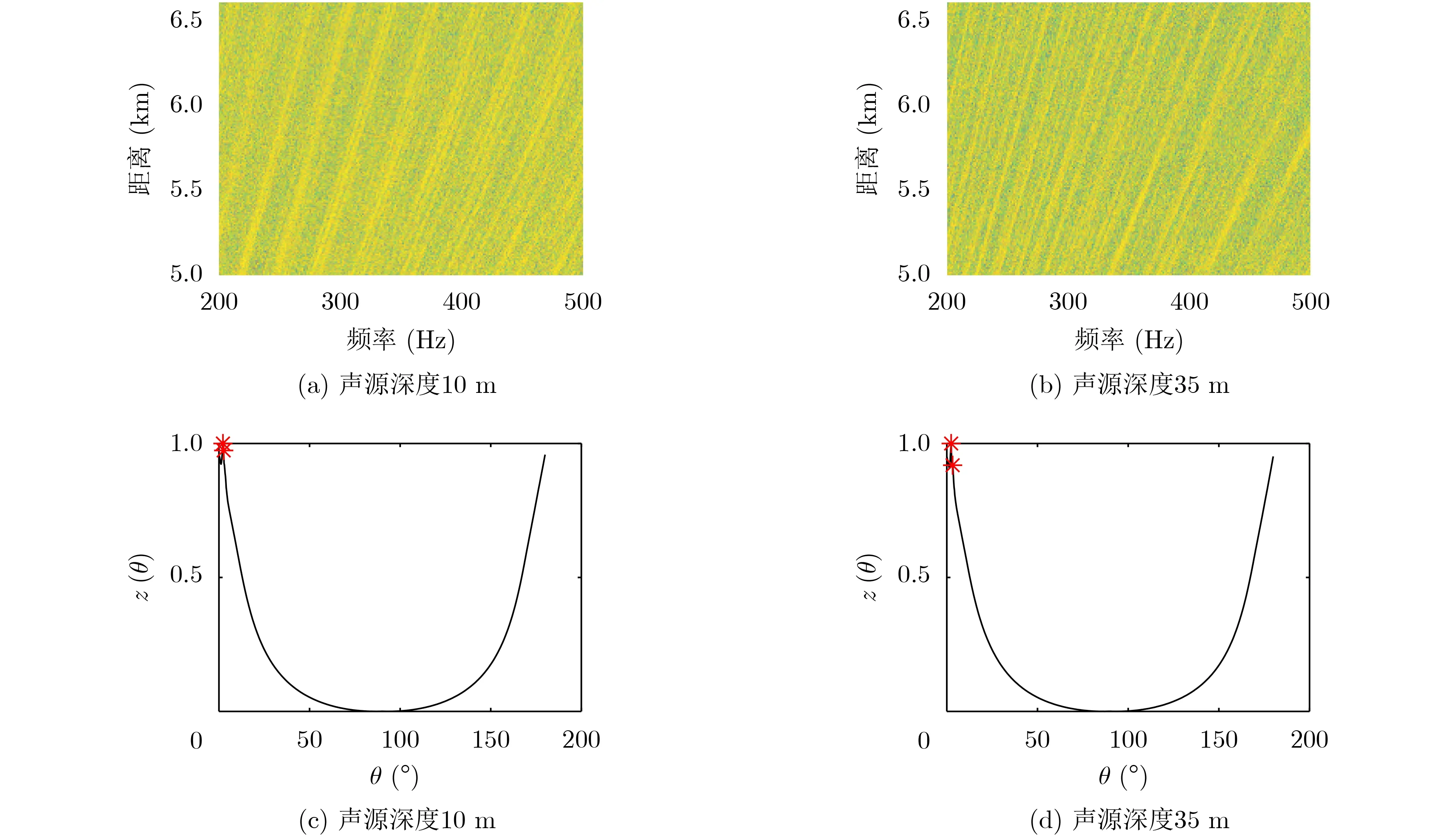
图8 信噪比为0 dB时辐射噪声干涉条纹图像及列方差向量曲线

图9 信噪比为5 dB时辐射噪声干涉条纹图像及列方差向量曲线

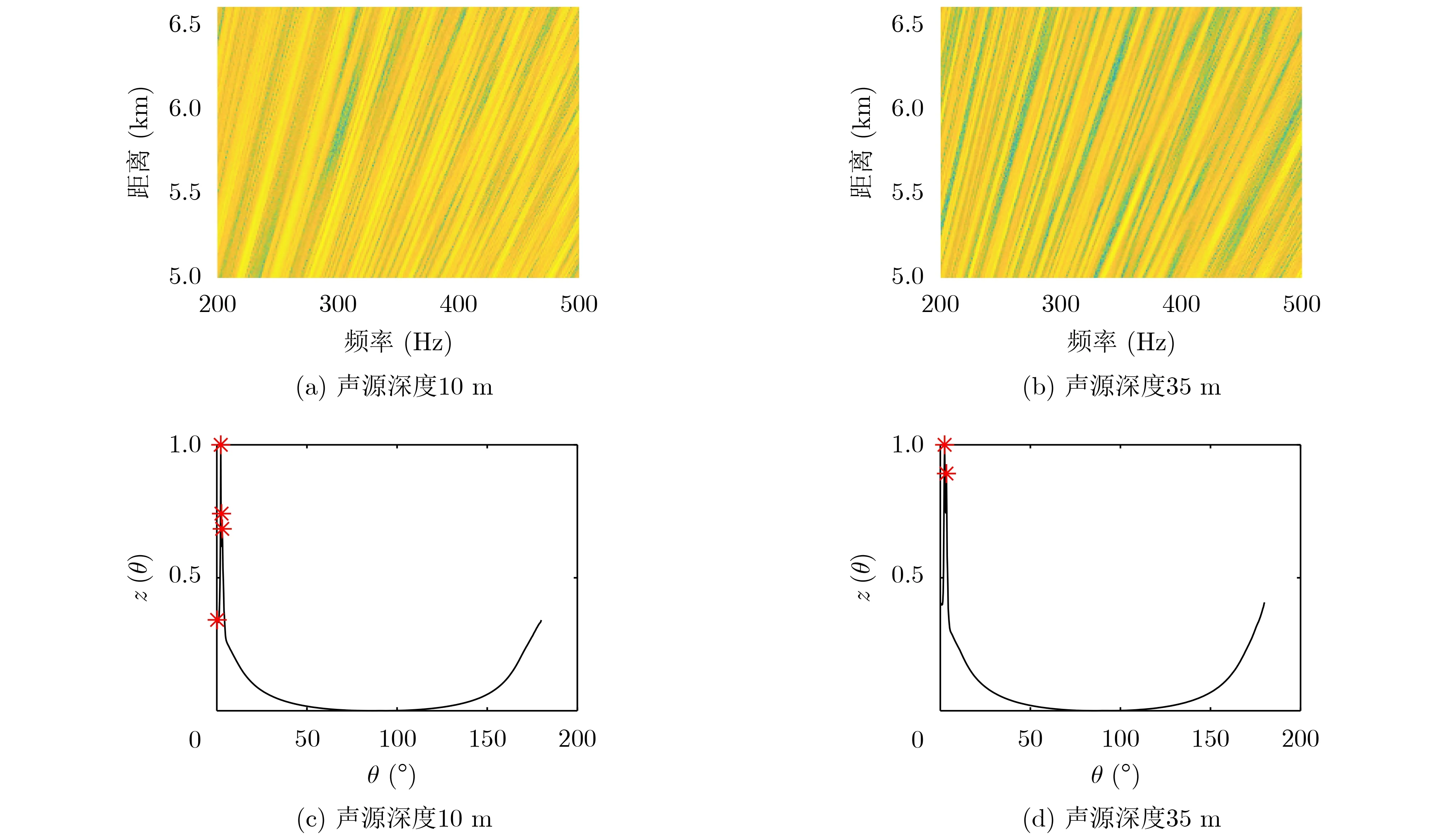
图10 信噪比为10 dB时辐射噪声干涉条纹图像及列方差向量曲线

以上分析可得水面水下目标判决的依据为：在分辨声源深度时，若目标的干涉条纹Radon变换矩阵的列方差向量峰值个数大于等于门限值时，判定声源为水面目标；若目标的干涉条纹Radon变换矩阵的列方差向量峰值个数小于门限值，判定声源为水下目标。根据前文的分析，在典型负跃层浅海环境中，门限值选取为3。

3 深度判别性能仿真分析

仍采用图1所示环境参数进行分析，选取信号频率范围200～500 Hz，频率分辨率1 Hz，距离范围5.0～6.6 km，距离采样间隔1 m，接收器深度选取13 m, 30 m, 35 m, 40 m和45 m，根据式(12)计算干涉条纹Radon变换矩阵的列方差向量并得到其峰值个数，仿真在这些接收器深度下的不同深度目标的分辨结果。定义深度15 m以上的声源为水面目标，深度为15 m及以下的声源为水下目标。图11给出了深度为5～80 m、深度间隔为1 m共76个不同深度的目标在5种不同深度的接收器下列方差向量的峰值个数，共380个仿真结果，其中纵坐标表示列方差向量的峰值个数为特定值时的水面或水下目标个数占水面或水下目标总数的比例。通过图11可知，水面目标的峰值个数较大，主要分布在3～4区间；水下目标的峰值个数较小，主要分布在1～2区间。方法具有一定可分性。

设定水面水下目标分辨门限值为3，得到5个不同深度接收器对不同深度声源的深度判别结果，若深度判别结果中判定为水面目标的接收器个数大于2个，认定目标为水面目标；反之，认定目标为水下目标，最终辨别结果如表2所示。

为了分析接收阵深度分布对方法性能的影响，现在与图12相同的水文环境下仿真不同接收深度覆盖范围的情况。图12给出了深度为5～80 m、深度间隔为1 m的76个目标在5个不同深度的接收器下，干涉条纹Radon变换矩阵的列方差向量峰值个数的总体分布，选取信号频率范围200～500 Hz，频率分辨率1 Hz，距离范围为5.0～6.6 km，距离采样间隔为1 m，横纵坐标的含义与图11相同，共760个仿真结果。图12(a)的接收深度主要覆盖范围在负跃层以上，其深度分别为15 m, 18 m, 20 m,22 m和25 m；图12(b)的接收深度主要覆盖范围在负跃层以下，其深度分别为30 m, 35 m, 40 m,45 m和50 m。由图12可得，方法在不同接收阵深度分布下仍能保持对水面、水下目标的分辨能力，但分辨能力在接收深度无法覆盖整体水层时下降。设定水面水下目标分辨门限值为3，最终目标辨别结果见表3和表4，计算方法与表2相同。

表2 目标深度分辨结果

表3 接收深度覆盖范围为负跃层以上的目标深度分辨结果

表4 接收深度覆盖范围为负跃层以下的目标深度分辨结果

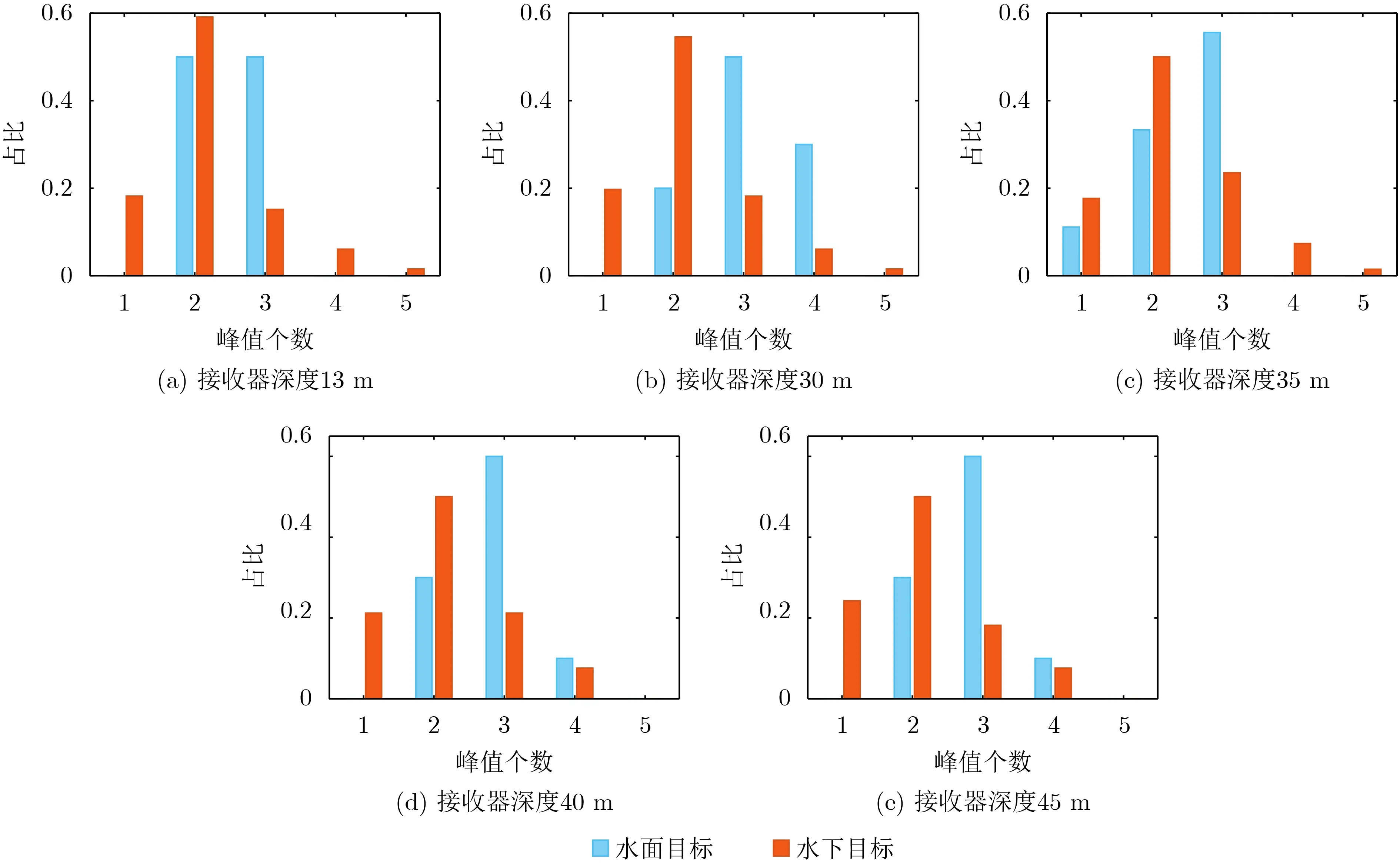
图11 不同接收器深度的峰值个数计数结果

图12 不同接收深度覆盖范围的峰值个数分布

为了验证方法对目标距离、信号频带的敏感性，现在与图11相同的水文环境下仿真不同频率范围和距离范围的情况。图13给出了深度为5～80 m、深度间隔为1 m的76个目标在5个不同深度的接收器下，干涉条纹Radon变换矩阵的列方差向量峰值个数的总体分布，信号的频率分辨率为1 Hz，横纵坐标的含义与图9相同，共760个仿真结果。图13(a)的信号频率为100～400 Hz，距离范围为5～6.6 km，接收器深度分别为13 m, 18 m, 25 m,40 m和50 m；图13(b)的信号频率范围为200～500 Hz，距离范围为9～10.6 km，接收器深度分别为13 m, 20 m, 30 m, 40 m和45 m。由图13可得，方法在不同频率、距离范围内仍能保持对水面、水下目标的分辨能力。设定水面水下目标分辨门限值为3，最终目标辨别结果如表5和表6所示，计算方法与表2相同。

表5 100～400 Hz频带范围的目标深度分辨结果

表6 9.0～10.6 km距离范围的目标深度分辨结果

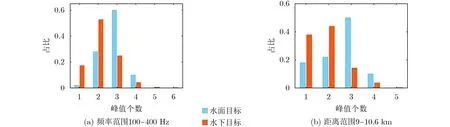
图13 不同频带、距离范围的峰值个数分布

仿真分析结果可知：在未知海洋声学环境参数的先验信息和声源距离时，方法对于水面水下目标有一定可分性，对目标距离、信号频带敏感性低，利用多个深度水听器进行综合判决且接收阵深度能覆盖整体水层的情况下准确率较高，有一定实用意义。

4 海试数据深度判别性能分析

利用2017年3月南海拖曳线列阵的试验数据对方法进行了验证，声速剖面如图14所示。试验海域水深为105 m，声源深度为20 m和8 m，数据处理的频率范围为200～300 Hz。在利用功率谱分析得到干涉条纹图像后，对图像进行低通滤波，并利用Radon变换检测滤波后的干涉条纹，最后计算干涉条纹图像Radon变换矩阵的列方差向量并判断其峰值个数，信号的具体处理流程见图15。

图14 南海声速剖面

选取不同声源深度、不同时间接收的4段辐射噪声信号，按图15所示流程处理后，得到辐射噪声信号的干涉条纹图像以及Radon变换矩阵的列方差向量，如图16和图17所示。图17(a)、图17(b)中，声源深度为8 m的两组信号中所得峰值个数分别为5个和4个，判定为水面目标；图17(c)、图17(d)中，声源深度为20 m的两组信号中所得峰值个数均为2个，判定为水下目标，与实际情况相符。与简正波分解、波导不变量、匹配场处理等传统被动定位方法相比，本文方法虽不能提供准确的声源深度估计值，但在存在负跃层的浅海波导条件下，可给出声源深度的二元判决，对目标类型的判别具有重要的支撑作用。该方法对声源距离和海洋环境声学参数等先验信息的依赖程度低，且无需求解简正波方差，计算量小，易于实现。

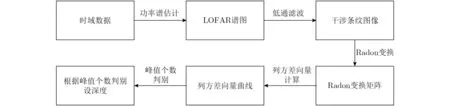
图15 深度判别处理流程图

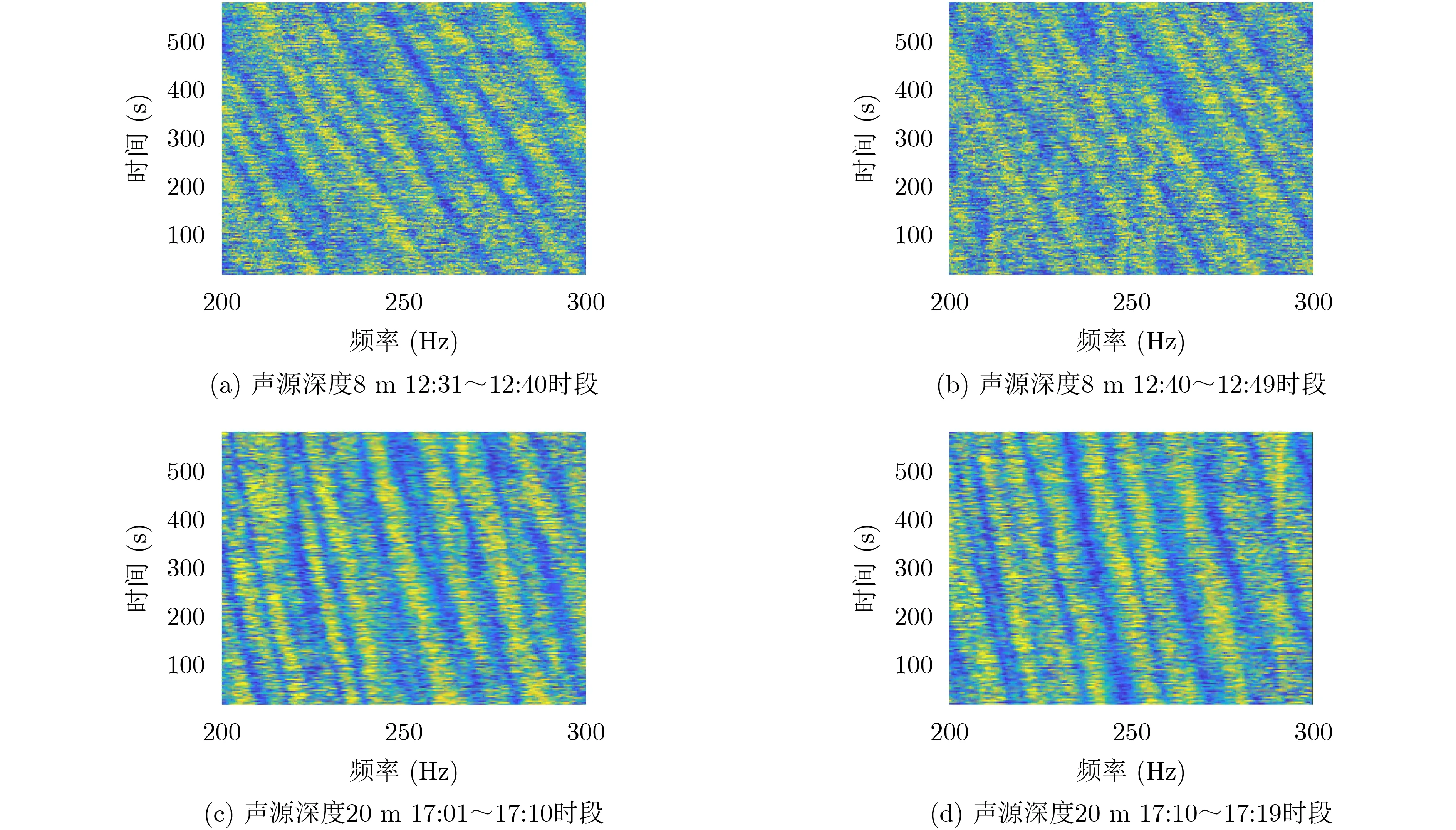
图16 实际数据的干涉条纹图像

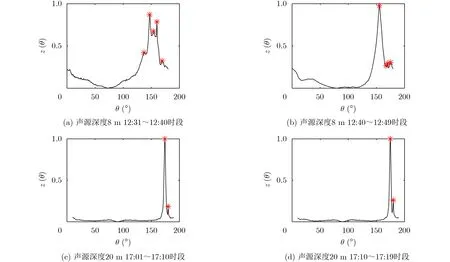
图17 实际数据的列方差向量曲线

5 结束语

辐射噪声干涉条纹的分布情况与水声环境和声源深度有较强相关关系。在夏季负跃层存在的水文环境中，水面声源激发的信号中高阶简正波占主导，水下声源激发的信号中低阶简正波占主导，这种差异性带来条纹斜率分布的差异性，可以根据干涉条纹斜率分布情况估计声源的深度区间。本文利用Radon变换对声场干涉条纹进行处理，得到以峰值个数为表征的干涉条纹斜率分布情况量化指标，进而分辨声源深度区间。海试数据处理结果表明，水面声源干涉条纹Radon变换后列方差向量的峰值个数较多，而水下声源干涉条纹Radon变换后列方差向量的峰值个数较少。相比于传统的匹配场、匹配简正波处理以及波导不变量方法，该方法不依赖声源距离和声速剖面的先验信息，既适用于阵列处理后的目标波束信号，也可用于单水听器接收信号，为水下目标分辨提供新思路。