浅海非高斯噪声下基于变分贝叶斯推断的波达角估计

冯 晓 周明章 张学波 叶 焜 王俊峰 孙海信

①(厦门大学信息学院 厦门 361005)

②(西北师范大学 兰州 730070)

③(天津理工大学集成电路科学与工程学院 天津 300384)

1 引言

波达角估计(Direction Of Arrival, DOA)是水下阵列信号处理[1-5]的关键技术。由于高斯噪声模型能够带来线性处理、由中心极限定理的理论支撑以及高斯噪声模型仅由均值和方差两个参数即可确定等3个方面的优势，传统大部分DOA估计方法是基于高斯噪声假设而实现的。在浅海环境中，海洋环境噪声受人工噪声、雷电噪声等影响严重[6-9]，表现出较强的非高斯特性，高概率出现的较大幅值使其概率分布具有重尾特性。在这种情况下，如果仍然使用基于高斯噪声的信号处理方法，将会极大地降低信号处理性能[10]。典型的海洋脉冲噪声模型通常用α稳态分布[11]与高斯混合分布(Gaussian Mixture Model, GMM)[12]来描述。对称α稳态分布(Symmetricα-Stable,SαS)由特征函数决定，其特征指数控制着分布的重尾程度。基于α稳定分布噪声的分数低阶矩特性(α<2)，文献[13,14]分别提出基于分数低阶矩的子空间方法，利用共变矩阵替代传统子空间方法中的方差即2阶矩特性，通过对分数低阶矩特性进行特征值分解，获得信号子空间。不同于前述算法中对于协方差矩阵的重构以及获得协方差矩阵的等效矩阵，文献[15]基于ℓp范数的子空间(ℓp-MUltiple SIgnal Classification,ℓp-MUSIC)算法利用残差拟合误差矩阵的ℓp范数最小化，通过解决产生的非凸优化问题直接获得信号子空间，然后构建MUSIC算法空间谱获得信号的DOA。然而基于ℓp范数最小化的问题是非凸优化问题，其算法性能取决于初始值的选择以及交替优化策略。针对SαS分布的水声信号，文献[16]提出一种0阶最小方差无畸变(Minimum Variance Distortionless Response, MVDR)波束形成器，在未知α参数值时，定义零阶阵列响应，其性能优于传统的MVDR波束形成器。基于 SαS分布噪声的分数低阶矩特性，文献[17]提出一种基于分数低阶相关-旋转因子不变的子空间(Fractional Order Correlation-Estimation of Signal Parameters via Rational Invariance Techniques, FOC-ESPRIT) 2维声源定位方法，利用矢量水听阵列的输出分数阶相关矩阵，结合子空间方法实现2维DOA估计。基于高斯混合噪声模型，文献[18]提出一种空间交替生成(Space Alternating Generalized EM, SAGE)算法，其递归搜索过程的初始值由MUSIC算法获得，通过2维搜索实现声矢量阵列3维声源定位。上述方法对接收信号协方差矩阵的受干扰程度较为敏感，其性能高度依赖快拍数以及信噪比，并且需要信号数量的先验信息。

稀疏表示方法广泛应用于阵列信号处理[19-22]，其中稀疏贝叶斯(Sparse Bayesian Learning, SBL)方法具有较小的信号重建误差[23]。在SBL框架内，高分辨DOA估计技术相继提出[24,25]。文献[26]提出针对水声环境的离网格(Off-Grid, OG) SBL估计方法，将离网格误差引入稀疏信号模型，实现相干水声信号DOA高分辨率估计。文献[27]提出在脉冲环境下基于SBL的DOA估计方法(IMPULSIVE SBL)，可以进行较好的DOA估计。变分贝叶斯推断(Variational Bayesian Inference, VBI)可实现对未知确定性参数分布的低复杂度估计[28]。文献[29]提出一种基于变分推断的鲁棒压缩感知(Robust Bayesian Compressed Sensing, RBCS)的脉冲噪声下的DOA估计方法，利用β-伯努利分布层次化先验对脉冲成分进行标识，并置零来消除脉冲噪声的影响，该算法存在对脉冲噪声的误定位问题。

在稀疏贝叶斯估计框架下，本文考虑浅海非高斯噪声的影响，提出一种基于变分贝叶斯推断的DOA估计方法。首先，利用信号角度信息和脉冲噪声的联合稀疏性，构建多测量向量稀疏信号恢复模型；其次，考虑脉冲噪声成分在不同快拍中的独立性以及信号成分的共稀疏特性，分别对其赋予高斯混合先验，构建层次贝叶斯估计框架；然后，利用变分贝叶斯推断方法获得联合稀疏向量的后验概率估计。将离网格误差引入稀疏信号模型，采用根稀疏贝叶斯方法进行离网格角度估计，进而实现离网格误差的校正，获得较为准确的估计性能；然后通过循环迭代获得DOA估计信息与离网格误差补偿信息，同时消除脉冲噪声影响；最后通过仿真实验验证本文算法的有效性。

2 信号系统模型

2.1 DOA估计模型

2.2 离网格DOA估计模型

3 基于变分贝叶斯的DOA估计

考虑多快拍信号构建多变量测量向量，将其转化为稀疏信号恢复问题模型为

3.1 稀疏贝叶斯估计框架

根据系统模型式(4)，接收信号的似然估计函数为[20]

3.2 变分贝叶斯DOA估计

3.3 离网格误差补偿

完成参数集ς的变分贝叶斯推断，如观测模型式(3)的描述，离格误差β尚未进行估计，当前的模型仍然存在离格误差。文献[31]提出根稀疏贝叶斯的离网格误差处理方法，将网格位置作为可调节参数，利用最大期望(Expectation Maximization,EM)算法递归精细化粗网格，更新的网格点通过多项式求根获得。本节主要研究β的更新，关于Φ(β)的负对数似然函数概率密度为

4 仿真实验与分析

4.1 脉冲噪声模型

4.2 空间谱估计

首先对不同算法的DOA估计的空间谱性能进行比较，快拍数T=100。针对基于贝叶斯估计的DOA估计算法，将估计向量的后验概率估计值进行功率归一化处理，然后与MUSIC 类型的算法的空间谱进行比较，如图1所示。图1(a)为GSNR=0 dB 时SαS噪 声下的空间谱估计结果。SαS噪声参数为α=1.4 ,γ=1。从中可以看到IMPULISVESBL具有最高的分辨率，然而其主峰位置偏离目标方位，产生低精度估计。与之相比，本文算法的主瓣宽于IMPULSIVE-SBL，但是本文方法的主峰位置更接近目标方位。此外，与其他对比算法相比本文方法具有更好的分辨率性能，具有较低的旁瓣性能。OGSBL算法空间谱最大峰值可以实现正确DOA估计，但是由于受到脉冲噪声影响严重，OGSBL对目标向量的后验估计的功率谱产生较多旁瓣，具有多个幅度较高的伪峰。RBCS的分辨率较低，其他MUSIC类型的算法的分辨率未达到本文算法的分辨率水平。

在GMM噪声环境下，空间谱对比如图1(b)所示。GMM 噪声参数为µ=0.1,κ=100, SNR=-5 dB。从中可以看出IMPULSIVE-SBL具有最优的分辨率，然而其-5.4°的主瓣估计偏离正确位置。除IMPULSIVE-SBL算法外，本文算法估计具有更优的空间分辨率，具有较窄等主瓣以及较低的旁瓣，在GMM噪声下体现出更高的抗干扰特性。RBCS的空间分辨率较差，主瓣较宽；OGSBL算法在GMM噪声下产生较多的估计伪峰，其在脉冲噪声下性能严重下降，不具有较好的抗脉冲干扰性能；ℓp-MUSIC算法的分辨率略差于本文算法，ROCMUSIC 和FLOM-MUSIC算法的空间谱估计具有明显的伪峰值。

图1 不同噪声下的空间谱估计

4.3 DOA估计性能比较

本文采用蒙特卡罗实验的DOA估计的均方根误差(Root Mean Square Error, RMSE)和精确度(Accuracy)和作为衡量指标，体现本文算法优势。RMSE是一种有效衡量DOA估计算法的性能指标，其定义为

仿真实验进行Mc=200次蒙特卡罗实验，快拍数T=300 ，分别在SαS噪声和GMM噪声下进行RMSE和Accuracy性能比较。在 SαS噪声下的DOA估计的RMSE和估计精度结果分别如图2(a)和图2(b)所示， SαS 噪 声参数为α= 1.5,γ= 1, GSNR=[0:2:20]。从中可以看出，本文算法获得最好的RMSE和估计精度性能。在低GSNR的情况下，由于较强的脉冲噪声的影响，本文算法具有明显的性能优势，随着GSNR的升高，脉冲噪声影响下降，RBCS算法估计性能逐渐接近本文算法，在GSNR＞15 dB时，由于RBCS算法未考虑离网格误差的影响，RMSE和精度的估计性能均下降。IMPULSIVE-SBL算法在GSNR=8 dB时可以接近本文算法性能，但在低GSNR时RMSE性能差于本文算法。在MUSIC类型算法中，三者之中最优的ℓp-MUSIC算法在整个GSNR范围内，其RMSE和精度估计均略差于本文算法。OGSBL算法在低GSN R 下具有一定的抗干扰能力，随着G S N R提高，由于其考虑网格误差的影响，在GSNR＞18 dB时，性能逐渐优于RBCS算法。

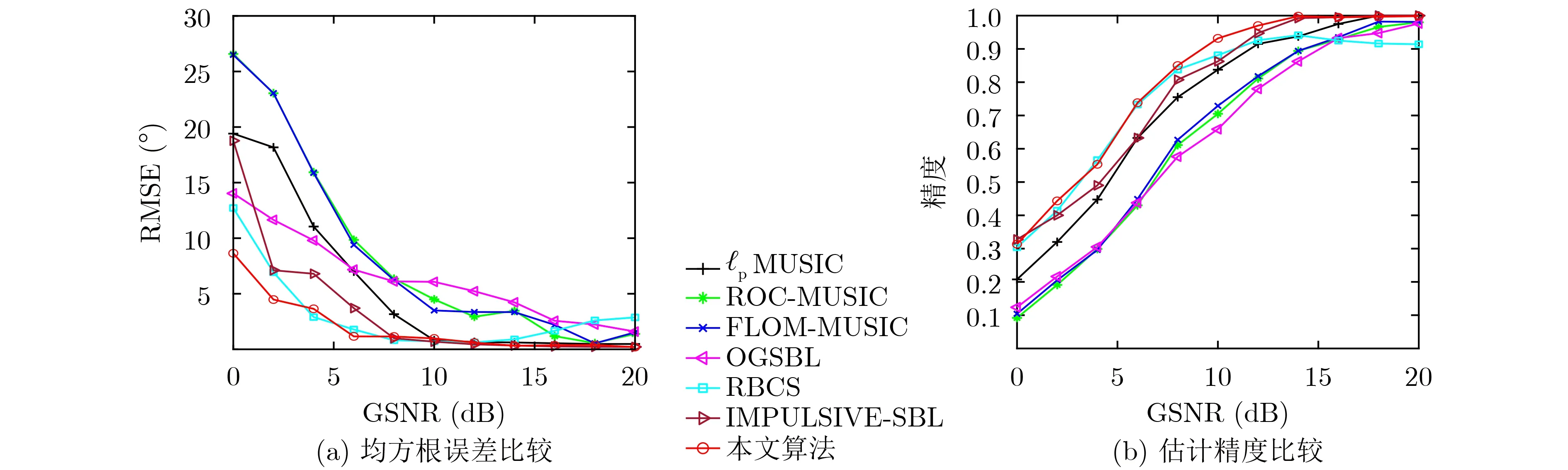
图2 不同GSNR下的DOA估计性能比较

图3为GMM噪声下DOA估计的RMSE和精度性能比较结果，GMM噪声参数µ= 0.1，方差之比κ= 100，SNR范围为[-4:2:16]。图3(a)为GMM噪声下不同SNR的DOA 估计RMSE性能比较，从中可以看出本文算法在整个SNR范围内具有最优的估计性能，特别是在低SNR情况下，本文算法估计性能优势大约在1个数量级，随着SNR的增加，估计性能之间的差异减小，本文算法仍保持性能优势。图3(b)中同样显示本文算法能够获得最优的精度估计性能。随着SNR的增加，MUSIC类型的估计算法对于信号共变协方差矩阵的估计准确度提高，在SNR＞4 dB时，DOA估计性能显著提升。对于OGSBL算法而言，由于信号功率的增加，脉冲噪声的影响减小，OGSBL算法性能在高SNR时接近本文算法。由于脉冲噪声模型与噪声参数选择之间的差异，RBCS算法在SNR＞0 dB时估计性能未获得明显提升，另外，由于RBCS缺少离网格误差的处理，其RMSE和精度性能差于ℓp-MUSIC，在SNR＞8 dB时差于OGSBL算法。在低SNR情况下，IMPULSIVE-SBL算法在-2 dB＜SNR＜2 dB的情况下，性能优于RBCS算法，本文算法与之相比仍具有一定的性能优势。综上两种噪声情况的比较，本文算法对于GMM脉冲噪声具有更强的鲁棒性。

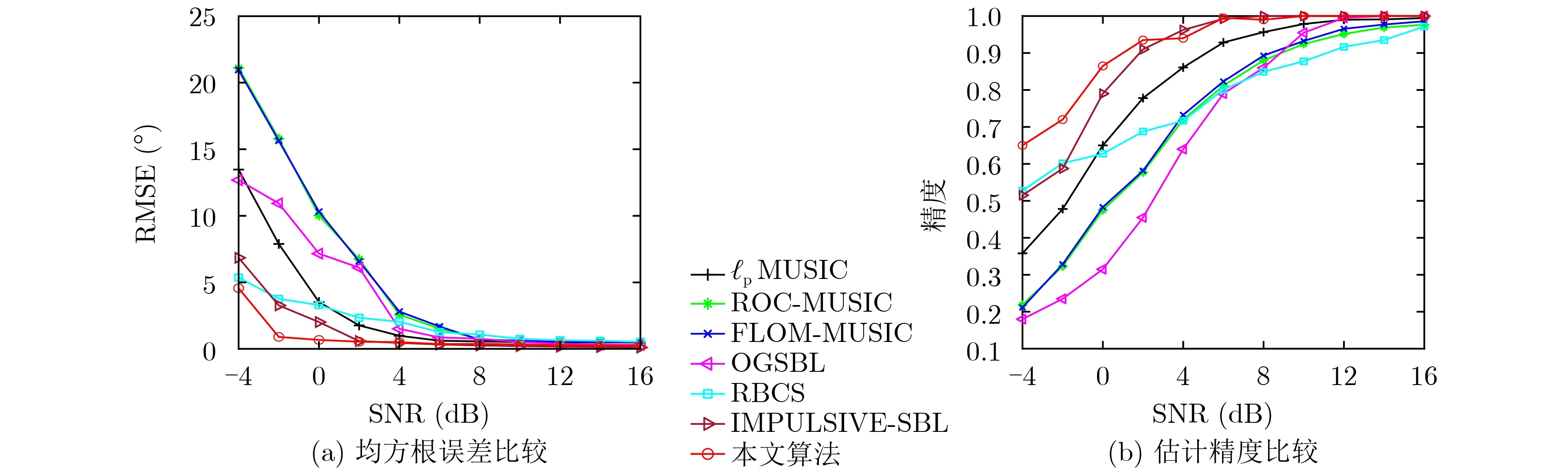
图3 不同SNR下的DOA估计性能比较

4.4 浅海噪声下DOA估计

在厦门五缘湾采集浅海环境噪声用于本文算法的性能验证。该测试海域水深约8 m，接收水听器位于离岸约20 m，水深4 m处。平均风速3级，脉冲噪声主要来源于水体搅动，以及过往船只的声音。信号采样率为153600 Hz，每次采集时间约为10 s，海洋噪声示例如图4所示。从噪声时域图中可知其具有明显的脉冲特性。选取其中6组海洋噪声数据样本，分别与 SαS噪声分布和GMM噪声分布进行参数拟合，结果如表1所示。表格中显示实际浅海噪声特征指数α ∈(1,2] ，γ在1左右；与GMM噪声拟合，其概率µ在0.1左右。取8段随机海洋噪声样本作为不同的阵元接收干扰信号。根据海洋实验环境噪声功率，在仿真环境中设置不同的信号发射功率，信噪比范围SNR=[0:2:20]，入射信号角度[-5.4°, 15.6°]，快拍数T= 1000。DOA估计RMSE性能如图5所示，从图中可以看出本文算法在整个SNR范围内估计性能最好，随着信号功率的增加，DOA估计精度逐渐提高。IMPULSIVESBL算法性能在实际噪声情况下，在设定的SNR范围内，性能接近本文算法。基于MUSIC的算法在低SNR时，在浅海噪声的影响下无法获得准确的DOA估计，OGSBL和RBCS在整个SNR范围内无法获得性能提升，估计RMSE保持在0.5°左右，对于浅海噪声具有较差的鲁棒性。

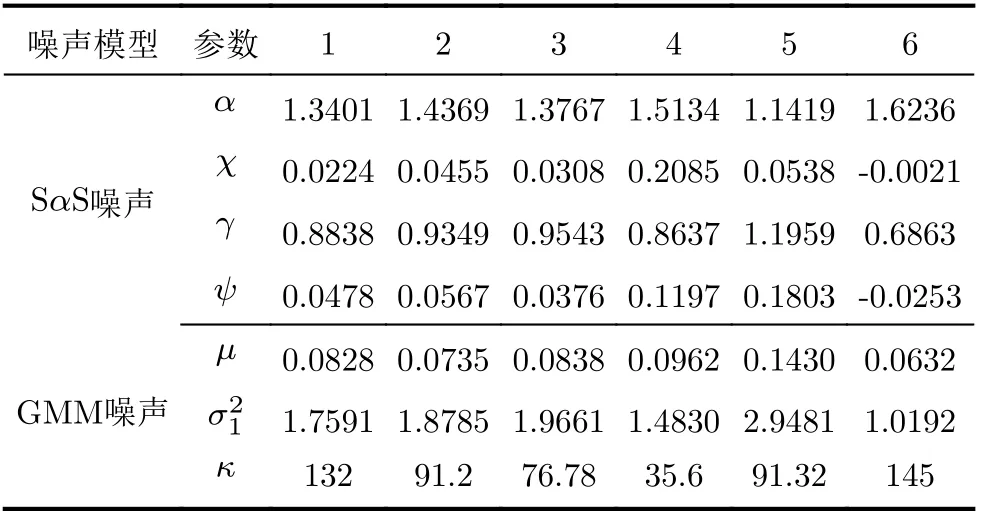
表1 浅海噪声参数拟合

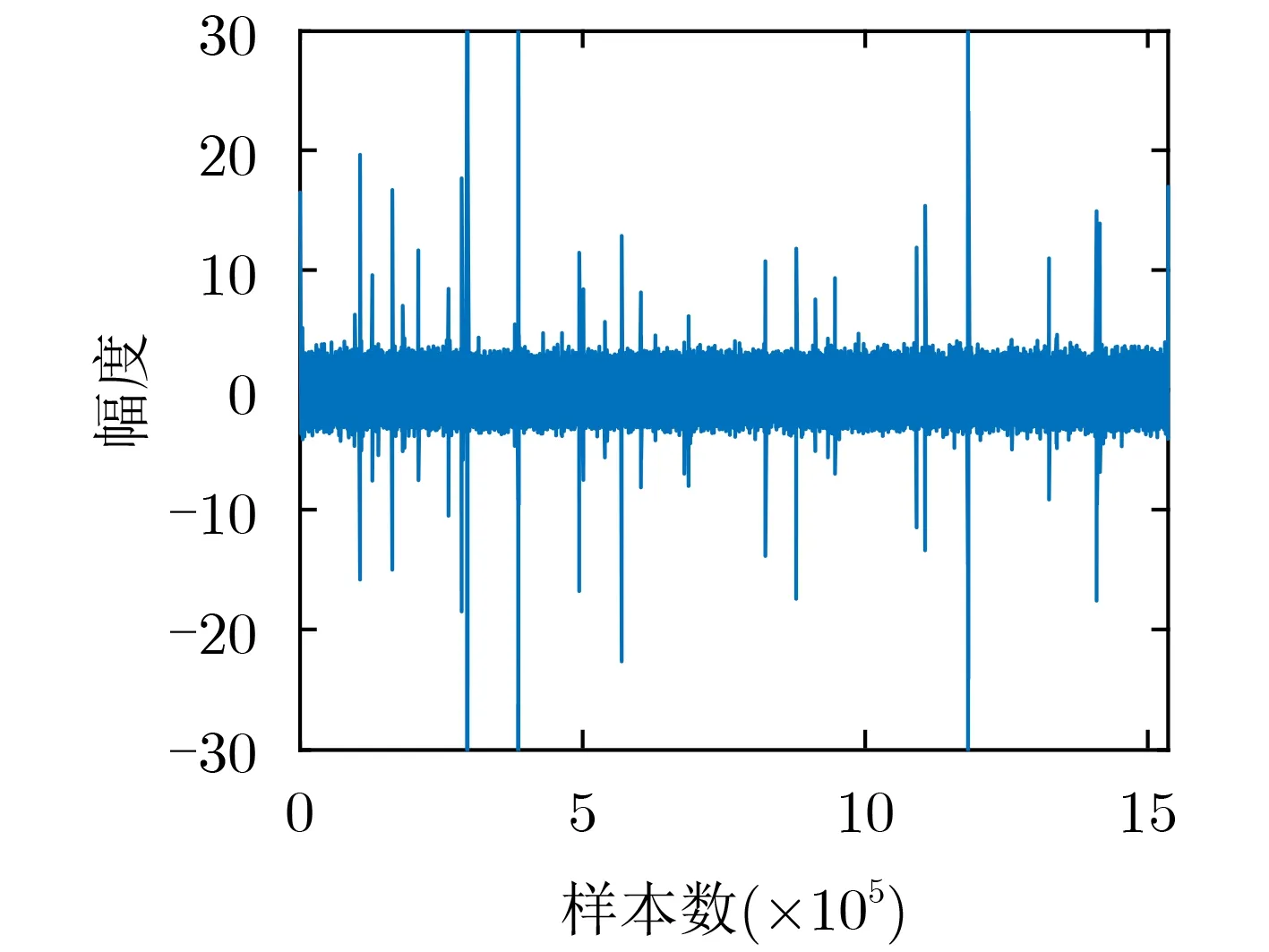
图4 浅海噪声样本示例

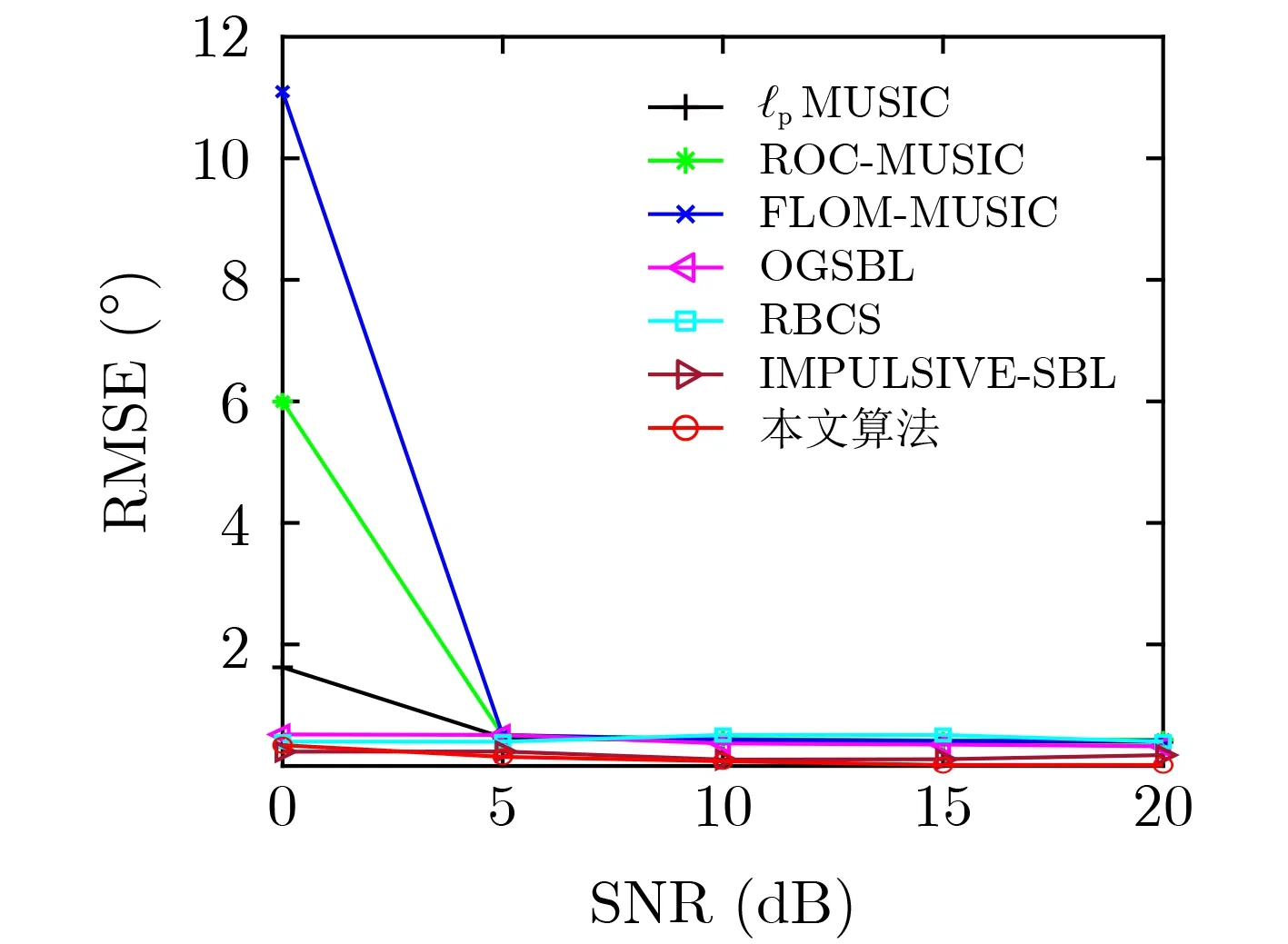
图5 浅海噪声下的仿真DOA估计RMSE

5 结束语

针对海洋脉冲噪声下的DOA估计性能下降的问题，本文提出一种基于变分贝叶斯推断的DOA估计方法。首先将信号与脉冲成分构成联合估计向量，利用多快拍数据构建多变量稀疏表示模型。考虑联合向量之间的信号成分的共稀疏特性和脉冲噪声之间的独立稀疏性，建立层次化稀疏贝叶斯估计框架，利用变分贝叶斯推断方法获得联合向量的近似后验概率估计。在稀疏表示模型中考虑离网格误差，采用根稀疏贝叶斯方法实现离网格误差信息估计。最后通过迭代更新获得最终的DOA估计与离网格信息补偿，同时消除脉冲噪声的影响。仿真实验结果表明，在典型脉冲噪声模型以及实测浅海噪声的影响下，本文算法比传统算法具有更好的估计性能，特别在低信噪比情况下，具有更高的分辨率和估计精度。对于不同脉冲噪声，本文算法比传统方法具有更好的鲁棒性和抗干扰特性。利用实测水声信号进行本文算法的DOA估计性能验证，是下一步的工作重点，同时开展强脉冲干扰或簇稀疏海洋环境噪声影响下的阵列信号处理技术相关研究。