出海水闸工程渗流特性计算分析研究

蔡超英

（上海市堤防泵闸建设运行中心，上海市 200080）

1 研究背景

水闸作为平原河网地区常见的水工建筑物，一般均具有防洪、挡潮、排涝及活水畅流等功能。由于水闸的主体建筑物一般均位于水下，水闸闸基在长期水流的渗流作用下，容易产生变形，导致水闸闸基失稳。出海水闸作为一线口门建筑物，往往内外河水位差较大，内外河水位变化较为频繁，渗流作用较为明显。长期的渗流作用可能引起流土或管涌现象，导致土体变形失稳。出海水闸闸基发生渗透破坏往往有2 个主要原因：水闸防渗体设计存在缺陷，特别是部分水闸防渗设计未充分考虑水闸侧向绕渗的影响，长期的渗透作用导致闸基发生渗透破坏；防渗体施工质量不佳，长期的渗流作用下，防渗体发生破坏。所以在出海水闸前期的设计中，采取科学有效的手段及方法对水闸渗流稳定进行精确计算是十分必要的。出海水闸的渗流计算一般采用改进阻力系数法，改进阻力系数法是在分段法、阻力系数法上发展而来的一种传统近似计算方法[1]。改进阻力系数法主要是首先明确边界条件，然后根据闸基及防渗体的几何形状对渗流场进行划分，利用现有的流体力学计算方法，计算出每段的阻力系数，从而计算出每段的渗透水头及渗透坡降[11]。但是改进阻力计算法还是一种近似算法，本文在改进阻力计算的基础上，利用三维有限元法对芦潮港水闸闸基渗流计算，并与改进阻力系数法的计算结果进行对比分析。此外对于水闸工程的侧向绕渗，由于侧向绕渗的渗流通道较多，流网较为复杂，很难对侧向绕渗进行精确计算，故传统方法对侧向绕渗的计算存在很大的模糊性及不确定性。故本文利用三维有限元软件，在侧向绕渗计算中，通过对等势线分布及渗流流速的分析，得出量化的结果，可以寻找出侧向绕渗最大渗透坡降的位置。

2 渗流的基本定律

2.1 渗流的基本定律—达西定律

本文对进行闸基渗流和侧向绕流分析，主要应用到达西定律，表达式如下：

式中：v 为渗透流速；Q 为渗透流量；A 为过水断面面积；L 为渗透路径长度；k 为多孔介质的渗透系数；J为渗透坡降；H1、H2为分别为上、下游过水断面的水头。式中的负号“-”表示水总是流向水头减小的方向。

2.2 渗流的基本方程

主要应用到几个基本方程：

（1）连续性方程

连续性方程的实质是质量守恒方程，根据质量守恒原理来考虑可压缩土体的连续性规律，在渗流场中，地下水在任意一个单元体内的速率变化差等于进入该单元体内的流量速率之差。

根据质量守恒定律，水在渗流场流动过程中，可以简单的认为渗流连续性方程的质量是既不增加也不减少的。

如果把土和水作为弹性体而考虑压缩性时，引入土体压缩系数α、水体压缩系数β。经过推导后得到可压缩土体中渗流的连续性方程：

当流体密度为常数且多孔介质不可压缩时，该方程简化为：

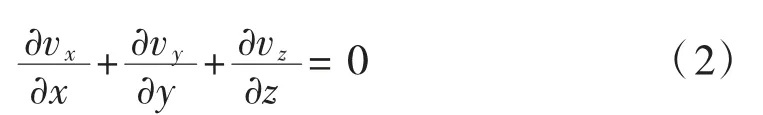
（2）稳定渗流微分方程

对于水头h 不随时间改变的稳定渗流，根据达西定律，将x、y、z 方向的渗流速度表示为：

将式（3）代入式（2），得到稳定渗流的微分方程式：

（3）非稳定渗流微分方程

对于水头随时间改变的非稳定渗流，把式（3）代入式（1），得到：

式（5）即考虑了土体和水体的压缩性的非稳定渗流微分方程。

式中：h 为总水头；kx、ky、kz为分别为X、Y、Z 方向上的渗透系数；S 为单位体积的饱和土体。

3 渗流的有限元分析原理

采用Galerkin 逼近方法，将全部计算区域离散成互不重叠交叉的有限单元[2]，结点总数为NP，单元总数为NE，设

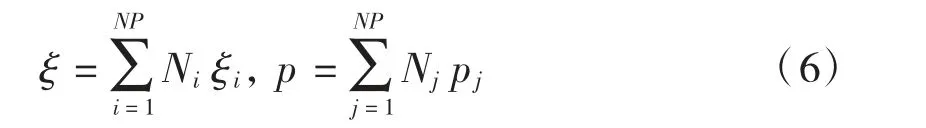
式中：Ni，Nj为结点形函数。代入并考虑到是任意函数，其每一个系数都应等于零，则得

式中：Na，Nb为单元结点局部形函数；Ωe为单元区域。

式（7）可简写为如下有限元矩阵方程

式中：

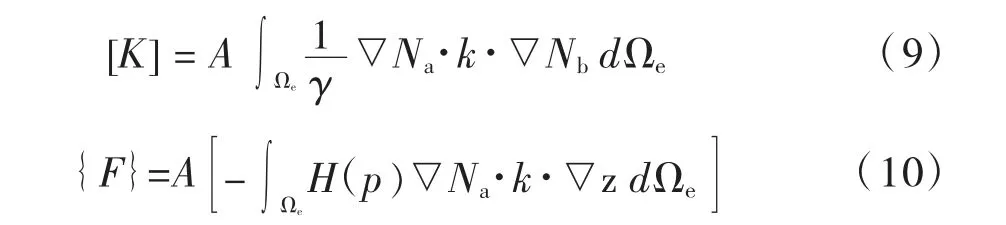
式中：A 为组合算子，它把各个单元的结点贡献累加到总体渗透矩阵和结点荷载列向量中去。式（8）是非线性的，可用截止负压法求解[10]。

采用负的罚参数ε，并定义罚函数Hε（p）如下

其中ε 为罚参数，可由式（12）计算

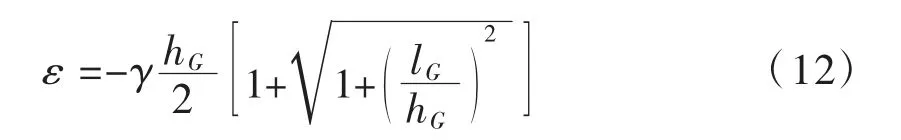
式中：lG，hG为单元结点到离它最近的积分点的水平和垂直的距离。显然，当网格→0 时，ε→0。由此，可以构造如下迭代格式来求解式（8）。

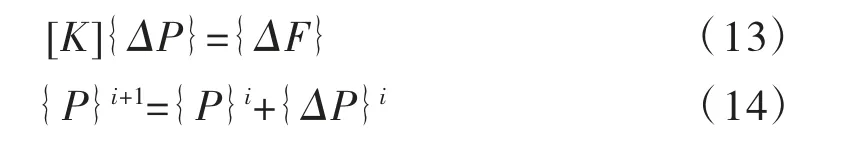
式中：i 为迭代次数；｛ΔP｝为压力函数修正量；｛ΔF｝为结点不平衡荷载向量，由式（15）计算

采用八结点六面体等参数单元，见图1，按迭代格式，式（13）、式（14），可求得渗流的压力场，并由此计算位势场、自由面坐标、渗透坡降、渗透流速等各种所需的物理量[10]。

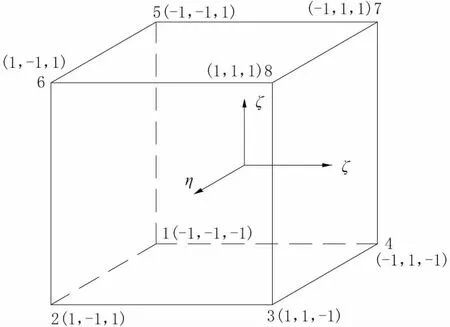
图1 三维参数母单元

4 实例分析

4.1 工程概况

芦潮港水闸地处上海市浦东新区南汇新城，为芦潮港入杭州湾的一线口门水闸，靠近长江口和杭州湾的交汇处，其功能集防洪、挡潮、排涝及活水畅流等功能于一体，是临港新城沿杭州湾的重要口门水闸之一。

芦潮港水闸闸首采用整底板框架式结构，并设3孔，每孔设两道闸门，互为备用。闸门底坎高程-1.50 m，外门顶高程4.50 m，上设胸墙，内门顶高程6.00 m。芦潮港水闸闸首为一联三孔布置，总净宽36.0 m。闸首顺水流方向长25.0，垂直方向长41.6 m。闸首底板厚2.00 m，底板顶高程-1.50 m。闸首墩墙顶高程9.70 m，闸首边墩宽1.3 m，闸首中墩宽1.5 m，水闸设次墙与两侧外河大堤防浪墙相连接。刺墙顶高程9.4 m，底高程约1.50 m，墙厚0.8 m，长16.85 m，刺墙下设3φ850@600 三轴搅拌桩作为防渗透。

芦潮港水闸为杭州湾出海水闸，地质条件较为复杂。其主体结构坐落于②3层灰色黏质粉土上，其主要新沉积欠固结土，渗透性较大。在上世纪六十年代，现有芦潮港水闸的前身，发生过因防渗破坏而沉没海底事故。可见芦潮港水闸工程对于工程的防渗措施有着较高的要求。

4.2 地质资料

从本工程水闸结构设计和地质勘察报告分析可知，整个水闸将座落于②3层灰色黏质粉土上，该层土特性松散～稍密，中等压缩性，土层物理力学性质尚可，但该层土表面为新沉积滩地土，土性指标存在着不稳定的因素。其渗透性较大（Kv=5.17×10-7cm/s，KH=7.83×10-7cm/s），地基存在渗透稳定的问题，需采取相应的防渗处理措施。并且根据本工程的抗震级别对②3层进行液化判别，地基的液化等级为轻微液化，在地基处理中也应考虑采取相应的措施，防止对水闸的主体部分产生安全隐患。②3层土下卧层为第⑤1-1层灰色黏土和第⑤1-2层灰色粉质黏土，土体呈流塑～软塑状，高压缩性，土质较差，该两层土为水闸地基产生沉降主要的压缩土层。第⑥层暗绿～草黄色粉质黏土、第⑦1层草黄色砂质粉土和第⑦2层灰黄色粉砂土性指标较好，均可作为水闸闸首的桩基持力层。具体参数见表1。

表1 土层主要物理力学性质参数表

4.3 闸基渗流

（1）计算模型

该闸的地下轮廓线见图2。

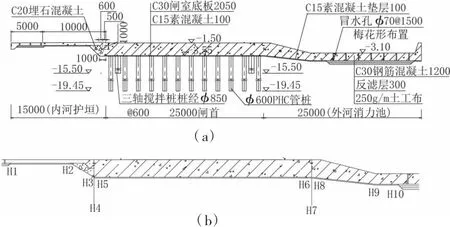
图2 地下轮廓线（单位：mm）

计算模型见图3。

图3 计算模型

地基土体的单元类型采用CPE4P，闸底板等混凝土结构采用CPS4R 类型的单元即不考虑它的透水性。根据计算经验，地基土顺水流方向长度取水闸地下轮廓线顺水流方向投影长度的三倍，132 m；竖直方向长度取地下轮廓线横竖直方向投影长度的2倍，28 m。

（2）计算工况

本文以芦潮港内外河最大水位差作为特征水位组合进行计算，见表2。

表2 水位组合

（3）计算结果分析（见图4～图7）

图4 正向工况孔压分布

图5 反向工况孔压分布

图7 反向工况流速矢分布

图6 正向工况流速矢分布

正向工况的水位差最大，所以这里将用改进阻力系数法计算和有限元法计算两排桩、单排桩、无桩情况下的地下轮廓线各点渗透水头画在图8 中。

图8 渗透水头分布

利用达西定律进行计算出口渗透坡降。从云图分布图中可以看出在渗流出口处渗透坡降最大。

出口处的渗透坡降计算结果见表3。

表3 渗透坡降计算

根据计算结果可知，有限元法模拟了两排桩、单排桩、无桩情况下的地下轮廓线各点渗透水头变化情况。可知有桩时的渗透坡降比无桩时的坡降明显降低，防渗桩排数越多渗透水头的降低越明显。改进阻力系数法和有限元法对两排桩渗透情况进行比较发现，采用改进阻力系数法计算时在两排桩处渗透水头下降值较有限元法更大，截渗作用更加明显。说明传统改进阻力系数法计算偏保守。

4.4 侧向绕渗

（1）计算模型

根据试算，地基顺水流长度取180.0 m，垂直水流方向宽度取182.0 m，深度取30.0 m 可以完整包含侧向绕流的影响范围。这里不透水的部位均只保留边界，不反应实体，地基土体的单元类型采用C3D8P。将模型作适当的简化，侧向绕流计算模型见图9。

图9 侧向绕流计算模型

（2）计算结果分析（见图10～图15）

图10 正向工况浸润面

图11 反向工况浸润面

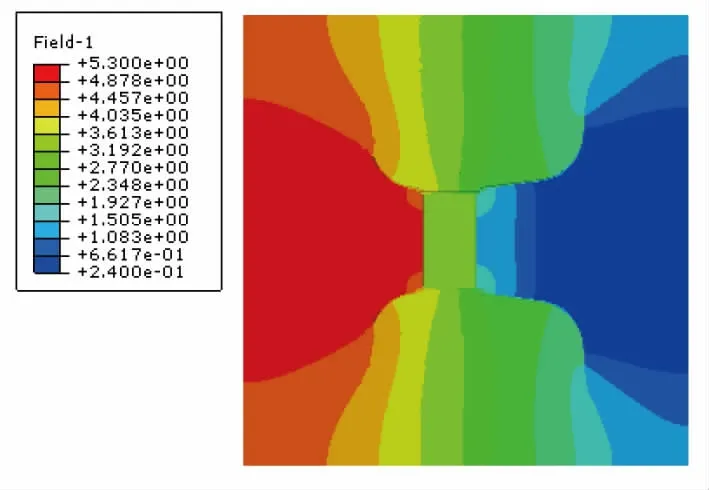
图12 正向工况等势线分布

图13 反向工况等势线分布

图14 正向工况流速矢分布

图15 反向工况流速矢分布

正、反向工况墙后水深见图16 和图17。渗透坡降计算见表4。

表4 渗透坡降计算

图17 反向工况墙后水位

通过三维有限元对侧向绕渗进行了计算，根据计算结果可知，侧向绕流的最大渗透坡降位于岸坡内，工程设置防渗桩后，渗透水头明显降低，渗透坡降满足相关规范的要求。可见防渗桩的设置对侧向绕渗起到了很好的抑制效果。

5 结 论

（1）根据闸基渗流计算结果可知，在布置防渗桩后，渗透坡降比无桩时的坡降明显降低。根据侧向绕流计算结果可知，侧向绕流的最大渗透坡降位于岸坡内，工程设置防渗桩后，渗透坡降明显降低，可见防渗桩设置起到了明显的截渗效果。

（2）同种工况下改进阻力系数法和有限元法进行计算比较发现，采用改进阻力系数法计算时在防渗桩处渗透水头下降值较有限元法更大，截渗作用更加明显。说明传统改进阻力系数法计算较有限元法计算更加保守。

（3）对于水闸工程的侧向绕渗，由于侧向绕渗的渗流通道较多，流网较为复杂，改进阻力系数法无法对侧向绕渗进行精确计算。本文利用三维有限元软件，在侧向绕渗计算中，通过对等势线分布及渗流流速的分析，得出量化的结果，可以寻找出侧向绕渗最大渗透坡降的位置。

（4）三维有限元法计算结果准确、直观，面对复杂地质条件及复杂的基础结构，传统解析法无法解决的问题，有限元法可以便捷地作出解答。传统的改进阻力系数法虽然计算偏保守局限性加大，但其具有一定的便捷性，在水利工程渗流计算中应用较为广泛。笔者认为三维有限元法对于传统计算方法来说不是一种替代，而是一种更好的补充。