CONTROL STRATEGIES FOR A TUMOR-IMMUNE SYSTEM WITH IMPULSIVE DRUG DELIVERY UNDER A RANDOM ENVIRONMENT*

Mingzhan HUANG (黄明湛) Shouzong LIU (刘守宗) Xinyu SONG (宋新宇)

College of Mathematics and Statistics，Xinyang Normal University，Xinyang 464000，China

E-mail:huangmingzhan@163.com;liushouzong@163.com;xysong88@163.com

Xiufen ZOU (邹秀芬)

School of Mathematics and Statistics，Computational Science Hubei Key Laboratory，Wuhan University，Wuhan 430072，China

E-mail:xfzou@whu.edu.cn

Abstract This paper mainly studies the stochastic character of tumor growth in the presence of immune response and periodically pulsed chemotherapy.First，a stochastic impulsive model describing the interaction and competition among normal cells，tumor cells and immune cells under periodically pulsed chemotherapy is established.Then，sufficient conditions for the extinction，non-persistence in the mean，weak and strong persistence in the mean of tumor cells are obtained.Finally，numerical simulations are performed which not only verify the theoretical results derived but also reveal some specific features.The results show that the growth trend of tumor cells is significantly affected by the intensity of noise and the frequency and dose of drug deliveries.In clinical practice，doctors can reduce the randomness of the environment and increase the intensity of drug input to inhibit the proliferation and growth of tumor cells.

Key words Tumor-immune system;chemotherapy;stochastic impulsive model;extinction;persistence

1 Introduction

Cancer is considered to be one of the most significant causes of human death in the world[1].It includes many kinds of diseases that are characterized by dysplastic cells which can divide uncontrollably and penetrate and destroy normal body tissue.In 2018，cancer caused more than 9.6 million deaths and another 18.1 million people were newly diagnosed with cancer[2].According to a report by the WHO in 2016，malignant tumors are one of the top two causes of death in 91 countries for people under the age of 70[3].In recent years，due to the improvement of cancer screening and treatment，the survival rate for many kinds of cancer is increasing.However，the occurrence of cancer has also been increasing due to population growth and aging and the increasing prevalence of risk factors such as smoking，obesity，lack of physical activity，and changes in reproductive patterns related to urbanization and economic development[4].

There is a complex interaction between the immune system and tumor growth.When the immune system detects the occurrence of a tumor，it can coordinate and promote the division of immune cells.Antibodies are produced and secreted into the blood or on the surface of the tumor by B-lymphocytes，while the antigens are destroyed by the effector cells (Cytotoxic-TLymphocytes，CTLs).This leads to the secretion of interleukins by T helper lymphocytes which can stimulate the division of both T and B cells.Then，T-suppressor cells terminate the immune response.The immune response process of tumors seems to be perfect.The immune system does not always work and tumors also process rigorous defense systems that can interrupt the occurrence of a fully efficient response[5].Thus cancer treatment is necessary.Cancer treatment may include chemotherapy，radiation，and/or surgery，and many factors influence the effectiveness of treatment.Chemotherapy is a widely accepted treatment that may cure some non-metastatic tumors and may even extend the lives of people with advanced cancer to some extent[6].

There is a long history of the study of tumor-immune dynamics，and a large number of mathematical models have been constructed.Most of the models are deterministic ones，and some of this research has focused on parameter estimates and the dynamic behavior analysis of the systems (see[7–21])，while other research has investigated the optimal control of cancer treatment (see[22–27]).These studies show that mathematical models can explain various characteristics of tumor growth and the regulatory function of the immune system，and the dynamical results are mostly based on the attractor study and bifurcation analysis of the corresponding mathematical models[19].In addition，based on the fact that tumor growth and the immune system are often perturbed by stochastic factors in the environment，several researchers have proposed stochastic models (see[6，28–34]and references therein).The authors in[6]studied the dynamics of tumor-immune responses under chemotherapy by a stochastic differential equations model and a continuous-time Markov chain model.The authors in[28]constructed a stochastic model to simulate the spontaneous regression and progression of a malignant tumor and studied its stochastic stability properties.Albano and Giorno in[29]investigated the solid tumor growth by a stochastic model，and studied the effects of a timedependent therapy by a numerical approach.Bose and Trimper in[30]studied tumor cell growth by formulating a stochastic model with both multiplicative and additive colored noises.Xu et al.in[31]explored the bifurcation phenomenon for a stochastic tumor-immune system with a symmetric non-Gaussian L´evy noise.Kim et al.in[32]compared the deterministic and stochastic models of cancer-virus dynamics，and investigated the parameter sensitivities.Deng and Liu in[33]obtained the permanence and extinction thresholds for tumor growth via a stochastic hybrid model，while Bashkirtseva et al.in[34]investigated the effect of random disturbances on the corporate dynamics of immune and tumor cells.

As a general rule，chemotherapy can be given in pill form or directly delivered into veins by injection or an IV.However，in any case，the delivery process is finished in a relatively short time，and then the drug begins to kill all kinds of cells and its lethality declines as it degrades.The drug delivery should always be performed many times in the course of chemotherapy.Thus it would be most appropriate to describe this behavior in terms of impulse perturbations.There are many studies on the effect of human pulse interference in disease control[35–43].For example，G.P.Samanta considered a competitive model to describe the interactions among tumors，normal and immune cells，and the additional effects of periodic pulse chemotherapy[35].

Motivated by the works mentioned above，this work attempts to explore the stochastically permanent extinction of tumor cells for the tumor-immune system responses to impulsive drug deliveries.A stochastic impulsive model for the tumor-immune responses to chemotherapy is formulated in Section 2.Then，in Section 3，we give several definitions and notations and carry out the survival analysis for tumor cells.Sufficient conditions for extinction，non-persistence in the mean，weak persistence and stochastic permanence in the mean are established.Then，numerical simulations are performed in Section 4 to illustrate the theorems obtained in Section 3，and also to reveal some specific features for the treatment of cancer.Finally，a brief conclusion is presented in Section 5.

2 Model Formulation

The ODE mathematical model proposed by Pillis and Radunskaya in[8]is as follows:

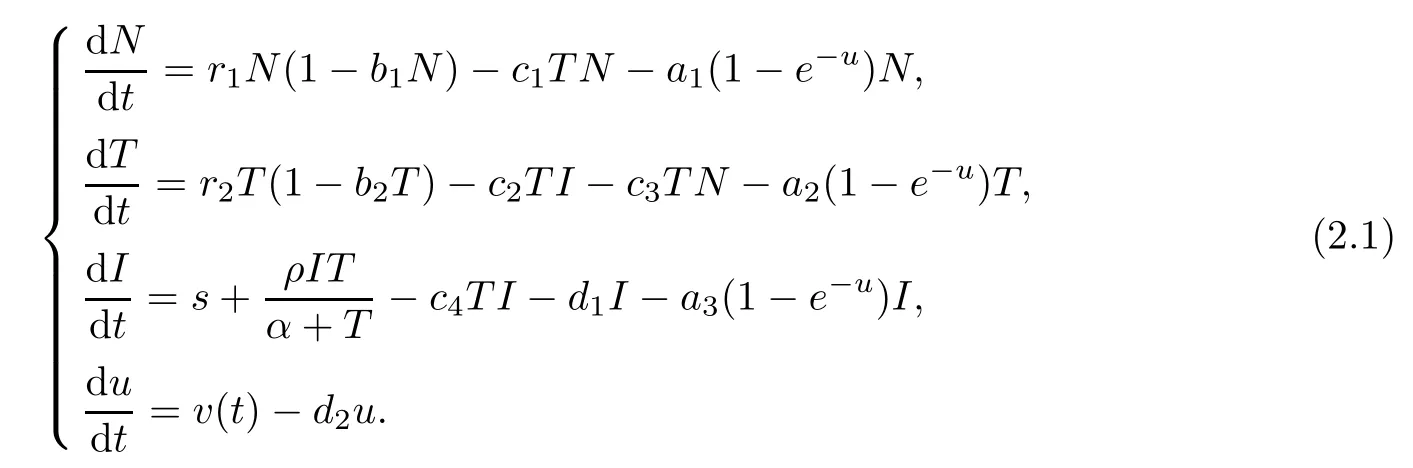
The state variablesN(t)，T(t) andI(t) represent the number of normal cells，tumor cells and immune cells at timet，respectively.u(t) is the amount of drug at the tumor site at timet.riandbi(i=1，2) stand for the per capita growth rates and reciprocal carrying capacities of the normal cells and tumor cells，respectively.These two types of cells are supposed to compete for available resources，andc1，c3are competition coefficients.sis a constant in flux rate of the immune cells，is the positive nonlinear growth of immune cells stimulated by the presence of tumor cells，andd1is the death rate.In addition，the immune response can result in either the death of tumor cells or the inactivation of the immune cells，thusc2andc4denote the corresponding interaction coefficients.v(t) is the delivery rate of a drug in chemotherapy.It is assumed that all types of cells can be killed by the drug，and the killing rates are different among cells with an exponential form

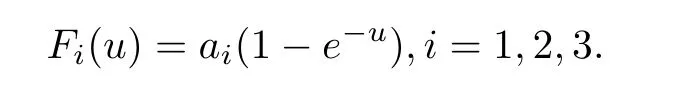
A time-varying drug termu(t)=u0e-d2thas been studied in[8]and this study implied that the solutions of the system with a drug approach the solutions of the system without the drug once treatment has stopped.In this paper，we are interested in periodically pulsed deliveries of a drug in a random perturbation environment.The external delivery of a drug is modeled by the Dirac Delta function.In addition，instead of altering particular parameters，we add a randomly fluctuating driving force directly to the above deterministic model (2.1).Then the resulting stochastic impulsive system is

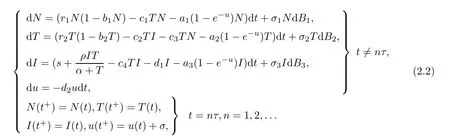
with initial valueN(0)＞0，T(0)＞0，I(0)＞0 andu(0)=0，whereσi，i=1，2，3 are constants representing the intensities of stochasticity and (B1，B2，B3) is a three-dimensional Wiener process.Furthermore，τis the period of drug delivery andσis the dose of drug input each time.

In this work，we provide a survival analysis of tumor cells for system (2.2)，and establish sufficient conditions for the extinction，non-persistence in the mean，weak persistence and stochastic permanence in the mean for tumor cells.

3 Main Results

For the sake of convenience，the following notations and definitions are assumed throughout the paper:

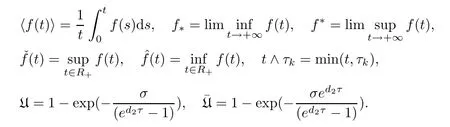
To study the survival and extinction of tumor cells，we firstly provide some definitions about persistence and extinction as follows:

(i) The tumor cellsT(t) in system (2.2) are said to go to extinction ifa.s.;

(ii) The tumor cellsT(t) in system (2.2) are said to have non-persistence in the mean if

(iii) The tumor cellsT(t) in system (2.2) are said to have weak persistence in the mean if〈T(t)〉*＞0;

(iv) The tumor cellsT(t) in system (2.2) are said to have strong persistence in the mean if〈T(t)〉*＞0;

(v) The tumor cellsT(t) in system (2.2) are said to have stochastic permanence if for any∈＞0，there are constantsβ＞0，M＞0 such thatP*{T(t)≥β}≥1-∈andP*{T(t)≤M}≥1-∈.

Remark 3.1In the above，we use the concepts of weak persistence in the mean[44]and strong persistence in the mean[45].

To begin with，we give some basic properties of the following subsystem of (2.2):

Lemma 3.2System (3.1) has a unique positive periodic solution¯u(t) with periodτ，where

The existence of a global positive solution of system (2.2) is first investigated.

Lemma 3.3For system (2.2)，there is a unique global solutionx(t)=(N(t)，T(t)，I(t)，u(t)) ont≥0 with any given initial valueN(0)＞0，T(0)＞0，I(0)＞0，u(0)=0，and the solution will remain inwith a probability of one.

ProofWe complete the proof of this conclusion in two steps.

Step 1We first consider the following stochastic model for tumor-immune responses to chemotherapy:

Obviously，{τk}is a monotone increasing sequence ask→∞.Settingthenτ∞≤τea.s..To show thatτe=∞，we only need to prove thatτ∞=∞.Ifτ∞＜∞，then there must exist a constantM＞0 andε∈(0，1) such thatP{τ∞＜M}＞ε.Thus，there exists an integerk1≥k0such that

Define aC2-functionby

The nonnegativity the functionVis obvious，sincey+1-lny≥0 ony＞0.Then，by It’s formula，one can see that

Taking the expectation on both sides of the above inequality，we can obtain that

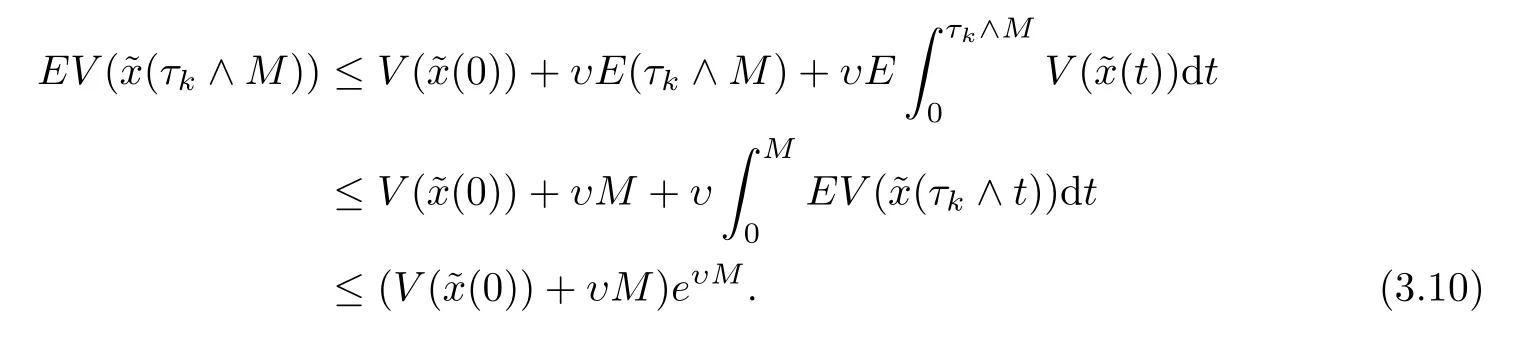
Set Ωk={τk≤M}，k≥k1.According to (3.4)，we have thatP{Ωk}≥ε.Note that for everyω∈Ωk，there is at least one ofthat equals eitherkor 1/k，henceV((τk，ω) is no less than (k+1-lnk)∧(1/k+1+lnk).

It then follows from (3.10) that

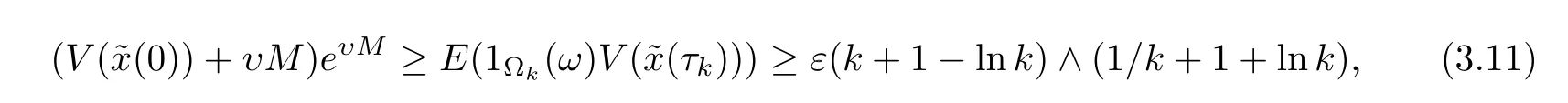
where 1Ωkis the indicator function ofk.Lettingk→∞，we get the contradiction∞＞(V((0))+υM)eυM=∞.

Thus，we must haveτ∞=∞.For system (3.2)，there is a unique global solution(t) ont≥0 with any given positive initial valueand the solution will remain inwith a probability of one.

Step 2Fort∈[0，τ]and for any initial conditionx(0)=(N(0)，T(0)，I(0)，u(0))∈，by Step 1，the system (3.2) has a unique global solution(t;0，x(0))∈that is defined and continuous on interval[0，τ]，hence system (2.2) also has a unique global solutionx(t;0，x(0))=on interval[0，τ].Att=τthere is an impulse which transfers solutionx(τ)=By similar arguments，we get that there is a unique global solutionx(t;τ，x(τ+))=～x(t;τ，x(τ+)) that is defined on[τ+，2τ]andIt is easy to see that the above deduction can repeated in finitely and the existence of solutions can be generalized tot→∞.This completes the proof. □

Proposition 3.4The solution (N(t)，T(t)，I(t)，u(t)) of system (2.2) with any given initial valueN(0)＞0，T(0)＞0，I(0)＞0，u(0)=0 has the properties that

Proof(i) From Lemma 3.2，there isandandt∈(nτ，(n+1)τ]，n∈Z+.Also，sinceu(0)＜¯u(0+)，we have

(ii) According to the first equation of (2.2) and It’s formula，we have that

Integrating this from 0 totand taking expectations of both sides，we obtain that

Then we get that

If 0＜p＜1，we obtain that

(iii) This is similar to the above discussion in (ii).

(iv) According to the third equation of (2.2)，we have that

so we have that

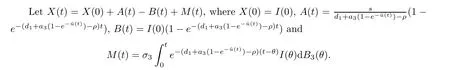
Applying the comparison theorem of the stochastic differential equation，we can easily getI(t)≤X(t) a.s.fort≥0.In addition，A(0)=0 andB(0)=0 imply thatSincewe obtain thata.s.ifd1+a3U＞ρ.

According to the strong law of large numbers for martingales，we therefore have that

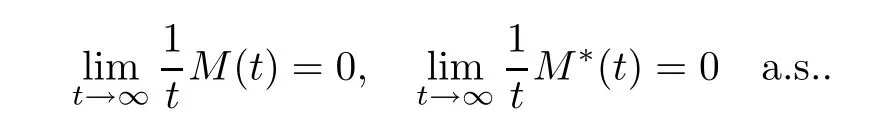
In addition，we have that

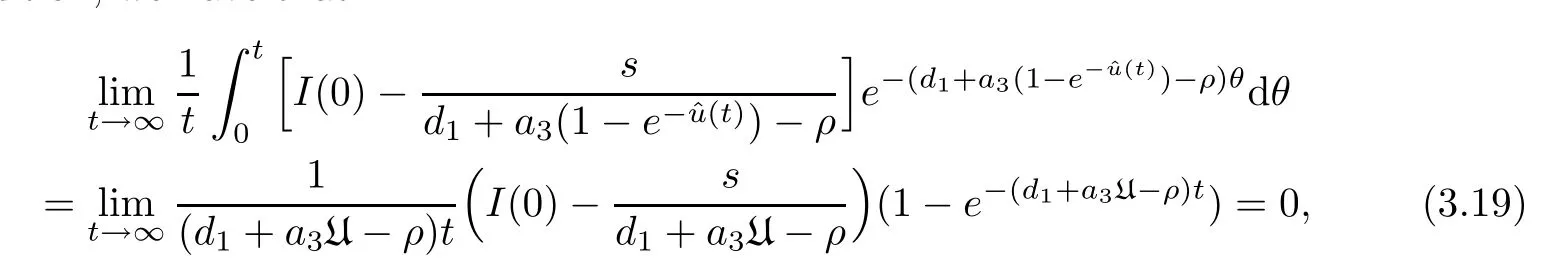
In what follows，we study the survival and extinction of tumor cells，and some of our analysis is motivated by the works of Liu[46]，Li[47]and Wei[48].

Theorem 3.5The cancer cellsT(t) modeled by system (2.2) satisfy that

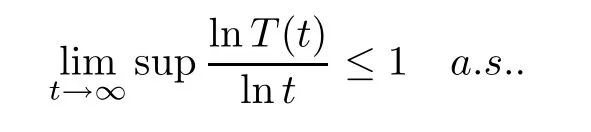
ProofAccording to the second equation of system (2.2)，it follows from the generalized It’s lemma that

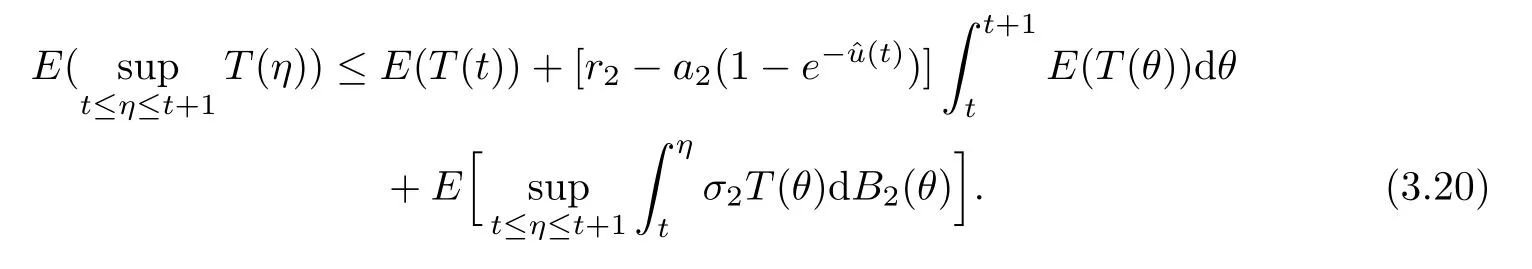
Furthermore，by the Burkholder-Davis-Gundy inequality and Hlder’s inequality，we can get that

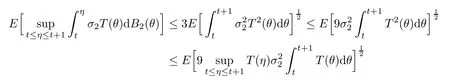
so we obtain that

By Proposition 3.4，we know that，so we have that

and there exists a positive constantM1such that

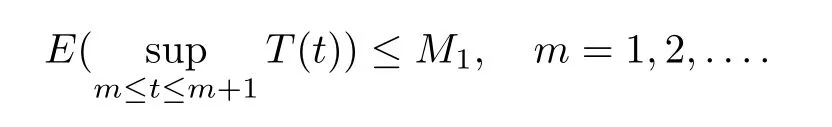
Let∈＞0 be an arbitrary constant.Then by Chebyshev inequality，we have that

and it follows from the Borel-Cantelli lemma that，for allω∈Ω，

holds for all but finitely manym.Hence，there must be am1(ω) which can guarantee that inequality (3.22) holds for almost allω∈Ω wheneverm≥m1.Thus we obtain that for almost allω∈Ω，

Remark 3.6In Theorem 3.5，we can further obtain that

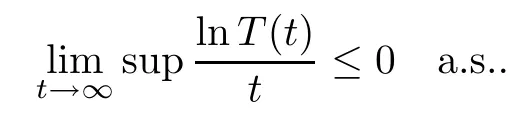
ProofNote that，according to Theorem 3.5，

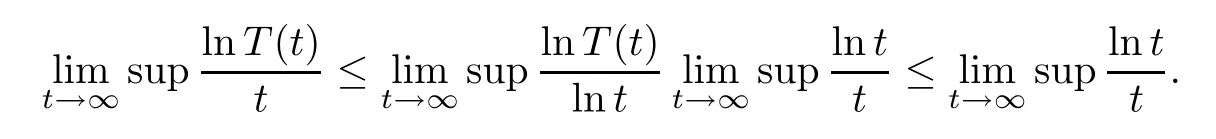
Theorem 3.7If，then the cancer cells modeled by system (2.2) will go to extinction almost surely，that is，a.s..

ProofApplying It’s formula to (2.2) gives that

Making use of the strong law of large numbers states yields thata.s..Furthermore，.Thus we obtain that

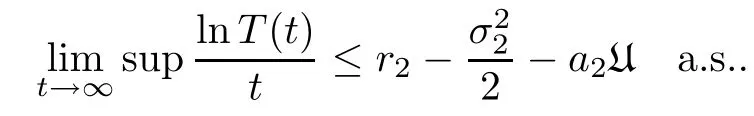
Theorem 3.8If，then the cancer cells modeled by system (2.2) will be non-persistent in the mean a.s.;that is，

ProofIt follows from (3.23) that

Integrating the above inequality fromt1tot，we get

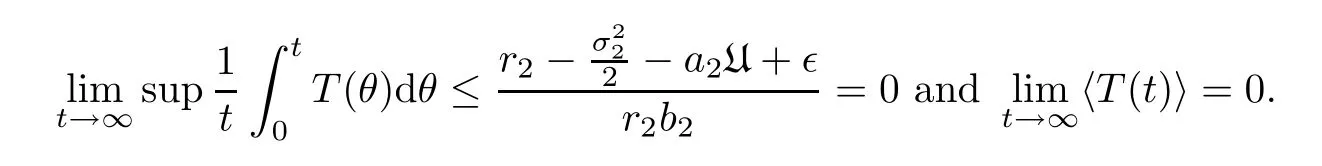
This completes the proof. □

Theorem 3.9Ifr1＞，then the cancer cells modeled by system (2.2) will be weakly persistent in the mean a.s.;that is，〈T〉*＞0.

ProofIn a fashion similar to the discussion of Theorem 3.8，we can obtain that ifr1＞then the inequality

It follows from Proposition 3.4 that ifd1+a3U＞ρ，then〈I(t)〉*=a.s..Also，in Remark 3.6，we have obtained thata.s..In what follows，we will prove thatP{〈T(t)〉*=0}=0.

Suppose thatP{〈T(t)〉*=0}＞0.It follows from (3.23) that

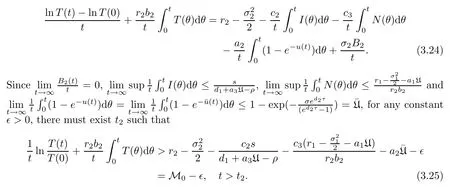
For anyω∈{〈T(t，ω)〉*=0}，we can easily get.Consequently，.Since∈＞0 is arbitrary，by letting∈→0，we obtain that，which is a contradiction witha.s..This completes the proof. □

Theorem 3.10Under the conditions of Theorem 3.9，we can further obtain that the cancer cells modeled by system (2.2) will be strongly persistent in the mean a.s..Moreover，

ProofIt follows from 3.25 that，whent＞t2，

In a manner similar to the discussion in Theorem 3.8，by lettingwe have that

Integrating the above inequality fromt2tot，we get that

Remark 3.11The conditions in Theorem 3.9 and Theorem 3.10 are the same，though we obtain the weak persistence and strong persistence of tumor cells in the mean by different methods.Obviously，if the strong persistence in the mean is established，then there must be weak persistence in the mean.

Remark 3.12From the perspective of cancer treatment，the conclusion of Theorem 3.7 is preferred.Compared with Theorems 3.9–3.10，Theorem 3.7 means that after a sufficiently long time，tumor cells will，with a large probability，be cleared.Both Theorem 3.9 and Theorem 3.10 show that the number of tumor cells can be very close to zero，but the survival ability of a tumor is better than that with Theorem 3.7.In practice，the growth of the tumor may be worse under this condition.

Remark 3.13It can be seen from the conditions listed in Theorems 3.7–3.9 that the key factors affecting the growth trend of tumor cells are the intensity of system stochasticity (σi) and the frequency (τ) and dose (σ) of drug delivery.Therefore，in the actual treatment，when the condition of Theorem 3.7 is not satisfied，the policy of drug input can be adjusted correspondingly in order to inhibit or eliminate tumor cells.

4 Numerical Simulations

In this section，by using the Euler Maruyama (EM) method[49]，we perform some numerical simulations to illustrate the main results in Section 3.We will also investigate the drug delivery tactics for chemotherapeutic treatment.Most model parameters are chosen from[8]and[20](refer to Table 1).

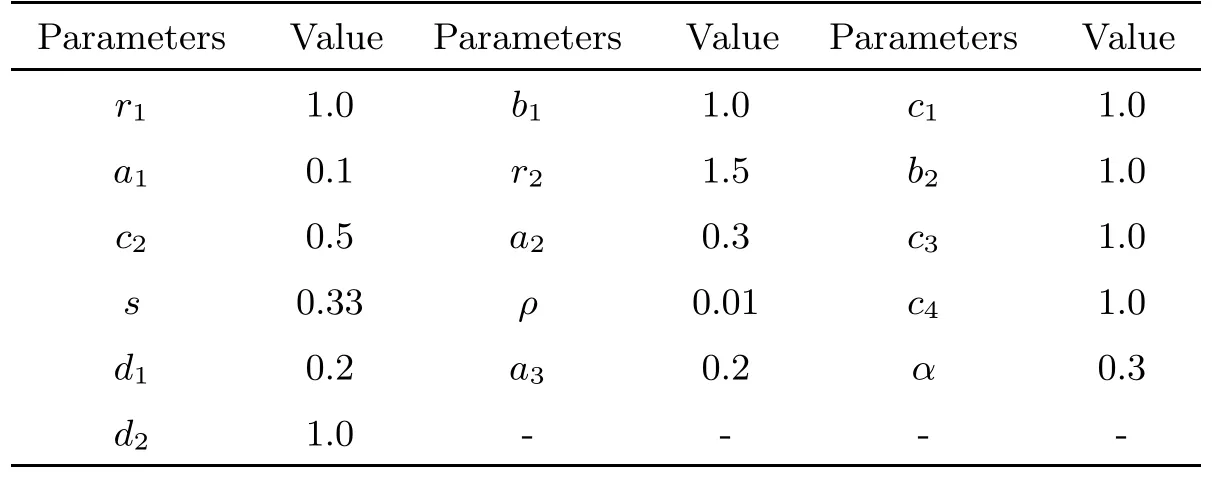
Table 1 Model parameter values from[8]and[20]

The initial cell levels are quite different.For the sake of comparison，in our simulation we choose a small initial immune levelI(0)=0.15，as was done in[8]，which describes a compromised immune system and is 10%below the healthy level.We also start with a relatively large tumor burden:T(0)=0.25.This is equivalent to a tumor with about 0.25×1011cells，or a sphere with a radius of between 1.8 and 3.9 cm.The clinical detection threshold of tumors is generally 107cells，so the initial tumor volume of 0.25 normalized units is above clinical detection levels ([8，50]).It needs to be mentioned that the presence of clinically detectable tumors before surgery does not necessarily mean that the tumor has been completely out of immune surveillance，and the therapy may only be falling into place because the immune system response is not enough to inhibit the rapid growth of a tumor cell population[8].

In Figure 1，we consider a strong stochasticity for the tumor cell number change and select noise powerσ1=0.05，σ2=1.6，σ3=0.05.For the chemotherapy，we choose the same drug dosage and delivery frequency as was done in[20];that is，σ=7 andτ=0.25.From this it can be deduced that，and according to Theorem 3.7，the cancer cells modeled by system (2.2) will go to extinction almost surely (see Figure 1).

Figure 1 The extinction of tumor cells of system (2.2)

Then we investigate the development of the tumor cell population with a relatively weak stochasticity for system (2.2) by setting the noise powerσ1=σ2=σ3=0.05.We first introduce a gentle chemotherapy regimen and deliver 4 units of drug every day;that is，σ=4 andτ=1.It is easy to verify that the condition list in Theorem 3.7 does not hold，and Figure 2 shows that the tumor cell population cannot be eliminated from the system.

Figure 2 Solutions of system (2.2) for σ1=σ2=σ3=0.05，σ=4 and τ=1

Keeping other parameters the same as in Figure 2，we enhance the intensity of chemotherapy to the level used in[20]，that is，σ=7 andτ=0.25，and we find that the tumor cells gradually disappear in the body (see Figure 3).From Figure 1，Figure 2 and Figure 3，we can observe that both strong noise powerand high intensity chemotherapy are important to inhibit the growth and survival of tumor cells.In addition，by comparing Figure 1 and Figure 3，we find that under the same chemotherapy mode，the tumor cells disappear in a much shorter time in Figure 1.This implies that the noise power plays the key role in determining the extinction of tumor cells.

Figure 3 Solutions of system (2.2) for σ1=σ2=σ3=0.05，σ=7 and τ=0.25

Furthermore，we also study the persistence of the tumor cell population.We keep the model parameters the same as in Table 1 and selectσ1=1，σ2=σ3=0.05 andσ=1，τ=2.Then by direct calculation，we getd1+a3U≈0.2290＞ρ=0.01 and.According to Theorem 3.9 and Theorem 3.10，the cancer cells modeled by system (2.2) will be strongly persistent in the mean a.s..However，from Figure 4 we can see that the growth of tumor cells is actually strongly persistent.On this basis，we try to adjust the intensity of stochasticity and the strategy of drug delivery to inhibit the growth of tumor cells.We take two different measures:one is to keep the same drug delivery but to reduce the stochasticity intensityσ1to 0.05;the other is to keep the same stochasticity intensity of the system but to change the drug input policy toσ=95 andτ=0.05.We find that tumor cells are cleared out after some time (see Figure 5).

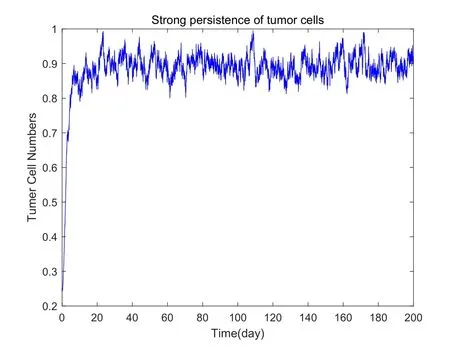
Figure 4 The strong persistence of tumor cells of system (2.2)

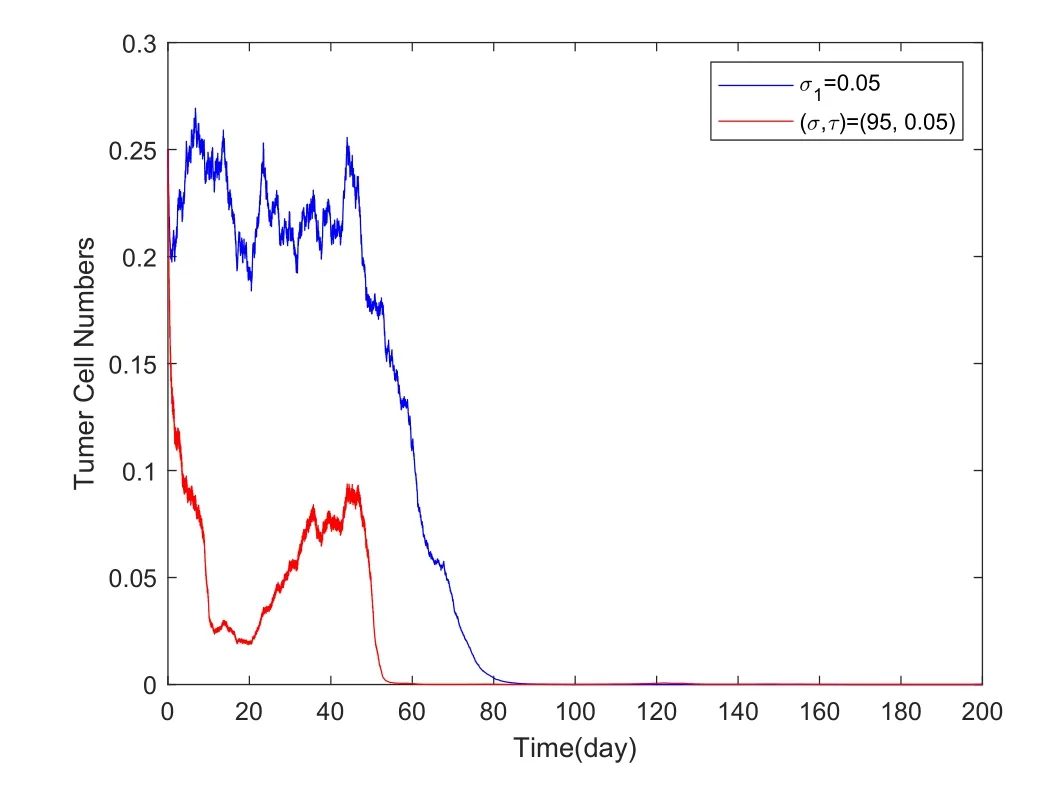
Figure 5 The impact of the stochasticity intensity and the drug input policy on the clearance of tumor cells

5 Conclusion

In recent years，many scholars have paid attention to the dynamics of tumor-immune systems with chemotherapy，and a large number of mathematical models have been constructed.However，most of the models are deterministic models，ignoring the random factors that can affect tumor growth and the regulation of an immune system.In addition，the existing stochastic models tend to be low dimensional ones，to reduce the difficulty of qualitative analysis，and some studies rely mainly on numerical analysis.Based on this situation，in this paper we have constructed a four-dimensional stochastic impulsive differential equation model to describe the interaction between cells and the immune system under the periodic impulsive input of chemical drugs，and studied the extinction and survival of the tumor cells.

First，a stochastic mathematical model describing the interaction and competition among normal cells，tumor cells and immune cells under periodically pulsed chemotherapy was established based on the deterministic model proposed by Pillis and Radunskaya in[8].Gaussian white noises were employed to mimic random fluctuation of the environment.Then，through qualitative analysis，conditions for the extinction，non-persistence in the mean，and weak and strong persistence in the mean of tumor cells were obtained.More precisely，it was found that

Combining our theoretical and numerical studies，we found that key factors affecting the growth trend of tumor cells are the intensity of the noise and the frequency and dose of drug delivery.We can adjust the intensity of stochasticity and the strategy of drug delivery to inhibit the growth of tumor cells.

For the persistence of tumor cells，we mainly focus on the persistence in the mean sense.For the stochastic persistence，we cannot give a good conclusion in theory，but in the numerical study，we can see that tumor cells can be stochastically persistent under the condition of strong persistence in the mean.In future research we will consider more methods and tools，and strive for a breakthrough in our understanding of stochastic persistence.Furthermore，new stochastic forms such as nonlinear perturbation and colored noise are also interesting in studying the growth trend of tumor cells for a tumor-immune system with chemotherapy.