THE EXISTENCE AND CONCENTRATION OF GROUND STATE SOLUTIONS FOR CHERN-SIMONS-SCHR ÖDINGER SYSTEMS WITH A STEEP WELL POTENTIAL*
2022-06-25JinlanTAN谭金岚YongyongLI李勇勇ChunleiTANG唐春雷
Jinlan TAN (谭金岚) Yongyong LI (李勇勇) Chunlei TANG (唐春雷)
School of Mathematics and Statistics,Southwest University,Chongqing 400715,China
E-mail:1695851214@qq.com;mathliyy518@163.com;tangcl@swu.edu.cn
Abstract In this paper,we investigate a class of nonlinear Chern-Simons-Schrdinger systems with a steep well potential.By using variational methods,the mountain pass theorem and Nehari manifold methods,we prove the existence of a ground state solution for λ>0 large enough.Furthermore,we verify the asymptotic behavior of ground state solutions as λ→+∞.
Key words Chern-Simons-Schrdinger system;steep well potential;ground state solution;concentration
1 Introduction and Main Results
In recent years,many authors have been interested in the nonlinear Schrdinger system
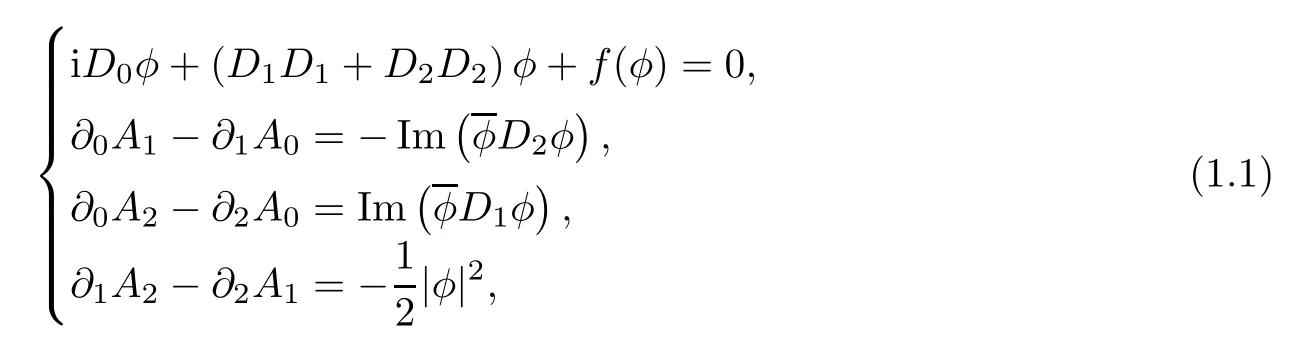
where i denotes the imaginary unit,for (t,x1,x2)∈R1+2,φ:R1+2→C is the complex scalar field,Aj:R1+2→R is the gauge field andDj=∂j+iAjis the covariant derivative for anyj∈{0,1,2}.The Chern-Simons-Schrdinger (CSS for short) system was proposed in[10–12]and consists of the Schrdinger equations augmented by the gauged fieldAj,which describes the nonrelativistic thermodynamic behavior of a large number of particles in an electromagnetic field.This feature of the model is important for the study of high-temperature superconductors,Aharovnov-Bohm scattering and the quantum Hall effect.Later,Bergé et al.[3]studied the blow up time-dependent solutions,and local well posedness was studied by Liu et al.in[20].
Inserting the standing wave ansatzφ=u(x)eiωt,u:R2→R,ω>0,andf(ueiωt)=f(u)eiωtinto system (1.1),if the gauge field satisfies the Coulomb gauge condition∂1A1+∂2A2=0,andAj(t,x)=Aj(x),j=0,1,2,then system (1.1) can be rewritten as
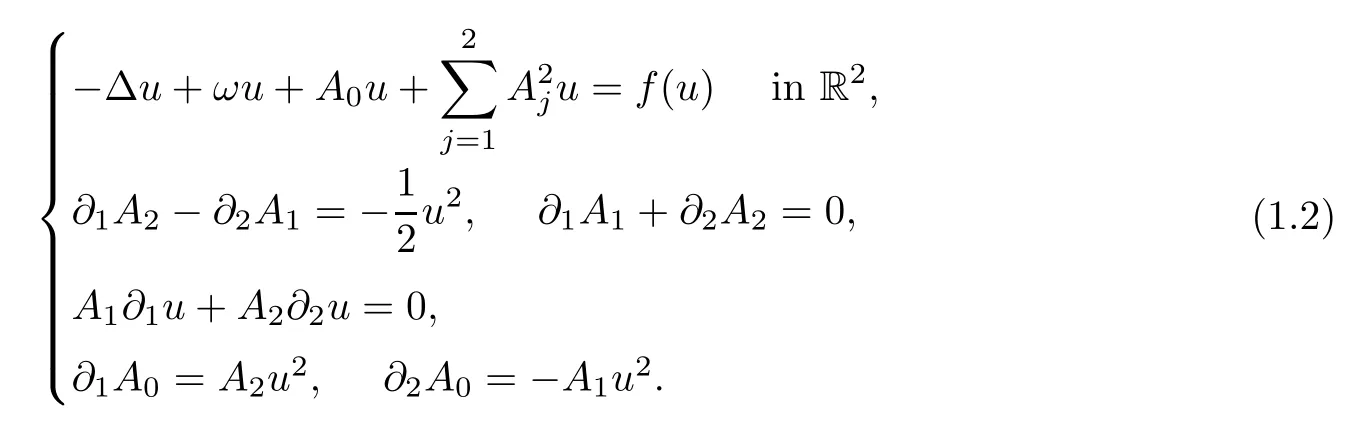
In[4],Byeon et al.first considered the standing wave solutions to system (1.2) of the form
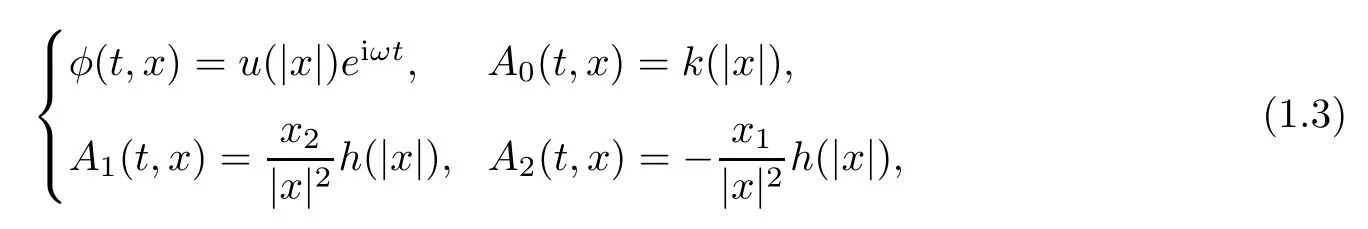
whereω>0 is a frequency andu,k,hare real valued functions depending only on|x|.Inserting the ansatz (1.3) into system (1.1),they got the nonlocal semilinear elliptic equation
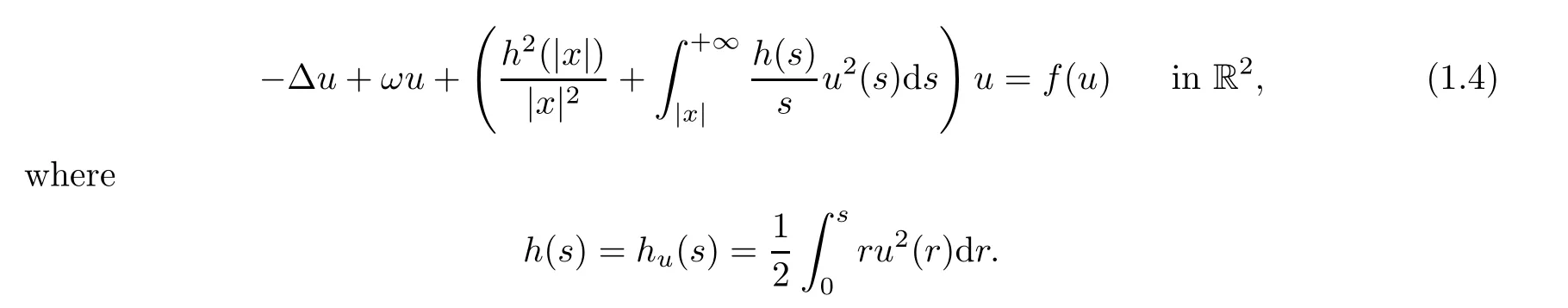
The existence and nonexistence results on nontrivial radial solutions of equation (1.4) have been shown forf(u)=μ|u|p-2u,p>2 andμ>0.After[4],many researchers studied the nontrivial solutions,sign-changing solutions,ground state solutions and semi-classical solutions of system (1.2);see e.g[5,9,16,18,22–24,26,31]and the references therein.More precisely,whenp>6,Huh[9]proved that equation (1.4) has in finitely many nontrivial solutions.For the case ofp≥4,Li and Luo[18]proved the existence,multiplicity and quantitative property of normalized solutions.Forp∈(2,4),Byeon et al.[4]first obtained the standing wave solutions to system (1.2) by using constrained minimization methods.Later,the above results have been extended in[22,23,31].In addition,many authors considered the more general cases of system (1.4);see,for example[7,8,25,32,34].In particular,normalized solutions and signchanging solutions of the CSS system were considered in[17,18,32,33].For whenfhas critical exponential growth,Li et al.[19]obtained the existence and concentrate behavior of positive solutions by using variational methods and the Trudinger-Moser inequality.In[15],Ji and Fang studied the existence and multiplicity of a positive solution for system (1.4) with critical exponential growth.Note that the above works relate to the autonomous cases of equation (1.4).For whenω>0 is replaced by a general potentialV∈C1(R2,R),which satisfies
(V)V(x) and∇V(x)·x≥0 a.e.in R2,by using the concentration compactness principle,Wan and Tang[28]studied the existence of nontrivial solutions for system (1.2) withf(u)=|u|p-2uandp>4.Moreover,forp>6,the authors in[6,27]proved the existence and concentration of semi-classical state solutions.
As for the CSS system with steep well potential,there have been few results presented so far.In[25],Tang et al.studied the existence and concentration for the solutions of equation (1.4) in(R2).After this work,Chen et al.[7]investigated the existence of sign-changing multi-bump solutions of equation (1.4).They considered equation (1.4) withωreplaced by the steep well potentialλV,whereV∈C(R2,R) is radial and satisfies the following conditions:
()V(x)∈C(R2),V(x)=V(|x|) andV(x)≥0 in R2;
() there exists some constantb>0 such thatVb:={x∈R2:V(|x|)<b}has a finite measure;
() there existsR>0 such that BR=intV-1(0) and,where BRdenotes the ball of radiusRcentered at 0.
Inspired by the above works,in the present paper,we intend to consider the existence and asymptotic behaviour of ground state solutions for the CSS system wherep∈(4,+∞),Vλ(x)=λV(x)+1 withλ>0,andVsatisfies the following assumptions:
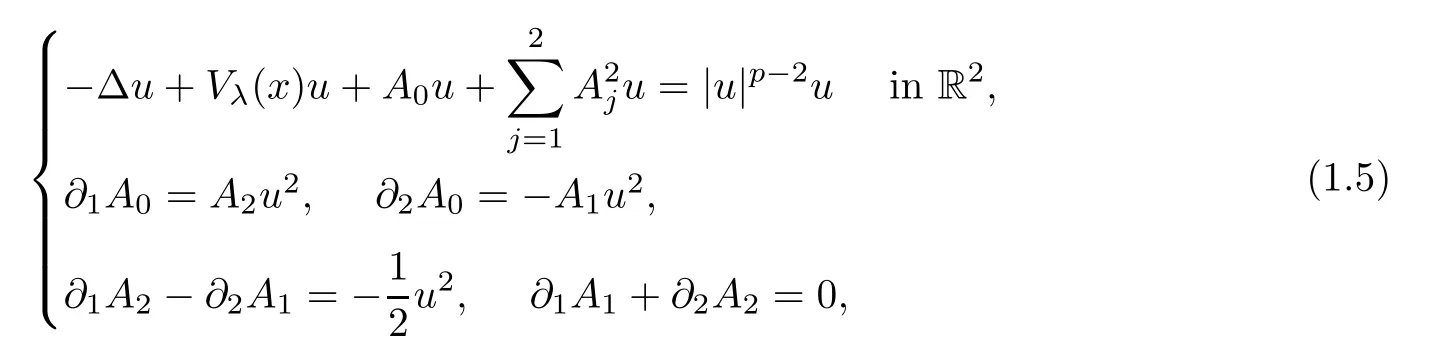
(V1)V∈C(R2,R) andV(x)≥0 in R2;
(V2) there exists someb>0 such that
(V3)Ω:=intV-1(0) is nonempty,has a smooth boundary,and=V-1(0);
(V4)V∈C1(R2,R),∇V(x)·x∈Lr1(R2) for somer1∈(1,+∞]and 2V(x)+∇V(x)·x≥0 a.e.in R2.
Our main results in this paper are stated as follows:
Theorem 1.1Assume that (V1)–(V3) are satisfied and thatp∈(6,+∞).Then there exists Λ>0 such that system (1.5) possesses a ground state solution for anyλ≥Λ.Moreover,for any sequence{λn}⊂[Λ,+∞) withλn→+∞,the sequence of solutions for system (1.5) converges tou0inH1(R2) up to a subsequence,whereu0∈(Ω) is a ground state solution of the system
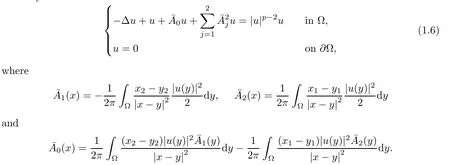
Theorem 1.2Assume that (V1)–(V4) are satisfied and thatp∈(4,6].Then there exists>0 such that system (1.5) admits a ground state solution for anyλ≥.Moreover,for any sequence{λn}⊂[,+∞) withλn→+∞,the solution sequence{uλn}of system (1.5) converges to a nontrivial solution of system (1.6) inH1(R2) up to a subsequence.
Remark 1.3This paper seems to be the first work on the CSS system with a steep well potential and subcritical nonlinearity inH1(R2).Our results extend the results of[25],which studied the CSS system with the general 6-superlinear nonlinearity and a steep well potential in(R2).As is known,we can easily deduce the boundedness of the (PS)csequence in the case ofp>6,while it is difficult to obtain the boundedness of the (PS)csequence in the case ofp∈(4,6].Many scholars applied the monotonicity trick developed by L.Jeanjean in[14]to overcome this difficulty.However,unfortunately,Jeanjean’s methods introduced in[14]seem to be invalid for our problem.In fact,if we use the monotonicity trick to demonstrate Theorem 1.2,we cannot deduce whether the (PS)csequence ofIλis uniformly bounded with respect toλ(even in the sense of upper limit),which is essential to proving the relative compactness of the (PS)csequence.Hence,in order to prove Theorem 1.2,we will use the methods in[13]to establish a (PS)csequence which asymptotically satisfies a Pohoˇzaev type identity.In addition,it is difficult to obtain the compactness of the (PS)csequence when we study the CSS system inH1(R2).We will use the methods of[2,21]to recover the lack of compactness by the appearance of a steep well potential.
We present the following notations,which will be applied throughout this paper:
·Lq(R2) is the Lebesgue space endowed with the norm

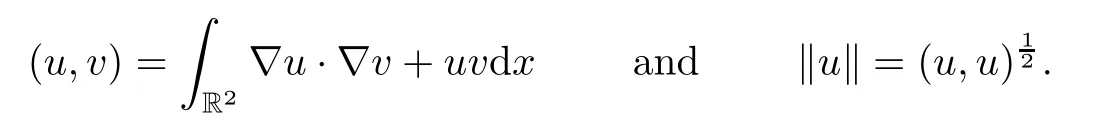
·(Ω) is a Hilbert space endowed with the scalar product
·E*,‖·‖E*denotes the dual space of the Banach spaceE,‖·‖E.
·R+:=(0,+∞),for anyr∈[0,+∞).
A few weeks later, my roommate Charlie and I were eating dinner at a Chinese restaurant. I shared this story about Ted s fortune cookie prediction, and his subsequent engagement. Just then, the waiter brought over our postmeal fortune cookies. Charlie laughed at the coincidence as we opened our cookies. Mine said, You have a magnetic personality. His said, You or a close friend will be married within a year. A chill ran up my spine9. This was really strange. Something told me to ask Charlie if I could keep his fortune, and he handed it to me with a smile.
·Cdenotes positive constant and is possibly various in different places.
2 Preliminaries
For anyλ>0,we define the following subset ofH1(R2):

Clearly,Eλis a Hilbert space when we equip it with the following inner product and the norm:
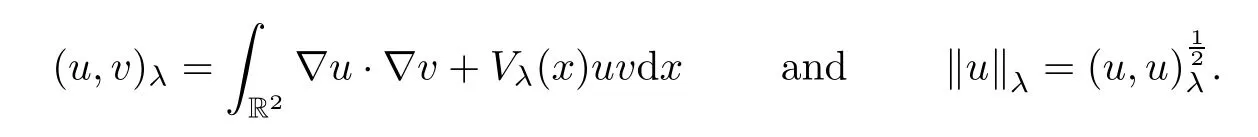
Due to (V1),we can deduce that ‖u‖≤‖u‖λfor allu∈Eλand anyλ>0.Then,for anyq∈[2,+∞),the embeddingis continuous and there exists somecq>0 such that

The componentsA1andA2in system (1.5) can be represented by solving the equations
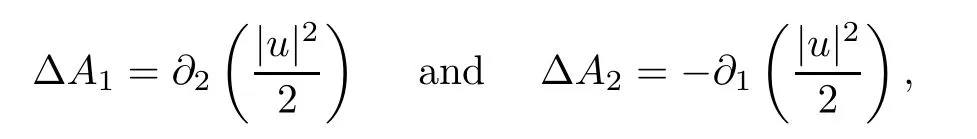
which provide the representation
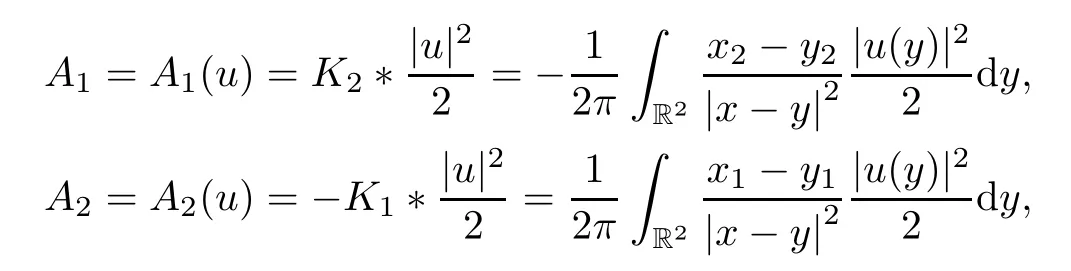
where*denotes the convolution,for anyx∈R2andj∈{1,2}.The identity ΔA0=∂1(A2|u|2)-∂2(A1|u|2) gives the following representation of the componentA0:
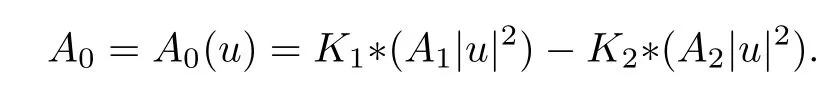
Thanks to[9],we known that the weak solutions of system (1.5) are precisely the critical points of the functionalIλ:Eλ→R defined by
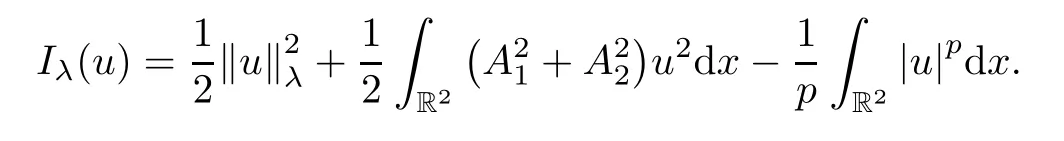
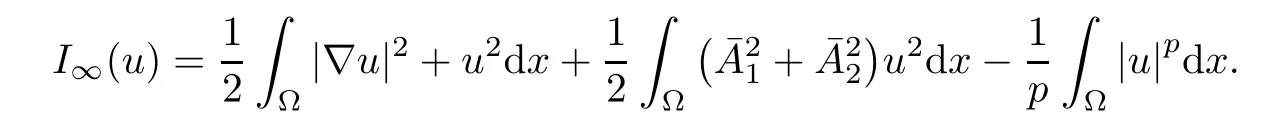
According to the Sobolev inequality (2.1),it is easy to see thatIλ∈C1(Eλ,R) and,for anyu,φ∈Eλ,

Through direct calculation,it holds that

Then,from (2.2) and (2.3),we obtain that,for anyu∈H1(R2),
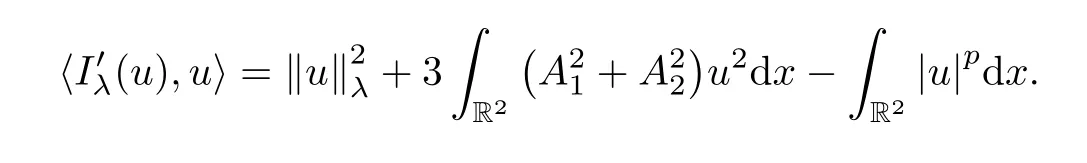
In view of[28,Proposition 2.7],any critical pointuofIλsatisfies the following Pohoˇzaev identity:
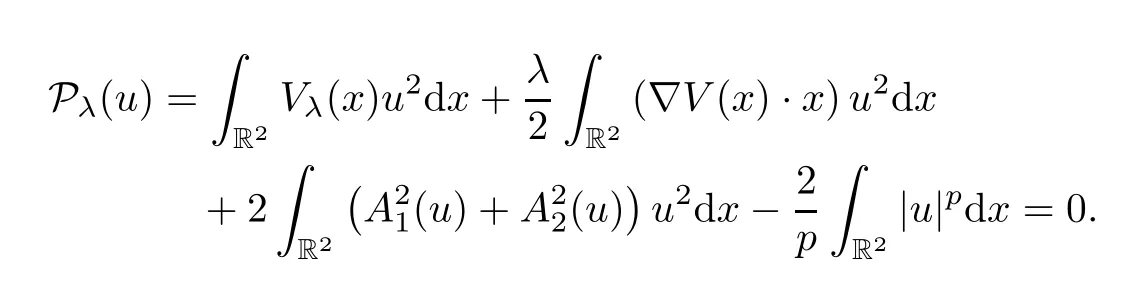
In order to prove our main results,we give the following propositions:
Proposition 2.1(Gagliardo-Nirenberg inequality,see[29]) For anyp∈[2,+∞),there exists some constantC(p)>0 such thatfor anyu∈H1(R2).
Proposition 2.2([28,Proposition 2.1]) Let 1<r<2 and.Then we have that

3 Proof of Theorem 1.1
First,we prove,by the mountain pass theorem,the existence of a ground state solution for system (1.5) whenp>6.Define the Nehari manifold and the least energy of system (1.5) as

Similarly,for the limit problem,system (1.6),we define its Nehari manifold and least energy as
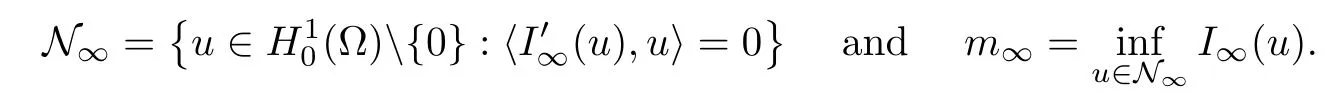
It is easy to see that N∞⊂NλandIλ(u)=I∞(u) for anyu∈(Ω).Then we getmλ≤m∞.
Lemma 3.1Suppose that (V1)–(V3) hold and thatp∈(4,+∞).Then,for anyλ>0,the functionalIλhas a mountain pass geometry;that is,
(1) there existρλ,αλ>0 such thatIλ(u)≥αλ>0 for all ‖u‖λ=ρλ;
(2) there existse∈Eλsuch that ‖e‖λ>ρλandIλ(e)<0.
Proof(1) Due to (2.1),we derive that,for anyu∈Eλ,
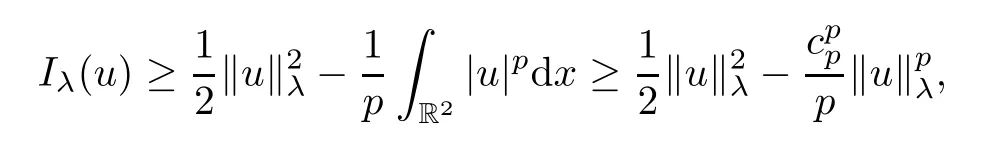
which shows that there exist some smallρλ,αλ>0 such thatIλ(u)≥αλfor any ‖u‖λ=ρλ.
(2) Takeu∈(Ω){0}and definewt(·)=tu(t·) for anyt>0.We easily obtain

Then it is easy to see thatsincep>4.Consequently,we can takee=wtwitht>0 large enough such that ‖e‖λ>ρλandIλ(e)<0.This lemma is proved. □
Recall that{un}⊂Eλis called a (PS)csequence ofIλifBy Lemma 3.1 and the mountain pass theorem[30,Theorem 1.15],Iλhas a (PS)cλsequence with
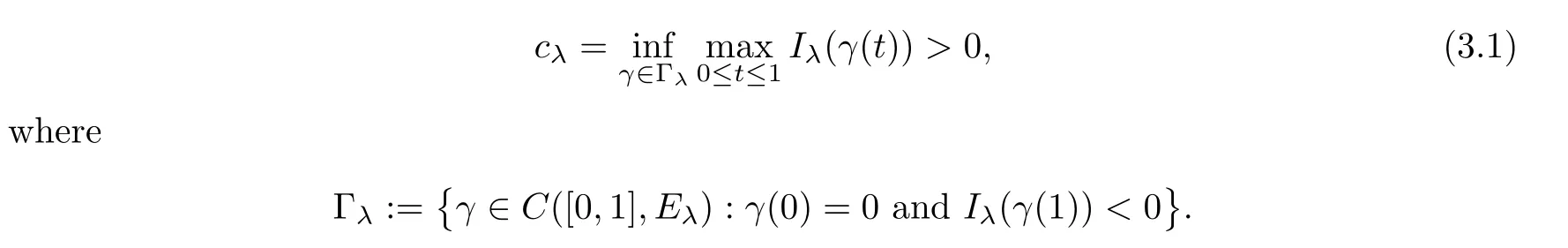
We claim thatcλ=mλ.Indeed,it is easy to show that,for anyu∈Eλ{0},there exists a uniquetu>0 such thattuu∈Nλ,and.Then we can prove as in[30,Theorem 4.2]thatcλ=mλfor anyλ>0.
Lemma 3.2Assume that (V1)–(V3) hold and thatp∈(6,+∞).Then there is some Λ>0 such that every (PS)csequence ofIλwithc∈(0,m∞]has a convergent subsequence for anyλ≥Λ.
ProofLetλ>0 and let{un}⊂EλsatisfyThen,for alln,

Consequently,there is some constant¯C>0 independent ofλsuch that
Clearly,{un}is bounded inEλ.Hence,up to a subsequence,there is au∈H1(R2) such that
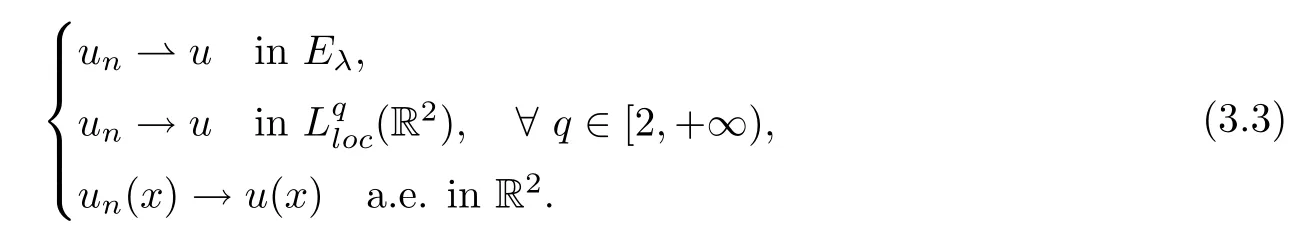
Due to the fact that{|un|p-2un}is bounded in,we obtain|un|p-2un⇀|u|p-2uinasn→∞.Then,for anyφ∈Lp(R2),it holds that,asn→∞,
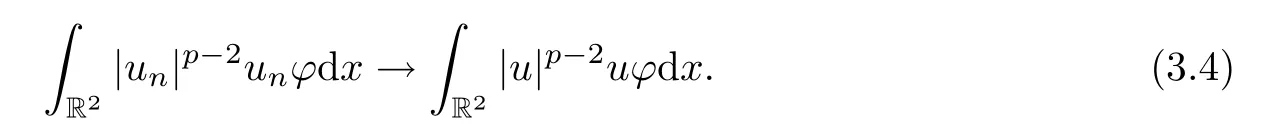
In fashion similar to the proof of Proposition 2.3-(2)(3),we have,for anyφ∈H1(R2) and asn→∞,that
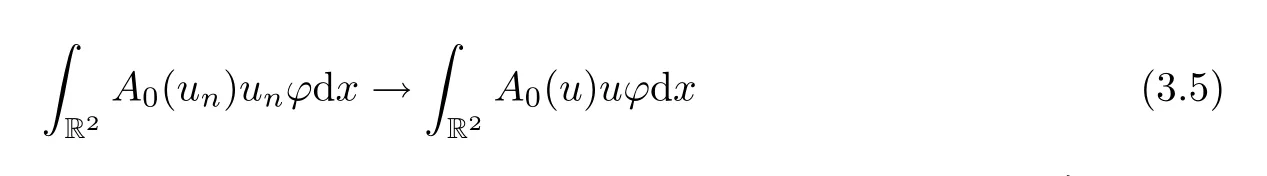
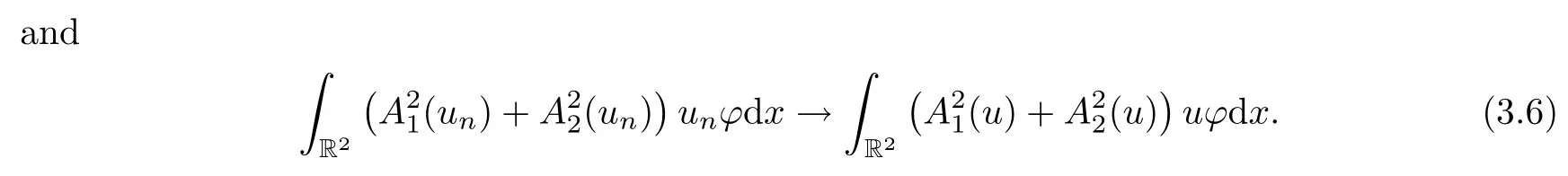
Thus,combining (3.4)–(3.6),we obtain thatLetvn=un-u.From Proposition 2.3-(4) and the Brézis-Lieb lemma (see[28,Lemma 1.32]),we get
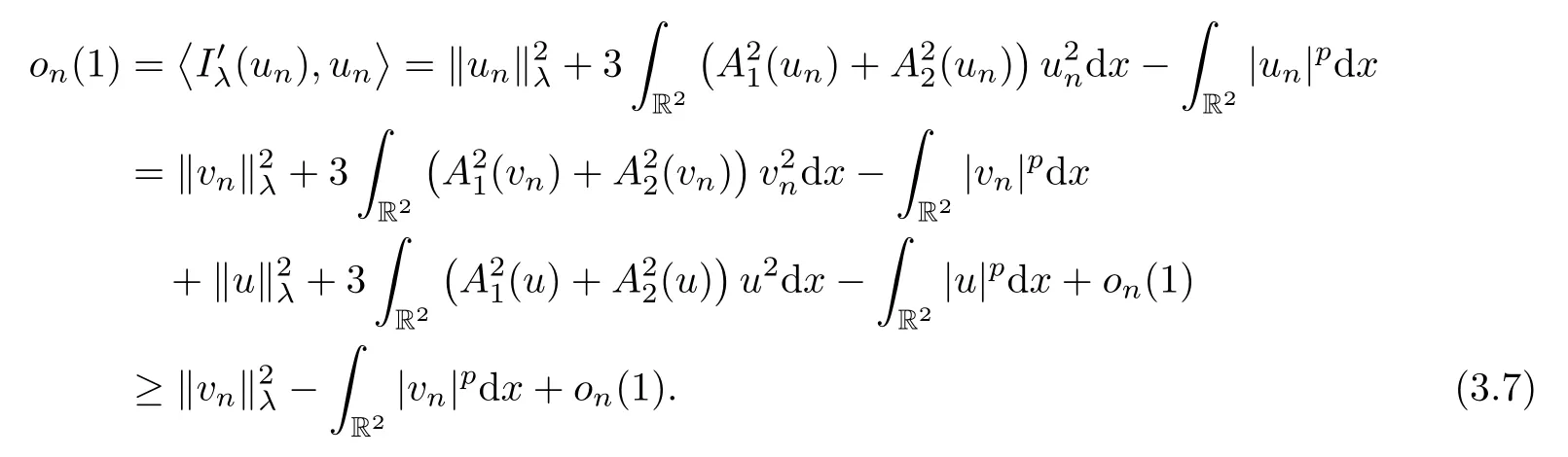
By (V1) and (V2),we get that
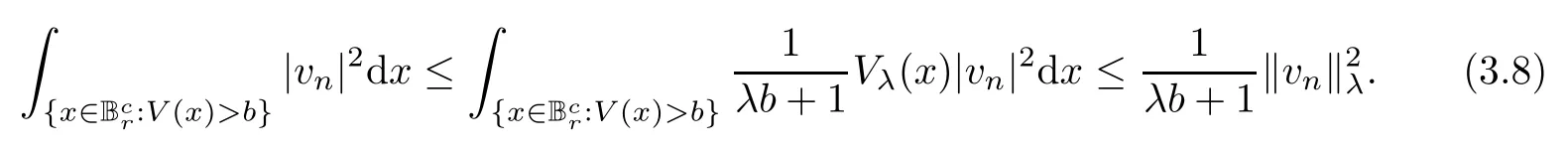
Moreover,it follows from (2.1),plus Hlder’s and Sobolev’s inequalities that,for someq∈[2,+∞),
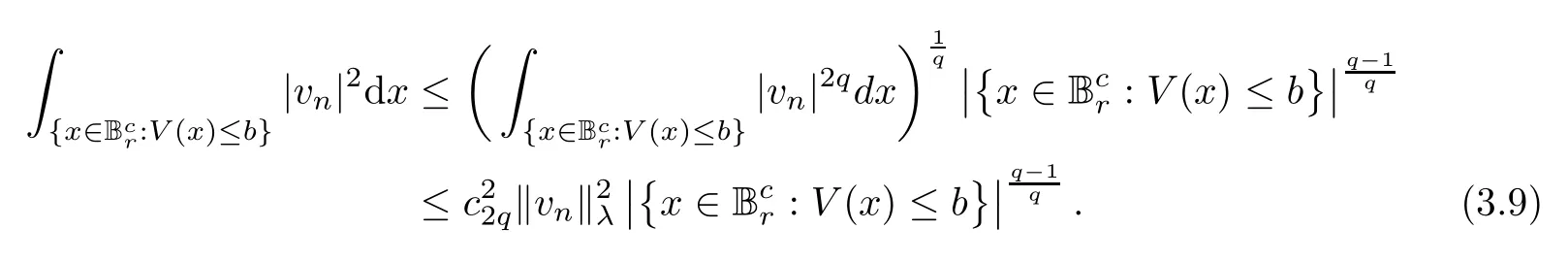
Then,by combining (3.3),(3.8) and (3.9),we obtain,asn→∞,
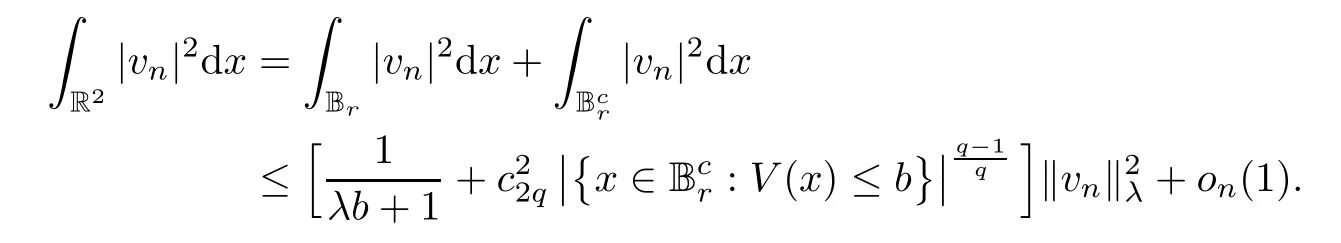
Furthermore,since (V2) implies,we derive from Proposition 2.1 and the Sobolev inequality that,forr>0 sufficiently large,
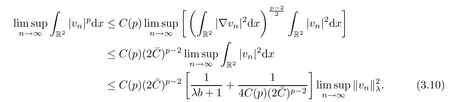
Now,combining (3.7) and (3.10),we have

Proof of Theorem 1.1First,we prove the existence of a ground state solution to system (1.5) for anyλ≥Λ.Sincecλ=mλ,by Lemma 3.1 and the mountain pass theorem,Iλhas a (PS)mλsequence{un}⊂Eλwithmλ∈(0,m∞].Then,according to Lemma 3.2,there exists someuλ∈Eλsuch thatun→uλinEλ.Naturally,we haveandNamely,uλis a ground state solution of system (1.5).
Second,we prove that the ground state solutions of system (1.5) converge to a ground state solution of system (1.6) asλ→+∞.For any sequence{λn}⊂[Λ,+∞) withλn→+∞,letuλn∈Eλnbe such thatfor eachn.Then,we have
Thus,{uλn}is bounded inH1(R2).Up to a subsequence,there exists au0∈H1(R2) such that
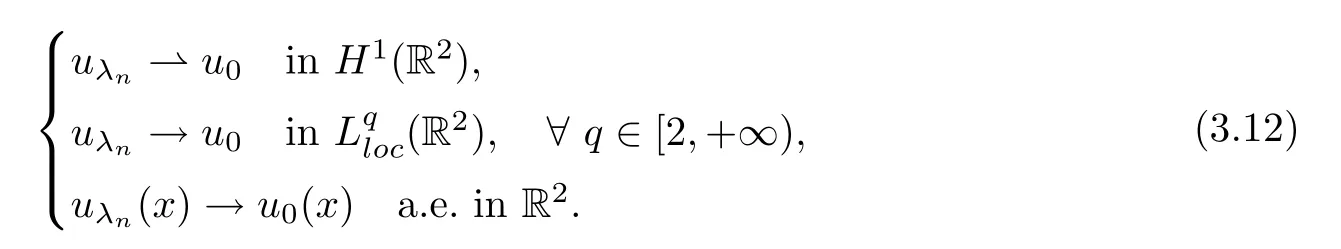
We claim thatu0∈(Ω).Indeed,combining (V1),(3.11),(3.12) and Fatou’s lemma,we have

Then,by (V3),it is easy to verify thatu0|Ωc=0.Furthermore,u0∈(Ω),since the boundary of Ω is smooth.Thereby,in a manner similar to the proof of (3.4),we deduce that,for anyφ∈Lp(R2),asn→∞,
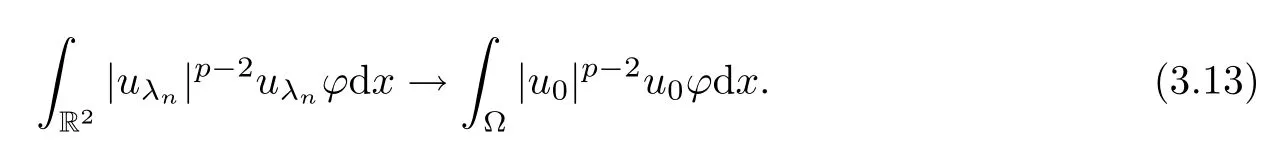
Moreover,in a manner similar to the proof of Proposition 2.3-(2)(3),fromu0|Ωc=0 we conclude that,for anyφ∈(Ω),asn→∞,

Thus,by (3.13)–(3.15),we obtain that.Lettingvλn=uλn-u0,sinceu0|Ωc=0,it is easy to see that{‖vλn‖λn}is bounded.Then,asn→∞,
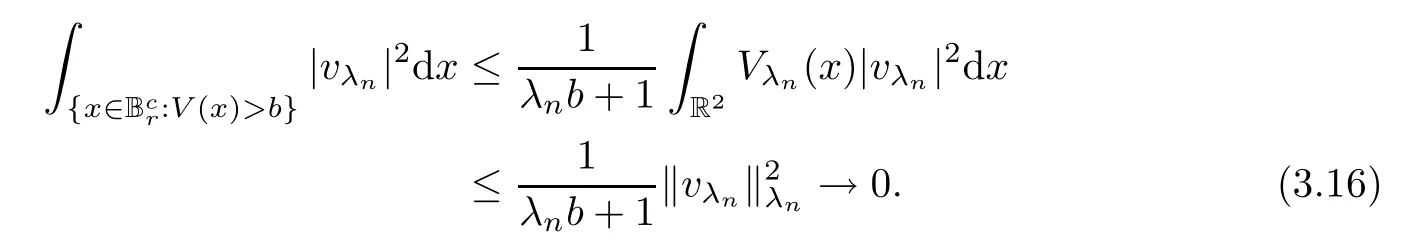
Since (V2) implies that,by using (2.1),plus Hlder’s and Sobolev’s inequalities,we obtain that,forq∈[2,+∞),
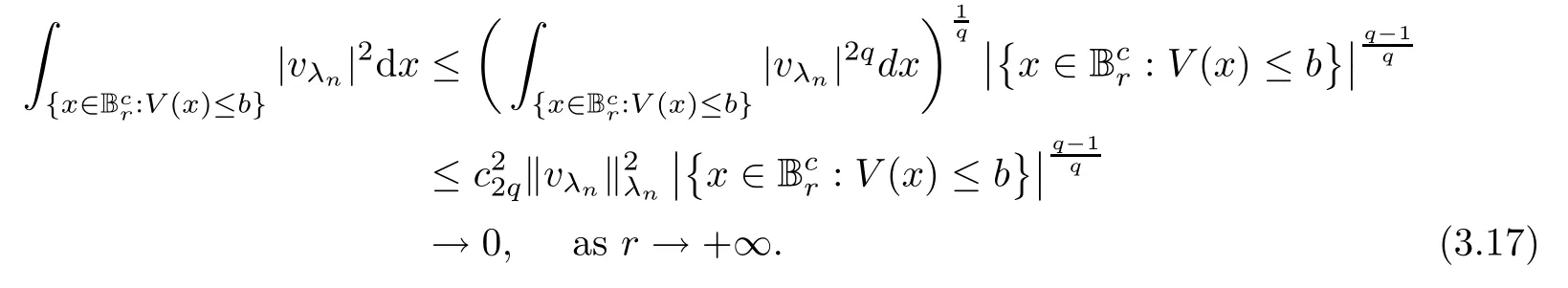
Then,by (3.12),(3.16) and (3.17),we getvλn→0 inL2(R2).In a manner similar to (3.10),we obtain that

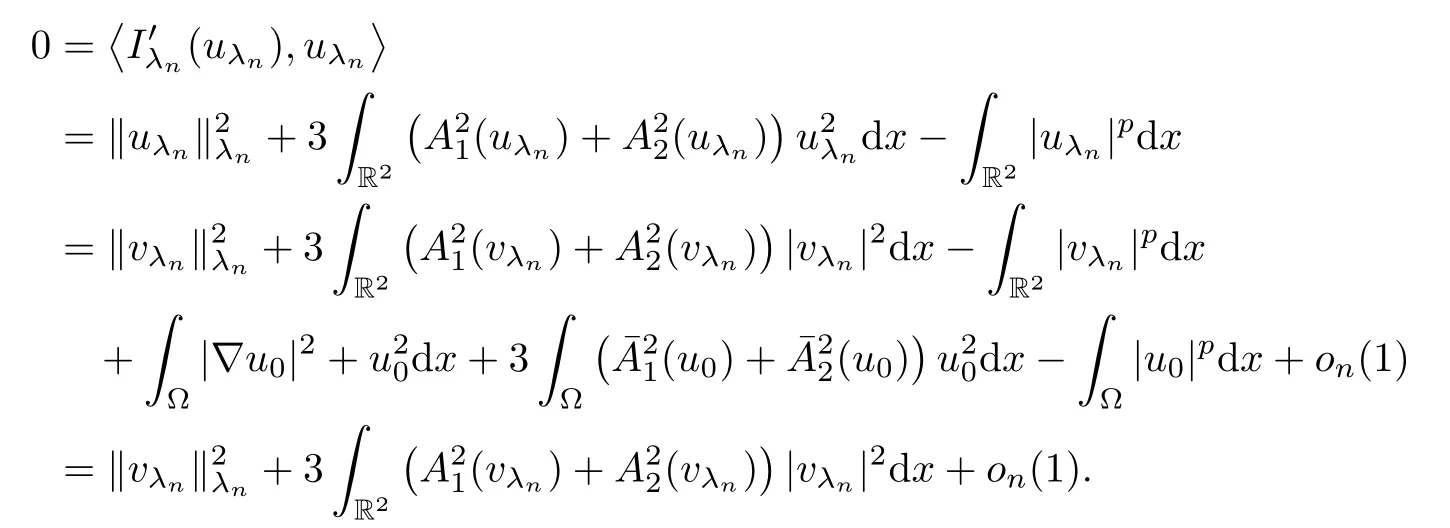
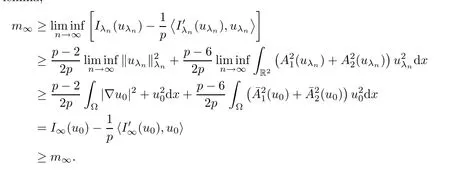
That is to say,I∞(u0)=m∞.Thus,u0is a ground state solution of system (1.6).Due to the above discussion,we have completed the proof of Theorem 1.1. □
4 Proof of Theorem 1.2
As is well known,it is difficult to prove the boundedness of (PS)csequence for system (1.5) withp∈(4,6].To conquer this difficulty,motivated by[4,28],we introduce the auxiliary functional
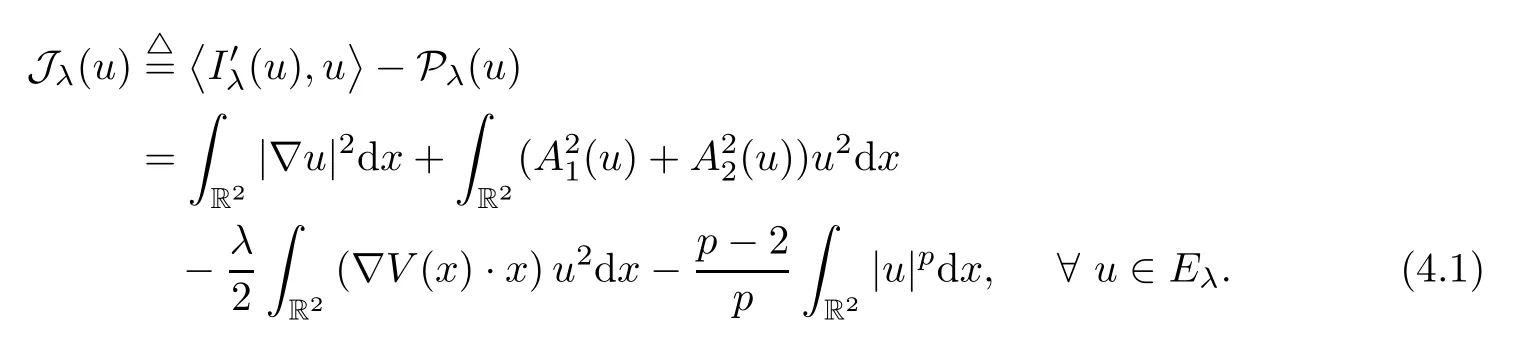
In the following lemma,in a fashion similar to[13],we establish a (PS)csequence{un}with
Lemma 4.1Assume that (V1)–(V4) hold and thatp∈(4,6].Then,for anyλ>0,there exists a sequence{un}⊂Eλsuch that,asn→∞,
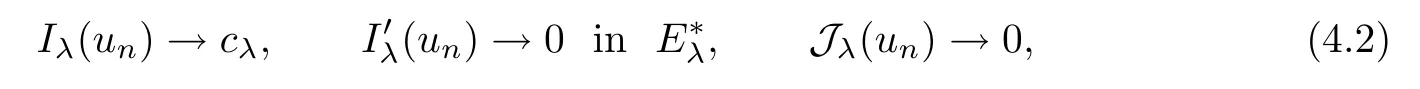
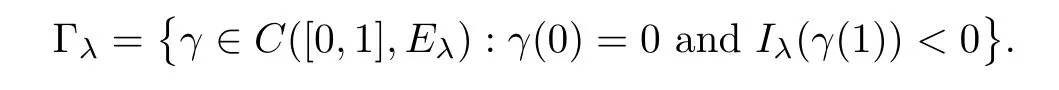
ProofFirst,we derive from Lemma 3.1 thatIλhas a mountain pass geometry and that the mountain pass value is characterized by (3.1).Next,following the idea of L.Jeanjean in[13],we set the mapQ:R×Eλ→EλbyQ(θ,v)(·)=eθv(eθ·) for any (θ,v)∈R×Eλ.Then the functionalIλ°Qis composed of

It is easy to show that the functionalIλ°Qis continuously Fréchet-differentiable in R×Eλand that

for any (θ,v),(h,w)∈R×Eλ.Set the family
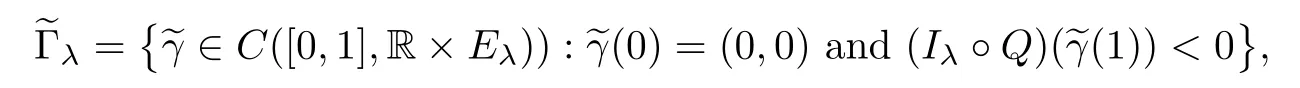
which defines a minimax level
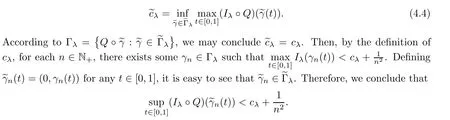
Furthermore,as a result of the general minimax principle (see[30,Theorem 2.8]),there exists a sequence{(θn,vn)}⊂R×Eλsuch that,asn→∞,

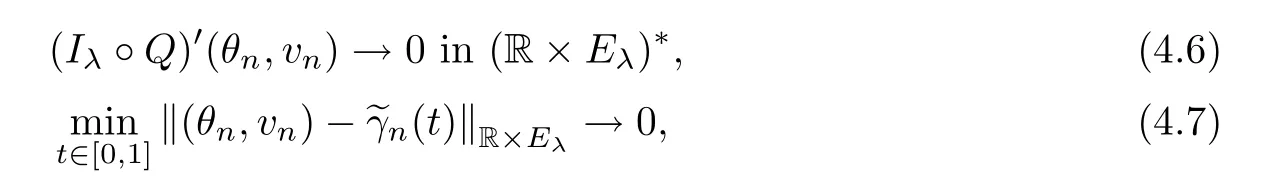
where ‖·‖R×Eλis the norm of the product space R×Eλ.Now,takeun=Q(θn,vn).It easily follows from (4.5) thatTesting (Iλ°Q)′(θn,vn) with (1,0),we can conclude that

which leads to Jλ(un)→0 asn→∞.Moreover,noting that (4.7) impliesθn→0,we consider the functionQ(-θn,φ) for anyφ∈Eλ.By the mean value theorem,we deduce that,for alln,
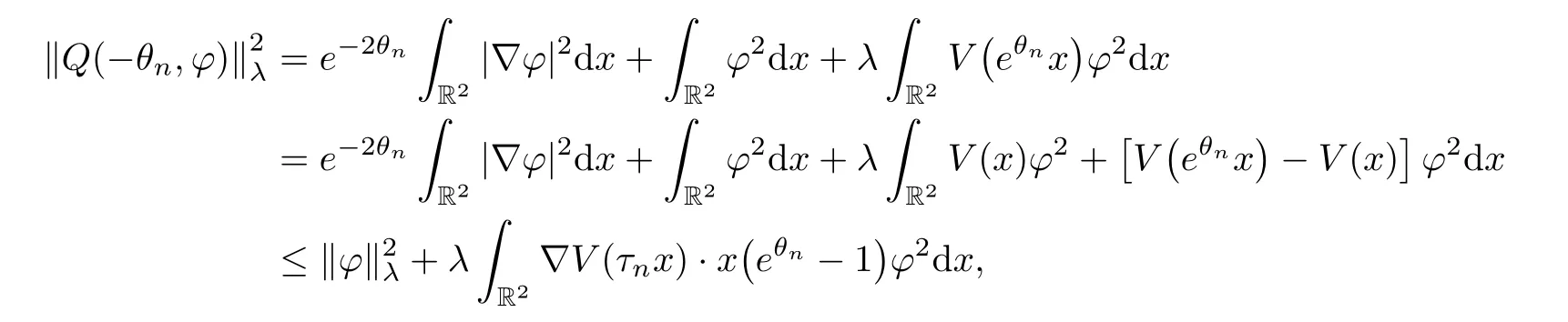
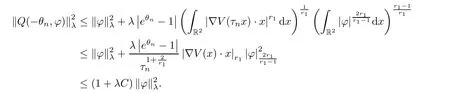
Similarly,ifr1=+∞,it follows from (V4) and the Sobolev inequality again that,for alln,

Therefore,letting (0,Q(-θn,φ)) be a testing function in (Iλ°Q)′(θn,vn),we may derive from (4.6) that

As in the proof of Lemma 3.1,we may conclude thatI∞has a mountain pass geometry forq∈(4,6]and the corresponding mountain pass value is described as the minimax level
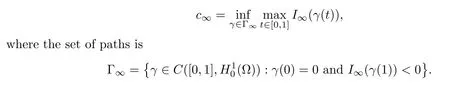
Therefore,in a fashion similar to Lemma 3.2,we will verify the local (PS)ccondition ofIλforλlarge enough.
Lemma 4.2Assume that (V1)–(V4) hold and thatp∈(4,6].Then there exists some>0 such that,for anyλ≥,every (PS)csequence{un}⊂EλofIλwithandc∈(0,c∞]admits a convergent subsequence.
ProofFrom the definition of{un}and (V4),it easily follows that

Consequently,there exists some constantindependent ofλsuch thatFurthermore,repeating the relevant arguments from the proof of Lemma 3.2,we conclude that there exists a constantsuch that each sequence{un}⊂Eλsatisfying (4.2) is relatively compact onceThus we have completed the proof of this lemma. □
Proof of Theorem 1.2First,we prove the existence of a ground state solution to system (1.5) for anyλ≥~Λ.To this and,we introduce the following set of weak solutions:
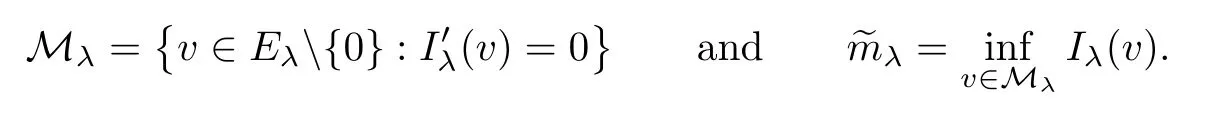
By the definitions ofcλandc∞,we easily derive fromthatcλ≤c∞for allλ>0.Then,due to Lemmas 4.1 and 4.2,there existswλ∈Eλsuch that(wλ)=0 andIλ(wλ)=cλ.Naturally,it results that MλØ andλ≤cλ.Take{vn}⊂Mλas a minimizing sequence forλ.According to〈(vn),vn〉=0 and (2.1),we have that
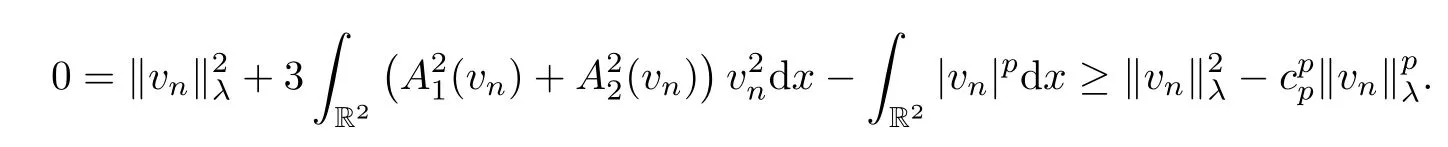
Then there exists someδλ>0 such that ‖vn‖λ≥δλfor alln,which,together with (V4),implies that
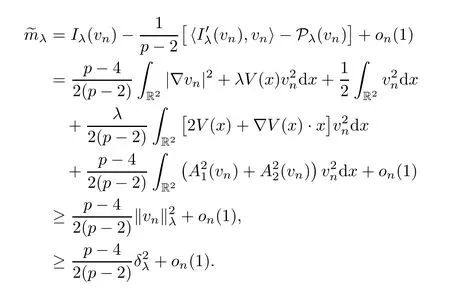
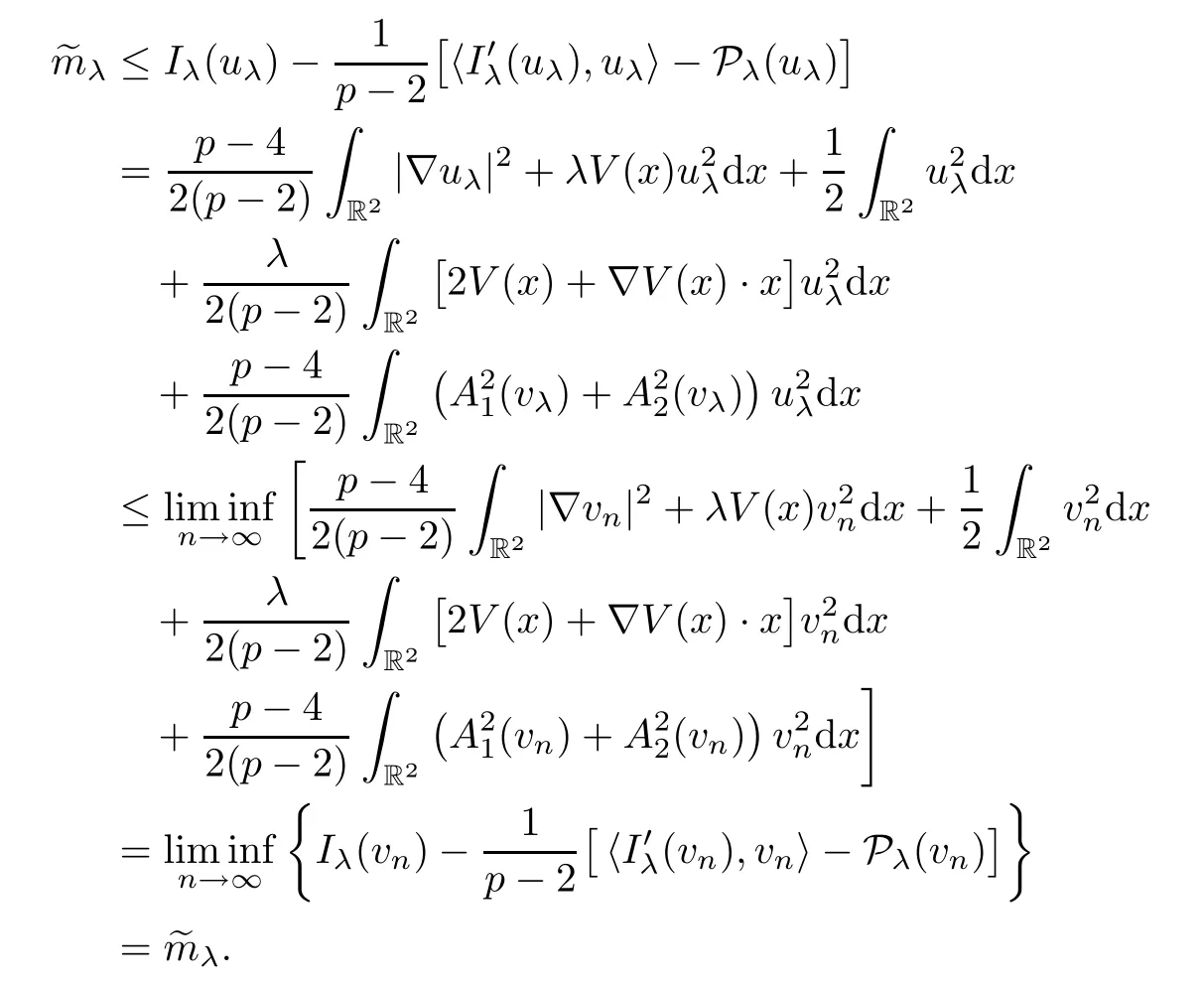
Second,we prove the concentration of ground state solutions to system (1.5) asλ→+∞.For any sequencesuch thatλn→+∞,letuλn∈Eλnbe such that0 andIλn(uλn)=~mλnfor eachn.Observing Pλn(uλn)=0,we deduce from (V4) that
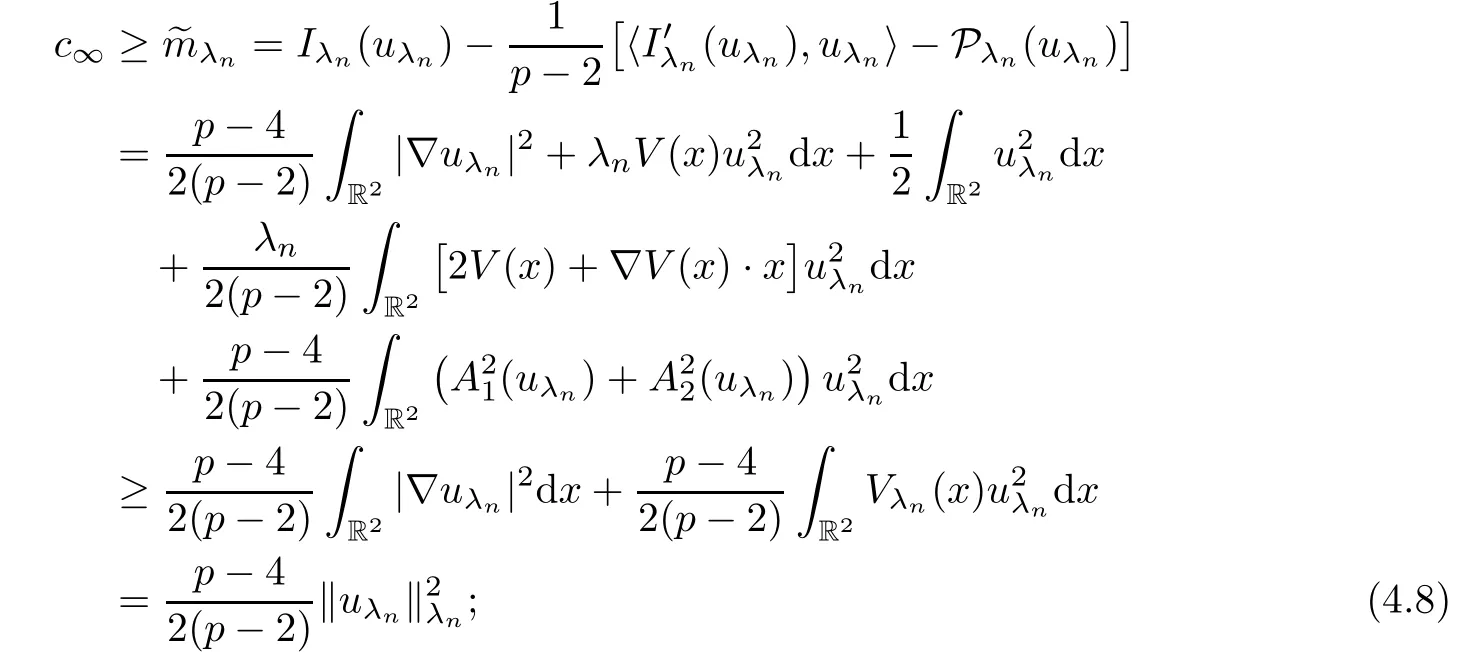
that is,{‖uλn‖λn}is bounded.Then,repeating the relevant arguments from the proof of Theorem 1.1,we deduce,up to a subsequence,that there exists somesuch that ‖uλn-u0‖λn→0.Obviously,uλn→u0inH1(R2).Moreover,byand the Sobolev inequality,
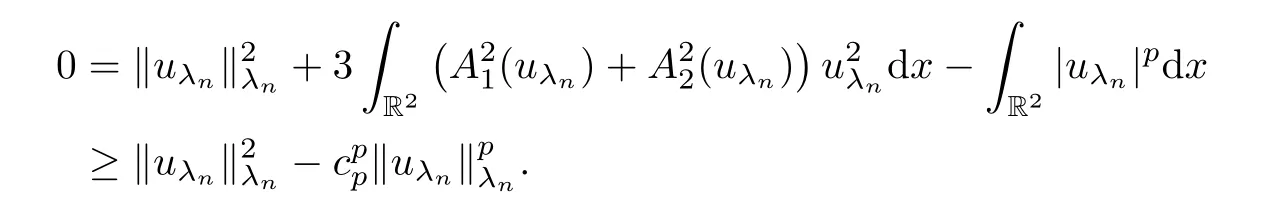
猜你喜欢
杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- A ROBUST COLOR EDGE DETECTION ALGORITHM BASED ON THE QUATERNION HARDY FILTER*
- CONTINUOUS SELECTIONS OF THE SET-VALUED METRIC GENERALIZED INVERSE IN 2-STRICTLY CONVEX BANACH SPACES*
- EXISTENCE RESULTS FOR SINGULAR FRACTIONAL p-KIRCHHOFF PROBLEMS*
- BOUNDS FOR MULTILINEAR OPERATORS UNDER AN INTEGRAL TYPE CONDITION ON MORREY SPACES*
- LEARNING RATES OF KERNEL-BASED ROBUST CLASSIFICATION*
- A COMPACTNESS THEOREM FOR STABLE FLAT SL (2,C) CONNECTIONS ON 3-FOLDS*
