基于特征加权模糊聚类的电力负荷分类

2022-06-24马宗彪许素安朱少斌王晶

中国电力 2022年6期

马宗彪，许素安，朱少斌，王晶

(中国计量大学机电工程学院，浙江杭州 310018)

0 引言

近年电力市场广泛发展，供电侧及电力需求侧管理技术的普遍应用，电力系统的负荷分类已成为电力规划、定制电价、负荷预测、负荷建模等工作的基础性研究内容[1]。因此，深入研究电力系统的负荷分类方法，有利于研究掌握客户负荷的变化趋势，对供电侧的科学管理用电工作具有重要意义。

电力负荷曲线是描述电力负荷需求随时间变化的特性曲线[2]。在实际应用中，通常采用具有代表性的典型季节的日负荷曲线，将典型的日负荷曲线进行归一化处理，可得到典型日最大(小)负荷、平均负荷率等信息。针对电力负荷的特征提取及聚类算法，国内外学者进行了相当深入的研究工作。目前较为流行的聚类方法有K-means[3]、支持向量机[4]、模糊C均值[5]、自组织特征映射神经网络（SOM）[6]等，其中聚类算法能够深入挖掘数据的隐性规律，具备无监督学习能力。在文献[7]提出的模糊集理论基础上，模糊C均值聚类在样本模糊隶属度上，增强了样本的类属程度和分类准确性，因此得到广泛关注。

欧式距离不仅是聚类分析，更是模糊C均值聚类分析中最常用的距离度量方法[8]。在欧式距离与FCM聚类分析相结合的研究之中，包含加权欧氏距离和非加权欧氏距离[9]，根据加权欧式距离的性质，权值系数变化能够明显改变欧式距离的大小，因此根据实际应用，确定权重系数，并利用加权欧式距离进行聚类分析具有科学依据[10]。

本文考虑直接从供电侧记录的用户负荷数据入手，对原始数据进行除坏点、归一化等预处理操作后，求取每个用户的典型日负荷曲线。其次，将变分模态分解中模态带宽问题转化为约束优化求解，并对每阶模态进行Hilbert变换，不断更新模态（IMF）分量中心频率和频带宽，从而避免信号模态混叠。利用变分模态分解对负荷曲线分别进行3、4、5阶模态分解和构造优化，得到重构的负荷曲线数据。最后，在欧式距离d上引入权重系数w，将负荷曲线进行特征加权，利用模糊C均值聚类算法（fuzzy C-means，FCM）对分解后重构的负荷曲线进行聚类分析，使得各时段具有不同的权重。引入典型的聚类有效性函数P'(U,c)作为判断最佳聚类数目c的依据，进而挖掘客户间不同个体的用电负荷特性规律，将负荷曲线形态相似的归为一类，从而将对应的企业归为同类负荷群体。

1 模态分解及聚类算法描述

1.1 特征加权FCM算法

FCM算法是一种基于目标函数的模糊聚类算法，主要用于数据的聚类分析，是一种柔性的模糊划分方法[11]。其核心思想是使被划分到同一类的对象之间相似性最大，不同类之间相似性最小。为了借助目标函数达到求解最优聚类的问题，研究者利用均方逼近法构造了带约束的非线性规划模型，从而来求解最优聚类。

定义数据集合X={x1,x2,…,xn}为样本数据集，n为样本总数，则FCM算法目标函数Jm定义为

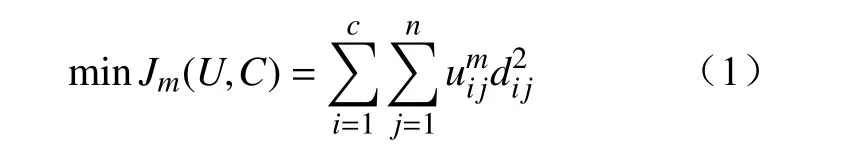
式中：C为聚类中心矩阵；c为聚类数目；m为隶属度矩阵U的加权指数(m>1)；n为样本总数；dij=||xi-ci||为传统的欧几里得距离，表示第i个样本xi到第i个聚类中心ci的距离；uij为隶属度矩阵U的元素，表示第i个样本到第j个聚类中心的隶属度，且满足

应用拉格朗日乘数求解目标函数Jm的条件极值，通过求取偏导得到隶属度函数uij以及第i类的聚类中心ci分别为

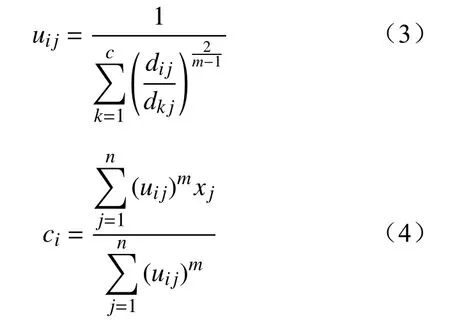
特征加权FCM算法为在传统欧氏距离dij的基础上[12]，引入各维度的特征权重系数w={w1,w2,…,wn}，以此来考虑各个特征对分类结果的不同影响，即假定待分析的样本各维特征对分类结果的影响程度为w。传统欧氏距离dij及加入权重w的欧几里得距离dij*表示为

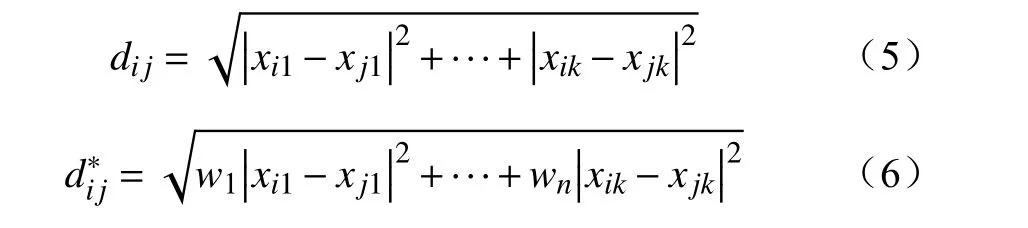
基于特征加权的欧氏距离dij*，目标函数Jm、隶属度函数uij及聚类中心函数ci中的欧氏距离dij相对应变为加权欧氏距离dij*。

1.2 VMD算法

VMD算法是一种非递归性的变分模态分解方法，通过迭代来求解变分函数最优解，适用于对非线性信号进行分解和重构[13]。针对EMD算法对信号及采样点敏感的问题，文献[14]于2013年将经典维纳滤波器推广到多个自适应频带，利用乘法算子交替方向法（alternate direction method of multipliers，ADMM）对变分模型进行合理优化，提出完全非递归的变分模式分解模型。VMD算法在电力负荷的特征提取方面鲜有研究，其中的维纳滤波器可有效抑制负荷的噪声和干扰[15−16]，对相近负荷的特征频率进行有效分离，具有良好的鲁棒性。

VMD算法可通过构造求解约束变分使原始信号分解为数个IMF分量[17]。可假定将信号f分解为K阶模态，相应变分构造问题概述如下。

（3）利用高斯平滑指标估计出各阶模态IMF分量信号带宽，可得约束变分问题为

式中：f为待解析信号，k为待解析模态数量，{uk}={u1,u2, …,uk}表示解析所得K阶模态IMF分量，{ωk}={ω1,ω2, …,ωk}表示各 IMF 分量中心频率。

通过引入Lagrange函数可将上述约束性变分问题转换为非约束性变分问题，从而求取其最优解，即

2 基于加权VMD-FCM算法的负荷分类

在电力系统中，用户原始数据直接来源于电力采集系统，然而由于动态的数据在采集过程中偶有通道拥堵、中断等不良故障，严重影响负荷研究工作的准确性[19]。同时，在负荷特性提取方面，单一权重的负荷特征不能准确地表示实际负荷特性，在实际应用中存在一定的局限性。本文提出基于特征加权的VMD-FCM算法，利用VMD算法在数据处理方面的良好的鲁棒性，能有效解决模态混叠等问题。并且引入特征加权系数，使FCM聚类分析算法在聚类时更好地与实际情况相结合。图1为特征加权VMD-FCM算法应用于负荷分类的流程。

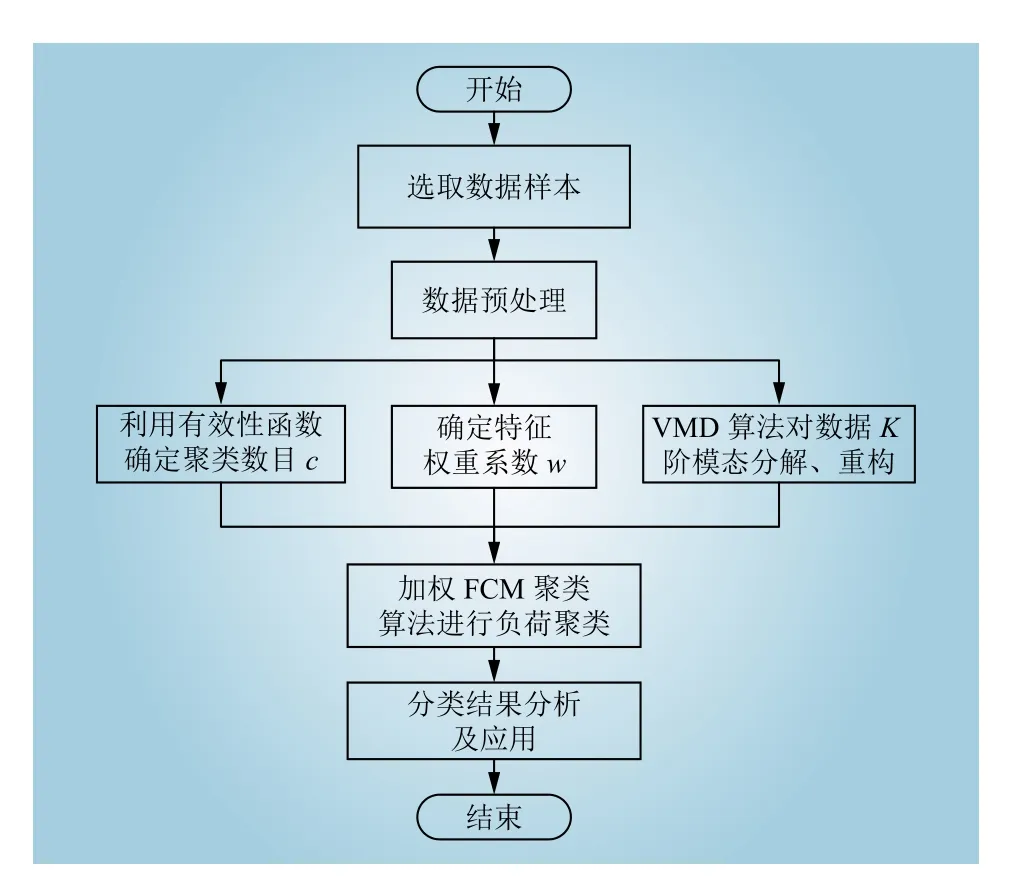
图1 加权VMD-FCM算法负荷分类流程Fig. 1 Flow chart of load classification with weighted VMD-FCM algorithm

其中，样本数据为在工作日时间内选取的一定容量的负荷数据，并作为VMD算法的待解析信号组。由于电网采集系统采集到的数据结构比较粗糙，可能具有坏点、断点等，需要对不良数据进行修正、标准化和无量纲化等预处理。通过标准数据集，选定加权可能性划分系数P'(U,c)，并利用其确定聚类数目c，与VMD算法解析重构后的数据组成参数组输入到加权FCM算法中，最终得到分类结果并进行分析。负荷分类最终在于挖掘每个用户的负荷特性，并作为电网进行相关决策的指导。

3 仿真实验及结果分析

3.1 案例分析

本案例负荷数据来自我国南方某地区电网供电公司数据采集与监视控制系统（supervisory control and data acquisition，SCADA），根据帕累托二八定律[20]，即20%的用电用户所消耗的用电量可占据全部用户用电总量的80%，因此大用户群体在负荷管理中表现出主导地位。本文选取的大用户以工业用户为主，主要包括金属冶炼、矿物加工、化学化工等领域。选取20个大电力用户的7月份工作日负荷数据进行实验分析，其中采样时间为以24 h为周期，每15 min采样一次，即96点日负荷曲线图。对用户的日负荷数据作平均值处理，得到20个大用户的典型日负荷数据曲线。虽同为大用户群体，但各用户负荷差异显著，为比对不同负荷曲线，对20组典型日负荷曲线进行归一化预处理，使之全部位于0到1之间。归一化数据表达式为

随机选取一条典型日负荷数据曲线，利用VMD算法分别对曲线进行3、4、5阶模态的分解与重构。重构后的曲线特性如图2所示，基于维纳滤波器良好的鲁棒性，在进行VMD重构后的曲线可明显去除原数据的噪声，维持负荷曲线的连贯性及原有特性，并且从图中可以看出与原曲线相比具有良好的相似度。

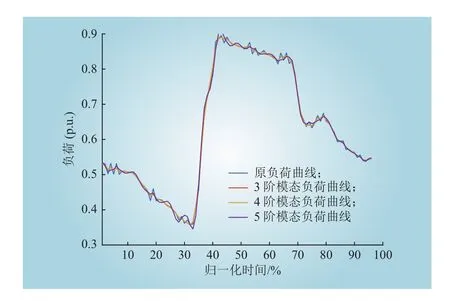
图2 原曲线及重构曲线Fig. 2 Original curve and reconstruction curve

3.2 聚类算法应用

3.2.1 聚类数目研究

在实际数据分类数未知的情况下，首先需要利用内部有效性函数对聚类数目c进行确定。首先研究Xie-Beni指标XBI[21]、可能性划分系数指标FP(U,c)[22]、模糊熵函数E(U,c)[23]、加权可能性划分系数P'(U,c)[24]对聚类数目的影响，选取与负荷曲线特征数目更加接近及分类数目较为适中的glass数据集进行验证分析。glass数据集由214个样本组成，特征数为9，分类数为6，每类样本数目分别为70、76、17、13、9、29。聚类结果如表1所示。

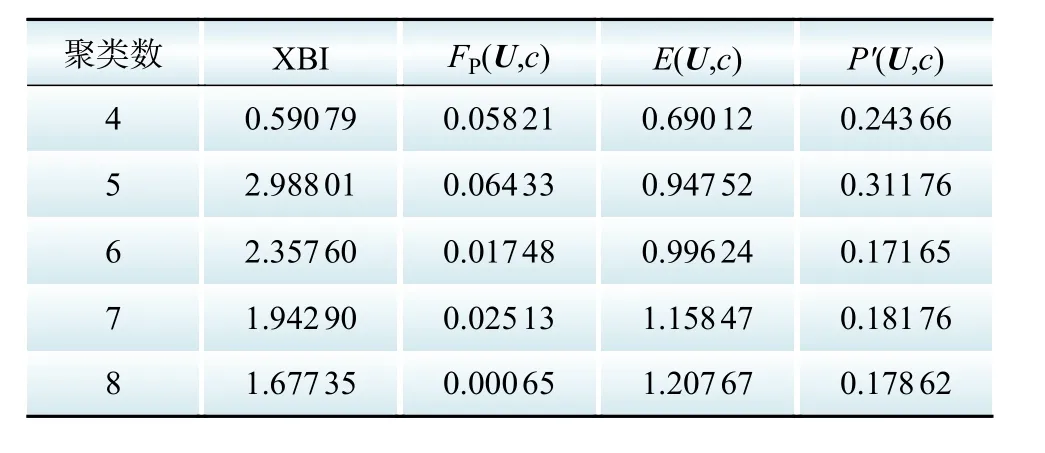
表1 glass数据聚类结果Table 1 Glass data clustering results

对上述具有较好分离性的数据集来说，上述指标大致都能反映出最优聚类数目。针对glass数据集，P'(U,c)指标在聚类数为6时，其值为0.171 65，为P'(U,c)指标在所有聚类数中的最小值，满足式（14）的指标定义式，在4个指标中最为准确。该指标突出了数据的类内紧凑性及类间分离性，并且将数据的模糊划分与几何结构相融合，可用于负荷分类研究。P'(U,c)指标定义公式为

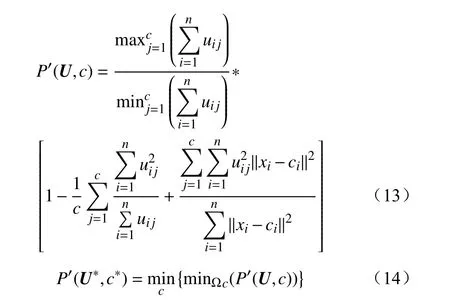
式中：ci为第i个聚类中心。满足式（14）的c*即为最佳的聚类结果[25]。

3.2.2 实例聚类分析

利用P'(U,c)指标对20个电力用户进行聚类分析，根据FCM算法中求取P'(U,c)指标的最小值来获得最佳的聚类数目c。选取FCM聚类数目c为3 ～8，隶属度矩阵U指数m=2，权重系数ω取为96点权重都为1，选取VMD算法预设K值为3、4、5，利用原负荷曲线及VMD分解重构的3组负荷曲线进行聚类结果分析，算法聚类的P'(U,c)指标结果如表2所示。

由表2中FCM算法的聚类结果可以看出，当聚类数目c=3时，P'(U,c)指标达到最优值。比较FCM算法及VMD-FCM算法的结果可知，经过VMD分解后重构的负荷曲线更适合FCM算法聚类，当预设模态K=3时，聚类效果最佳，并且随着聚类数目c的增加，指标特性分离程度更加明显。由此表明VMD-FCM算法聚类结果优于FCM聚类算法，提高了聚类的准确性。由图3能够看出，将原始数据带入FCM聚类算法中，其迭代次数为20，经过3 ～5阶模态分解重构后的曲线迭代次数分别为8、16、17，且经VMD重构后的实验数据其目标函数值略低于原始数据。图4、图5为聚类数目c=3时，FCM算法及K=3时VMD-FCM算法的聚类结果，实验表明VMD重构曲线能明显加快FCM聚类算法的收敛速度，且能够提升聚类的类间紧凑性及分离性，在维持负荷曲线原有特性基础上，提高其平滑度，降低噪声干扰。

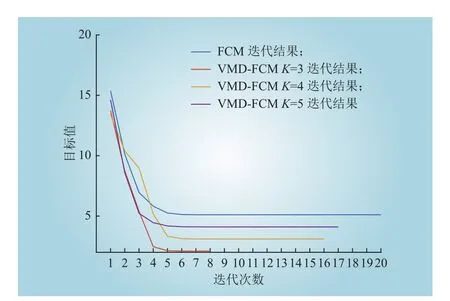
图3 FCM及VMD-FCM迭代结果Fig. 3 FCM and VMD-FCM iteration results

图4 FCM算法聚类结果Fig. 4 FCM algorithm clustering results

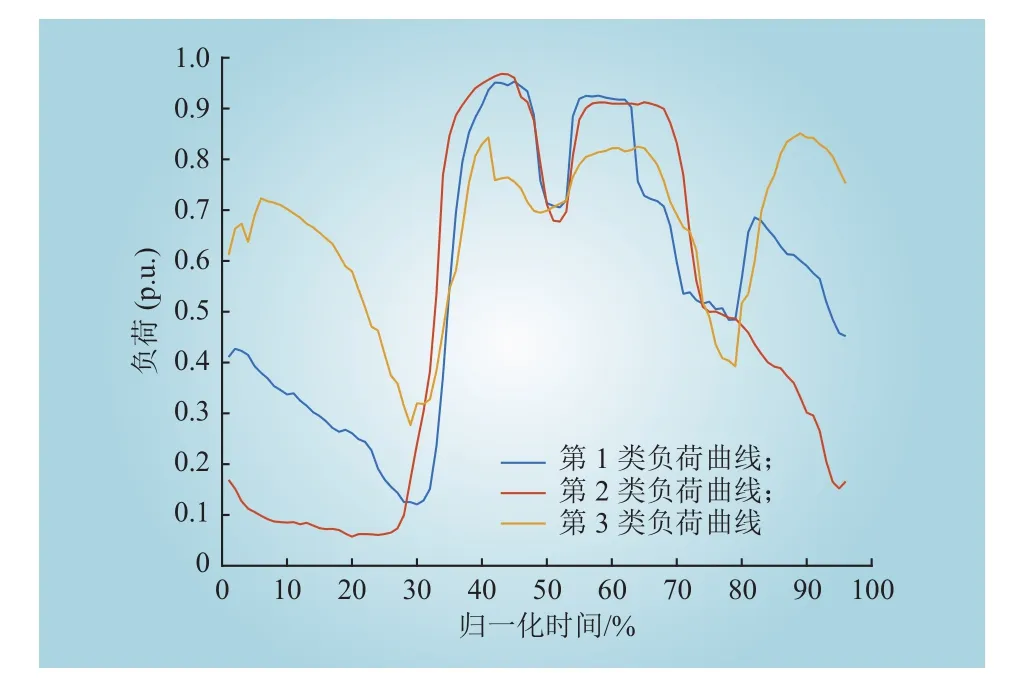
图5 基于3阶模态分解的VMD-FCM算法聚类结果Fig. 5 Clustering results of VMD-FCM algorithm based on third-order mode decomposition

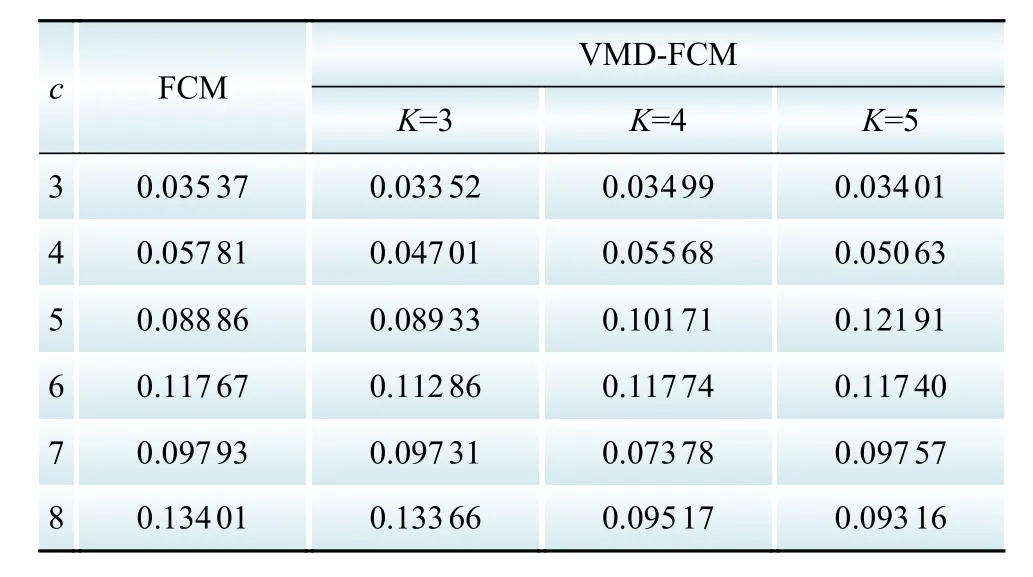
表2 P'(U,c)指标聚类结果Table 2 P'(U,c) index clustering results

3.2.3 加权系数研究

用户典型日负荷曲线在聚类分析时，构成样本集的特征矢量各维特征代表不同时刻的实际意义，因此存在聚类精度及实用性不强等弊端，为解决实用性低的问题，将一个单位周期内所有的特征矢量赋予一定的特征权重，以此更加接近实际应用效果，实现负荷分类的物理意义。

本文将特征权重系数w={w1,w2,…,wk}引入到欧式距离上，形成加权欧氏距离，从而控制各维特征矢量的权值与实际地区供电方案一致。首先设定三组特征权重，比较不同权重下的FCM目标函数Jm值及P'(U,c)指标的变化情况。设定wi=1(i=0,1,2,3,4,5,6,7,20,21,22,23)，wi分别取 2、3、4(i=8,9,…,19)，即取一天中用电量高峰时段（08:00—19:00）的权重系数w为2、3、4，其余时段的权重系数w为1。当权重系数w都为平均权重1时，即为未加权重系数的FCM聚类。如表3所示，记录了不同特征权重系数下的FCM目标函数Jm及P'(U,c)指标，表4为08:00—19:00时段w=3的P'(U,c)指标值，图6为加入权重系数后最优分类数为5的20个样本VMD-FCM聚类结果，每类分别包含的样本数为4、4、4、5、3个。

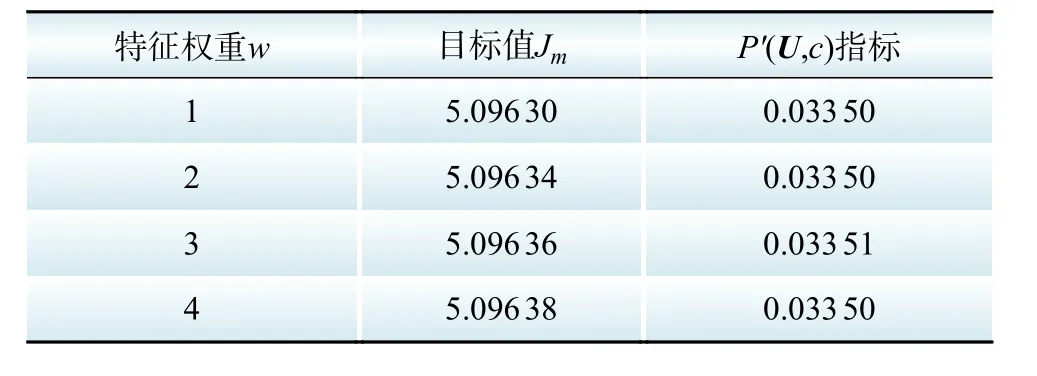
表3 时段08:00—19:00不同特征权重下的Jm及P'(U,c)Table 3 Jm and P'(U,c) under different feature weights in the period of 08:00—19:00

表4 时段08:00—19:00w=3的P'(U,c)指标值Table 4 The index value of P'(U,c) with w=3 in the period of 08:00—19:00

图6 基于三阶模态分解的加权VMD-FCM聚类结果Fig. 6 Weighted VMD-FCM clustering results based on third-order mode decomposition

由表3及表4结果可以看出，FCM算法加入特征权重w后，其聚类中心并没有改变，但隶属度矩阵U及目标函数Jm会受到影响，划分系数P'(U,c)指标没有发生大的变化。由表4能够看出当聚类数目为5时，P'(U,c)指标能够达到最优值，表明加入权重系数后的最优分类数目会受到影响。5类负荷用户在黑色虚线内，即时段08:00—19:00负荷处于高位，在08:00、19:00时附近负荷有骤降趋势，说明这两时间段内用户用电相对较少。在针对电网用电规划方面，可适当提高白天08:00—19:00时的w值，适当降低时段06:00—09:00、19:00—21:00的w值，合理配置电力系统用电规律，为电网减负降耗。

特征权重w的加入，一定程度上改变了欧式距离的实际意义，从而将每个样本各个特征分量进行加权处理，使得典型负荷曲线不再是单一权值的曲线，而是与地区电网供电方案的有效结合，根据供电实际需要，确定相应的权重系数，对样本进行聚类分析，形成科学准确的负荷分类结果。